2023年的深度学习入门指南(17) - 深度学习的硬件加速技术
有了前面的知识之后,想必大家对于算力需求的理解已经越来越深刻了。
除了使用CPU,GPU这样的通用器件之外,采用专用的硬件来进行加速是一个大家都能想到的选择。
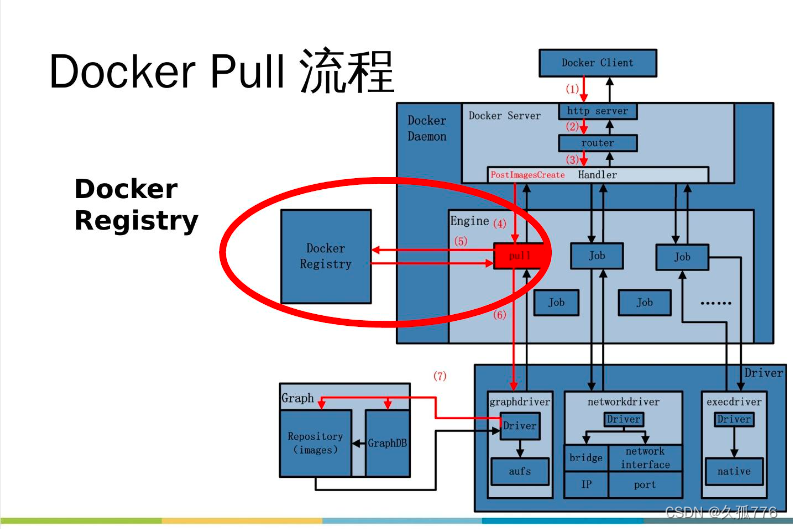
其中的代表器件就是我们上一节刚刚用到的TPU。下图是TPU的样子及其结构图:
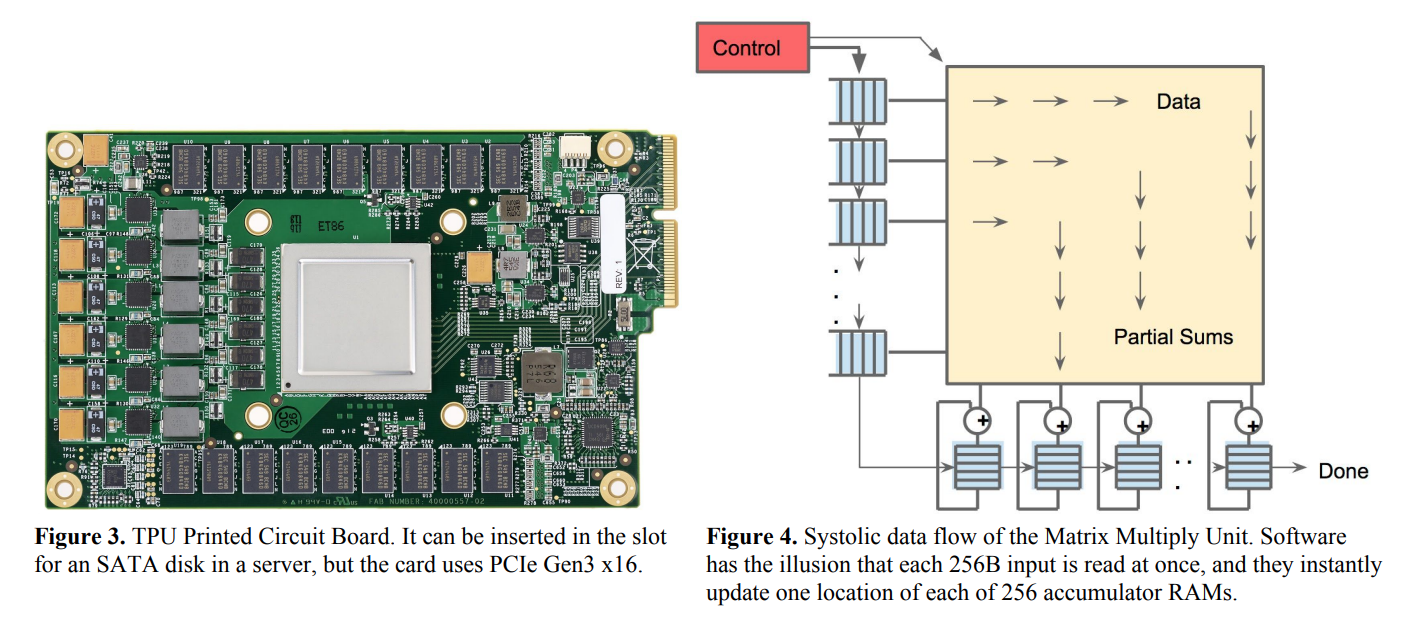
那么,TPU为什么设计成以矩阵乘法为核心呢?我们先从深度学习的原理开始了解一下。
神经网络和注意力的计算方法
人工神经网络的基本计算单元是神经元。每个神经元的结构如下图所示:
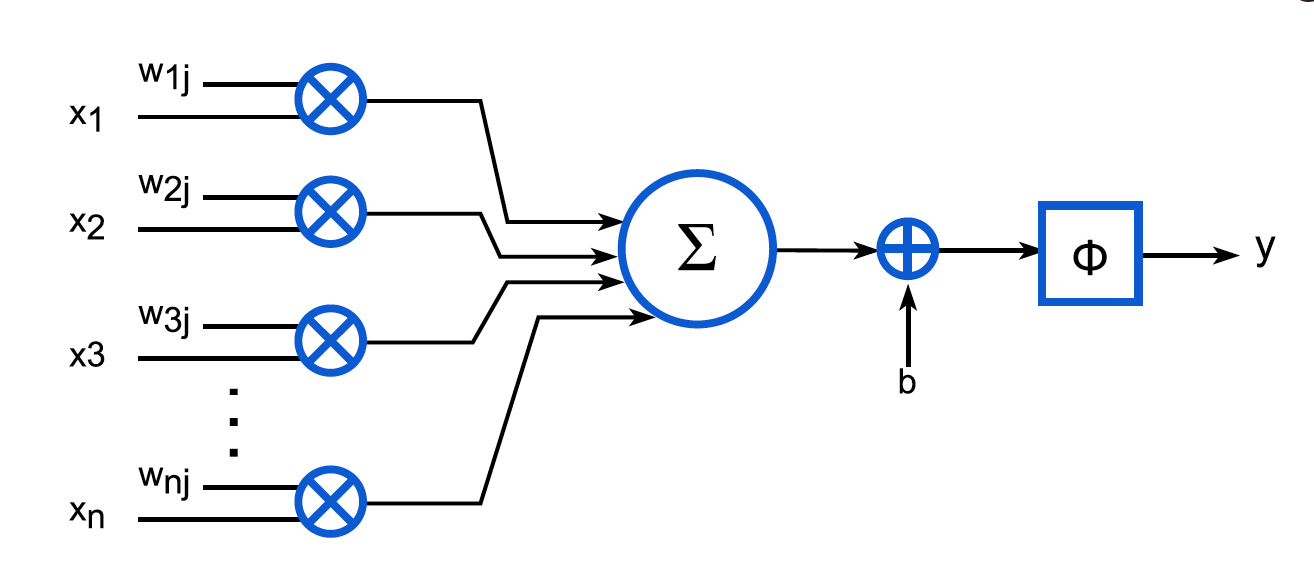
用公式来表示就是:
y j = Φ ( ∑ k = 0 n − 1 x k w k j + b ) y_j=\Phi\left(\sum_{k=0}^{n-1} x_k w_{k j}+b\right) yj=Φ(∑k=0n−1xkwkj+b)
其中,
x
k
x_k
xk是输入,
w
k
j
w_{k j}
wkj是权重,
b
b
b是偏置,
Φ
\Phi
Φ是激活函数,
y
j
y_j
yj是输出。
我们可以看到,每个神经元的计算都是一个矩阵乘法加上一个偏置,再经过一个激活函数。
我们再复习一下之前讲多头自注意力模型的结构图:

我们可以看到,主要的计算仍然是矩阵乘法和加法。
Q u e r y : Q i = X ∗ W i Q Query: Q_i = X * W_i^{Q} Query:Qi=X∗WiQ
K e y : K i = X ∗ W i K Key: K_i = X * W_i^{K} Key:Ki=X∗WiK
V a l u e : V i = X ∗ W i V Value: V_i = X * W_i^{V} Value:Vi=X∗WiV
注意力权重 : A i = s o f t m a x ( Q i ∗ K i T / s q r t ( d k ) ) 注意力权重: A_i = softmax(Q_i * K_i^T / sqrt(d_k)) 注意力权重:Ai=softmax(Qi∗KiT/sqrt(dk))
输出 : O i = A i ∗ V i 输出: O_i = A_i * V_i 输出:Oi=Ai∗Vi
有了上面的基础,我们来看一下TPU的结构图:
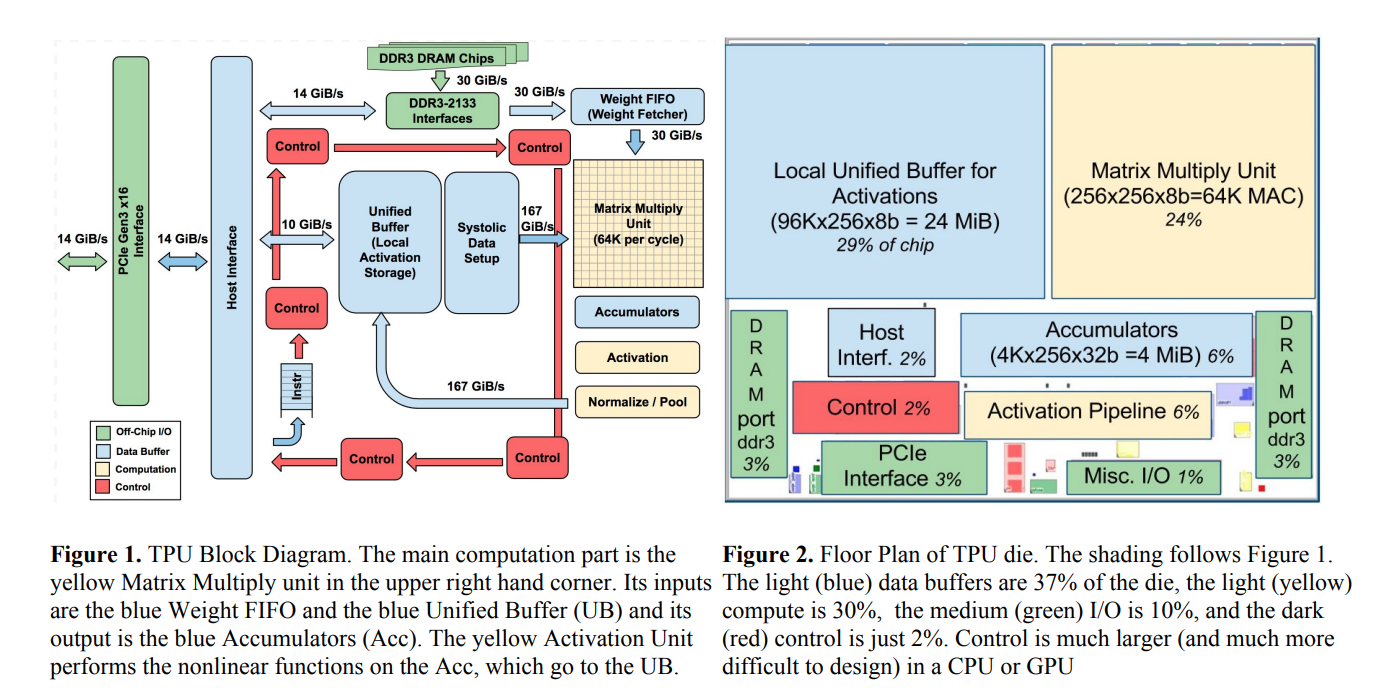
可以看到右上角占四分之一空间的矩阵乘法单元,与左上部的本地缓存,构成了TPU的最主要部分。
上图中的MAC是Multiply-and-accumulate的缩写,表示乘法加上累加运算。也就是说在最初的TPU上,每个指令周期可以进行64K次乘法和加法运算。
硬件近似方法
矩阵乘法是一个非常耗时的运算,而且在深度学习中,我们并不需要非常精确的结果。因此,我们可以采用一些近似的方法来加速矩阵乘法的运算。
与我们之前学习的量化和剪枝的方法类似,在硬件方法上我们也可以使用量化和计算简化的方法。除此之外,在硬件设计上我们还可以采用近似计算单元来代替精确计的计算器件。

近似计算单元主要有三种方式,首先是采用近似的加法乘法器,其次是通过使用对数的方式将乘法转化为加法运算,最后是干脆去掉乘法器。
前面我们对量化已经有比较详细的介绍了,这里就不再赘述了。我们重要介绍下后面两种方法,也就是计算简化和近似计算单元。
计算简化 - 跳过
计算简化的第一种方法就是跳过不算。

在大模型中,由于数据量很大,其实有很多数据是0,或者是非常接近0的。这些数据对于最终的结果影响非常小,因此我们可以直接跳过这些数据的计算。
我们就可以设计下面这样跳过接近0的数据的计算单元:
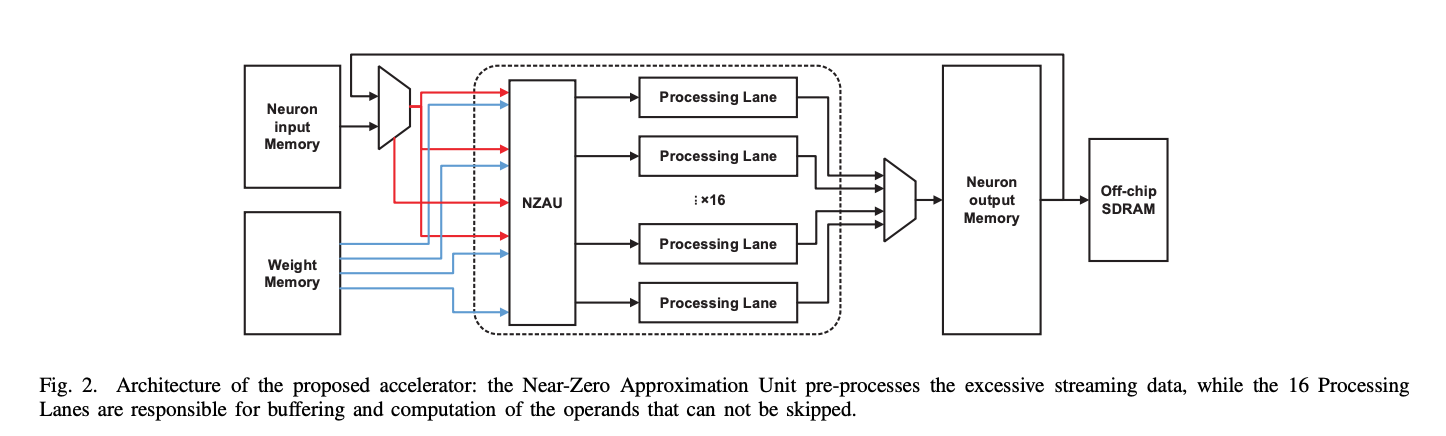
计算简化 - 记忆
计算简化的第二种方法就是记忆,也就是说我们可以将之前的计算结果保存下来,下次再用到的时候直接使用。这不就是动态规划的思想吗?这种方法的效率取决于输入的相似性(即替换发生的频率)以及被消除的计算的复杂度。
输入的相似性越高,被消除的计算的复杂度越高,这种方法的效率就越高。
比如,论文《(Pen-) Ultimate DNN Pruning》提出了一种两步的修剪方法,首先通过对每层的输出进行PCA分析来移除冗余节点,然后通过考虑其相对于给定神经元的其他连接的贡献来移除剩余的不重要连接。
近似计算单元 - 近似乘法加法器
在近似电路的实现中,一个比较有效的方法是笛卡尔遗传编程GCP方法。最基本的实现如下所示:

Cartesian Genetic Programming (CGP) 是一种遗传编程的形式,它使用图形表示法来编码计算机程序。它起源于Julian F. Miller和Peter Thomson在1997年开发的一种演化数字电路的方法,它被称为“笛卡尔”因为它使用二维网格的节点来表示一个程序
遗传编程是一种启发式搜索技术,用于优化或发现可以执行用户定义任务的计算机程序。基本的遗传编程系统使用遗传算法,这是一种根据生物进化的原理(包括遗传、变异、自然选择和重组)运行的搜索算法。
在笛卡尔遗传编程中,程序是由图表表示的,图表由节点组成,每个节点代表一个函数或操作。这些节点在二维网格中排列,形成一种计算流,这是计算从输入节点流向输出节点的路径。通过这种方式,CGP能够演变出能够完成特定任务的复杂程序。
笛卡尔遗传编程生成的乘法器满足给定的最坏情况误差约束,并确保对0的乘法始终准确无误。它采用迭代优化过程来确定CGP优化中的近似乘法器生成的误差约束,以满足推断准确性损失的阈值。并且,在迭代过程中,将准确的乘法器替换为近似乘法器后,对网络进行重新训练以获得最佳质量结果。
以应用GCP的基础论文《Design of power-efficient approximate multipliers for approximate artificial neural networks.》为始,后面有一系列的改进,比如使用weighted mean error distance (WMED)来进行误差度量。计算WMED时,每个误差的重要性由网络权重分布的概率质量函数确定。
论文《Neural Networks with Few Multiplications》提出了一种两步的方法:首先,作者通过随机二值化权重,将计算隐藏状态所需的乘法操作转化为符号更改。其次,在反向传播误差导数的过程中,除了二值化权重,作者还对每一层的表示进行量化,将剩余的乘法操作转换为二进制位移。
另外,再使用了三值连接(Ternary Connect)、量化反向传播(Quantized Backprop)和批量归一化(Batch Normalization)后,误差率可以降至1.15%,这比全精度训练的误差率1.33%要低。这表明,即使去除了大部分乘法,这种方法的性能仍然可以与全精度训练相媲美,甚至略有提高。性能的提高可能是由于随机采样所带来的正则化效应。
论文《ALWANN:Automatic layer-wise approximation of deep neural network accelerators without retraining》提出的方法包括两个部分:第一部分是将一个完全训练好的DNN转换为在卷积层中使用8位权重和8位乘法器的操作;第二部分是从一个近似乘法器的库中为每个计算单元选择一个合适的近似乘法器,使得(i)一个近似乘法器可以服务于多个层,(ii)整体的分类误差和能耗最小化。
下图是寒武纪的DaDianNao芯片计算近似乘法的架构图。
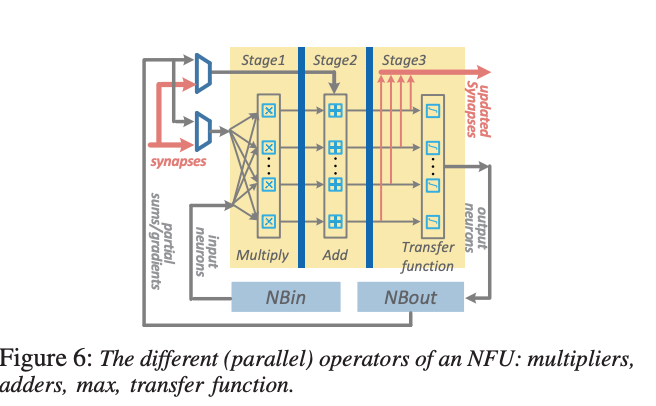
论文《Design automation of approximate circuits with runtime reconfigurable accuracy》提出了一种自动的设计框架,可以生成具有运行时可重配置精度的近似电路。论文的方法包括两个部分:第一部分是使用遗传算法对给定的电路进行门级近似,从而在不影响功能正确性的前提下,减少电路的开销;第二部分是在近似电路中添加可重配置单元,使得电路可以在运行时根据应用需求和环境条件,切换不同的精度级别。
近似计算单元 - 无乘法器设计
看过了专用硬件TPU,DaDianNao,我们来看一种新的器件FPGA。
论文《AddNet: Deep Neural Networks Using FPGA-Optimized Multipliers》
提出了一种使用FPGA优化的乘法器来实现深度神经网络的方法,称为AddNet。该方法利用了可重配置的常数系数乘法器(RCCM),它们可以用加法器、减法器、位移和多路复用器(MUX)来实现乘法运算,从而在FPGA上进行高度优化。作者设计了一系列适合FPGA逻辑元件的RCCM,以保证它们的高效利用。为了减少量化造成的信息损失,作者还开发了一种新颖的训练技术,将RCCM的可能系数表示映射到神经网络权重参数分布上。这使得在硬件上使用RCCM时,仍能保持高精度。

类似地,论文《Energyefficient neural computing with approximate multipliers》这篇文章的主要观点是提出了一种使用近似乘法器来实现能量高效的神经计算的方法。该方法利用了神经网络应用的错误恢复能力,使用计算共享的概念来实现低精度的乘法运算,从而节省硅面积或提高吞吐量。作者设计了一种近似乘法器,它使用加法器、减法器、位移和多路复用器(MUX)来实现乘法运算,从而在FPGA上进行高度优化。通过用简化的移位和加法操作替换乘法器,并由一个单元控制,使用无乘法器的神经元。所谓的字母集乘法器(ASMs)由预计算器库组成,根据一些称为字母表({1, 2, 3, 5, . . .})的小位序列,一个加法器,以及一个或多个选择、移位和控制逻辑单元来计算输入的低阶倍数。字母表的大小定义了ASM的准确性和能量收益。最后进行有效的重新训练,以调整权重并减轻由于ASMs引起的准确性下降。

近似计算单元 - 近似对数乘法器
通过使用对数和指数来将乘法运算变成加法运算的研究由来已久了,John N. Mitchell在1962年的论文"Computer multiplication and division using binary logarithms"中提出了一种使用二进制对数进行计算机乘法和除法的方法。该方法通过简单的移位和计数,可以从二进制数本身大致确定其对数。只需要一个简单的加法或减法和移位操作,就可以完成乘法或除法。
下面是一种改进的算法的示意图,涉及到的公式较多,就不细讲了:
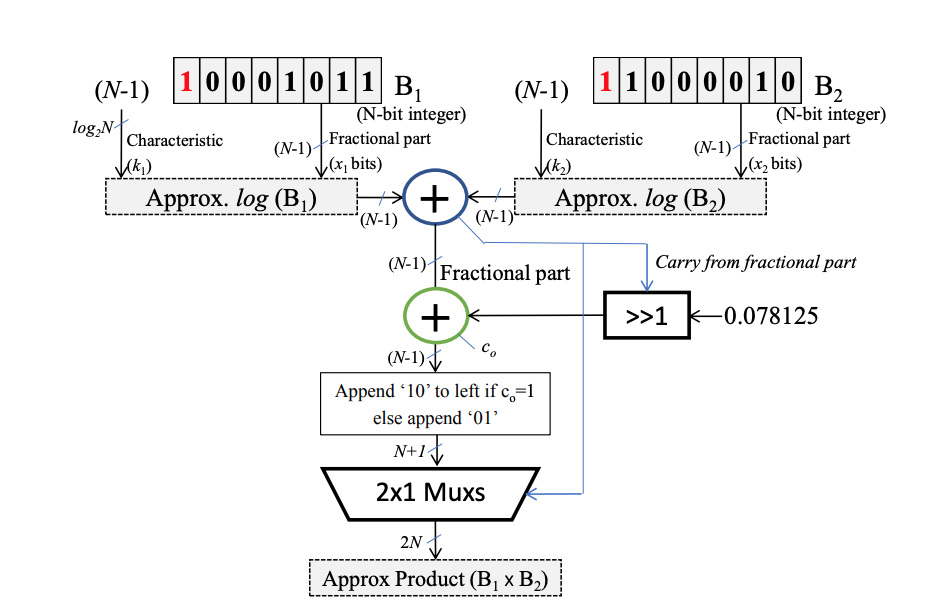
小结
这一节只想给大家普及一点,就是因为神经网络的宽容性,给各种硬件优化带来了不小的空间。虽然目前大模型的训练基本只能使用NVidia GPU,但是未来的训练和推理一定还有很多可以优化的空间。
请大家随时关注硬件的发展情况,如果发现可以用于自己业务场景的硬件可以节省成本或者推升性能,一定保持开放心态去尝试一下。