第一章 基础算法（一）—— 快排，归并与二分

news2024/11/23 10:40:07

文章目录

    • 快排
    • 归并排序
    • 二分
      • 整数二分
      • 浮点数二分
    • 快速排序练习题
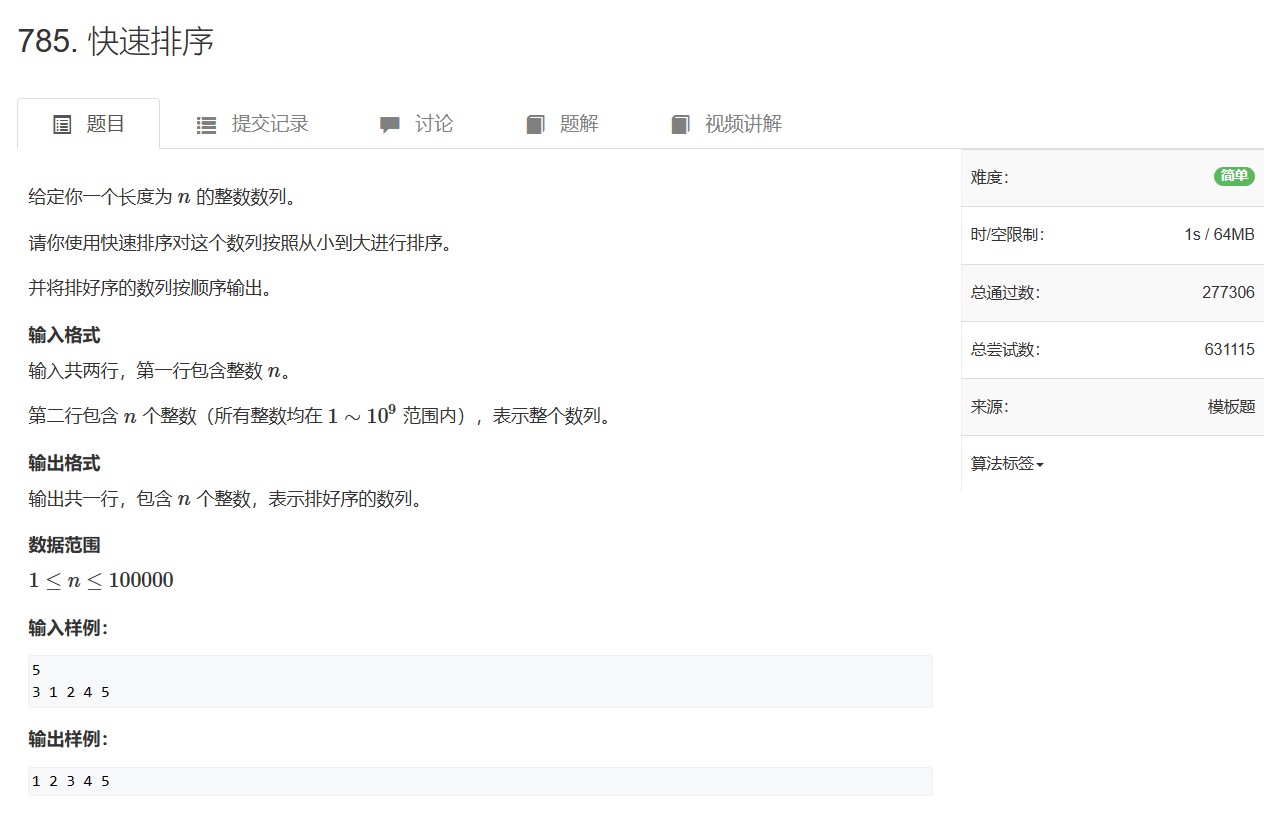
      • 785. 快速排序
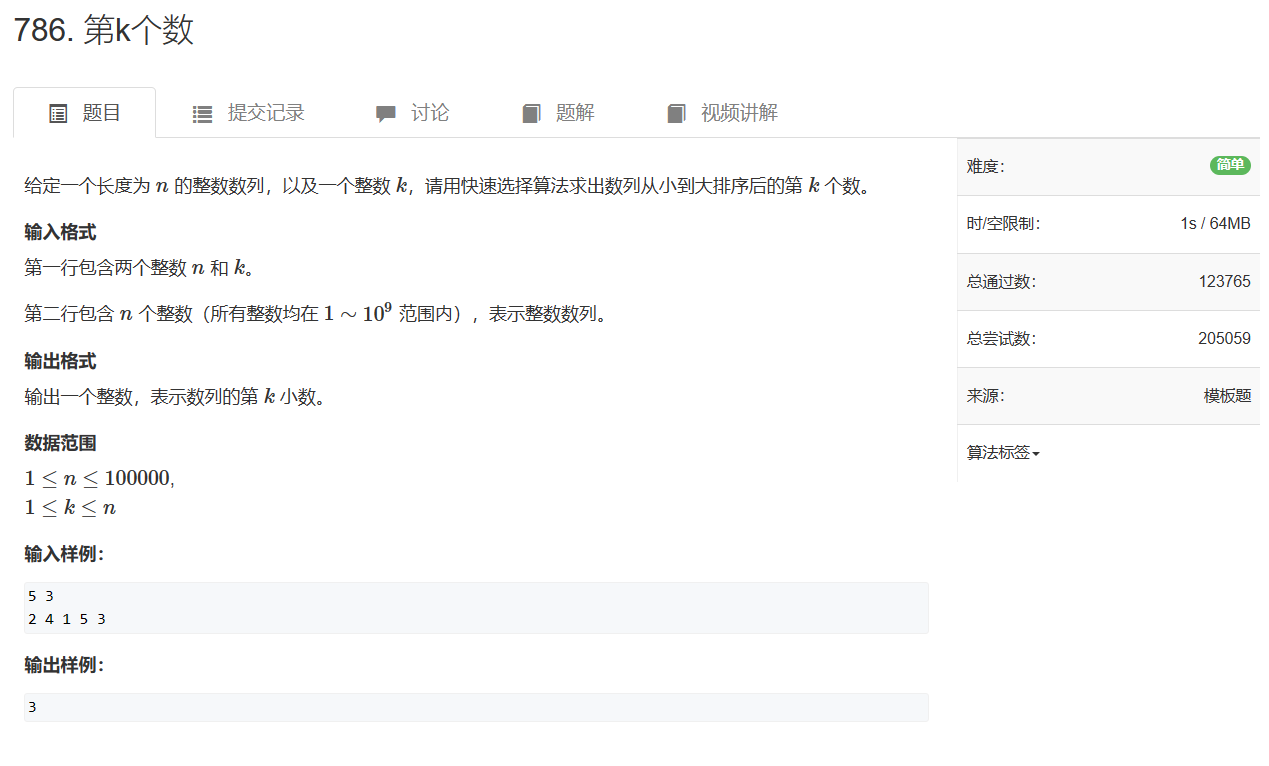
      • 786. 第k个数
    • 归并排序练习题
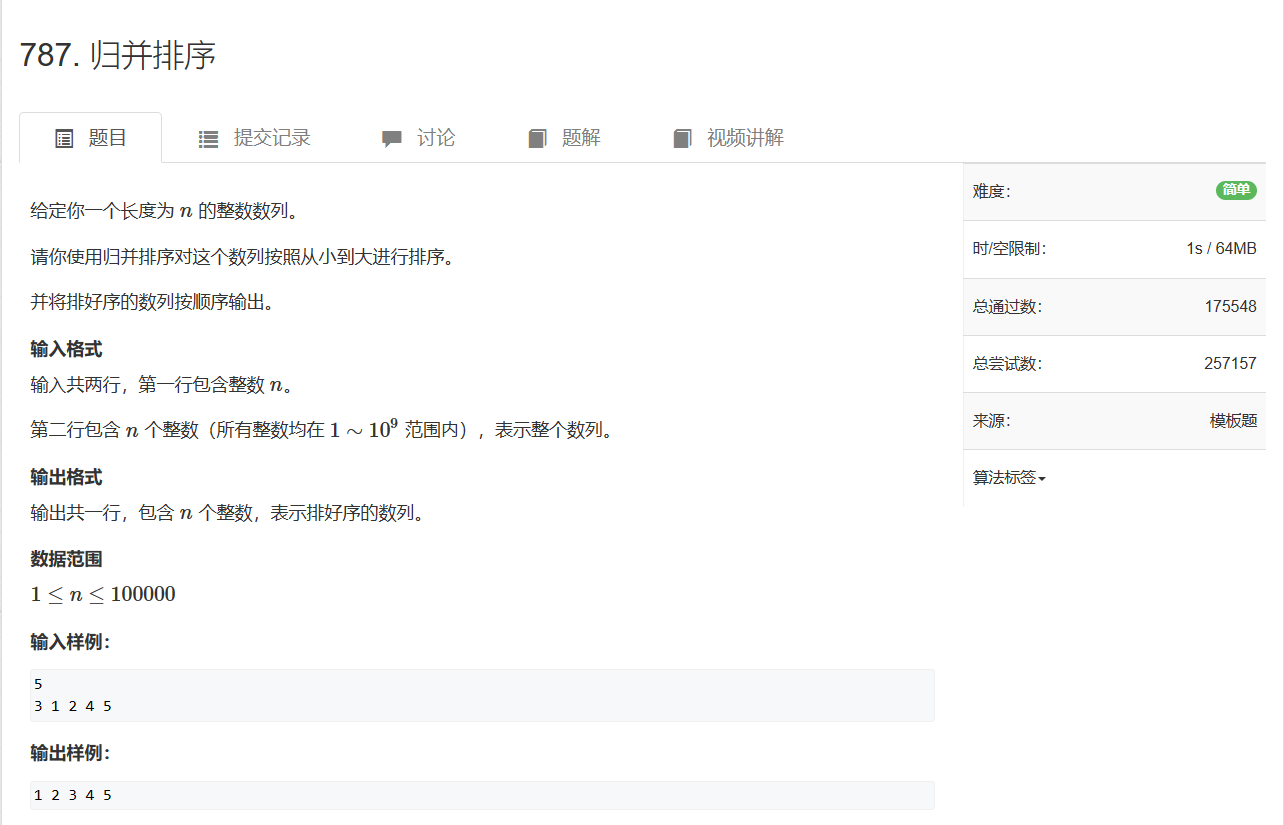
      • 787. 归并排序
      • 788. 逆序对的数量
    • 二分练习题
      • 789. 数的范围
      • 790. 数的三次方根

有些累了，把这两天做的笔记整理发出

快排

快排的思路：

  1. 确定分界点
  2. 根据分界点，调整区间中的数
  3. 递归左右区间

其中第2点是快排的关键，采用双指针法。

  1. i从0开始往右走，j从n - 1开始往左走
  2. 若nums[i] > x，i停下，否则继续往右走
  3. 若nums[j] < x，j停下，否则继续往左走
  4. 当两个指针都停下，交换两指针指向的数，接着重复2，3步，直到i与j相遇

当两个指针都停下时，
i左边的所有数小于x，i的右边以及i的位置上所有的数大于等于x
同理j右边的所有数大于x，j的左边以及j的位置上所有的数小于等于x
此时可以选择i或者j分割nums数组，分割后的数组为[l, j]和[j + 1, r]，

快排模板：

void quick_sort(int nums[], int l, int r)
{
	if (l >= r) return;
	int x = nums[(l + r) >> 1], i = l - 1, j = r + 1;
	while (i < j)
	{
		do ++i; while (nums[i] < x);
		do --j; while (nums[j] > x);
		if (i < j) swap(nums[i], nums[j]);
	}
	quick_sort(nums, l, j);
	quick_sort(nums, j + 1, r);
}

需要注意选择分界点时，必须选择(l + r) / 2 ，不能除3，不能除4
以及递归子区间时，不能选择i作为分界点，因为会导致死循环

关于死循环的例子：1, 2
当区间划分为[l, j]和[j + 1, r]时，x = mid[r]会出现死循环问题
当区间划分为[l, i - 1]和[i, r]时，x = mid[l]会出现死循环问题

归并排序

归并排序的思路：

  1. 确定分界点：mid = (l + r) / 2
  2. 递归排序左右两个子区间
  3. 归并区间，合二为一

其中最重要的是第三步，涉及到两个有序区间的合并

合并两个有序区间的算法：双指针

  • 用两个指针指向数组中的开始位置
  • 将较小的数放入tmp数组中，并向后移动该指针
  • 直到有一个指针遍历完一个数组，此时将未遍历完的数组直接拼接到tmp数组中
  • 最后将tmp数组中的数，拷贝回nums数组

归并模板：

const int N = 1e6 + 10;
int nums[N], tmp[N};
				 
void merge_sort(int nums[], int l, int r)
{
    if (l >= r) return;
    int mid = l + r >> 1;
    
    merge_sort(nums, l, mid), merge_sort(nums, mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
    {
        if (nums[i] <= nums[j]) tmp[k++] = nums[i++];
        else tmp[k++] = nums[j++];
    }
    
    while (i <= mid) tmp[k++] = nums[i++];
    while (j <= r) tmp[k++] = nums[j++];
    for (i = l, k = 0; i <= r; ++i, ++k) nums[i] = tmp[k];
}

快排和归并的时间复杂度都是nlogn，在最坏的情况下，快排可能达到n * n。而归并总是nlogn

二分

整数二分

二分的本质不是单调性，有单调性的题目一定可以二分，但是可以二分的题目不一定具有单调性

二分的本质是边界。确定一个性质，使左右区间中其中一个区间满足该性质，另一个区间不满足该性质

因此，找到一个性质，左右区间的边界点就可以二分出来。
image.png

红绿区间的交界处，其中一个交界就是要查找的数x的位置。
举个例子，整个数组为nums，左边区间中的数满足nums[k] <= x的性质，右边区间中的数满足nums[k] > x的性质，此时左边区间的边界就是要查找的x的位置。

对于mid的计算：mid = (l + r) / 2，有时mid = (l + r + 1) / 2

check函数连接了nums数组中的数与要查找的数x，它是一个关于x的性质。

check函数的更新：
当check函数检查的是：mid是否满足左边区间的性质时

  • if (check(mid))
    • true： mid落在左边区间中，要查找的数落在[mid, r]中，更新l = mid
    • false：mid落在右边区间中，要查找的数落在[l, mid - 1]中，更新r = mid - 1
      当check函数检查的是：mid是否满足右边区间的性质时
  • if (check(mid))
    • true： mid落在右边区间中，要查找的数落在[l, mid]中，更新r = mid
    • flase：mid落在左边区间中，要查找的数落在[mid + 1, r]中，更新l = mid + 1

需要注意的是：对于check，若mid满足某个区间的性质，可能mid就是要查找的x。因此区间更新时不应该舍弃mid

二分的两个模板：

// 检查左边区间是否满足性质时使用
// 也就是区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用
int bsearch_1(int l, int r)
{
	if (l >= r) return;
	while (l < r)
	{
		int mid = (l + r + 1) >> 1;
		if (check(mid)) l = mid;
		else r = mid - 1;
	}
	return l;
}

// 检查右边区间是否满足性质时使用
// 也就是区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用
int bsearch_2(int l, int r)
{
	if (l >= r) return;
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (check(mid)) r = mid;
		else l = mid + 1;
	}
	return l;
}

当更新方式是r = mid时，mid = (l + r) >> 1
当更新方式是l = mid时，mid = (l + r + 1) >> 1
为什么此时的mid要加1？当l = r - 1时，变形一下：r = l + 1
由于语言是向0取整的，若不加1，此时mid = (2 * l + 1) = l
若check为true，更新l = mid = l，l作为区间的左端点，没有变化。而区间的右端点r也没有变化，此时区间没有更新，将陷入死循环

思路：

  1. 思考check函数（性质）
  2. 根据check函数思考区间如何更新
  3. 根据区间的更新方式，决定mid是否要+1

二分一定有解，但题目可能无解。根据二分出来的答案，判断答案是否满足题目要求，进而判断题目是否有解

浮点数二分

浮点数二分没有边界问题，所以不会存在死循环的情况，也就不需要思考是否要+1-1
简化整数二分的模板即可：

// 假设题目要求保留6位小数
int bsearch_3(int l, int r)
{
	if (l >= r) return;
	while (r - l > 1e-8)
	{
		int mid = (l + r) / 2;
		if (check(mid)) l = mid;
		else r = mid;
	}
	return l;
}

check函数中：检查区间的不同，l和r的更新也不同。例如，以下是将x开方的两种写法

#include <iostream>
using namespace std;

int main()
{
    double x = 0;
    cin >> x;
    double l = 0, r = x;
    while (r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if (mid * mid <= x) l = mid;
        else r = mid;
    }
    printf("%lf", l);
    return 0;
}

#include <iostream>
using namespace std;

int main()
{
    double x = 0;
    cin >> x;
    double l = 0, r = max(1, x);
    while (r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if (mid * mid >= x) r = mid;
        else l = mid;
    }
    printf("%lf", l);
    return 0;
}

tips：若题目要求保留实数的n位小数，则二分的精度需要为n + 2，这样可以保证结果是准确的

浮点数二分还可以写for循环，循环100次，也就是将区间二分2的100次方次，此时得到的结果一定是准确的

#include <iostream>
using namespace std;

int main()
{
    double x = 0;
    cin >> x;
    double l = 0, r = x;
    for (int i = 0; i < 100; ++i)
    {
        double mid = (l + r) / 2;
        if (mid * mid <= x) l = mid;
        else r = mid;
    }
    printf("%lf", l);
    return 0;
}

快速排序练习题

785. 快速排序

785. 快速排序 - AcWing题库
image.png

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int nums[N];

void quick_sort(int nums[], int l, int r)
{
    if (l >= r) return;
    int x = nums[(l + r) / 2], i = l - 1, j = r + 1;
    while (i < j)
    {
        do ++i; while (nums[i] < x);
        do --j; while (nums[j] > x);
        if (i < j) swap(nums[i], nums[j]);
    }
    quick_sort(nums, l, j);
    quick_sort(nums, j + 1, r);
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    quick_sort(nums, 0, n - 1);
    
    for (int i = 0; i < n; ++i) printf("%d ", nums[i]);
    return 0;
}

需要注意选择分界点时，必须选择(l + r) / 2 ，不能除3，不能除4
以及递归子区间时，不能选择i作为分界点，因为会导致死循环

786. 第k个数

786. 第k个数 - AcWing题库
image.png
快排后，返回第k个数即可。

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int nums[N];
int n, k;

void quick_sort(int nums[], int l, int r)
{
    if (l >= r) return;
    int x = nums[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j)
    {
        do ++i; while (nums[i] < x);
        do --j; while (nums[j] > x);
        if (i < j) swap(nums[i], nums[j]);
    }
    quick_sort(nums, l, j), quick_sort(nums, j + 1, r);
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    quick_sort(nums, 0, n - 1);
    
    printf("%d\n", nums[k - 1]);
    return 0;
}

归并排序练习题

787. 归并排序

787. 归并排序 - AcWing题库
image.png

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int nums[N], tmp[N];
int n;

void merge_sort(int nums[], int l, int r)
{
    if (l >= r) return;
    int mid = l + r >> 1;
    
    merge_sort(nums, l, mid), merge_sort(nums, mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
    {
        if (nums[i] <= nums[j]) tmp[k++] = nums[i++];
        else tmp[k++] = nums[j++];
    }
    
    while (i <= mid) tmp[k++] = nums[i++];
    while (j <= r) tmp[k++] = nums[j++];
    for (i = l, k = 0; i <= r; ++i, ++k) nums[i] = tmp[k];
}

int main()
{   
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    merge_sort(nums, 0, n - 1);
    
    for (int i = 0; i < n; ++i) printf("%d ", nums[i]);
    
    return 0;
}

788. 逆序对的数量

788. 逆序对的数量 - AcWing题库
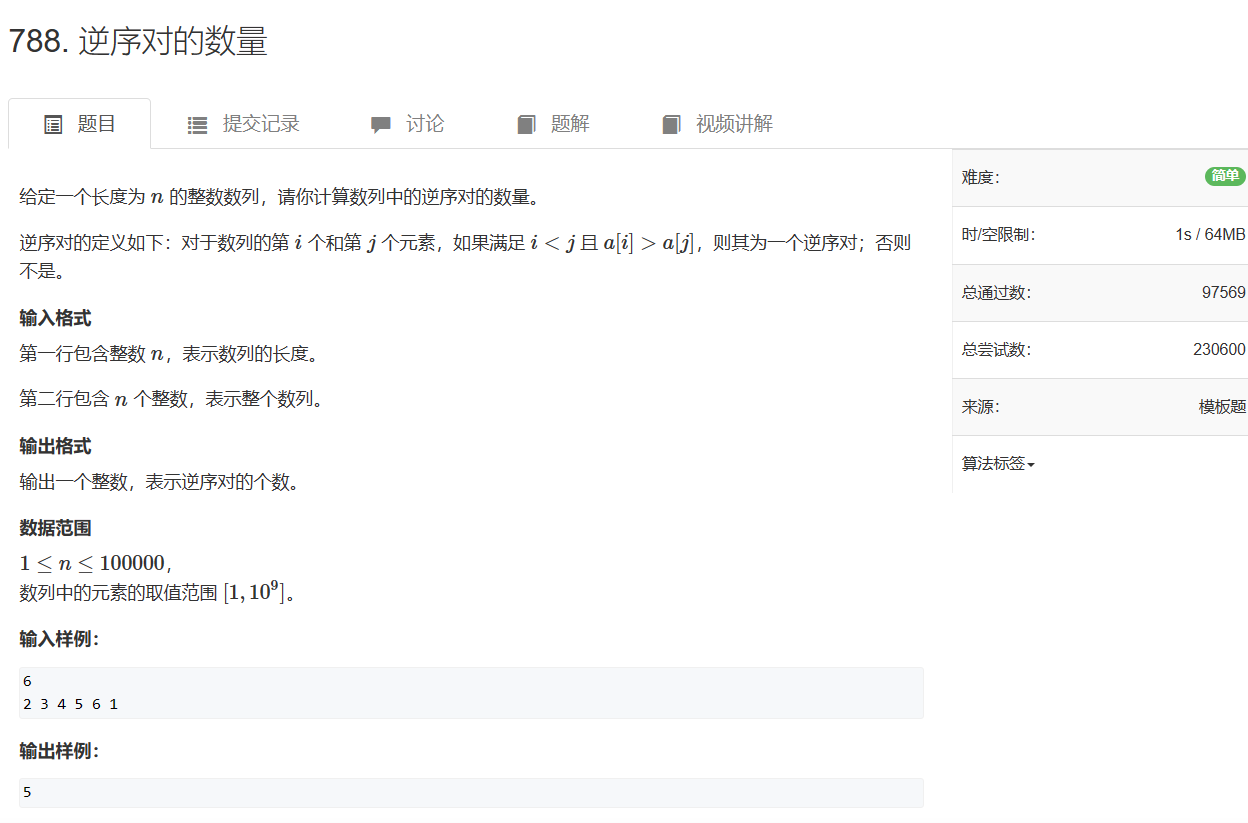
image.png
直接暴力搜索？直接超时了。
利用归并的性质，合并有序数组时，两个有序数组其实是两个左右区间，左区间的数字下标小于右区间的所有数字。当左区间中的某个数字nums[i]大于右区间的某个数字nums[j]时，说明该数字之后的所有数字都大于nums[j]。此时将包括nums[i]在内，向后的所有数字与nums[j]都能构成逆序对。将答案加上这个数，即mid - i + 1

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
typedef long long LL;
int n;
int nums[N], tmp[N];

LL merge_sort(int l, int r)
{
    if (l >= r) return 0;
    int mid = l + r >> 1;
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
    {
        if (nums[i] <= nums[j]) tmp[k++] = nums[i++];
        else 
        {
            tmp[k++] = nums[j++];
            res += mid - i + 1;
        }
    }
    while (i <= mid) tmp[k++] = nums[i++];
    while (j <= r) tmp[k++] = nums[j++];
    for (k = 0, i = l; i <= r; ++i, ++k) nums[i] = tmp[k];
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    printf("%ld\n", merge_sort(0, n - 1));
    
    return 0;
}

二分练习题

789. 数的范围

789. 数的范围 - AcWing题库
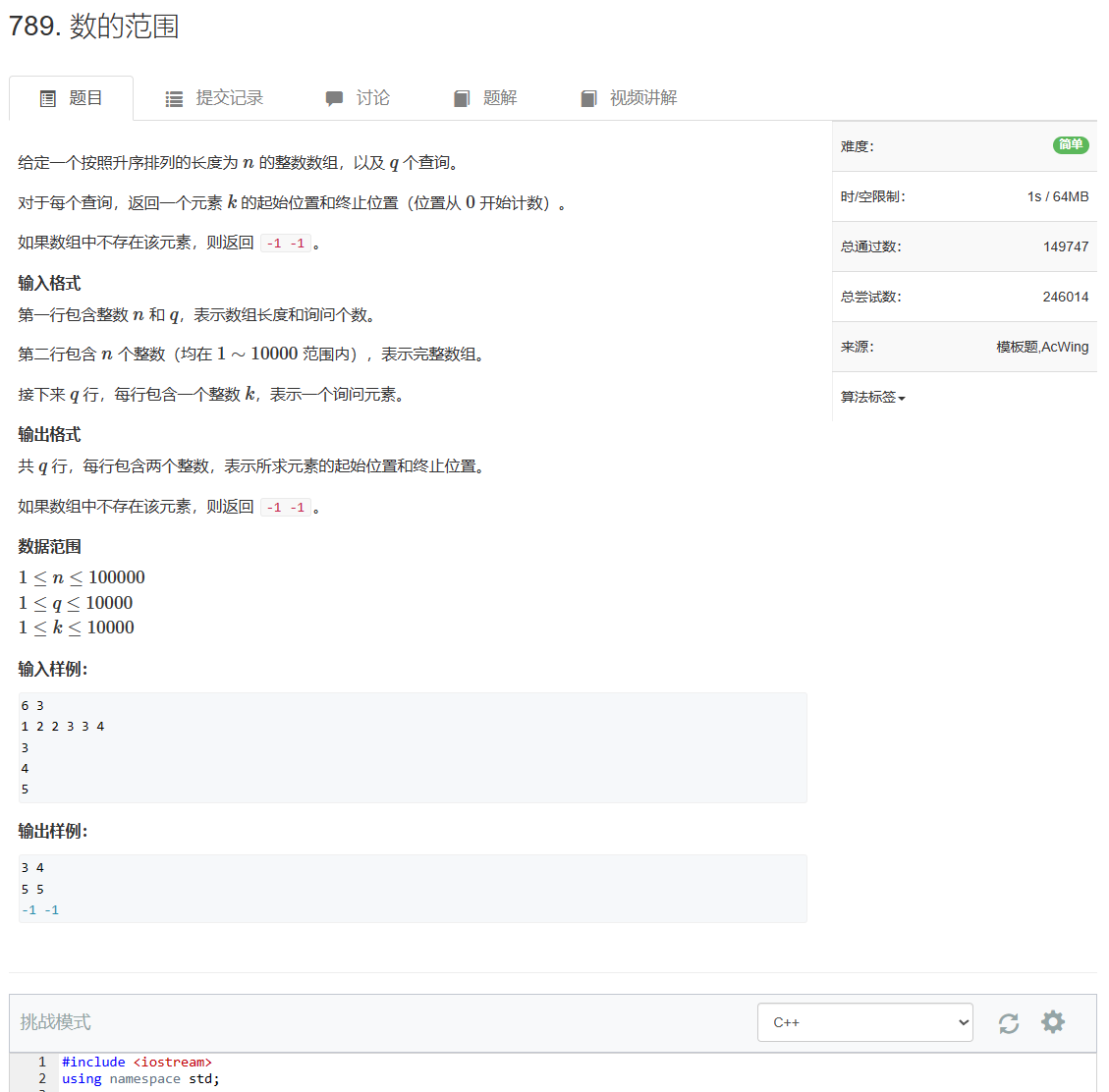
image.png

查询有序数组中，某个数所在的区间范围
首先确定check函数，整个数组可以划分成三个区间，>= x，<= x和== x
当然，这些区间之间有交集，先将check函数设置为>= x，找到第一个>= x的数.若该数不是x，则说明nums中没有x，题目无解，输出-1 -1
若找到了第一个>= x 的数，且该数为x，那么继续查找第一个<= x的数。此时将check设置为<= x

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int nums[N];
int n, x, count;

int main() 
{
    scanf("%d%d", &n, &count);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    while (count--)
    {
        scanf("%d", &x);
        int l = 0, r = n - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (nums[mid] >= x) r = mid;
            else l = mid + 1;    
        }
       
        if (nums[l] != x) printf("-1 -1\n");
        else
        {
            printf("%d ", l);
            int l = 0, r = n - 1;
            while (l < r)
            {
                int mid = l + r + 1 >> 1;
                if (nums[mid] <= x) l = mid;
                else r = mid - 1;
            }
            printf("%d\n", l);
        }
        
    }
    return 0;
}

790. 数的三次方根

790. 数的三次方根 - AcWing题库

#include <iostream>
using namespace std;

int main()
{
    double x;
    scanf("%lf", &x);
    double l = -10000.0, r = 10000.0;
    
    while (r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if (mid * mid * mid >= x) r = mid;
        else l = mid;
    }
    printf("%lf\n", l);
    return 0;
}

注意，r的值不能取x，若x为0.01时，正确答案为0.1。而二分的区间为[0, 0.01]此时取不到正确答案

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/667664.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Pandas-DataFrame常用基础知识点总结

Pandas-DataFrame常用基础知识点总结

注&#xff1a;以下知识点总结是将数据转为DataFrame格式数据的基础之上进行操作的 &#xff08;首先需要做的是将数据转为DataFrame格式&#xff09; DataFrame格式示例&#xff1a; import pandas as pd data {"code": [000008, 000009, 000021, 000027, 00003…
阅读更多...
代码随想录二刷 day28 | 回溯 之 93.复原IP地址 78.子集 90.子集II

代码随想录二刷 day28 | 回溯 之 93.复原IP地址 78.子集 90.子集II

day28 93.复原IP地址判断子串是否合法 78.子集回溯三部曲 90.子集II 93.复原IP地址 题目链接 解题思路&#xff1a; 切割问题就可以使用回溯搜索法把所有可能性搜出来 回溯三部曲 递归参数 startIndex一定是需要的&#xff0c;因为不能重复分割&#xff0c;记录下一层递归分…
阅读更多...
一种数据源切换的实践方案

一种数据源切换的实践方案

随着业务的不断深入&#xff0c;我们会碰见很多关于数据源切换的业务场景&#xff0c;数据源切换也是当前最常用的分库后的分流策略方式之一&#xff0c;对于读写职责分离的数据库集群而言&#xff0c;我们在服务层面制定相应的接口与数据库交互的定制化开发&#xff0c;也就是…
阅读更多...
云 cloud 高可用系统--在RDS上实现，从原理上不可能保证你100%不丢数据

云 cloud 高可用系统--在RDS上实现，从原理上不可能保证你100%不丢数据

我写这篇文字&#xff0c;实属无奈&#xff0c;在目前很多企业都依赖云的情况下&#xff0c;数据库的很多事情都是身不由己&#xff0c;发生问题&#xff0c;你查看日志&#xff0c;分析日志可能你连日志都不是全部的&#xff0c;并且想通过程序来过滤这个日志很多情况下都有限…
阅读更多...
数据库系统概述——第六章 关系数据理论（知识点复习+练习题）

数据库系统概述——第六章 关系数据理论（知识点复习+练习题）

&#x1f31f;博主&#xff1a;命运之光 &#x1f984;专栏&#xff1a;离散数学考前复习&#xff08;知识点题&#xff09; &#x1f353;专栏&#xff1a;概率论期末速成&#xff08;一套卷&#xff09; &#x1f433;专栏&#xff1a;数字电路考前复习 &#x1f99a;专栏&am…
阅读更多...
CMU 15-445 Project #2 - B+Tree（CHECKPOINT #1）

CMU 15-445 Project #2 - B+Tree（CHECKPOINT #1）

CHECKPOINT #1 一、题目链接二、准备工作三、部分实现1.查找操作2.插入操作3.删除操作 四、评测结果 一、题目链接 二、准备工作 见 CMU 15-445 Project #0 - C Primer 中的准备工作。 三、部分实现 对于B树的节点定义&#xff0c;通过节点类的命名 b_plus_tree_page 不难发现…
阅读更多...
linux-centos7操作系统查看系统未挂载的磁盘，挂载磁盘

linux-centos7操作系统查看系统未挂载的磁盘，挂载磁盘

linux-centos7操作系统查看系统未挂载的磁盘，挂载磁盘 查看当前磁盘空间 根目录 / 下也只有44G，其他目录只有10几G，正式环境肯定不够用 df -h查看硬盘数量和分区情况 fdisk -l查看到/dev/vdb 有500多G了 将/dev/vdb在分出一个区使用 第一步：编辑分区。执行命令fdisk …
阅读更多...
pr视频叠加，即原视频右上角添加另外一个视频方法，以及pr导出视频步骤

pr视频叠加，即原视频右上角添加另外一个视频方法，以及pr导出视频步骤

一、pr视频叠加&#xff0c;即原视频右上角添加另外一个视频方法 在使用pr制作视频时&#xff0c;我们希望在原视频的左上角或右上角同步播放另外一个视频&#xff0c;如下图所示&#xff1a; 具体方法为&#xff1a; 1、导入原视频&#xff0c;第一个放在v1位置&#xff0c;第…
阅读更多...
Selenium编写自动化用例的8种技巧

Selenium编写自动化用例的8种技巧

在开始自动化时&#xff0c;您可能会遇到各种可能包含在自动化代码中的方法&#xff0c;技术&#xff0c;框架和工具。有时&#xff0c;与提供更好的灵活性或解决问题的更好方法相比&#xff0c;这种多功能性导致代码更加复杂。在编写自动化代码时&#xff0c;重要的是我们能够…
阅读更多...
【序列dp】最长上升子序列（一）

【序列dp】最长上升子序列（一）

文章目录 最长上升子序列-序列dp概览895 最长上升子序列-O(n^2)1017 怪盗基德的滑翔翼1014 登山482 合唱队形1012 友好城市 最长上升子序列-序列dp 什么是序列相关的 DP &#xff1f;序列相关 DP&#xff0c;顾名思义&#xff0c;就是将动态规划算法用于数组或者字符串上&…
阅读更多...
textgen教程（持续更新ing...）

textgen教程（持续更新ing...）

诸神缄默不语-个人CSDN博文目录 官方GitHub项目&#xff1a;shibing624/textgen: TextGen: Implementation of Text Generation models, include LLaMA, BLOOM, GPT2, BART, T5, SongNet and so on. 文本生成模型&#xff0c;实现了包括LLaMA&#xff0c;ChatGLM&#xff0c;B…
阅读更多...
C++课程学习记录

C++课程学习记录

目录 1. 前置说明2. 二叉树的模拟2.1 参考资料2.2 二叉树的构建2.2.1 递归构建2.2.2 迭代构建 2.3 二叉树的遍历2.4 二叉树的应用 3. 继承与派生3.1 最简单的生死3.2 动态申请空间的生死3.3 继承中的protectd权限3.4 三种继承方式3.5 修改某些继承成员的继承类型3.6 多级派生3.…
阅读更多...
C++57个入门知识点_番外1_C++指针偏移在类中的应用及指针偏移原理

C++57个入门知识点_番外1_C++指针偏移在类中的应用及指针偏移原理

这是对C指针偏移介绍比较好的博文&#xff0c;但是比较分散&#xff0c;我把其进行了整理&#xff0c;原博文地址请见最后&#xff0c;讲的很详细。 C57个入门知识点_番外1_C指针偏移在类中的应用及指针偏移原理 1. C指针偏移原理2. C显示十进制内存地址&#xff08;不用理解&…
阅读更多...
AQS原理

AQS原理

目录 一、原理概述二、AQS 对资源的共享方式三、AQS底层使用了模板方法模式四、使用demo&#xff0c;使用AQS实现不可重入锁五、AQS使用到的几个框架 一、原理概述 AQS全称是 AbstractQueuedSynchronizer&#xff0c;是阻塞式锁和相关的同步器工具的框架 AQS核心思想是&#…
阅读更多...
Appian低代码平台

Appian低代码平台

国外老牌低代码开发平台Appian Appian在国内用的比较少&#xff0c;资料也很匮乏。需要自己主动去官网寻找。 Appian 学习平台 进入Appian Community可以选择学习路径&#xff0c;可以选择适合自己的学习路径&#xff1b;我选择的是Builder路径&#xff0c; 看了足足80个小…
阅读更多...
opencv检测二维码和条形码

opencv检测二维码和条形码

文章目录 1 excel制作简单二维码2 识别二维码和条形码2.1 相关库2.2 decode解码2.3 圈出二维码的位置2.4 判断二维码是否授权 3 完整代码3.1 使用图片进行识别3.2 使用摄像头实时识别 4 总结 1 excel制作简单二维码 使用excel可以实现制作二维码&#xff0c;但只能实现做英文和…
阅读更多...
基于51单片机的简易电子琴设计

基于51单片机的简易电子琴设计

目录 摘 要 基于51单片机的简易电子琴设计 一、系统设计 1、项目概要 2.设计任务和基本要求 二、硬件设计 1、硬件设计概要 2、时钟振荡电路模块 3.复位电路模块 5.数码管电路模块 6.蜂鸣器模块 7、乐曲切换电路模块 三、软件原理 四、软件流程图 五、代码实现 …
阅读更多...
解析Transformer基本结构与实现

解析Transformer基本结构与实现

1.基本结构 ​ Transformer总体架构可分为4个部分&#xff1a; 输入部分-输出部分-编码器部分-解码器部分 输入部分包含&#xff1a; 原文本嵌入层&#xff08;Input embedding&#xff09;及其位置编码(position encoding)目标文本嵌入层及其位置编码器 文本嵌入层的作…
阅读更多...
TCP/UDP协议重温三次握手四次挥手 简单笔记

TCP/UDP协议重温三次握手四次挥手 简单笔记

术语储备&#xff1a; SYN&#xff1a;同步位 &#xff1b;SYN1,表示进行一个连接请求 ACK&#xff1a;确认位 &#xff1b;ACK1,确认有效 ACK0&#xff0c;确认无效 ack : 确认号 &#xff1b;对方发送序号1 seq &#xff1a; 序号 ; 标识从TCP发端向TCP收端发送的数据字节流 …
阅读更多...
基于JPA的Repository使用详解

基于JPA的Repository使用详解

Spring Data JPA Spring Data是Spring提供的操作数据的框架&#xff0c;Spring Data JPA是Spring Data的一个模块&#xff0c;通过Spring data 基于jpa标准操作数据的模块。 Spring Data的核心能力&#xff0c;就是基于JPA操作数据&#xff0c;并且可以简化操作持久层的代码。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023