二叉搜索树，也叫二叉查找树、二叉排序树，是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

注意：二叉搜索树中序遍历的结果是有序的
本系列博文将通过一些力扣算法题目学习TypeScirpt，这篇将以二叉搜索树为主题边学习TypeScipt边实战算法。（部分算法思想参考于程序员Carl:代码随想录）

一、判断二叉搜索树

1.1、题目描述

力扣链接：https://leetcode.cn/problems/validate-binary-search-tree/
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

1.2、题解

本题有一个极容易掉进的陷阱：不能单纯的比较左节点小于中间节点，右节点大于中间节点。

因为，可能存在一种情况就是，虽然对每个节点来说左子节点都小于右子节点，但左子树不一定都小于右子树,如：

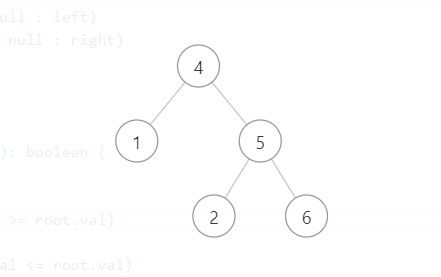
因为二叉搜索树要判断的是左子树的点一定都小于右子树的点。
这一题最直观的方法就是中根遍历，只要遍历出的数组是递增的，则满足二叉搜索树：

function isValidBST(root: TreeNode | null): boolean {
    const traveseArr: number[] = [];
    if(root === null)
        return true;
    else traverse(root);
    function traverse(root: TreeNode | null){
        if(root === null)
            return;
        traverse(root.left);
        traveseArr.push(root.val);
        traverse(root.right);
    }
    for (let i = 0, length = traveseArr.length; i < length - 1; i++) {
        if (traveseArr[i] >= traveseArr[i + 1]) return false;
    }
    return true;
}

二、二叉搜索树中的众数

2.1、题目描述

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

力扣链接：https://leetcode.cn/problems/find-mode-in-binary-search-tree

2.2、题解

首先使用任意遍历方法将树遍历（前、中、后或者层序），然后将遍历出的数字都存入数组当中。

问题就变成了求一个数组当中的众数，要注意的是这个数组里可能有多个众数，即出现同样次数的数字不止一个，比如1,2,2,2,3,3,3或者1,2,2,3,3,4。

要求众数，我们可以用到哈希Map，算出数组内所有数出现的次数，我们设计一个存储出现次数的哈希Map，遍历一遍：

   for(let i = 0; i < traveseArr.length; i++){
        countMap.set(traveseArr[i], (countMap.get(traveseArr[i]) || 0) + 1);
  }

key表示出现的数字，value表示对应出现的次数，然后找到出现次数最多的key输出就好了。题解：

function findMode(root: TreeNode | null): number[] {
    if (root === null) return [];
    const countMap: Map<number, number> = new Map();
    const traveseArr: number[] = [];
    traverse(root);

    function traverse(root: TreeNode | null){
        if(root === null)
            return;
        traverse(root.left);
        traveseArr.push(root.val);
        traverse(root.right);
    }
    
    for(let i = 0; i < traveseArr.length; i++){
        countMap.set(traveseArr[i], (countMap.get(traveseArr[i]) || 0) + 1);
    }
    const countArr: number[][] = Array.from(countMap);
    countArr.sort((a, b) => {
        return b[1] - a[1];
    })
    const resArr: number[] = [];
    const maxCount: number = countArr[0][1];
    for (let i of countArr) {
        if (i[1] === maxCount) resArr.push(i[0]);
    }
    return resArr;
};

在代码中使用到了， const countArr: number[][] = Array.from(countMap);，可以将countMap（类型为哈希Map）转换成二维数组，数组为一个n行2列数组，第一列为出现的数字，第二列为对应数字出现的次数，这样就可以很好进行操作并得到众数了。

三、求二叉搜索树的最近公共祖先

3.1、题目描述

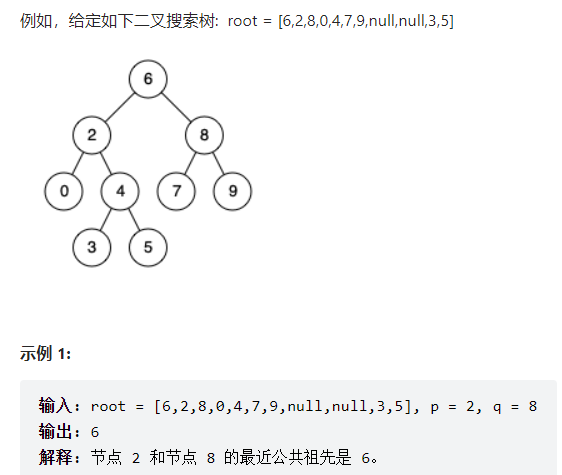
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

力扣链接：https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/

3.2、题解

首先我们做一题普通二叉树的最近公共祖先，可以用递归来做，最近公共祖先有一个特点就是：p和q来自于（1）左子树，（2）右子树，（3）根节点的三者其中之二。

function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
	if(root == null)
        return root;
    if(root == p || root == q)
        return root;
    const left = lowestCommonAncestor(root.left, p, q);
    const right = lowestCommonAncestor(root.right, p, q);
    // 即第一次在该节点的左子树和右子树上分别找到了p 和 q
    if(left !== null && right !== null) return root;
    // 暂时只找到一个
    if(left != null) return left;
    if(right != null) return right;
    // 一个都没找到
    return null;
};

而 求二叉搜索树的最近公共祖先 需要在上一题的基础上，利用一下“二叉搜索树是有序的”这个特点，即从根开始找，如果根节点大于p也大于q，则往左子树找，如果根节点小于q也小于p，则往右子树找，如果不满足同时小于或者大于，那么他就是我们要的最近公共祖先。

function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
	if(root.val > p.val && root.val > q.val){
        return lowestCommonAncestor(root.left, p , q);
    }
    if(root.val < p.val && root.val <q.val){
        return lowestCommonAncestor(root.right, p, q);
    }
    return root;
};

四、二叉搜索树中的插入操作

4.1、题目描述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果
力扣链接：https://leetcode.cn/problems/insert-into-a-binary-search-tree

4.2、题解

我们选择不改变树的结构，而是往空结点里面插值，这样做就简单很多，首先判断当前根节点为不为空，若为空则新建一个值为val的结点，返回，若不为空则判断其根节点的值是大于val还是小于val，使用递归的思想，根值大于val就去改左子树，根值小于val就去改右子树。

function insertIntoBST(root: TreeNode | null, val: number): TreeNode | null {
    if(root == null){
        let res: TreeNode =  new TreeNode(val)
        return res;
    }

    if(root.val > val)
        root.left = insertIntoBST(root.left, val);
    else if(root.val < val)
        root.right =insertIntoBST(root.right, val);
    return root;
};

五、删除二叉搜索树中的节点

5.1、题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

力扣链接：https://leetcode.cn/problems/delete-node-in-a-bst

5.2、题解

一般来说，删除节点可分为两个步骤：首先找到需要删除的节点；如果找到了，删除它。我们主要把算法分成三大块：删除节点的部分、寻找待删除节点的部分，递归返回的部分。

可以利用到二叉搜索树的特性寻找到待删除节点，然后删除节点的方法是把右子树的根节点提上来带他当前节点，然后右子树的最左子节点的左节点接当前左子树。

function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
    if (root === null) return null;
    //删除节点
    if(root.val === key){
        if (root.left === null && root.right === null) return null;
        else if (root.left === null) return root.right;
        else if (root.right === null) return root.left;
        // 把右子树的最左子节点续上
        let curNode: TreeNode = root.right;
        while (curNode.left !== null) {
            curNode = curNode.left;
        }
        curNode.left = root.left;
        return root.right;
    }
    //寻找节点
    else if(root.val < key){
        root.right = deleteNode(root.right, key);
    }
    else if(root.val > key){
        root.left = deleteNode(root.left, key);
    }
    //返回
    return root;
};

六、修剪二叉搜索树

6.1、题目描述

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。
题目链接：https://leetcode.cn/problems/trim-a-binary-search-tree/

6.2、题解

如果当前节点值小于low，则切除左子树以及根节点，如果当前节点值大于high，则切除右子树以及根节点，如果当前节点值在low和high的其中，那么就递归到左子树和右子树进行后续操作。

function trimBST(root: TreeNode | null, low: number, high: number): TreeNode | null {
    if (root === null) return null;
    if (root.val < low) {
        return trimBST(root.right, low, high);
    }
    if (root.val > high) {
        return trimBST(root.left, low, high);
    }
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
};

七、将有序数组转换为二叉搜索树

7.1、题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

力扣链接：https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree

7.2、题解

使用二分法加递归的思想，首先要保证高度平衡，且在满足二叉搜索树的前提下，根节点需要选择为该有序数组的中间值，然后左子树即是该值左边的部分，右子树则是其右边的部分，递归继续即可：

function sortedArrayToBST(nums: number[]): TreeNode | null {
    if(nums == null)
        return null;
    else 
        return recur(nums, 0, nums.length - 1);
    function recur(nums:number[], left:number, right:number):TreeNode{
        if(left === right){
            let res:TreeNode = new TreeNode(nums[left]);
            return res;
        }
        if(left > right)
            return null;
        let mid = Math.floor((right + left + 1) / 2);
        let res:TreeNode = new TreeNode(nums[mid]);
        res.left = recur(nums, left, mid - 1);
        res.right = recur(nums, mid + 1 , right);
        return res;
    }
};

八、把二叉搜索树转换为累加树

8.1、题目描述

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

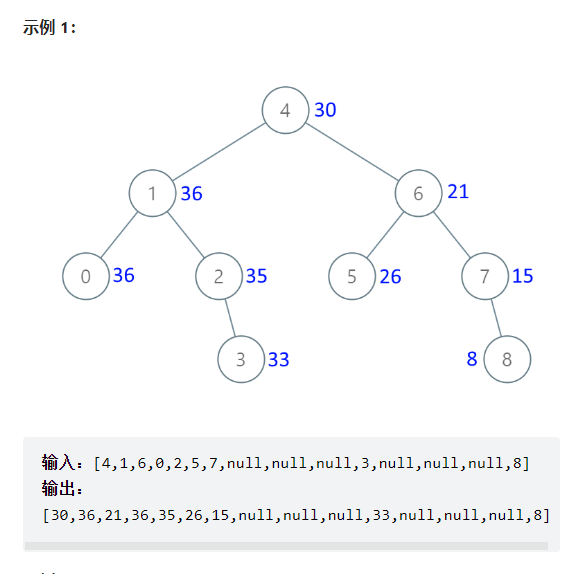
力扣链接：https://leetcode.cn/problems/convert-bst-to-greater-tree

8.2、题解

从累加的顺序来看，很简单能看出，累加树的累加顺序是：右=>中=>左，然后设计一个值，在遍历的时候进行累加就好了:

function convertBST(root: TreeNode | null): TreeNode | null {
    let preNum:number = 0;
    recur(root);
    function recur(root: TreeNode | null){
        if (root === null) return;
        recur(root.right);
        root.val += preNum;
        preNum = root.val;
        recur(root.left);
    }
    return root;
};

最后

💖 个人简介：人工智能领域研究生，目前主攻文本生成图像（text to image）方向

📝 关注我：中杯可乐多加冰

🔥 限时免费订阅：TypeScript实战

📝 加入社群 抱团学习：中杯可乐的答疑交流群

🎉 支持我：点赞👍+收藏⭐️+留言📝