Perspective Projection(透视投影)

延续上节课的内容：
通常使用aspect ratin(长宽比) 和 **field-of-view(垂直可视角度)**来描述透视投影的视锥。

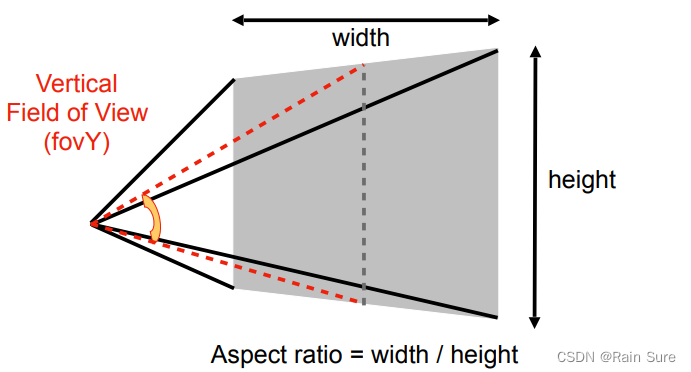
可以通过fovY来转化到$l,r,b,t$：

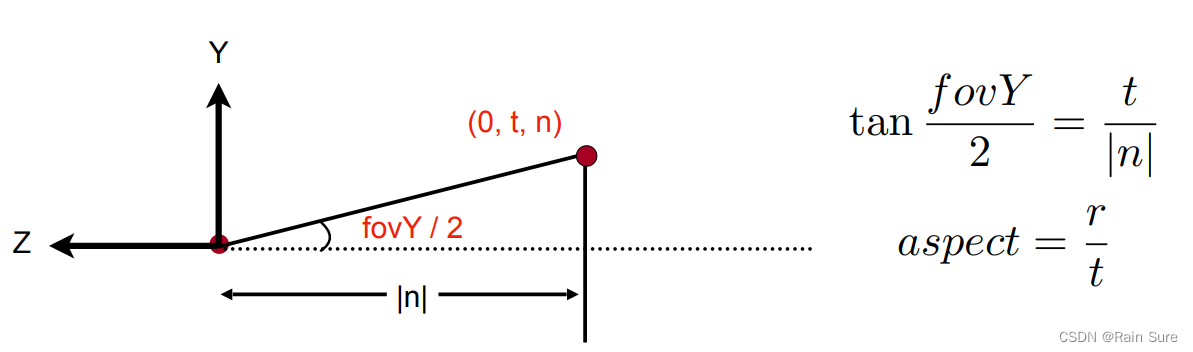
Canonical Cube to Screen(从标准立方体到屏幕)

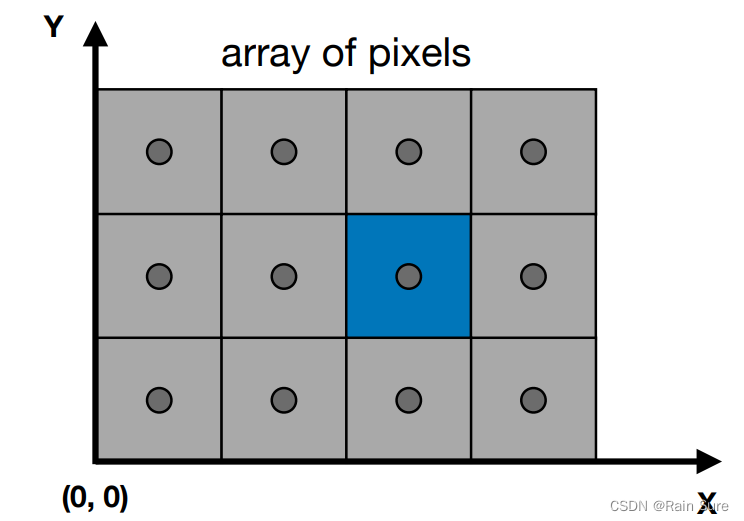
What is a screen(什么是屏幕)?

• 一个二维数组，数组中的每个元素都是一个像素
• 数组的大小就是分辨率
• 一个典型的光栅成像设备

把东西画在屏幕上的过程就是光栅化。

Pixel(像素)：
一个个小方块有着完全相同的颜色，一个像素内的颜色可以用$(R,G,B)$来表示。

屏幕空间：
屏幕左下角是原点，右边是$x$轴正方向，上边是$y$轴正方向，与《虎书》定义略有区别。
像素$(x,y)$的中心是$(x+0.5,y+0.5)$。

将立方体画到屏幕上的过程：

• 忽略$z$方向的坐标。
• 在$xy$平面进行转化：$[-1,1{]}^2$ 变为$[0,width]\times [0,height]$
• 变换矩阵如下：
  $M_{\text{viewport }}=\left(\begin{array}{cccc}\frac{\text{ width }}{2}& 0& 0& \frac{\text{ width }}{2}\\ 0& \frac{\text{ height }}{2}& 0& \frac{\text{ height }}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$

Rasterization: Drawing to Raster Displays(如何在光栅设备上画东西)

Triangles - Fundamental Shape Primitives(三角形-基本形状的基元)

Why triangles?（为什么是三角形？）

• 三角形是最基本的多边形
• 可以将其它多边形拆成三角形
• 具有一些独特的性质：
  • 三角形内部一定是平面的
  • 三角形的内外的定义是非常清晰的
  • 可以通过三个顶点进行插值，得到三角形内部各个点的属性(重心坐标插值)

将三角形变为像素

一种简单的方法：采样(Sampling)

将一个函数离散化的过程：

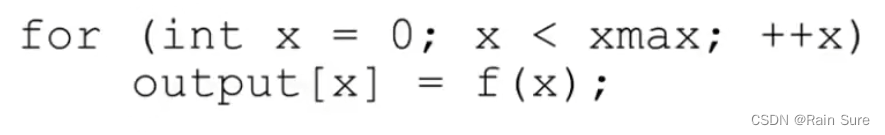
我们可以定义一个函数$inside(t,x,y)$，来判断一个指定的像素是否在三角形内部：


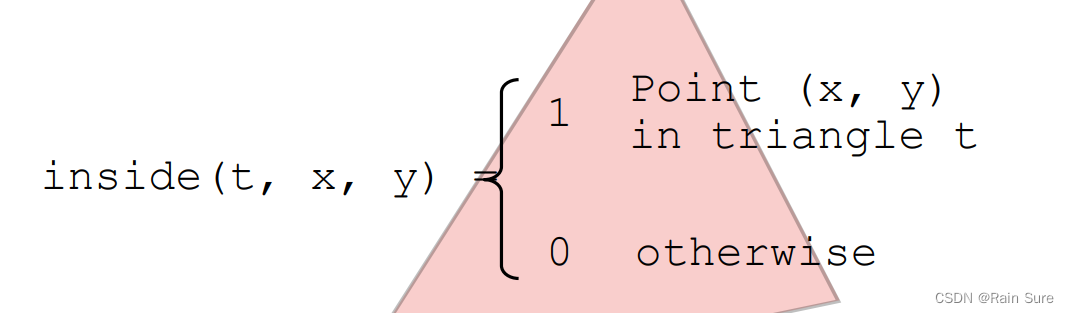
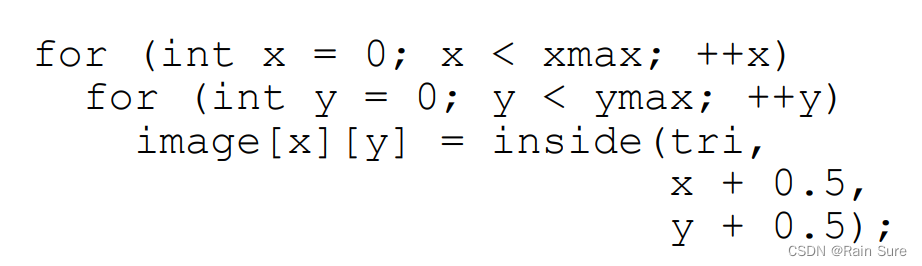
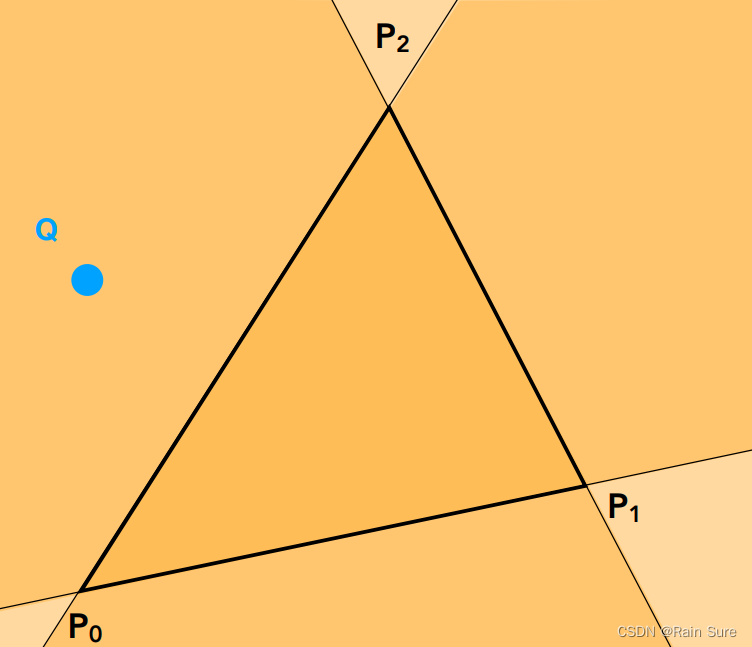
如何判定一个点是否在三角形内部呢？
通过叉积
叉积可以判定两个向量的左右关系，如果一个点全部在三条边的同一侧，那么该点就在三角形内部。

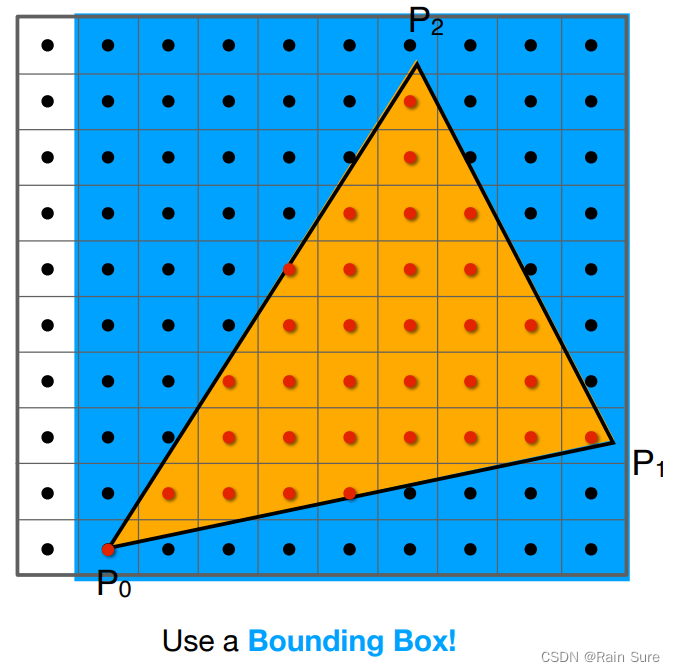
通常不需要检查屏幕上的全部像素，我们只需要判断包围盒内部的像素：

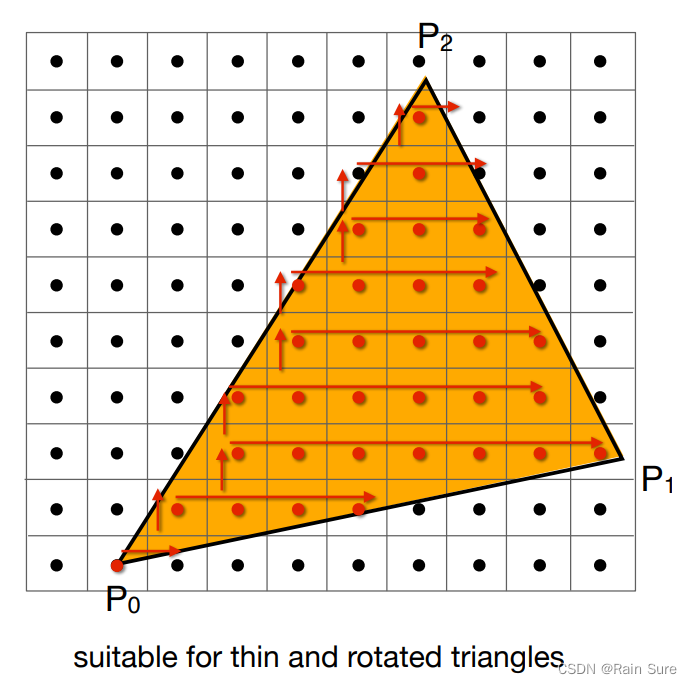
加速方法：
每一行只找到最左和最右，开始扫描：

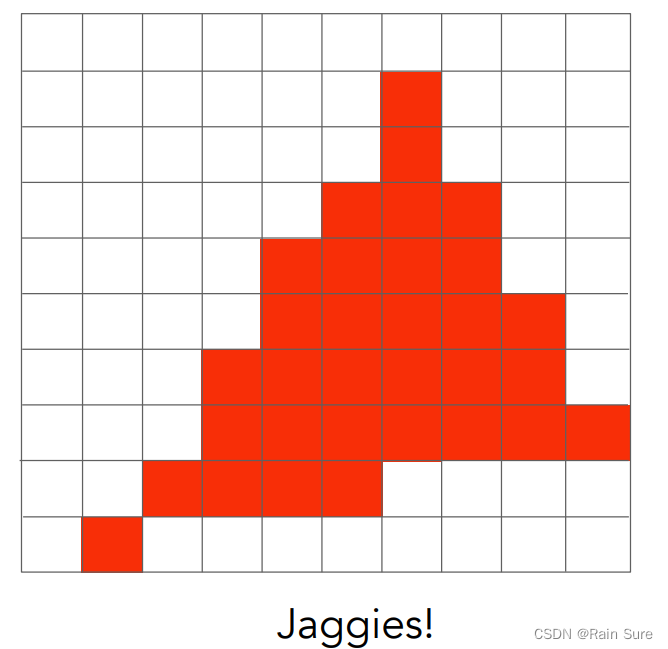
因为像素本身有一定的大小，和采样率不够高导致图像出现了锯齿：

参考资源

GAMES101 Lecture05