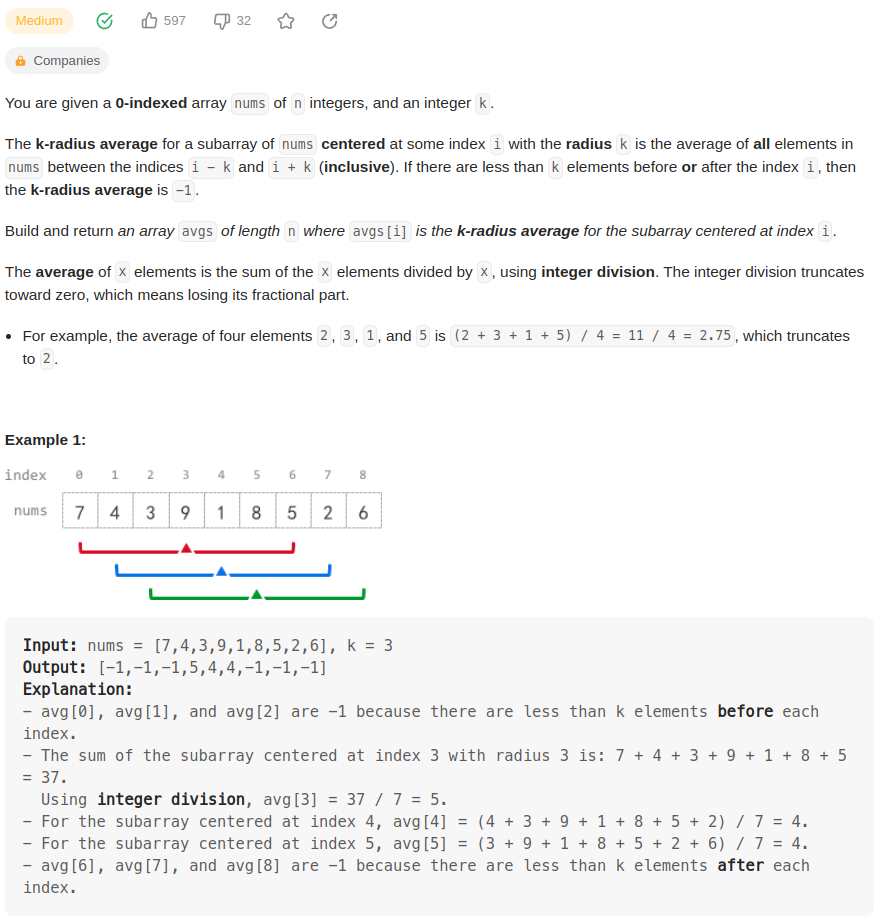
k半径长度的子数组表示以数组下标 i 为中心，[i-k, i+k]范围内的子数组。
返回和数组nums一样长度的数组res，res[i] = [i-k, i+k]范围内的元素和 / 元素个数2k+1
如果 i-k 或者 i+k 超出了数组范围，res[i] = -1.

思路：

如果[i - k, i+k] 超出了数组范围， i处值为-1，
那么如果数组的长度 < 2k+1, 无论取哪个 i , [i-k, i+k]都会超出数组范围，这时返回全是-1的数组。

如果k = 0, 那么[i-k, i+k]就是i 本身，直接返回原数组nums.

如果i-k超出数组范围，也就是i-k < 0, 所以 i < k处全部填上-1.
同理 i + k > n-1时超出数组右边范围，所以 i > n-k-1处全部填上-1.
现在只需要看 i = k ~ n-k 范围内的。

涉及到一个范围内的数组求和，用到积分数组.
那么res[i] = (acc[i+k] - acc[i-k-1]) / (2k+1)

注意nums[i]最大到10⁵, 数组长度最大达到10⁵, 所以积分数组acc用long型防止溢出。

public int[] getAverages(int[] nums, int k) {
    int n = nums.length;
    if(k == 0) return nums;
    int[] res = new int[n];
    if(n < (2*k + 1)) {
        Arrays.fill(res, -1);
        return res;
    }

    long[] acc = new long[n+1];
    for(int i = 0; i < n; i++) {
        acc[i+1] = acc[i] + nums[i];
    }

    Arrays.fill(res, 0, k, -1);
    Arrays.fill(res, n-k, n, -1);
    int divide = 2*k+1;

    for(int i = k; i < n-k; i++) {
         res[i] = (int)((acc[i+k+1]-acc[i-k])/divide);
    }
    return res;
}