索引
1.什么是索引
- 数据库概论老师说:索引就是教科书的目录页,你要查哪个内容你就去目录页查询内容在哪。
- Mysql官网:索引是帮助Mysql高效获取数据的排好序的数据结构。
2.索引的数据结构
- 二叉树
- 红黑树
- Hash表
- B-Tree
2.1 二叉树
我们先看如下这组数据:
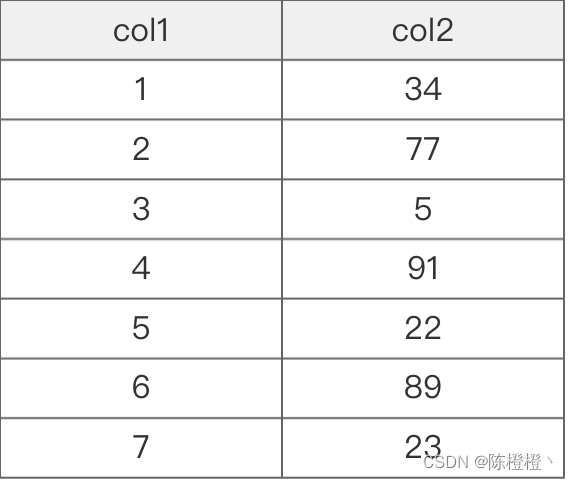
假设上述为Mysql中的一张表,存在两列col1、col2且数据如上,现在需要执行一条sql
select * from table where table.col2 = 89;
正常情况下,假设这张表中不存在任何索引,它可能需要一行行的进行匹配,这里有人会问,这些数据不都是挨着一块的吗查询起来应该也很快,这里解释一下:
大伙都知道,Mysql中的数据都是存在我们磁盘上的,磁盘写入数据是一个磁道一个磁道的进行写入,可能我们在今天向Mysql中插入一条col1为1的这一条数据,数据分布在磁盘上的某个位置A,过了好几天在插入col1为2的这条数据,数据分布在磁盘上的某个位置B,这时间间隔内,我们计算机的任何程序都可能往磁盘上进行写入数据,所以,Mysql的数据是在磁盘上随机分布,不一定是紧挨着的,之所以能通过select直观的看到,是mysql将这些数据汇集起来了。
因此我们执行上述Sql的时候需要和磁盘进行IO交互,然后这些IO交互的效率是不高的,所以我们需要一个办法减少这个IO交互次数或者将这个次数控制在一定范围内,因此索引就出现了。
我们将上述col2的数据使用二叉树进行排列
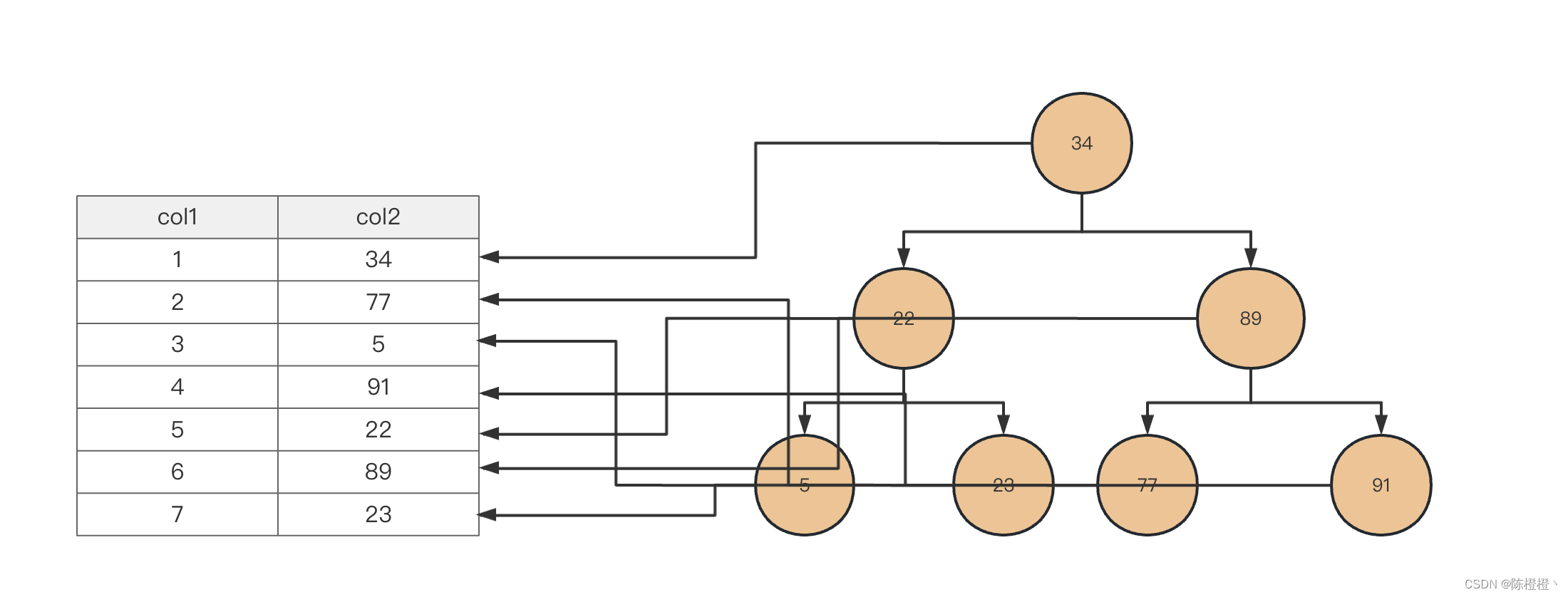
这里的二叉树的结构每个节点都有个key:value,这里的key存在的数据的值(索引),然后value是存储的是索引所在行数据在文件磁盘的地址(例如:0x07),一般来说树结构的数据查询都是从根节点开始查找,二叉树的特点是树的右边的元素大于父元素,左边的元素小于父元素的,根据这个特性我们来在来分析上述sql。
select * from table where table.col2 = 89;
需要查询的索引值为89,从根节点开始34小于索引值,去右边查找发现第一个元素就是我们需要的,这样只需要经过2次查找就能找出我们的需要的数据,上第一次分析中不存在索引的情况下,我们至少需要6次扫描才能找到,这样索引的效果显而易见。
然后Mysql底层并不是使用二叉树,为什么呢?我们看如下Sql
select * from table where table.col1 = 6;
我们分析col1有存在什么特点,类似于自增ID,数据值依次递增,一般来说索引会是提前维护好,那么我们将col1进行构建索引,那么二叉树维护的索引数据结构是什么样子呢,根据二叉树右边大于左边的特性,如下:
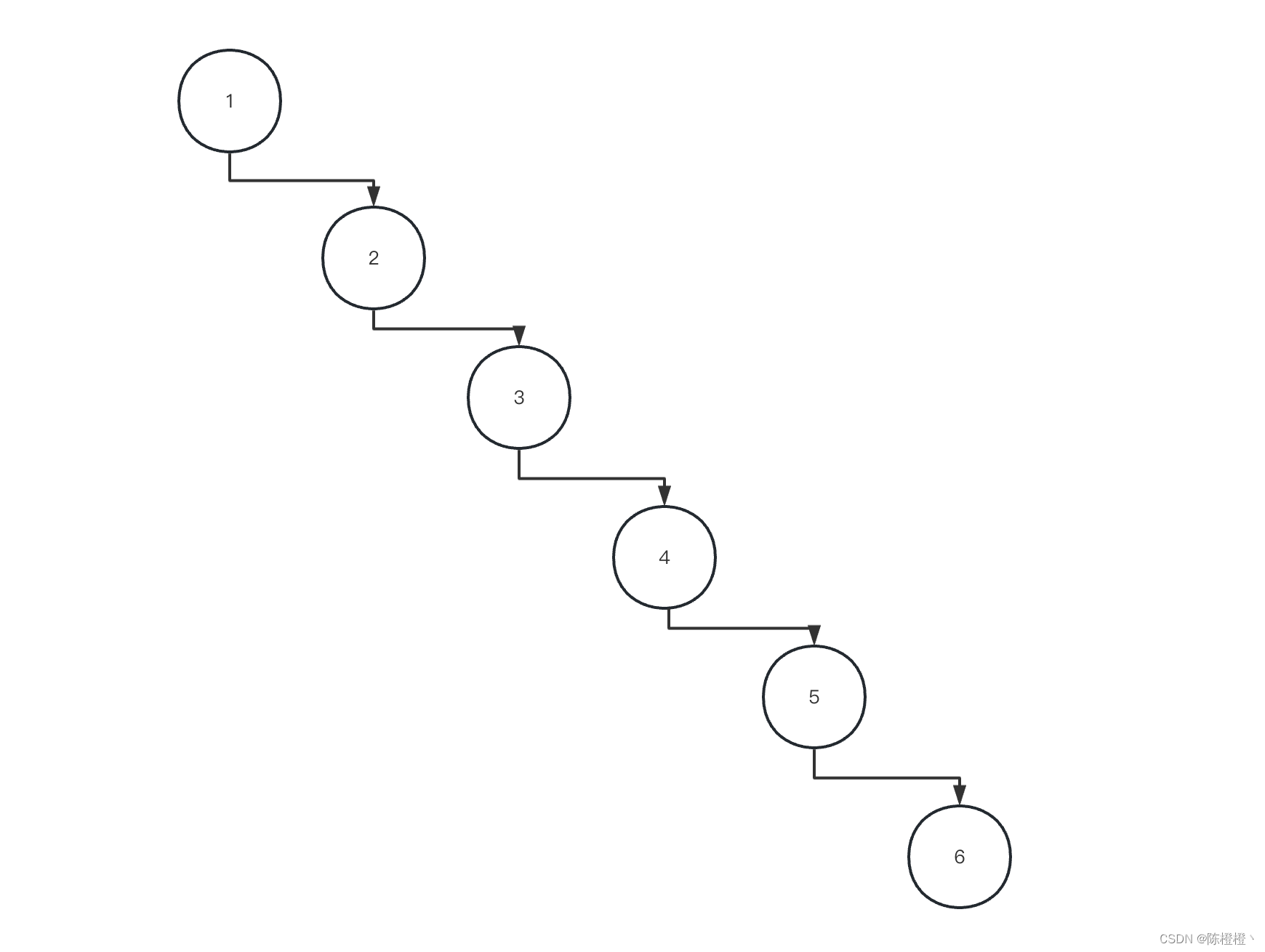
你会发现这个实际上是一个链表,索引也是存储在磁盘上,我们查询col1=6的数据使用索引和不使用索引进行全表扫描没有任何的性能的提升,因此二叉树对这种单表增长的列数据用二叉树建立索引没有任何效果的提升。
那么有没有好的解决方案呢?如下
2.2 红黑树
红黑树(平衡二叉树)我们来看一下上述数据使用红黑树是如何去维护的如下:
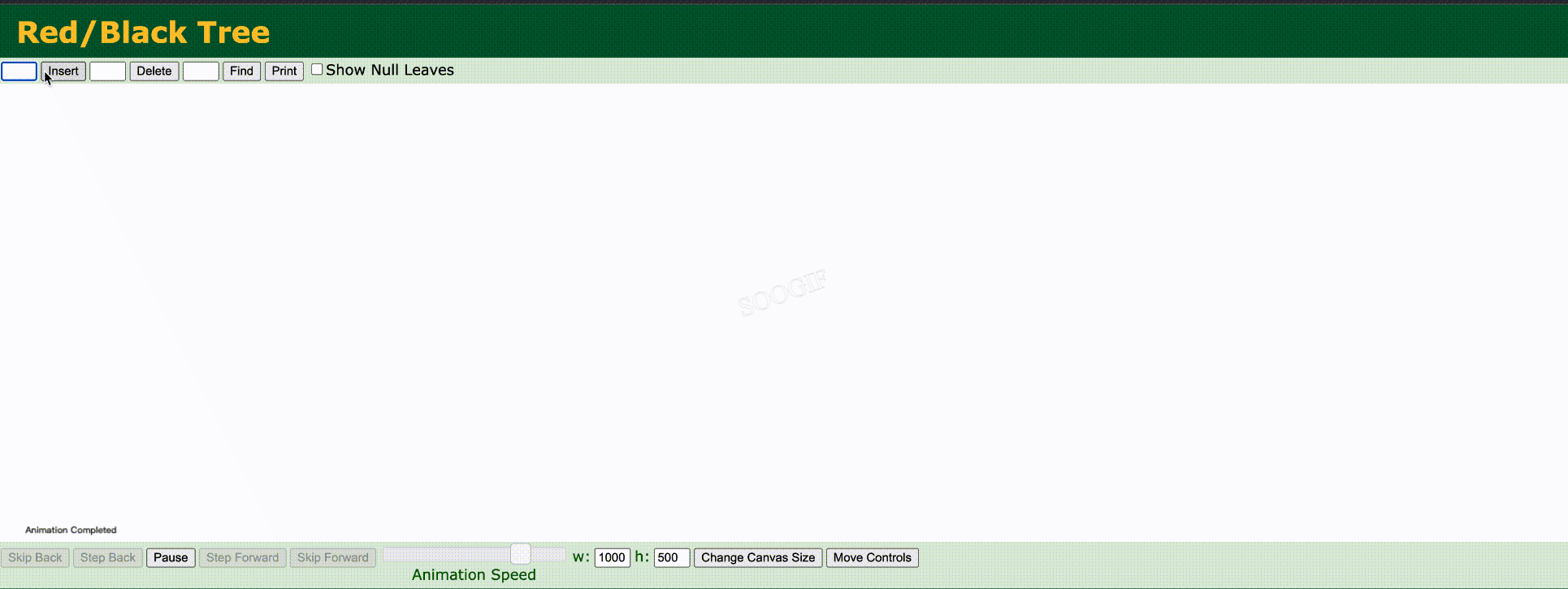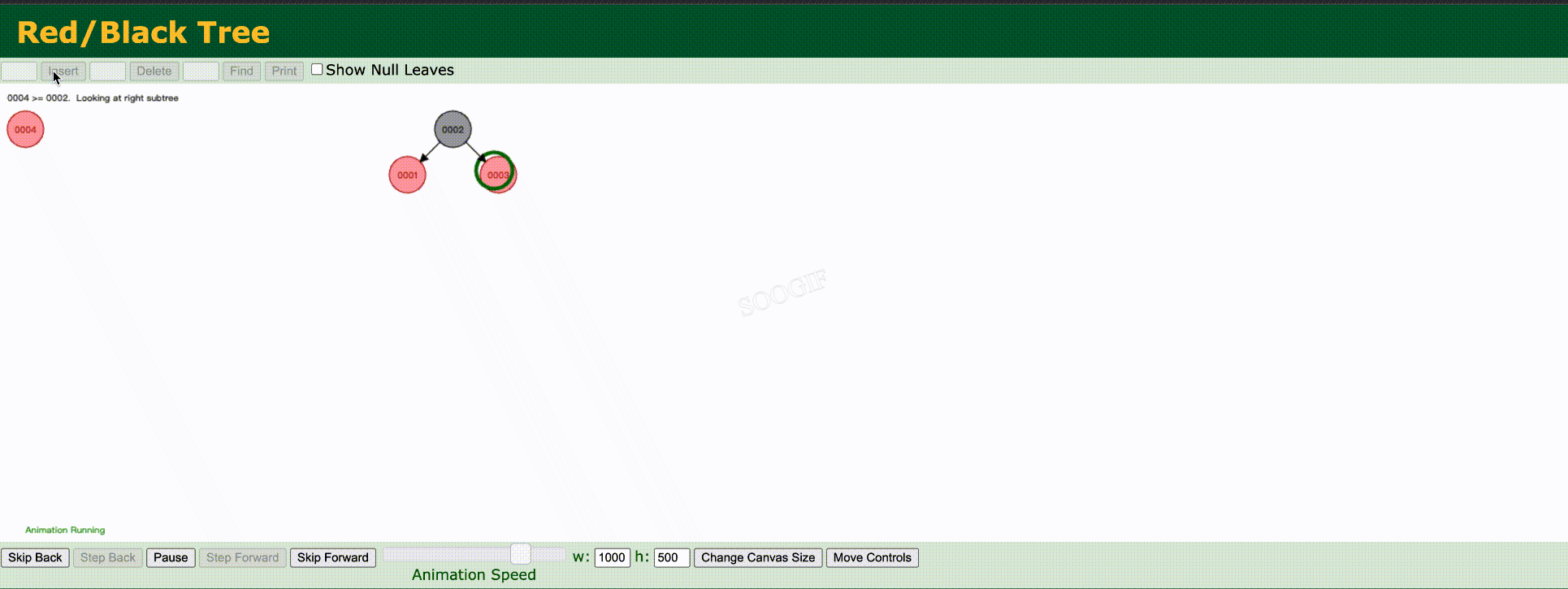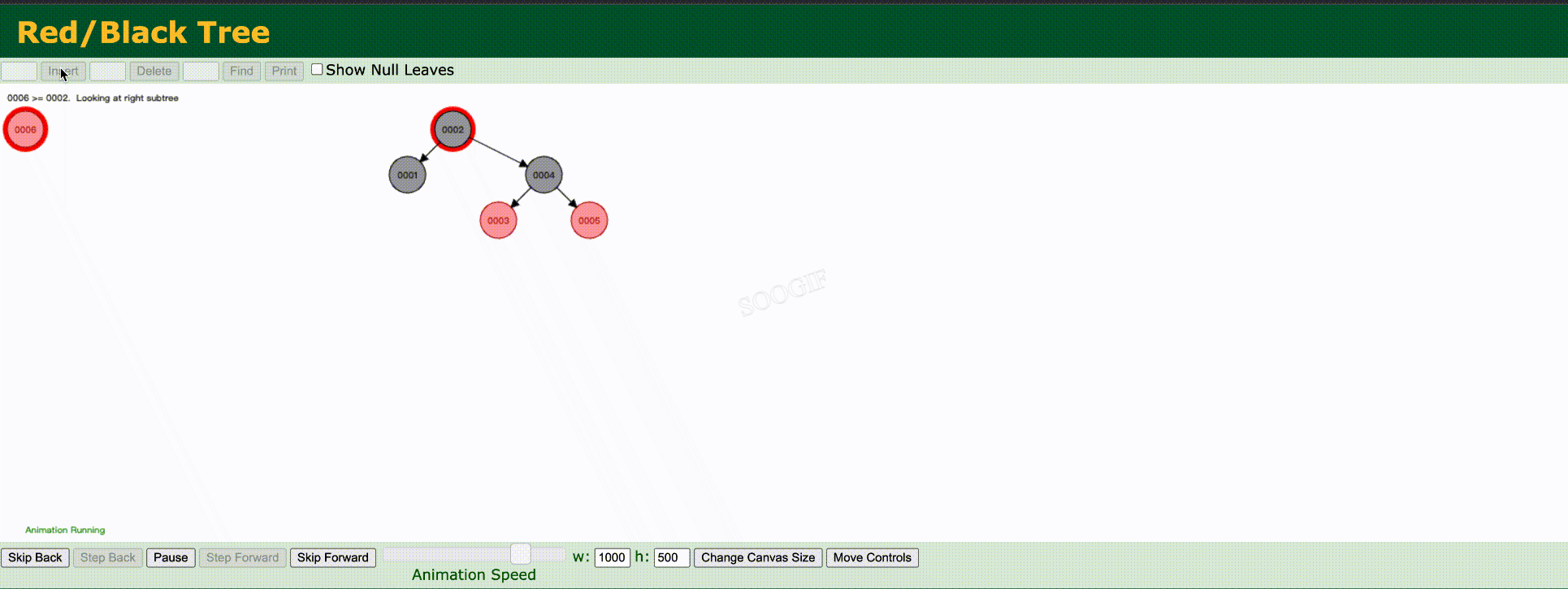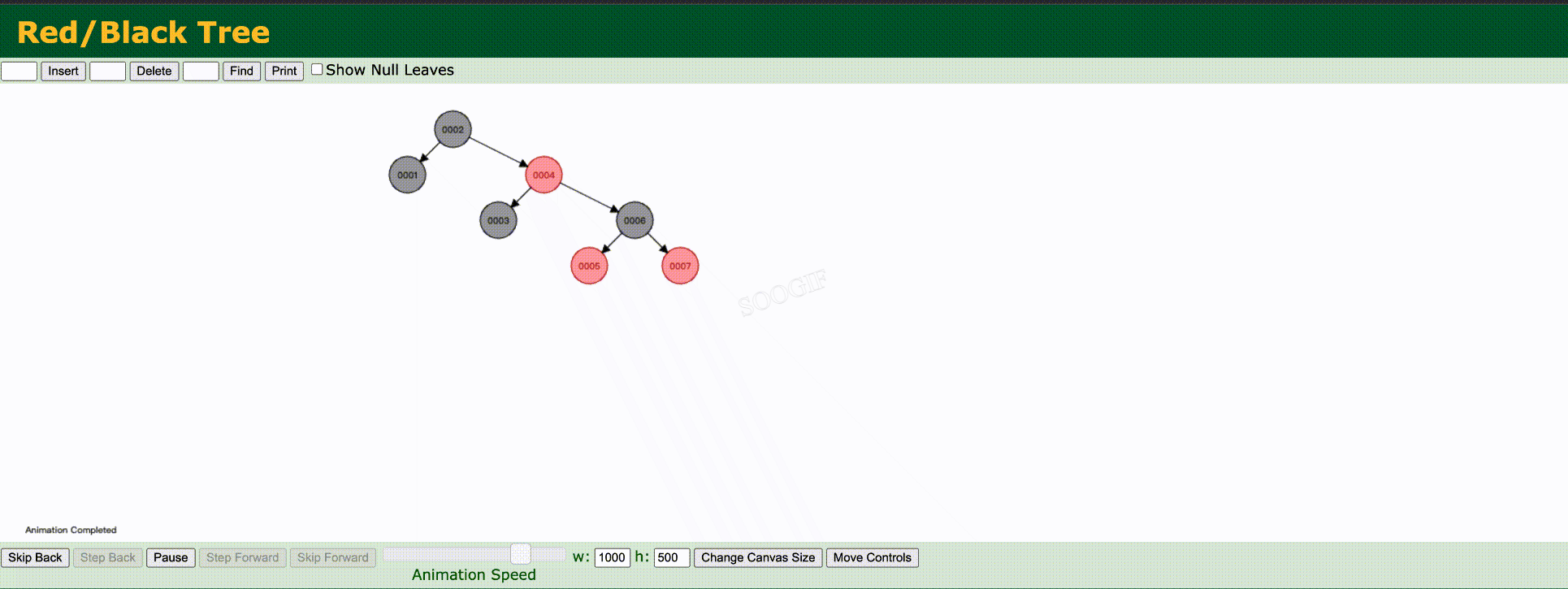
最终数据结构:
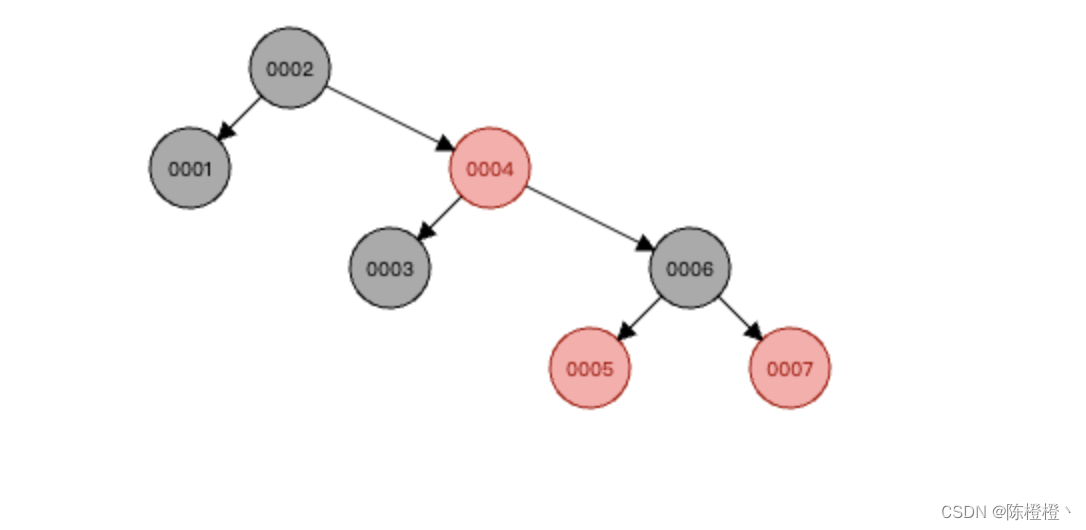
从上述图中我们可以看到,红黑树其实解决了二叉树单边增长的数据链式的问题,当一边的节点比另一边的节点数量多2节点的时候,它会自己做一次平衡。那么为什么Mysql的底层不使用红黑树作为索引的数据结构呢?其实原因之一就是红黑树的高度是不可控制的,这里我们只有7条数据,假设我们有500万条数据,那么树的高度最大接近于2log(n+1),n就是节点数量500W。这样看来其实如果用红黑树作为Mysql的索引数据结构,其实带来的效率提升也不是特别的明显。
那么红黑树解决了二叉树单边增长的问题,那么有没有一种数据来解决红黑树高度的问题呢?如下:
2.3 B-Tree
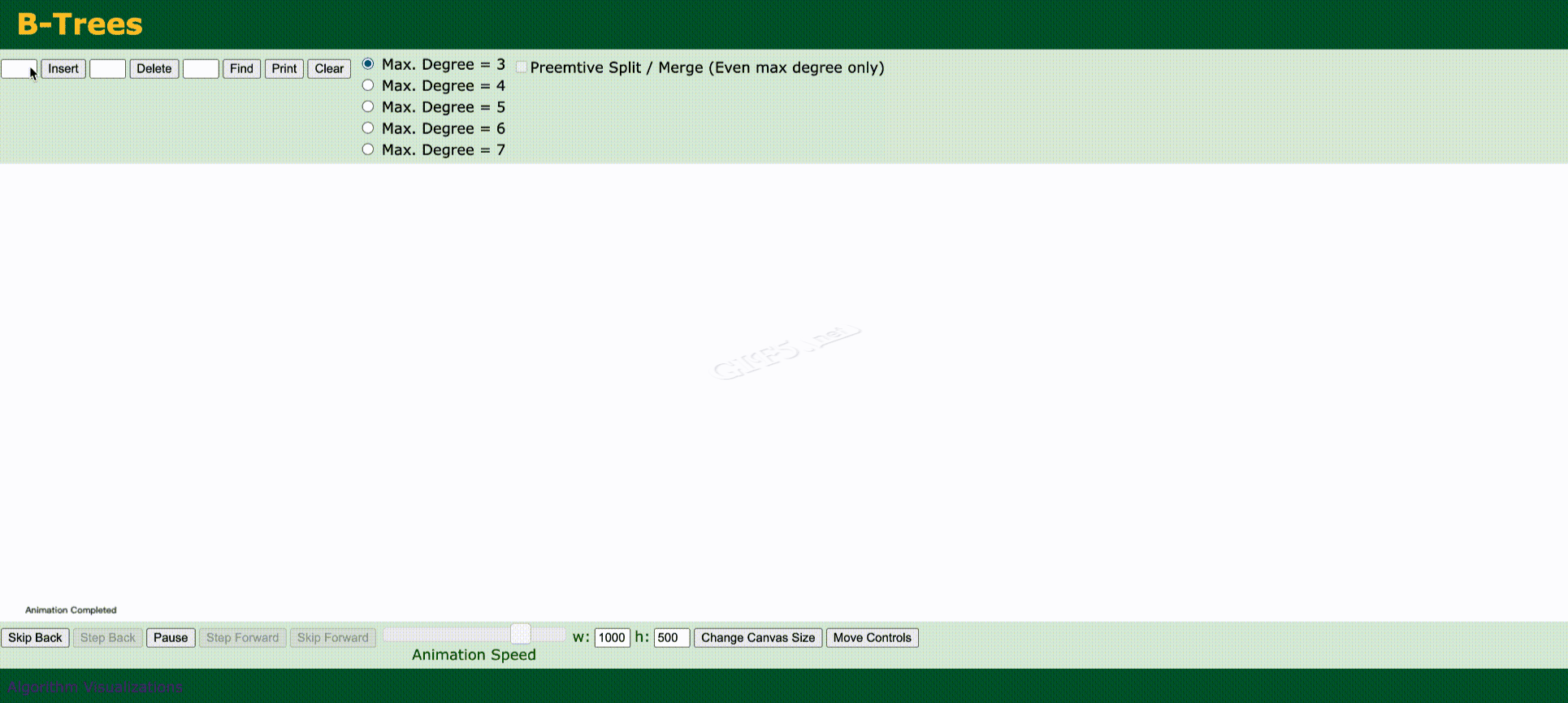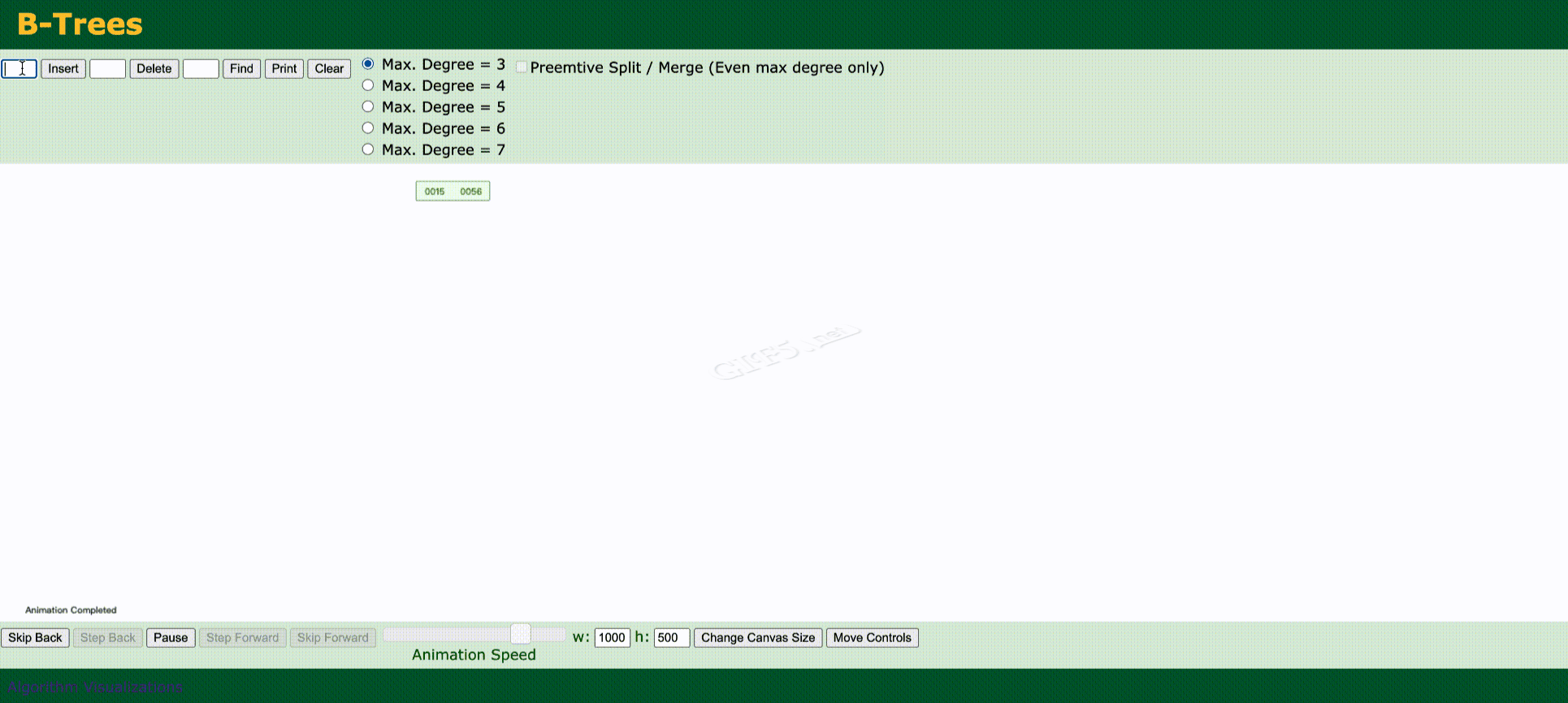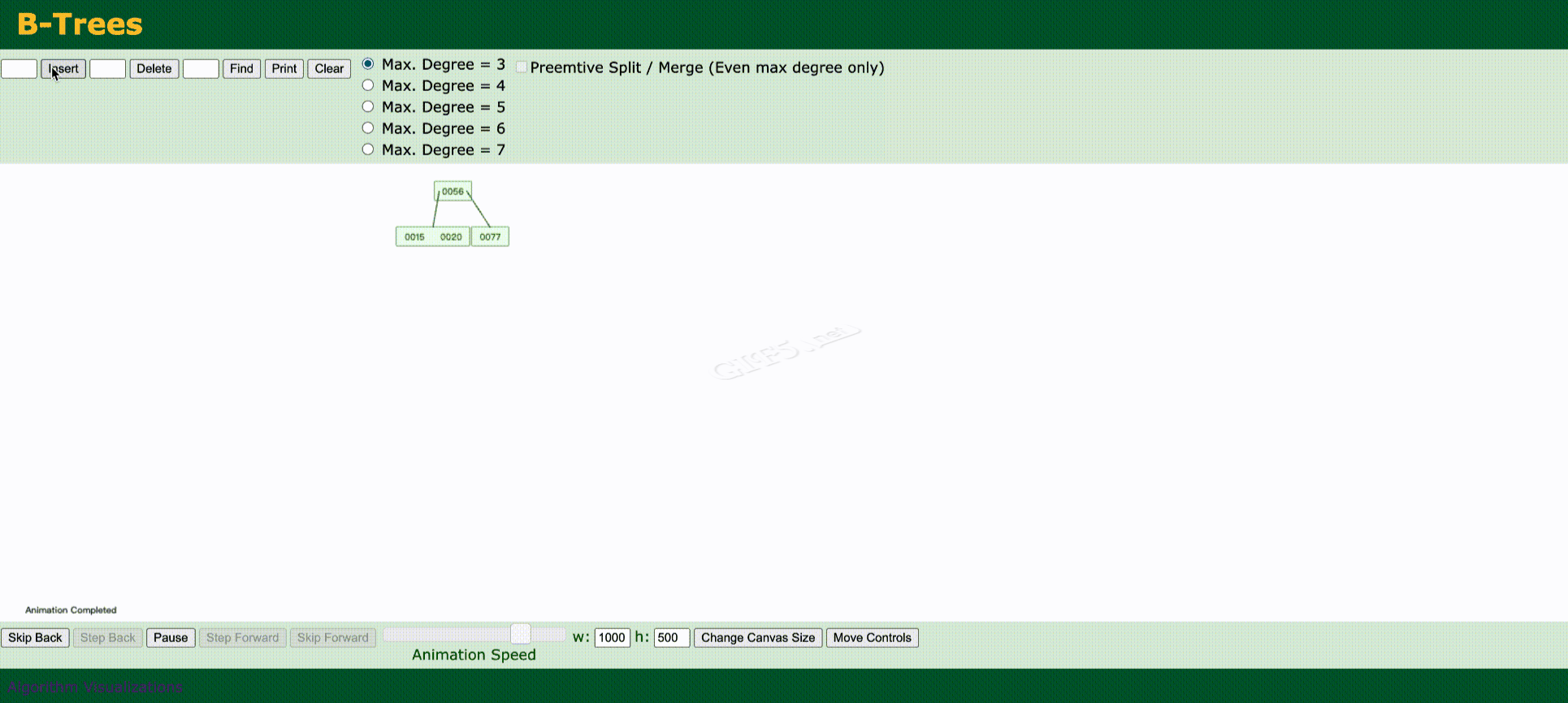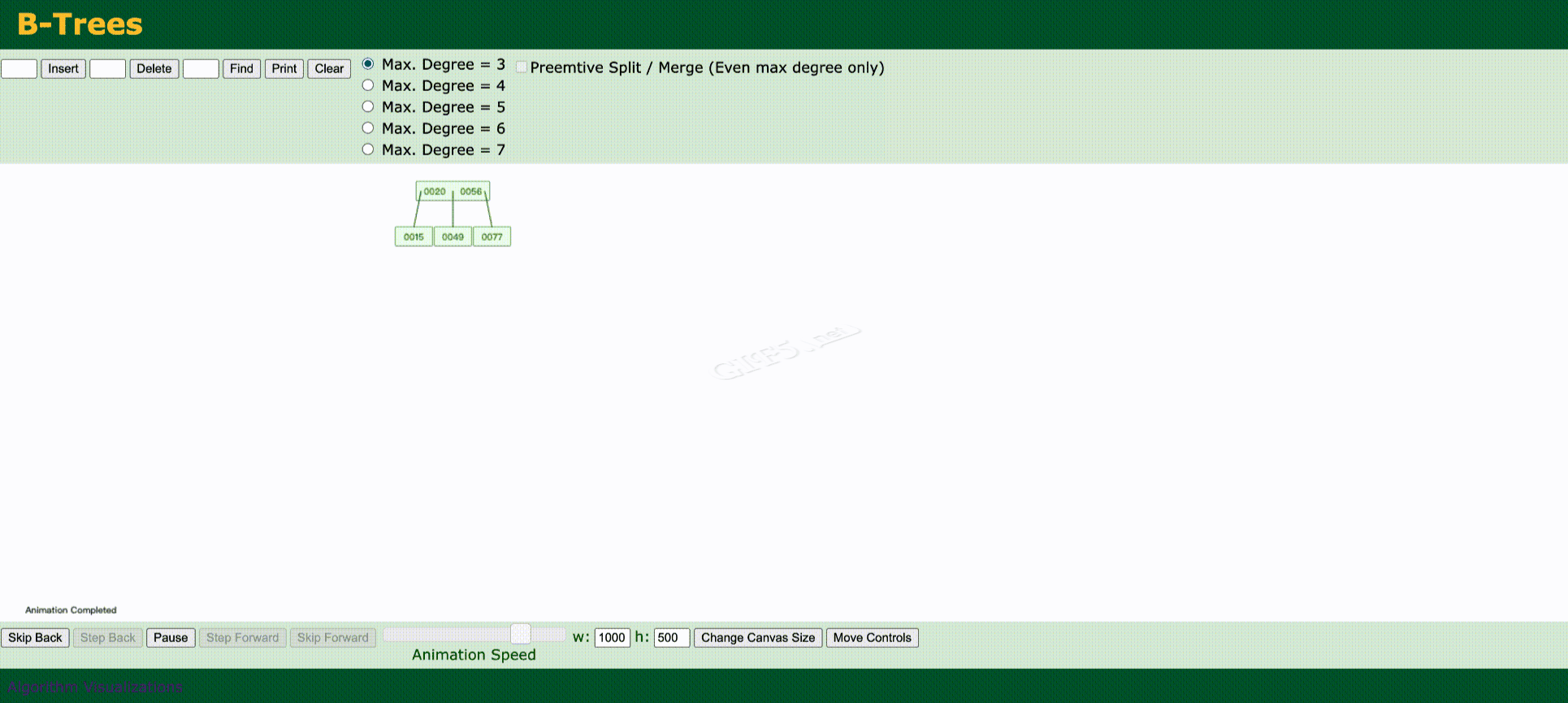
B-Tree
- 叶节点具有相同的深度,叶节点的指针为空
- 所有索引元素不重复
- 节点中的数据索引从左到右递增排列
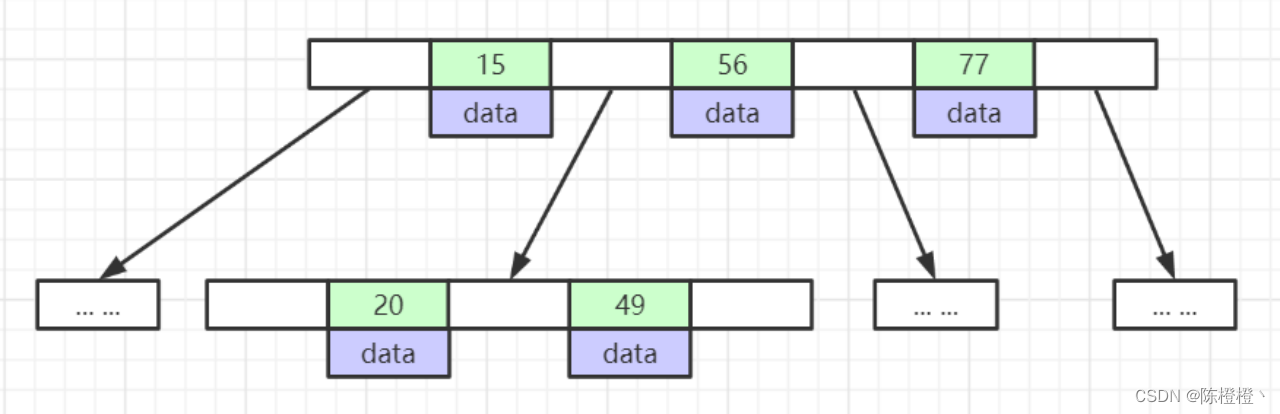
我们来看一下上述的数据,B-Tree是如何去维护的。
实际上Mysql最终仍然不是使用B-Tree来作为索引,而是B+Tree,我们先来看一下B+Tree
2.4 B+Tree
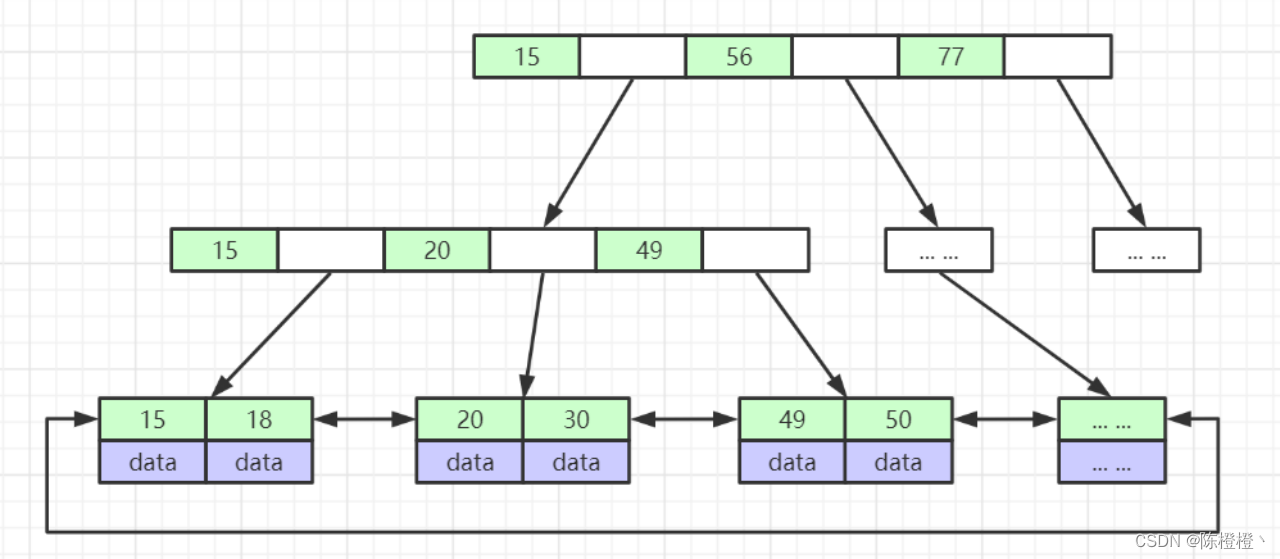
我们再来看下B+Tree最终是如何维护这些数据的,如下图;
B-Tree和B+Tree都是常用的一种数据结构,他们主要的区别如下:
结构不同:B-Tree是一种平衡树,每个节点包含键值和指向子节点的指针;而B+Tree是一种多路平衡树,每个节点只包含键值,而子节点的指针都存储在叶子节点中。
叶子节点不同:B-Tree的叶子节点既包含键值也包含数据,而B+Tree的叶子节点只包含键值和指向数据的指针。
遍历方式不同:B-Tree的遍历方式是深度优先遍历,而B+Tree的遍历方式是广度优先遍历。
应用场景不同:B-Tree适用于需要随机访问的场景,如文件系统和数据库索引;而B+Tree适用于需要顺序访问的场景,如范围查询和排序。
总的来说,B+Tree相对于B-Tree具有更高的磁盘利用率和更快的范围查询速度,因此在关系型数据库中被广泛使用。
2.4.B+Tree是如何解决树高度问题
对比上面的红黑树和B+Tree来看,我们知道了红黑树弊端是因为他的高度无法进行控制,那么BTree是如何解决这个问题的呢?
首先我们来看下,B+Tree是如何去查找数据的,如上图,假设我们查找25。(这里我们规定树的高度为3)
1.第一次磁盘IO,加载出第一行索引(页)到内存,在二分法进行数据定位,发现数据在20-49这个区间。
2.第二次磁盘IO,加载出20-49索引区间数据,在二分法进行查找,确认叶子节点数据。
3.第三次磁盘IO,加载叶子节点数据,进行查找数据,叶子节点可能会存储整行数据也有可能是索引所在磁盘空间地址(和数据库引擎有关,后面文章会提到)。
这里我们模拟了整个搜索过程,需要注意的是使用二分法在内存中进行数据比对的开销要远远小于一次磁盘IO的时间,这里会有疑问既然这样,那么为什么不把所有数据存放到一行呢,这里存放到一行的话,如果存在几千万条数据,可能内存吃不消。那么Mysql为什么这样设计呢?
2.4.1索引页
在上面我们提到了一个索引页,索引页是可以横向扩充数据的并且数据是排好序的,那么索引页能存放多少索引数据呢。
SHOW GLOBAL STATUS LIKE 'Innodb_page_size'

查询出来的结果大约是16KB的数据,那么16KB能够存放多少数据呢,我们来算下假设数据类型为bigint,一个bigint为8b,然后会有一块空间存放下一个索引页的内存地址(图中箭头指的空白处)在C语言中,这里分配的空间大约为6b,也就是一个索引大约占用14b,16380b/(8b+6b)=1170,大约能存储1170个数据,第一行、第二行类似,我们假设高度为三,那么第三行存储的就是叶子节点了,叶子节点上是有data具体的数据,这个上面也提到了和数据库引擎有关系,但是一般来说1KB的数据足以存储mysql中的一行数据了,也就是说他能存储16条数据。
那么一个高度为3的B+Tree总共能存储的数据量为1170117016=21902400,两千多万条数据。