子集

力扣链接

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。
解集不能包含重复的子集。你可以按任意顺序返回解集。

示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：
输入：nums = [0]
输出：[[],[0]]

提示：
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素互不相同

题目理解

一看就是 回溯组合 , 那么跟回溯组合有什么不同呢?

回溯组合中的, 接收结果是在叶子节点, 而这个子集是收集各个节点上的数据

步骤

树形结构

递归函数

首先, 还是两个全局变量, 一个记录单层结果, 一个记录全部结果

vector<int> path; // 记录单层结果
vector<vector<int>> result; // 记录全部结果

函数返回的类型是 void, 组合 — — startindex

void backtracking(vector<int>& nums, int startindex)

递归结束的条件

由于是要收集每个节点上的数据, 所以我们就可以不用写条件, 直接收录

result.push_back(path);

单层逻辑

单层逻辑和回溯组合中的单层逻辑是一样的

for(int i = startindex; i < nums.size(); i++)
{
	path.push_back(nums[i]);
	backtracking(nums, i + 1);
	path.pop_back();
}

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
 
    void backtracking(vector<int>& nums, int startindex)
    {
        result.push_back(path);
        
        for(int i = startindex; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
    
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        backtracking(nums, 0);
        return result;
        
    }
};

子集II

力扣链接

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。

示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2：
输入：nums = [0]
输出：[[],[0]]

提示：
1 <= nums.length <= 10
-10 <= nums[i] <= 10

题目理解

哈哈, 跟上面的子集大体上是一样的, 唯一不同的是 有重复的元素 && 解集不能包含重复的子集
那么下一步的操作肯定就是 去重

步骤

树形结构

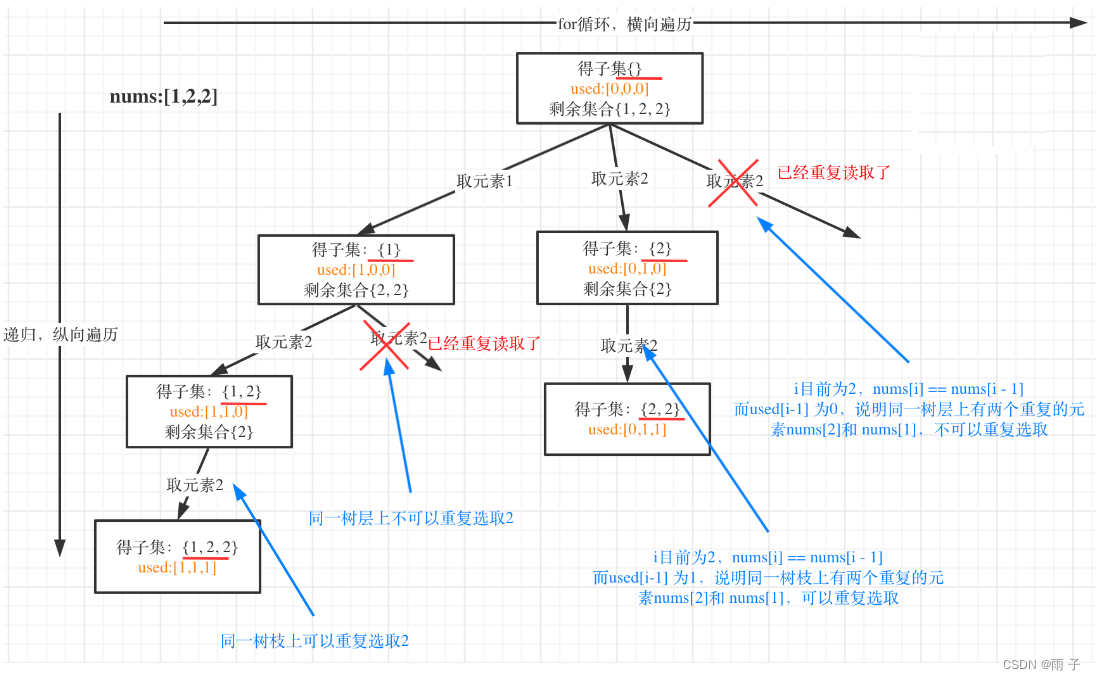
从上面的树形图可以看出:

同一树层上的 2 要去重 — — 树层去重
同一树枝上的 2 不能去重 — — 树枝不去重

树层去重, 树枝不去重的原因:
树层去重 — — 因为已经排序, 那么第一个 2 具有的组合包含了后面的 2 具有的组合
树枝不去重 — — 因为 [1, 2 ] 和 [1, 2, 2] 是两个不同的结果, 一个是第一个 2, 一个是第二个 2

递归函数

首先, 还是两个全局变量, 一个记录单层结果, 一个记录全部结果

vector<int> path; // 记录单层结果
vector<vector<int>> result; // 记录全部结果

函数返回的类型是 void
组合 — — startindex
去重 — — used数组

void backtracking(vector<int>& nums, vector<bool>& used, int startindex)

递归结束的条件

由于是要收集每个节点上的数据, 所以我们就可以不用写条件, 直接收录

result.push_back(path);

单层逻辑

子集 + 去重

  for(int i = startindex; i < nums.size(); i++)
  {
      // 树层去重, 树枝不去重的关键
      if(i > 0 && ( nums[i] == nums[i - 1] ) && (used[i - 1] == false))
      {
          continue;
      }
      
      path.push_back(nums[i]);
      used[i] = true;
      backtracking(nums, used, i + 1);
      path.pop_back();
      used[i] = false;
  }

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    
    void backtracking(vector<int>& nums, vector<bool>& used, int startindex)
    {
        // 子集是搜集每一个节点, 不需要结束条件
        result.push_back(path);
        
        for(int i = startindex; i < nums.size(); i++)
        {
            // 树层去重, 树枝不去重的关键
            if(i > 0 && ( nums[i] == nums[i - 1] ) && (used[i - 1] == false))
            {
                continue;
            }
            
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, used, i + 1);
            path.pop_back();
            used[i] = false;
        }
    }
    
    vector<vector<int>> subsetsWithDup(vector<int>& nums) 
    {
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end());  // 排序很重要
        backtracking(nums, used, 0);
        
        return result;
        
    }
};