注1:本文系“简要介绍”系列之一,仅从概念上对快速傅里叶变换进行非常简要的介绍,不适合用于深入和详细的了解。
快速傅里叶变换:从原理到应用
Denoising Data with Fast Fourier Transform
1. 背景介绍
傅里叶变换(Fourier Transform, FT)在信号处理、图像处理、通信、计算机科学等领域有着广泛的应用。然而,传统的傅里叶变换计算过程复杂度较高,难以满足实际应用需求。为解决这一问题,**快速傅里叶变换(Fast Fourier Transform, FFT)**应运而生。本文将对快速傅里叶变换的原理、研究现状、挑战和未来展望进行简要介绍。
2. 原理介绍和推导
2.1 傅里叶变换
傅里叶变换的基本思想是将一个信号从时域表示转换为频域表示。具体来说,傅里叶变换将连续时间信号转换为其频谱表示,而傅里叶逆变换则将频谱表示转换回时域信号。傅里叶变换的数学表达式如下:
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-j\omega t} dt F(ω)=∫−∞∞f(t)e−jωtdt
2.2 离散傅里叶变换
实际应用中,信号通常是离散的,因此我们需要使用 离散傅里叶变换(Discrete Fourier Transform, DFT)。DFT将离散时间信号转换为离散频谱表示,其数学表达式如下:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π N n k X[k] = \sum_{n=0}^{N-1} x[n] e^{-j\frac{2\pi}{N} nk} X[k]=n=0∑N−1x[n]e−jN2πnk
然而,DFT的计算复杂度为 O ( N 2 ) O(N^2) O(N2),这在处理大规模数据时计算效率较低。
2.3 快速傅里叶变换
快速傅里叶变换 是一种优化算法,通过分治策略降低DFT的计算复杂度。FFT将信号分为奇数和偶数部分,递归地计算这两部分的DFT,然后合并结果得到最终的DFT。FFT的计算复杂度为 O ( N log N ) O(N\log{N}) O(NlogN)。
假设 x [ n ] x[n] x[n]是一个长度为 N N N的离散信号,我们可以将其分为偶数部分 x e [ n ] x_e[n] xe[n]和奇数部分 x o [ n ] x_o[n] xo[n]:
x e [ n ] = x [ 2 n ] , x o [ n ] = x [ 2 n + 1 ] x_e[n] = x[2n], \quad x_o[n] = x[2n+1] xe[n]=x[2n],xo[n]=x[2n+1]
递归地计算 x e [ n ] x_e[n] xe[n]和 x o [ n ] x_o[n] xo[n]的DFT,记为 X e [ k ] X_e[k] Xe[k]和 X o [ k ] X_o[k] Xo[k],我们可以得到:
X [ k ] = X e [ k ] + e − j 2 π N k X o [ k ] , k = 0 , 1 , … , N − 1 X[k] = X_e[k] + e^{-j\frac{2\pi}{N} k}X_o[k], \quad k=0,1,\dots,N-1 X[k]=Xe[k]+e−jN2πkXo[k],k=0,1,…,N−1
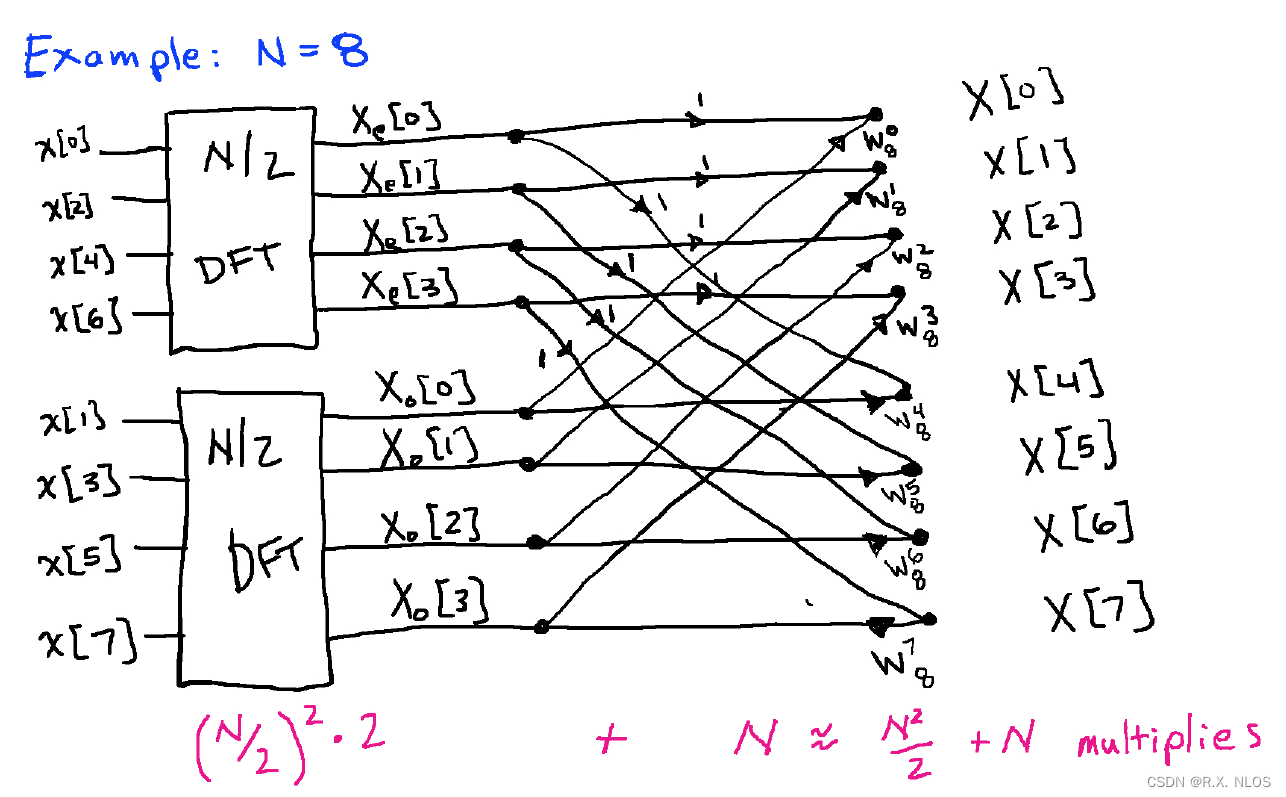
Fast Fourier Transform (FFT) Algorithm
3. 研究现状
3.1 基于FFT的算法优化
近年来,基于 快速傅里叶变换 的算法优化得到了广泛研究。这些优化方法包括 混合基数算法 、 蝶形算法优化 和 并行计算策略 等。这些优化方法在提高计算效率、降低计算复杂度和减小计算误差方面取得了显著成果。
3.2 FFT在实际应用中的发展
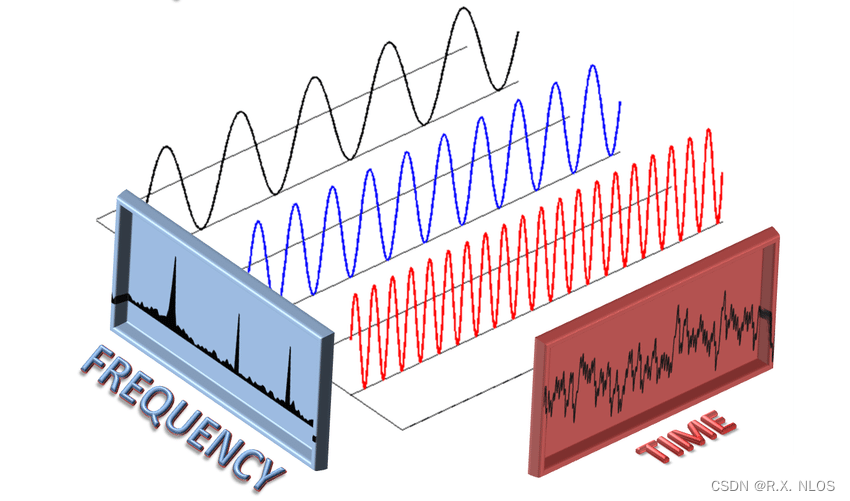
快速傅里叶变换 在许多领域取得了广泛的应用,如信号处理、图像处理、通信、计算机科学等。在这些领域中,FFT已经成为解决实际问题的重要工具。例如,在信号处理中,FFT可以用于滤波、信号分析等;在图像处理中,FFT可以用于图像压缩、去噪等;在通信领域,FFT被用于调制解调、信道估计等;在计算机科学中,FFT用于计算卷积和相关性等。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1VChTmzl-1687153654123)(null)]
4. 挑战
尽管 快速傅里叶变换 在理论和实际应用中取得了显著的成果,但仍然面临着一些挑战:
-
算法优化:尽管已有许多算法优化方法,但仍有进一步提高计算效率和降低计算复杂度的空间。
-
实际应用中的问题:在某些实际应用场景中,信号可能具有非线性、非平稳等特性,这些特性可能导致FFT的计算结果出现偏差。
-
计算精度问题:由于计算机的有限精度,FFT计算中可能出现舍入误差等问题,影响计算结果的精度。
5. 未来展望
针对上述挑战,未来研究将继续在以下方向展开:
-
算法优化: 设计更高效的算法,降低计算复杂度,提高计算效率。
-
应对实际应用中的问题:针对非线性、非平稳等信号特性,研究更适用于实际应用场景的FFT扩展方法。
-
提高计算精度:研究更精确的数值计算方法,降低舍入误差等问题对计算结果的影响。
-
跨学科研究:加强与其他领域的交叉应用和研究,发掘FFT在新领域的潜在应用。
总之,未来在理论研究、算法优化和实际应用方面,快速傅里叶变换仍具有广阔的发展前景。
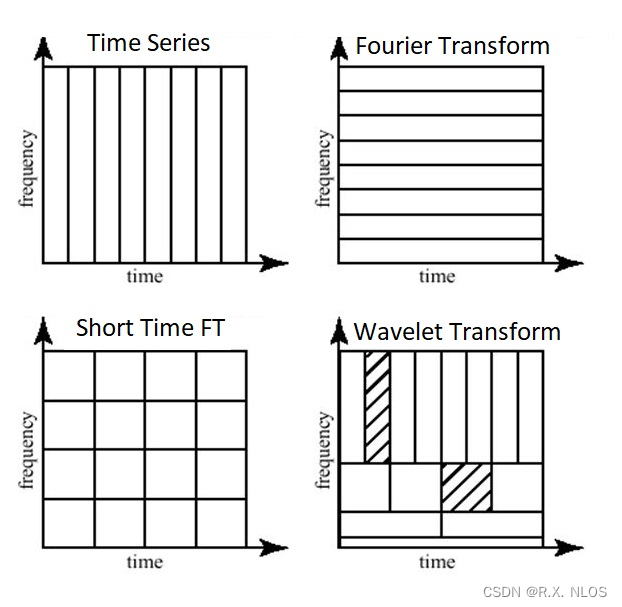
A guide for using the Wavelet Transform in Machine Learning




![[架构之路-215]- 架构 - 概念架构 - 模块(Module)、组件(Component)、包(Package)、对象、函数的区别](https://img-blog.csdnimg.cn/img_convert/3345e7c174187e09b1bec471db9c7726.png)