最近在设计Netflow采集系统时,我想要将客户端的公网IP根据IP库转为对应的国家,此外在CACHE机房中,交换机上是没有AS信息的,因此我们也需要根据IP去查路由库,转换出AS信息。
这两个问题的本质是类似的,无论是IP库还是路由库都是一个网段对应一个数据,因此问题的本质就是根据IP查找出精度最高的网段。很容易就能想到这与路由表的匹配规则几乎是一致的。
对于各个厂商的交换机我在网上很难查到匹配规则时如何实现的,Linux内核也有一套自己的路由匹配逻辑,这可以作为我的参考。
根据之前的学习,我知道路由的方法可以分为两大类:
- 总体设计为树形结构,以IP作为Bucket,不同的网段作为Bucket内的链接节点,可以称为路由地址树。可以辅以路径压缩,Level压缩,Linux内核就是用这种方式实现的。
- 将网段映射成不想交的区间,相交部分以更精确的前缀为准。以这些区间为节点,构建一个区间树,再进行二分查找
只看上面的介绍可能让人一头雾水,接下来我会简单介绍一个两种方法的具体实现
基本数据结构分析
首先我们来想最简单的情况,以IP地址为Key,都有什么方法可以查找到对应的Value呢?有三种基本数据结构可以使用
- 数组:建立一个长度为2^32的数组,优点是查询速度最快,只有O(1),缺点就是太费内存,不是很现实
- 哈希表:优点是节省了内存,同时查询效率也很高,缺点是如果有扩容操作很影响效率
- 树:优点是节省内存,只需要存储有数据的叶子节点。缺点是时间复杂度较高,为logn。对应的树形结构可以参考下图
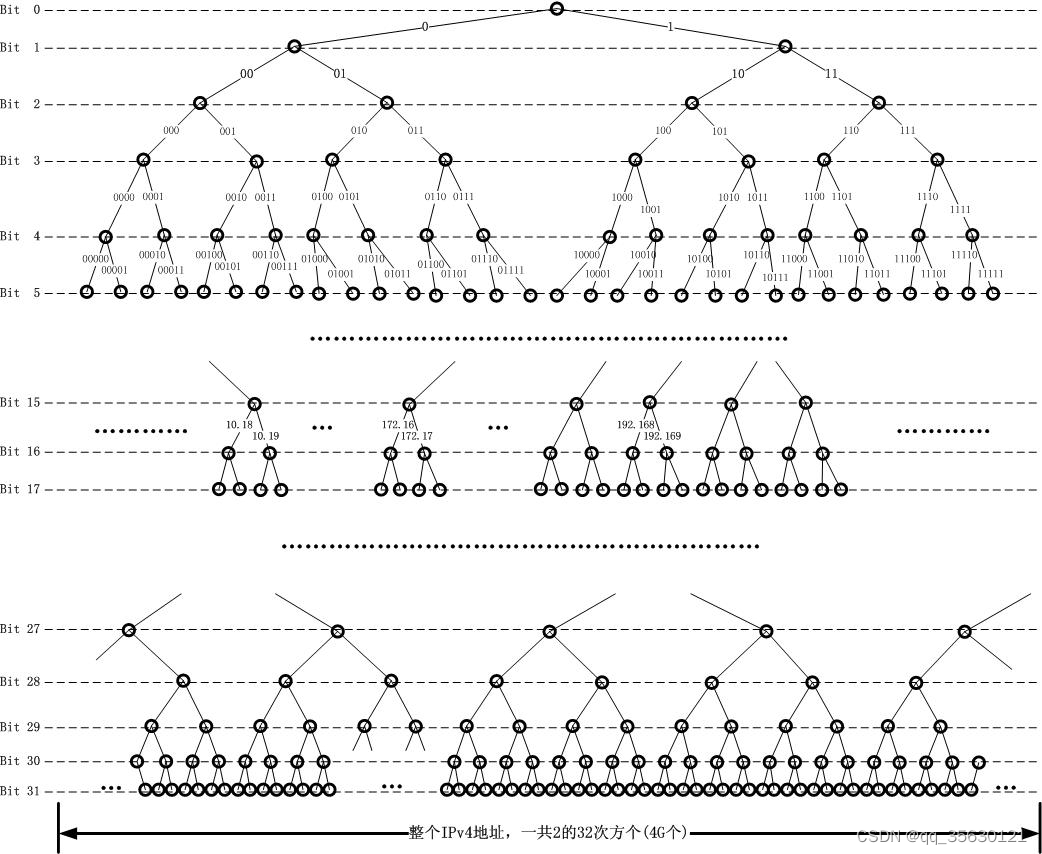
对于这个问题看起来哈希表和二叉树貌似都可以接受,但如果存储的Key不是一个单独的IP,而是一个网段呢?
- 对于数组,我们可以将网段所对应的数据映射到每一个网段所对应的节点中,如果有两个网段同时映射到了一个节点,按照最长前缀匹配规则,节点中只保留最精确的网段。这时可以发现,许多连续的节点都对应着同一个网段,可以将他们合并成一个包含着left和right参数的结构体节点。最终获得的结构体节点数量跟网段的数量在一个数量级,这样的数组反而具有实用价值了。此时的IP已经不再是数组的索引了,但由于区间仍然是按照顺序排列的,可以使用二分查找到对应的区间,时间复杂度为logk,k为网段数量。这一思想就是区间查找的精髓。
- 对于哈希表,上述的合并思想就不再适用了,一个网段有多大就需要有多少个对应的节点,例如我们要存一个16位掩码的网段,就需要2^16个哈希表节点,这显然不是什么好办法。上述查找思路都是先查找IP再查找网段,我们还可以先定位网段大小再定位IP,根据这一思想我们可以创建32个哈希表,分别对应32中长度的网段,再在每个哈希表中以匹配完掩码之后的网段值作为Key。这样在匹配一个IP时,我们可以从32位长的哈希表开始匹配,如果没有匹配上再逐个匹配位数更小的哈希表。这样似乎可以实现一个路由查找的逻辑了,但缺点也很明显,最差情况可能要进行30余次查表,这还是IPV4地址,如果是IPV6那就更惨了,这显然也不是个什么好办法,因此我们可以总结出哈希表不适合做网段匹配。
- 对于树形结构就比较好理解了,一个网段就对应了一个二叉树中的中间节点,在进行匹配时,我们可以记录一个IP经过的所有网段,并以其经过的最后一个网段作为最终匹配的结果。在最差情况下,我们可能仍然需要进行32次匹配,乍一看好像没比哈希表强哪儿去,但实际上并不是这样。首先,一个哈希表查找所花费的时间远远高于匹配一次树形节点,其次只有当当前网段下还存在更细的网段时,才需要进行继续遍历,也就是说并不是所有的IP查找都需要32次匹配,而32个哈希表之前没什么联系,每次都要查询。
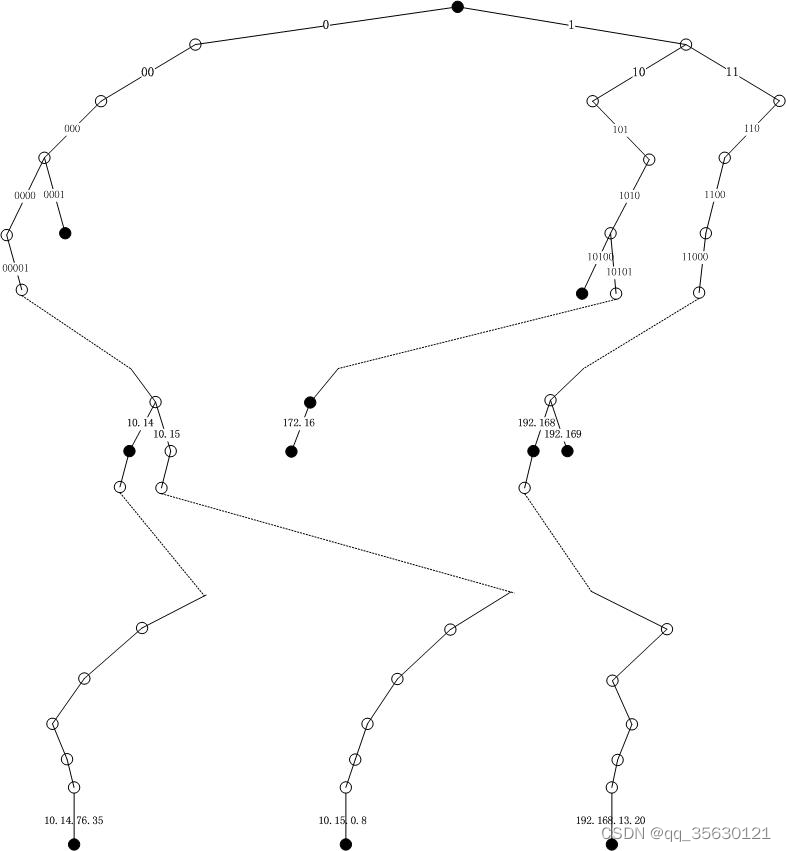
综上所述,数组和树都可以作为网段查询的基础数据结构,二者分别对应了上一节所述的两种方法,即区间查找和路由压缩树查找,实际使用的路由匹配原理也就是这两种思想的进一步优化
区间查询
由于区间查询比较简单,便于理解,我们先行介绍。
举一个简单的例子,我们在路由表中下发如下几个路由,一个0位的默认路由0.0.0.0/0,127.0.0.1/32,8.8.0.0/16,8.8.8.0/25此时对应的区间数组如下图所示:

可以看到四个路由对应着长度为6的数组,每个数组节点是一个区间,各个区间严格升序排列,可以使用二分查找。
上述结构的查询效率已经很快了,但缺点也很明显,就是修改起来很麻烦,这也是数组的通病,假如我们想要删去一个中间的节点,就需要将它之后的所有节点都向前移一位,时间复杂度为O(k),这显然是不能接受的。
优化方法也很容易想到,既然上述结构可以使用二分,就可以转换成一个对应的二叉树:

此时的插入和删除时间复杂度就降到O(1)了
再次基础之上还可以进行优化,由于各个区间能被匹配到的概率是不同的,如果简单的认为IP是均匀分布的,即区间越大匹配到的概率越大,那么可以将区间最大的节点放到根节点,左子树全部小于当前节点,右子树全部大于当前节点。此时的二叉树不再平衡,最坏匹配次数升高,但匹配次数的期望却得以下降:
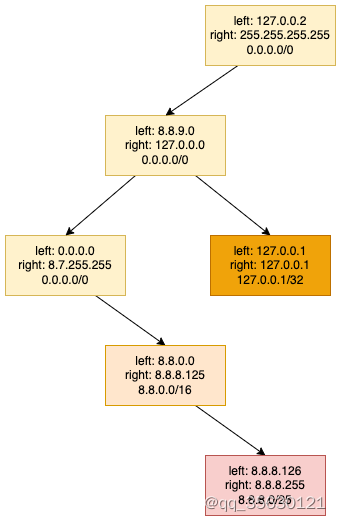
在实际使用中,IP往往并不是均匀分布的,我们可以记录每个区间被匹配到的次数,以该值为权重,动态调整树的形状,这一思想也被用在我们的Netflow采集系统中。
可以看到,上述二叉树的一般节点都是默认路由所对应的区间,如果默认路由走的比较少,我们甚至可以删除全部的默认路由区间,将查找失败区间对应到默认路由,最终二叉树可以优化成如下结构:
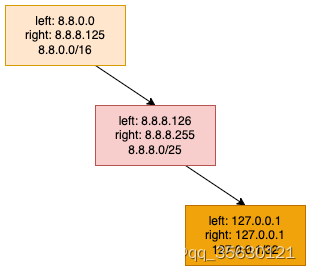
上述就是区间查询的全部内容了,总的来说,区间查询是一种简单易懂,且非常高效的路由查询办法,并且可以根据使用场景进行对应的优化。其时间复杂度为logk,k为路由表项数量。
其缺点就是更新比较复杂,虽然使用二叉树结构已经可以将更新的时间复杂度的理论值降至O(1),但在实际更新中,无论是老区间的删除还是新区间的插入都对会对原来的区间产生影响,极端情况下,插入一个节点就会使节点数量翻一倍(例如在上述例子中插入一个7.0.0.0/8的路由),此时的更新显然不是能简单实现的,同时其时间复杂度也会很高,甚至不能再视作O(1)。
具体的更新操作我也没仔细研究,姑且认为其不能使用在频繁更新的路由表中。
路由压缩树
路由压缩树是对基本的二叉树查找进行的优化,让我们回到二叉树实现的路由表中。
理论上的最大查找深度为32,但很容易发现其实很多节点都是无用的空节点,是可以直接删除的,此时的二叉树可以简化成如下格式:
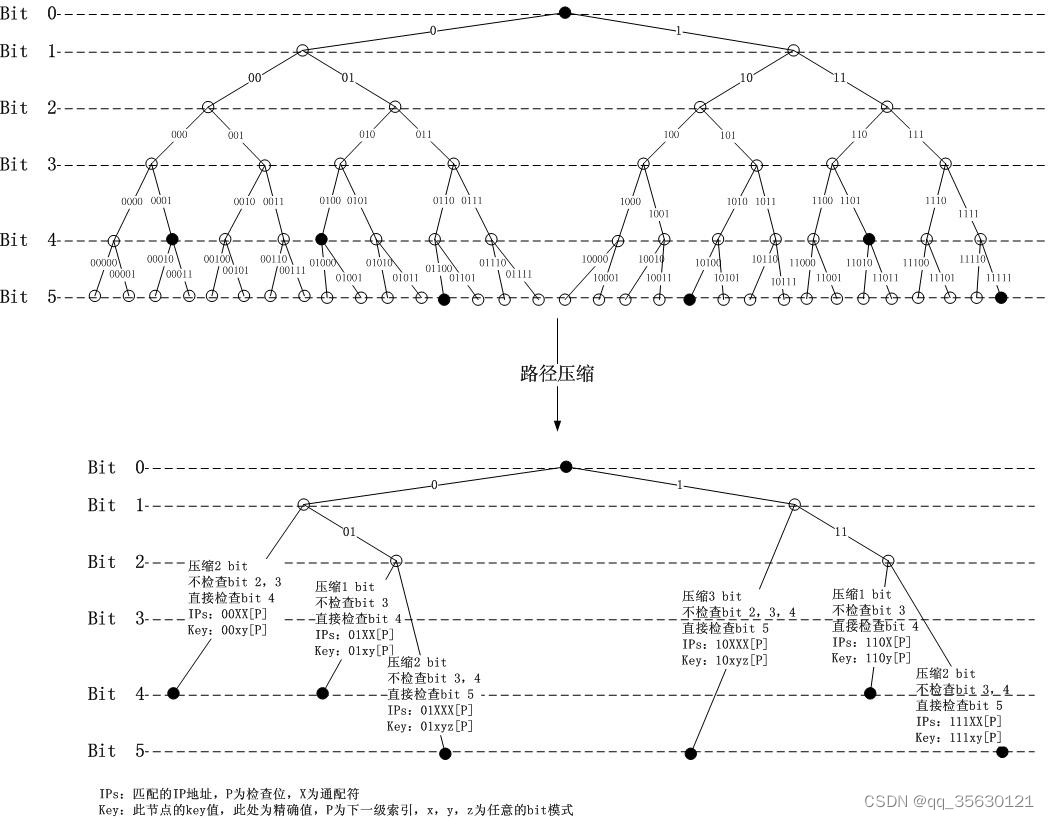
这一过程就称为路径压缩,可以看到,经过路径压缩之后,我们只需要保存二叉树中的包含路由表项的节点以及路由表项的前导节点。
问题
在Netflow采集监控系统中,我们遇到了这样两个问题:
- 一是我们需要根据flow数据中的Client IP解析出对应的国家,这个根据IP库可以实现
- 二是在某些CACHE机房,我们只部署了交换机,而交换机发出的Netflow数据大多是不支持AS字段的,还需要根据ClientIP解析出对应的AS字段,这个可以根据网上的公共路由表实现
不管是我们自己的IP库还是公共路由表,都是一个网段对应一个值,本质上跟路由匹配的原理是一个的,都是已知一个IP,根据最长前缀原则找出其对应的网段
既然问题抽象成了路由匹配,我们就可以调研常见的所有路由匹配算法,从中选取出最适合我们场景的
我们场景的特点有:
- Client IP所属的国家和AS不会经常更换,因此我们几乎不需要更新
- 我们使用的是一台物理机,内存是比较充足的,但为了保证其他进程的使用还是不能太浪费
- 无论是国家还是AS,都有一些经常被匹配到的网段,也就是说每个网段被匹配到的频率差距是很大的
- IP库网段规模在50万,公共路由表规模为100万
常用算法分析
这里只总结各个算法的优缺点,不会进行详细介绍。对于实际使用的各种高级算法,本质上就是时间和空间的权衡,没有绝对的好坏之分,选用哪个需要视具体的情况而定。
哈希查找
查表最容易想到的就是哈希查找了,可以像Linux一开始的那样,为每个网段创建一个哈希表,查找时从32位对应的哈希表开始,从大到小进行哈希查找,查找成功返回,失败进行下一个表的查找
特点
优点:实现起来最简单
缺点:查找很慢,极端情况需要进行32次哈希查找,特别是我们还有IPV6的Client IP,IPV6极端情况甚至要进行128次哈希匹配,有点接受不了
Tire树/字典树
字典树也是一种比较基础的数据结构,由于IP本质上是一个数字,可以按照bit位构建一个最大高度为32(IPV6 128)的二叉字典树,极端情况需要进行32次bit位匹配,效率跟哈希查找相比已经有了很大提高
特点
优点:实现简单
缺点:会有很多中间节点浪费空间,同时查询效率也有很大优化空间
LC-Tire树/压缩字典树
LC(Level-Compress)-Tire树是对字典树的优化,既提升了空间利用率也提升了查询效率。当前Linux路由匹配就是利用这一方法。压缩的目的就是将一颗瘦高的树转换成一颗矮胖的树,删除所有中间的空节点,只保留有路由项和路由项的前置节点。
压缩
压缩共有两种操作,分别是路径压缩和Level压缩,路径压缩负责删除所有的空节点,这些路径上对应的Bit位会在查找时被暂时忽略,路径压缩之后树的高度会大大降低。
Level压缩的本质是将二叉树转为多叉树,此时叶子节点的索引不再是一个Bit位,而是从Pos开始时候的BIt(N)个Bit位,Level压缩之后的二叉树高度会进一步降低。
回溯
由于删除了中间的某些层,在查找时这些层对应的Bit位会被暂时忽略,在查找到叶子节点(也就是有路由项的节点时)才会根据节点的Key精确匹配。由于使用了模糊匹配,最终匹配到的节点有可能是错的,此时就要进行回溯操作。
回溯时会根据最长前缀匹配原则,逐个将叶子节点POS位和之前的Bit位设置为0,继续进行查询
Linux内核中实现了全套的LC-Trie的增删改查,以及树的动态维护算法。
特点
优点:空间利用率很高,在大多数情况下(不回溯的情况)查询也很快,因为树的高度被尽可能压缩。插入和删除操作的实现较为容易,因为只会影响其父节点和子节点
缺点:实现起来过于复杂,几乎没有办法硬件化,因此只有Linux内核使用,各大厂房的路由器都没有使用。同时如果出现回溯会很费时间
Linux的LC-Tire树实现相当复杂,并且因为需要回溯,性能也不是最好,但确实最省内存的做法。由于Linux系统通常不会用来做网络设备,对性能的一些牺牲是值得的。
Radix树/基数树
Radix树应该算作一种算法,或者一种思想,不是一个特定的结构体,Linux使用的LC-Tire树和思科使用的256叉树都可以视为Radix树的特例。
Radix树的基本思想就是提取公共前缀,将公共前缀作为父节点的Key。
256 way mtrie/256叉树
256叉树算是Radix树的一个特例,目前思科在实际的路由器中有使用。256叉树的层数和每层的叶子节点数都是固定的,一共五层,每层用8bit位寻址,每层256个节点。
最少只需要进行四次匹配,在查询到叶子节点之后,会遍历叶子节点的路由项,选出掩码最大的一项。由于256叉树在查找时使用到了所有的bit位,因此他是精确匹配。但是当前叶子节点有可能没有路由,此时需要进行回溯,也就是尝试匹配掩码更少的路由项。
由于256叉树的结构是固定的,所以在初始化时就可以知道当前节点匹配失败时需要匹配的下一个节点,因此其回溯是十分快捷的。
例如,我们当前只有一条路由7.7.4.0/22,对于IP 7.7.7.7,我们首先会查找到7.7.7.7对应的节点,发现没有路由,因此将最低位1置0,跳转到7.7.7.6对应的节点,再次发现没有路由,按照上述逻辑依次遍历7.7.7.4, 7.7.7.0, 7.7.6.0, 7.7.4.0,最终查找到路由
特点
优点:实现较为简单,便于与硬件适配,在路由器中广泛应用。查询效率快,最少需要4次匹配,最多需要36次匹配,更新非常快,因为各个节点之间互不影响。
缺点:占用内存过高,256叉树一共有4G个叶子节点,即使是空的叶子节点也需要保存指向回溯时下一个节点的指针,就按一个节点存两个指针来算(一个指向下一节点,一个指向实际对象地址),一个节点就已经有16bytes了,实际内存就需要大于64G。
DPDK二级树
根据经验和统计数据,实际使用中下发的网段大小通常都是24位以内的,DPDK根据这一现象设计了两级表来实现路由匹配,第一级有224(1600万)个节点,第二级有28(256)个节点,在通常的场景下可以实现使用少量的空间实现最高的查询效率。
同时,为了避免回溯带来的开销,DPDK中保存了两个表,一个rule_table,可以视作路由表,一个lpm_tbl,可以视作转发表。路由表中保存着全量的路由信息,而转发表中则是每个具体的IP对应的优选路由,并且可以保证只一个IP有对应的网段,就一定可以查询到。
除此之外还会有一个路由条目数组,因为一个路由条目可能会被下发到多个转发表项里,为了尽可能的节省空间,转发表里只会保存路由项在其数组内的索引,要想获取最终的路由项还需要进行一次寻址。
转发效率的提升是以空间和路由增删效率为代价换来的。
路由表ADD
所有的路由信息都会被存在一个大数组里,我们可以称其为路由表。路由表按照掩码从地到高的顺序分区域存储当前下发的全量路由信息。还会有另外一个长度为32的数组保存每个网段路由信息在数组中的起始索引和路由数量。
因为路由表的常用操作就是查询,因此使用数组替代链表可以大大提升查询速度。但相对应的是,数组的增删需要移后续的项,增删较慢。因为DPDK是为每个网段划分了一个区域,路由信息在其中的顺序是无所谓的。
因此在增加路由时,只需要从最后一个区域开始,将每个网段区域的首个路由项移动到其末尾,这样就在区域的最前方空出了一个位置。再将前面的区域也依次这样操作,就可以空出要插入的位置。这样插入一个路由项最多只需要进行31次移位(插入掩码为0且所有网段都有路由时)。
路由表DEL
与路由表ADD类似,路由表DEL时会用当前网段最后一个节点覆盖掉要删除的位置,这样在最后就会空出一个位置,在依次用后面区域最后一个节点覆盖掉该位置,就完成了删除。
路由表查询
路由表查询比较简单,首先根据网段查询路由表索引数组,找到对应网段的起始位置和数量,再从该位置遍历路由表数组即可。
转发表ADD
为了删除查询转发表时的回溯操作,转发表在ADD和DEL都直接进行路由优选,因此会做一些额外的操作。
在新增一个网段时,需要遍历所有与其对应的一级表节点,加入我们想下发一个16位网段,那就需要遍历2^8也就是256个节点,查看节点中是否保存了路由项,如果没有则下发当前路由项,如果有的话则会进行比较,最终保存掩码更长的路由项。
如果下发的是比24位更长的路由项,情况会复杂一点,首先会根据路由的前24位Bit获取一级表的索引,如果当前一级表有二级表,会按照与上述类似的操作将路由信息下发到所有对应的节点,如果没有则会申请一个二级表,再进行下发。
转发表DEL
为了保证优选,转发表的DEL最为复杂,因为转发表项只保存了优选后的一条路由,将其删除之后转发表不知道之后的路由该怎么填写,因此需要按照网段从大到小的顺序遍历一次路由表,尝试对当前网段进行匹配,以找到当前的优选路由,这也是一种回溯。
极端情况下没删除一个表项就需要完整的遍历一个路由表(删除的网段没有包含其的上级路由)。
转发表查询
DPDK的转发表查询超级快,首先根据IP的前24位找到一级表对应的位置,首先会查看是否有路由,因为转发表中的路由已经是被优选过的了,因此如果没有路由就是匹配失败,直接返回。
如果有路由的话会检查是否有二级表,如果没有说明没有更精确的网段路由,直接返回当前路由。
如果有二级表则会根据IP的后8位查询二级表,最终返回其中的路由,最多也只需要两次查找。
特点
优点:在常用的网络模型下实现了空间和时间权衡的最优解,同时使用路由表和转发表相分离的操作消除回溯操作,查询效率极快,一般只需要一次匹配,最差也只需要两次匹配。同时也保证了增删效率。
缺点:增删操作在部分极端情况会很慢,例如我们想下发一个0.0.0.0/0的默认路由,就需要遍历全部的1600万个一级表项。同时在下发的路由不满足经典模型(也就是32位网段很多)时会浪费大量内存,因为二级表都是整体申请使用的,我们如果仅仅只下发两个不在同一24位网段下的32位网段就需要耗费2*256长度的数组,极端情况甚至直接不可用。
区间树
将每个路由映射到一个具体的区间,如果有多个路由重叠,那么区间值取精度最高的路由项,最终可以获得一组连续且互不重叠的区间。
按照二分查找的规则可以将这些区间构成一个二叉树。甚至可以根据区间大小做进一步优化,将区间范围较大(或访问频率较高)的节点作为Root节点,然后对左子树和右子树做同样的操作,递归构建查询期望最小的二叉树。
特点
优点:容易构建,空间利用率很高,一般不会超过路由表项的二倍,查询速度特别快,时间复杂度为log(k),根据访问频率优化可进一步提高查询效率
缺点:不易维护,因为一个区间的增删会对其他区间造成影响,不适合频繁修改
总结
综合以上各种算法的优缺点,我们最终选用区间树作为Netflow采集系统中的路由匹配数据结构,因为其实现较为简单,所占空间很少,查询速度非常快,同时我们的IP库又不会经常改变,其缺点也被完美规避。
同时我们还根据各个节点的访问频率对树的结构进行动态调整,具体做法是每个节点记录一天之内被访问到的次数,每天根据这一数据重构树的结构,将访问频率最高的节点置位Root节点。
以IP库举例,共有50万个节点,由于IP库互不重叠,对应的是50万个区间,原始的二分查找匹配次数期望约为18次,但是其中常用的一万个区间就已经能覆盖90%多的查询了,期望可以降低至13,查询效率提升近30%








![[附源码]计算机毕业设计汽配管理系统Springboot程序](https://img-blog.csdnimg.cn/22ad3cd0ec2e49a08e165edb871b83f1.png)