课本：
在这里插入图片描述

考试题型：
题型一、计算题（30分）
1、定点数表示：用原码、反码、补码、移码表示十进制数（5分）
2、浮点数表示：十进制数↔单精度浮点数（5分）
3、加减运算：变形补码（10分）
4、乘除运算：补码一位乘法（Booth算法）、原码加减交替法（不恢复余数法）（10分）
题型二、分析题（25分）
1、Cache和主存映射地址（8分）
2、不同寻址方式下求有效地址和操作数（12分）
3、中断屏蔽字改变中断处理顺序（5分）
题型三、设计题（25分）
1、指令操作码扩展（10分）
2、存储器扩展（20分）
题型四、问答题（15分）
1、主机结构及数据通路

🕒 1. 运算方法与运算器
- 🕘 1.1 定点数表示
- 🕘 1.2 浮点数表示
- 🕘 1.3 加减运算
- 🕘 1.4 乘除运算
🕒 2. 指令系统
- 🕘 2.1 寻址技术
- 🕘 2.2 寻址方式
- 🕘 2.3 扩展操作码
🕒 3. 存储系统
- 🕘 3.1 存储器扩展
- 🕘 3.2 Cache
🕒 4. 程序中断
🕒 5. 中央处理器

🕒 1. 运算方法与运算器

🕘 1.1 定点数表示

在这里插入图片描述

1、将-127用原码、反码、补码、移码表示出来（8位二进制，符号位1位，数值为7位）。
解：十进制数转换成二进制数 $127)_{10}=01111111$
原码：1,111 1111
反码：1,000 0000
补码：1,000 0001
移码：0,000 0001

2、将-128用原码、反码、补码、移码表示出来（8位二进制，符号位1位，数值为7位）。
解：十进制数转换成二进制数 $128)_{10}=10000000$
原码：无
反码：无
补码：1,000 0000
移码：0,000 0000

🕘 1.2 浮点数表示

IEEE 754单精度（32位）浮点数：(-1)^S×(1.M)×2^(E-127)

1、真值－37.25，求32位单精度浮点数（用IEEE754标准表示）。

解答：分别将整数和分数部分转换成二进制数
-37.25 = -100101.01
规格化：-100101.01 = -1.0010101×2⁵
E = e+127 = 5+127 = 132 （二进制为1000 0100）
因为－37.25 是负数，所以 S = 1
尾数M = 0010 101
结果为1 100 0010 0001 0101 0000 0000 0000 0000 = C2150000H

2、浮点机器数 (41360000)₁₆，求真值。给出具体的计算过程。

解答： (41360000)₁₆ = (0100 0001 0011 0110 0000 0000 0000 0000)₂
∵ S = 0 ∴ 该数为正数
∴ E = (1000 0010)₂ = (130)₁₀
∴ 130 - 127 = 3
∴ 1.011011 × 2³ = 1011.011
∴ 真值为(1011.011)₂ = (11.375)₁₀

🕘 1.3 加减运算

双符号位的含义：
00：结果为正数，无溢出；01：结果为正溢出；10：结果为负溢出；11：结果为负数，无溢出

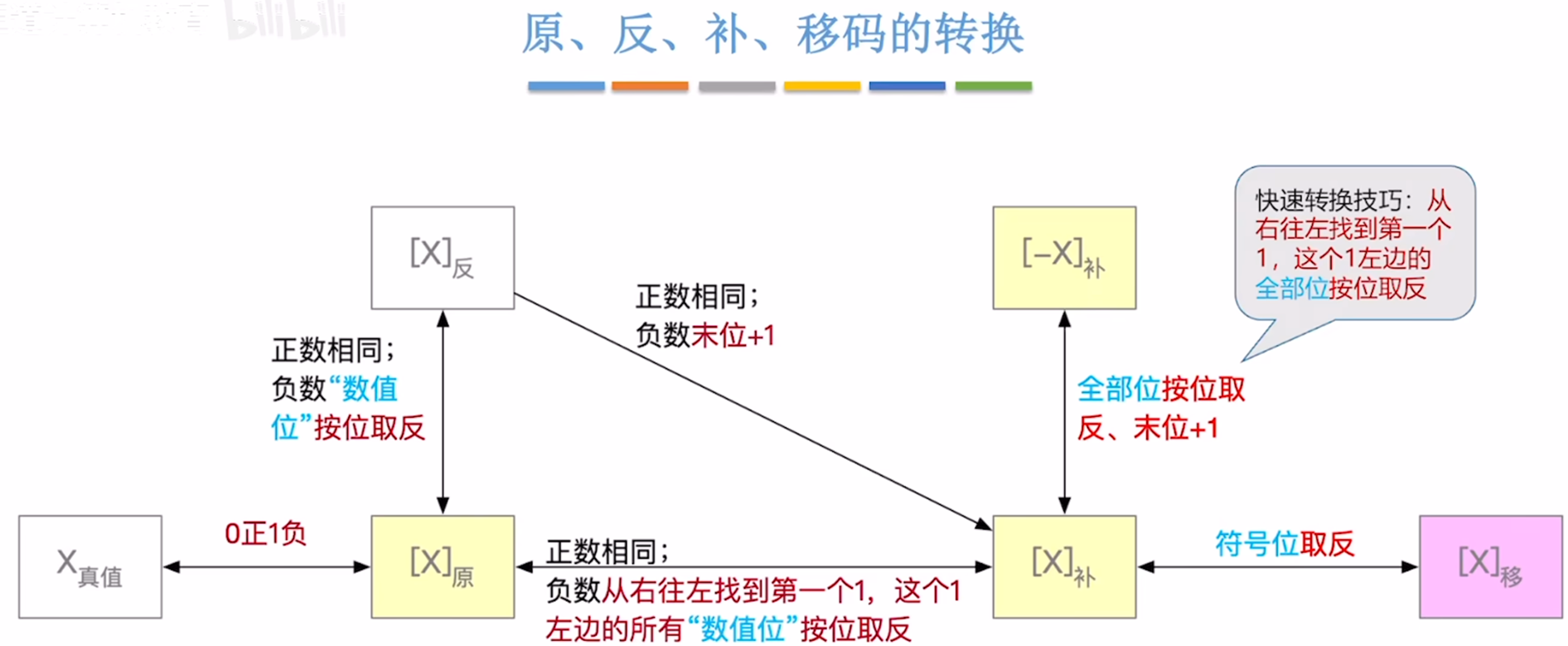
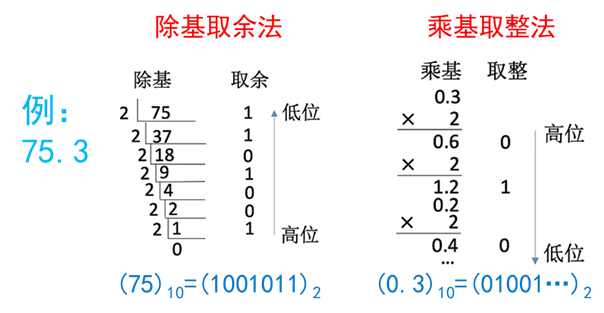
在这里插入图片描述

十进制→二进制的转换：

拼凑法：
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline 2^{12} & 2^{11} & 2^{10} & 2^{9} & 2^{8} & 2^{7} & 2^{6} & 2^{5} & 2^{4} & 2^{3} & 2^{2} & 2^{1} & 2^{0} & 2^{-1} & 2^{-2} & 2^{-3} \\ \hline 4096 & 2048 & 1024 & 512 & 256 & 128 & 64 & 32 & 16 & 8 & 4 & 2 & 1 & 0.5 & 0.25 & 0.125 \\ \hline \end{array}$

Q：分数如何快速转换为二进制？
A：分子转换为二进制，分母转换为 $2^n$ 形式，然后小数点往左移n位，举例： $\frac{11}{32} = - \frac{1011}{2^5} = (0.01011)_2$

1、定点数的运算，设数值位为7 位，x =17/32 , y = 23/32，用变形补码求 x±y ，并判断是否溢出。
（1）写出X、Y的二进制值及其变形补码
（2）写出X+Y的运算过程并判断其结果是否溢出
（3）写出X-Y的运算过程并判断其结果是否溢出

解答：（1）
$(\frac{17}{32}) _{10} =(0.10001)_{2}$
$(\frac{23}{32}) _{10} =(0.10111)_{2}$
$X]_补 = 00.1000100$
$Y]_补 = 00.1011100$
（2） $X+Y]_补 = [X]_补 + [Y]_补 + (00.1000100)_{2} + (00.1011100)_{2} = (01.0100000)_2$
结果为正溢
（3） $Y]_补 = (11.0100100)_2$
$X-Y]_补 = [X]_补 + [-Y]_补 = (00.1000100)_{2} + (11.0100100)_{2} = (11.1101000)_2$
符号位相同，结果为负数，无溢出， $X-Y]_原 = (1.0011000) = (-3/16)_{10}$

2、定点数的运算，设数值位为7 位，A=–65，B=+87，用变形补码求 A±B ，并判断是否溢出。
（1）写出A、B的二进制值及其变形补码
（2）写出A+B的运算过程并判断其结果是否溢出
（3）写出A-B的运算过程并判断其结果是否溢出

解答：（1）
$A = (-65)_{10} = (-100 \ 0001)_2$
$B = (87)_{10} = (+101 \ 0111)_2$
$A]_补 = (11 \ 011 \ 1111)_2$
$B]_补 = (00 \ 101 \ 0111)_2$
（2） $A+B]_补 = [A]_补 + [B]_补 = (11 \ 011 \ 1111)_{2} + (00 \ 101 \ 0111)_{2} = (00 \ 001 \ 0110)_{2} = (+001 \ 0110)_2 = (+22)_{10}$
符号位为00，结果为正数，无溢出
（3） $B]_补 = (11 \ 010 \ 1001)_2$
$A-B]_补 = [A]_补 + [-B]_补 = (11 \ 011 \ 1111)_{2} + (11 \ 010 \ 1001)_{2} = (10 \ 110 \ 1000)_2$
符号位为10，结果发生负溢出

🕘 1.4 乘除运算

Booth算法运算操作：
判断位00：前次部分积右移一位；判断位01：前次部分积加上 $X]_补$ ，将结果右移一位；判断位10：前次部分积加上 $X]_补$ ，将结果右移一位；判断位11：前次部分积右移一位。

注意：原码一位乘法中的右移是逻辑右移，Booth一位乘法中的右移是算术右移，原码加减交替法中的左移是逻辑左移

逻辑移位：无符号数的移位，空出位一律补“0”
算术移位：有符号数的移位

原码的算术移位规则：
不论正数还是负数，在左移或右移时，符号位均不变，空出位一律以“0”补入。

补码的算术移位规则：
正数：符号位不变，不论左移或右移，空出位一律补“0”
负数：符号位不变，左移后的空出补 “0” ，右移后的空出位补 “1” 。

1、已知二进制数 x=﹣0.1011，y=﹣0.1101 ，用补码一位乘法计算x×y的值。

解答：
$x]_补 = 11.0101，[-x]_补 = 00.1011，[y]_补 = 11.0011$

在这里插入图片描述
$\times y]_补 = 00.1000 \ 1111$
∴ $\times y = +0.1000 \ 1111$

2、已知 x = 0.10010，y=﹣0.10101，用Booth算法计算x×y的值。

解答：
$x]_补 = 00.10010，[-x]_补 = 11.01110，[y]_补 = 1.01011$
在这里插入图片描述
$\times y]_补 = 11 \ 10100 \ 00110$
∴ $\times y = - 0.01011 \ 11010$

加减交替法又称不恢复余数法，是对恢复余数除法的改进。
其特点是当某一次求得的差值（余数Ri）为负数时不再恢复余数，而是继续求下一位的商，根据余数的符号作下列处理：
余数为正：商上1，余数左移1位，减去除数
余数为负：商上0，余数左移1位，加上除数

3、已知x=0.1000，y=－0.1010，用原码加减交替法求x÷y。

解答：
$x| = 0.1000，[|x|]_补=00.1000 \ 0000，|y| = 0.1010，[|y|]_补=00.1010，[–|y|]_补=11.0110$

在这里插入图片描述
符号位 $x_s\oplus y_s=0\oplus1=1$ ，所以 $x \div y$ 的商为：－0.1100
因为进行了4次除法，且余数的符号位由被除数决定，余数为： $+0.1000\times 2^{(-4)}$
所以 $\frac{0.1000*2^{(-4)}}{-0.1010}$

注：异或运算相同为0，相异为1

🕒 2. 指令系统

🕘 2.1 寻址技术

☆ 1、设某机的指令字长16位，格式如下，其中X为寻址方式，D为形式地址。取指前，有关寄存器和主存内容如下，请在下表中填入有效地址E及操作数的值。

$\begin{array}{|l|l|l|} \hline \text { OP } & \text { X } & \text { D=100 } \\ \hline \end{array}$ $\begin{array}{|l|} \hline \text { PC=1000 } \\ \hline \end{array}$ $\begin{array}{|l|} \hline \text { Rx=2000 } \\ \hline \end{array}$

在这里插入图片描述

解答：

寻址方式	X	有效地址E	操作数
立即	0	------	100
直接	1	E=D=100	200
间接	2	E=(D)=200	500
相对	3	E=(PC)+D=1102	350
变址	4	E=(R)+D=2100	200
变址间址	5	E=((R)+D)=200	500

相对寻址解析：把程序计数器PC的内容加上指令格式中的形式地址A而形成操作数的有效地址，即EA=(PC)+D，其中D是相对于PC所指地址的位移量，可正可负，补码表示。若当前指令字长=2B，则PC+2。

🕘 2.2 寻址方式

1、根据操作数所在的位置，指出其寻址方式的名称。
(1)操作数在寄存器中。
(2)操作数的地址在通用寄存器中。
(3)操作数在指令中。
(4)操作数的地址在指令中。
(5)操作数地址的地址在指令中。
(6)操作数的地址为寄存器内容与位移量之和（寄存器为基址寄存器，变址寄存器和程序计数器）。

解答：
（1）寄存器直接寻址
（2）寄存器间接寻址
（3）立即寻址
（4）直接寻址
（5）间接寻址
（6）基址寻址、变址寻址和相对寻址

🕘 2.3 扩展操作码

☆ 1、某计算机要求有如下形式的指令：三地址指令4条，单地址指令254条，零地址指令16条，无二地址指令。设指令字长为12位，每个地址码长为3位，试用扩展操作码为其编码。

解（1）三地址：操作码位数=12-3×3=3，4条指令取000~011
（2）一地址：操作码位数=12-3=9，可编2⁹-4×2⁶条指令，取其前254个，100000000～111111101
（3）0地址：操作码12位，指令16条，前9位剩2个×8（后3位）
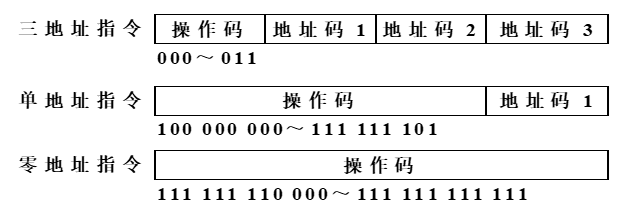
在这里插入图片描述

2、指令字长为12位，每个地址码为3位，采用扩展操作码的方式，设计4条三地址指令、8条二地址指令、180条单地址指令，给出一种操作码的扩展方案。

解：操作码的扩展方案如下
在这里插入图片描述

3、设某指令系统指令字长16位，每个地址码为6位。采用扩展操作码的方式，若要求设计二地址指令15条、一地址指令34条，要求详细写出设计和计算过程：
（1）设计出二地址、一地址指令的格式
（2）计算出最多还可设计多少条零地址指令？

解：
（1）二地址：操作码位数=16-6×2=4，15条指令取0000~1110
一地址：操作码位数=16-6=10，可编2¹⁰-15×2⁶条指令，取其前34个，11110 00000 ~ 11111 00001
在这里插入图片描述
（2）二地址指令剩余的码点状态：2⁴-15=1 种
一地址指令剩余的码点状态：1×2⁶-34=30 种
则还可以设计30×2⁶=1920条零地址指令。

4、某机器为定长指令字结构，指令字长为16位，每个地址码为4位，采用扩展操作码的方式，设计15条三地址指令、15条二地址指令、15条单地址指令，给出一种操作码的扩展方案。

解：设用XXXX表示一个地址码，操作码的扩展方案如下
三地址指令：0000 XXXX XXXX XXXX~1110 XXXX XXXX XXXX（15条）
二地址指令：1111 0000 XXXX XXXX~1111 1110 XXXX XXXX（15条）
单地址指令：1111 1111 0000 XXXX~1111 1111 1110 XXXX（15条）

5、某机指令字长为12位，每个地址码为3位，试给出一种操作码的扩展方案，使该机指令系统能有6条三地址指令、8条二地址指令和16条单地址指令。

解：设用XXX表示一个地址码，操作码的扩展方案如下
三地址指令：000 XXX XXX XXX~101 XXX XXX XXX（6条）
二地址指令：110 000 XXX XXX~110 111 XXXX XXXX（8条）
单地址指令：111 000 000 XXX~111 001 111 XXX（16条）

🕒 3. 存储系统

🕘 3.1 存储器扩展

☆ 1、用1K×4位的DRAM芯片构成4K×8位的存储器。
（1）存储器扩展采用的是哪种扩展方式？
（2）画出该存储器组成的逻辑框图。
（3）采用异步刷新方式，如最大刷新间隔为2ms，则相邻两行之间的刷新间隔是多少？

解：（1）用1K×4位的DRAM芯片8片，采用的是字和位同时扩展。
（2）逻辑框图
在这里插入图片描述
手绘版：

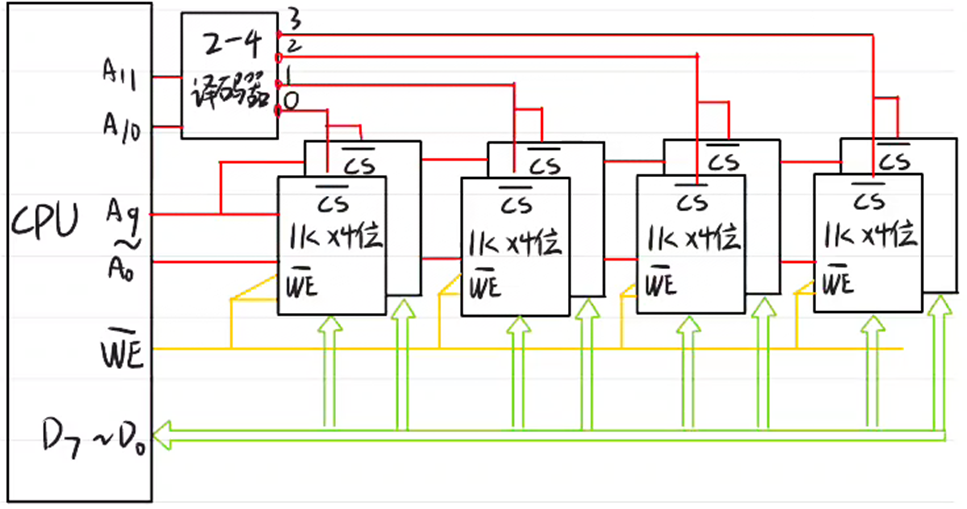
（3）每一个芯片的容量是 $2^{\frac{10}{2}} \times 2^{\frac{10}{2}} \times 4 = 2^5 \times 2^5 \times 4$ ，组成32 × 32的矩阵
两次刷新的最大时间间隔=2ms/32=62.5μs

2、用8K×8位的DRAM芯片构成32K×16位的存储器。要求：
（1）画出该存储器组成的逻辑框图。
（2）设存储器读写周期均为0.5μs，CPU在1μs内至少访问一次。试问采用那种刷新方式比较合理？两次刷新操作的最大时间间隔是多少？对全部存储单元刷新一遍所需的实际时间是多少？

解：（1）逻辑框图如下：
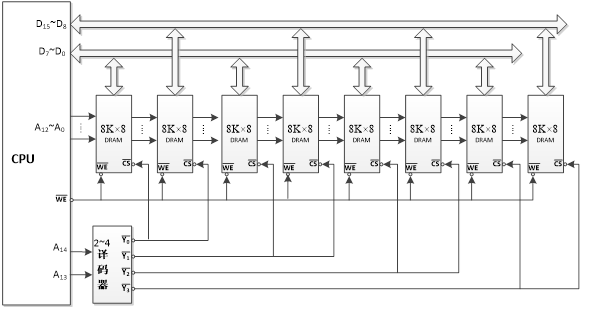
在这里插入图片描述

（2）采用异步刷新方式比较合理
每一个芯片的容量是8K × 8，组成256 × 256的矩阵
两次刷新的最大时间间隔=2ms/256=7.8125μs
对存储器刷新一遍所需的实际时间=0.5μs × 256=128μs

☆ 3、某存储器最小32KB地址空间为系统程序区，与其相邻的16KB地址空间为用户程序区。现有下列存储芯片：32K×1的DRAM、16K×4的DRAM、16K×8的ROM。要求：
（1）通过计算，合理选用上述存储芯片并选择扩展方式。
（2）画出该存储器组成的逻辑框图。
（3）设存储器读写周期均为0.5μs，CPU在1μs内至少访问一次。试问刷新用户程序区采用那种刷新方式比较合理？两次刷新操作的最大时间间隔是多少？对用户程序区全部存储单元刷新一遍所需的实际时间是多少（最大刷新间隔为2ms）？

解：（1）∵ $\frac{32k \times 8 位}{16k \times 8 位} = 2 片$
∴ 系统程序区选用16K×8的ROM芯片2片，采用字扩展；
∵ $\frac{16k \times 8 位}{16k \times 4 位} = 2 片$
∴ 用户程序区选用16K×4的DRAM芯片2片，采用位扩展。
（2）由于地址线条数 $log_2⁡32K$ ，所以地址线条数最少为15条。逻辑框图如下：
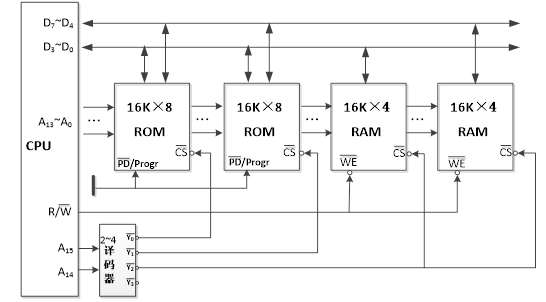
在这里插入图片描述
手绘版：

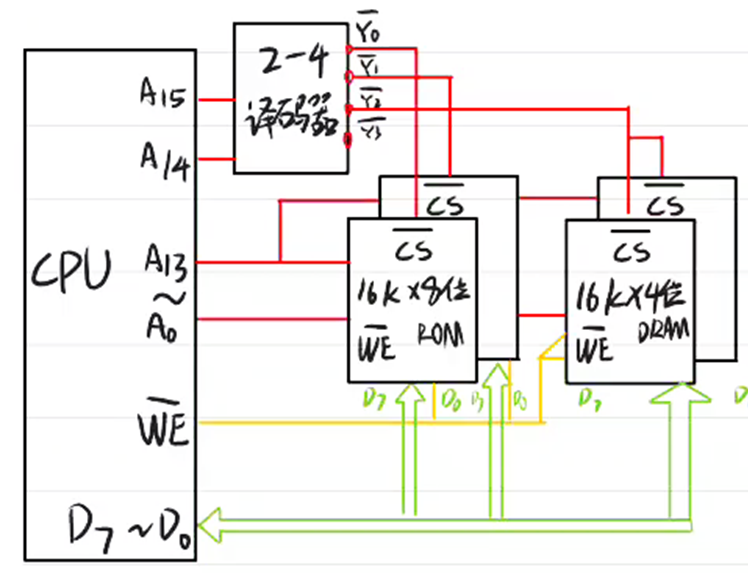
（3）用户程序区采用异步刷新方式比较合理；因为用户区芯片为16K × 4的DRAM，可组成2⁷×2⁷=128×128的矩阵
所以两次刷新的最大时间间隔=2ms/128=15.625μs
3）设两次刷新的最大时间间隔为15.5μs，对存储器刷新一遍所需的实际时间=15.5μs × 128=1984μs

4、某存储器最小8KB地址空间为系统程序区，与其相邻的4KB地址空间为用户程序区。现有下列存储芯片：8K×1的DRAM、4K×4的DRAM、4K×8的ROM。要求：（20分）
（1）通过计算，合理选用上述存储芯片并选择扩展方式。（2分）
（2）画出该存储器组成的逻辑框图。（10分）
（3）设存储器读写周期均为0.5μs，可采用哪几种刷新方式进行刷新？若要求CPU在1μs内至少访问一次，刷新用户程序区采用那种刷新方式比较合理？两次刷新操作的最大时间间隔是多少？对用户程序区全部存储单元刷新一遍所需的实际时间是多少（最大刷新间隔为2ms）?（6分）
解：（1）系统程序区：(8K×8)/(4K×8)=2×1=2片，4K×8的ROM进行字扩展
用户程序区：(4K×8)/(4K×4)=1×2=2片，4K×4的DRAM进行位扩展
（2）逻辑框图如下：
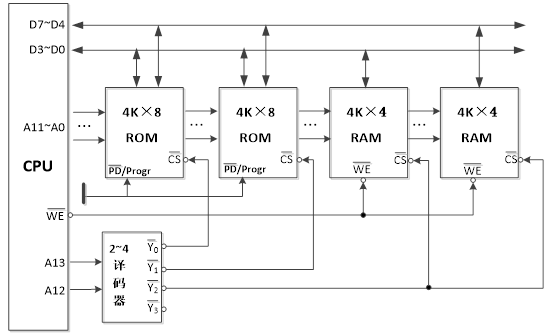
在这里插入图片描述

【解析】：由于地址线条数 $log_2⁡12K$ ，所以地址线条数最少为14条。
由于系统程序区采用的芯片为4K╳8、用户程序区芯片为4K╳4，则地址线为12条，所以高2位作为片选信号。
ROM只能读，所以，控制信号设为0。

（3）可采用集中刷新、分散刷新和异步刷新；采用异步刷新方式比较合理，因为每一个DRAM芯片的容量是4K × 4，组成2⁶×2⁶=64×64的矩阵
所以两次刷新的最大时间间隔：2ms/64=31.25μs
对存储器刷新一遍所需的实际时间：31μs × 64=1984μs（设两次刷新的最大时间间隔为31μs）

☆ 5、设CPU共有16根地址线，8根数据线，并用 $\overline{(MREQ)}$ 作访存控制信号， $R/\overline{W}$ 作读写控制信号，现有下列存储芯片：

RAM：1K×8位、2K×4位、4K×8位
ROM：2K×8位、4K×8位

以及74138译码器和各种门电路（自定），画出CPU与存储器连接图。要求：
（1）最大4K地址空间为系统程序区，与其相邻2K地址空间为用户程序区。
（2）合理选用上述存储芯片，说明各选几片？写出每片存储芯片的地址范围。
（3）详细画出存储体连线图。

解：（1）CPU支持的容量为：2¹⁶×8位=64KB
系统程序区对应的空间：
1111 1111 1111 1111
1111 0000 0000 0000
用户程序区对应的空间：
1110 1111 1111 1111
1110 1000 0000 0000
（2）系统程序区选择两片2K×8位的ROM芯片（字扩展）：
ROM芯片1：
1111 1111 1111 1111
1111 1000 0000 0000
ROM芯片2：
1111 0111 1111 1111
1111 0000 0000 0000
用户程序区选择两片2K×4位的RAM芯片1、2（位扩展）：
1110 1111 1111 1111
1110 1000 0000 0000
（3）存储体连线图
在这里插入图片描述

🕘 3.2 Cache

1、设主存储器容量为512 KB，Cache容量为2 KB，每块为16 B。回答下列问题:
（1）Cache和主存储器分别有多少块?
（2）采用直接映像方式，主存储器的第132块映像到Cache的哪一块?
（3）Cache地址占多少位?
（4）主存储器的地址有几位? 分哪几段? 每段多少位?
解：
（1）主存块数=512KB/16B=2¹⁵块
Cache块数=2KB/16B=128块
（2）因为132 mod 128=4，所以，主存132块映射到Cache的第4块
（3）若按字节编址，Cache地址位数：log₂2k = 11位
（4）若采用直接映像方式，主存储器共log₂512k = 19位，格式为：

$\begin{array}{|l|l|l|} \hline \text { 区地址（8位） } & \text { 块地址（7位） } & \text { 块内偏移（4位） } \\ \hline \end{array}$

🕒 4. 程序中断

1、简述程序中断方式的基本过程？
答：大体上可以把中断全过程分为5个阶段：
①中断请求：由中断源向CPU发出中断请求信号
②中断判优：通过硬或软件方式将多个中断源按优先级顺序进行排队
③中断响应：CPU同意优先级最高的中断源的中断请求，保护现场
④中断处理：CPU暂停现行程序的执行，转去执行中断服务程序
⑤中断返回：中断服务程序执行完后，恢复现场，返回之前执行的程序。

☆ 2、设某机有5级中断：L0，L1，L2，L3，L4，其中断响应优先次序为：L0最高，L1次之，L4最低。试问：

（1）现在要求将中断处理次序改为L1→L3→L0→L4→L2，各级中断处理程序的各级中断屏蔽值（0”表示允许中断， “1”表示中断屏蔽）如何设置？

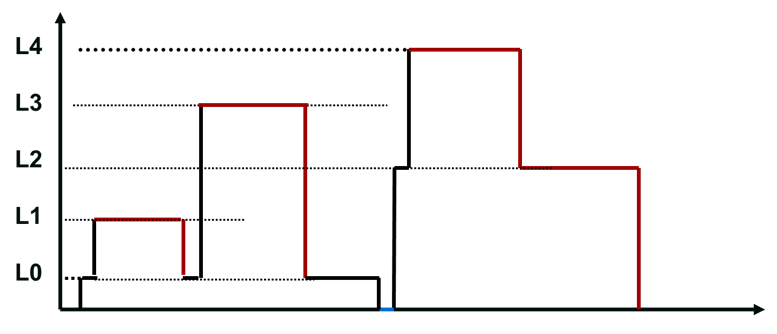
（2）若这5级中断同时都发出中断请求，按更改后的次序画出进入各中断处理程序的过程示意图。

解答：（1）
在这里插入图片描述
（2）

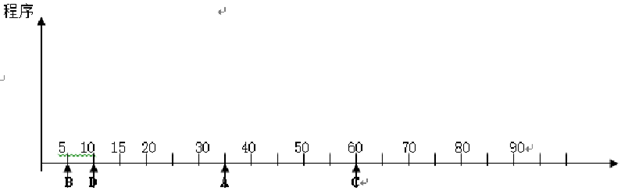
3、现有A、B、C、D四个中断源，其优先级由高向低按A、B、C、D顺序排列，而处理优先级则由高向低按D、B、A、C顺序排列，若中断服务程序的执行时间为20ms，请根据下图所示时间轴给出的中断源请求中断的时刻，画出CPU执行程序的轨迹。
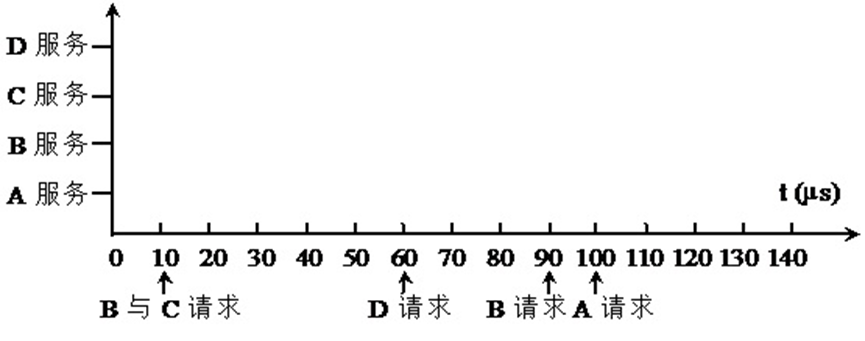
在这里插入图片描述
解答：

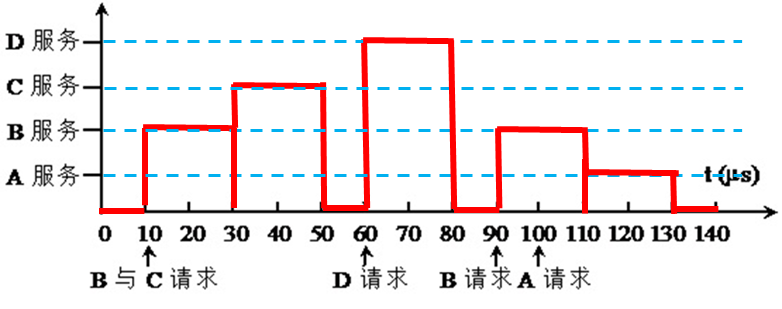
4、设某机有4个中断源，其硬件排队优先次序按1→2→3→4降序排列，各中断源的服务程序中所对应的屏蔽字如表所示：
（1）给出上述4个中断源的中断处理次序。
（2）若4个中断源同时有中断请求，画出CPU执行程序的轨迹。
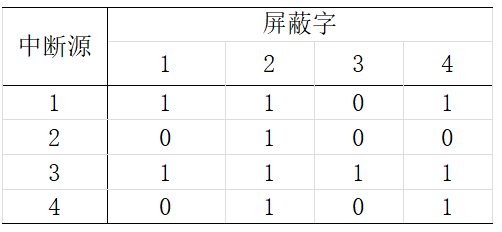
在这里插入图片描述

（1）根据表，4个中断源的处理次序是3→1→4→2
（2）当4个中断源同时有中断请求时，CPU执行程序的轨迹：

解答：（1）3→1→4→2
（2）由于硬件排队的优先次序是1→2→3→4，则CPU先响应1的请求，执行1。 1程序中设置了屏蔽字1101，则开中断指令后转去执行3，3执行完后返回1。1执行完后，2、4同时有请求，根据硬件排队次序，先执行2，2在开中断指令执行之后，转去执行4，4执行完后执行2，直至该程序执行结束。
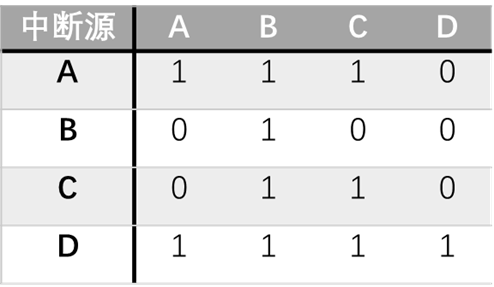
在这里插入图片描述

5、设某机有4个中断源A、B、C、D，其硬件排队优先次序为A>B>C>D，现要求将中断处理次序改为D>A>C>B。
（1）写出每个中断源对应的屏蔽字
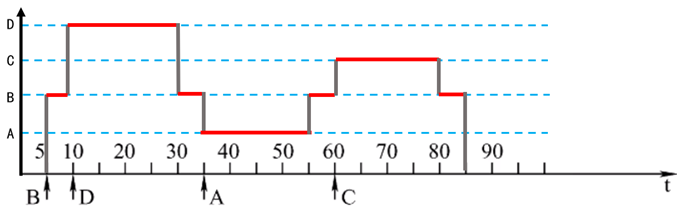
（2）按图时间轴给出的四个中断源的请求时刻，画出CPU执行程序的轨迹。设每个中断源的中断服务程序时间均为20us。
在这里插入图片描述

解答：（1）
在这里插入图片描述
（2）

🕒 5. 中央处理器

☆ 1、（1）画出主机（CPU和主存）的逻辑框图（要求画到寄存器级）。
（2）CPU 中专用寄存器有哪几个,各自的功能是什么?
（3）若存储器容量为64K×32位，指出图中各寄存器的位数。

解答：
（1）
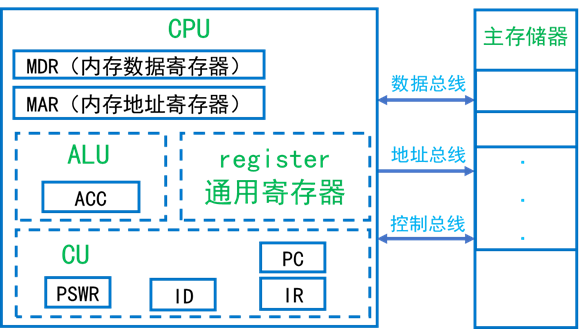
在这里插入图片描述
（2）
①.指令寄存器IR：用来存放当前计算机正在执行的指令
②.程序计数器PC：用来存放下一条要指行指令的地址,或存放计算操作数的地址的基准内容。
③.程序状态字寄存器(PSWR)：用来存放程序状态字。
④.存储器地址寄存据(MAR)：用来保存当前CPU 所访问的主存储器单元地址。
⑤.存储器数据寄存器(MDR)：用来存放由主存储器读出的一条指令或一个数据字；或者存放写入存储器的一条指令或一个数据字时。

（3）
$\begin{array}{|c|c|c|c|c|c|} \hline \text { IR } & \text { PC } & \text { MAR } & \text { MDR } & \text { PSWR } & \text { ACC } \\ \hline 32 & 16 & 16 & 32 & \text { 不确定 } & 32 \\ \hline \end{array}$

2、CPU结构如下图所示，其中有一个累加寄存器AC，一个状态条件寄存器和其他4个寄存器，各部分之间的连线表示数据通路，箭头表示信息传送方向。
（1）标明图中a,b,c,d这四个寄存器的名称
（2）简述指令从主存取出指令到产生控制信号的数据通路
（3）简述数据在运算器和主存之间进行存/取访问的数据通路

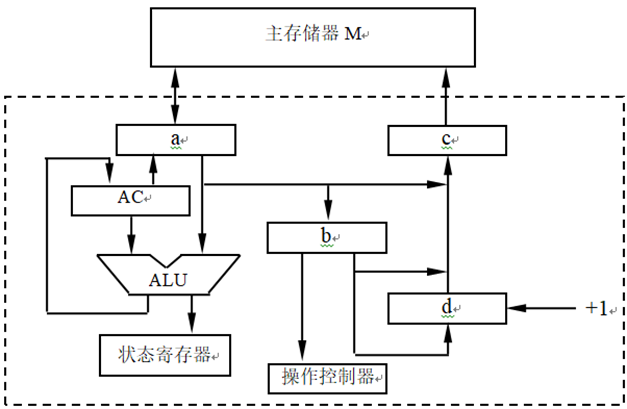
在这里插入图片描述
解：（1）a为MDR，b为IR，c为MAR，d为PC
（2）取指令的数据通路：
PC → MAR → MM → MDR → IR
（3）数据在运算器和主存之间进行存取访问的数据通路
运算器向主存读：M(MAR) → MDR→ ALU→AC
运算器向主存写：AC→MDR→M(MAR)

☆ 3、CPU结构如图示，其中包括一个累加寄存器AC、一个状态寄存器和其他四个寄存器，各部分之间的连线表示数据通路，箭头表示信息传送方向。
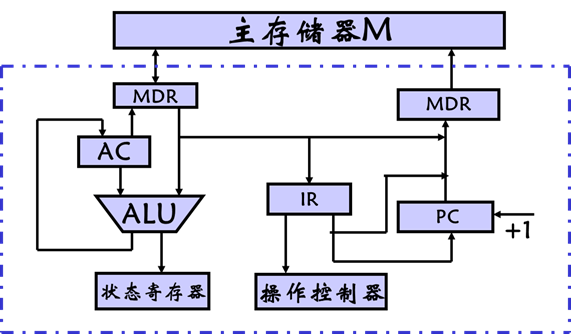
在这里插入图片描述
（1）标明图中四个寄存器的名称。
（2）简述取指令的数据通路。
（3）简述完成指令LDA X的数据通路（X为内存地址，LDA功能为（X）→AC。
（4）简述完成指令ADD Y的数据通路（Y为内存地址，ADD功能为（AC）+（Y）→AC。
（5）简述完成指令STA Z的数据通路（Z为内存地址，STA功能为（AC）→Z。