【状态估计】粒子滤波器、Σ点滤波器和扩展/线性卡尔曼滤波器研究（Matlab代码实现）

news2024/11/26 15:26:13

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 扩展卡尔曼滤波

2.2 线性卡尔曼滤波

2.3 粒子滤波

2.4 Σ点滤波器

🎉3 参考文献

🌈4 Matlab代码及详细讲解

💥1 概述

粒子过滤器通常需要大量粒子，这可能需要大量的运行时间。即使是最简单的粒子过滤器也使用 1000 个粒子的情况并不少见，每次测量需要 1000 次模拟。随着状态维度的增长，必要数量的粒子变得巨大。（我们的问题会从1000个粒子中受益匪浅，但要理解具有如此大量粒子的图会更难。
将不确定性表示为一组粒子和权重（离散概率分布）意味着状态的最佳估计通常非常粗糙，因此粒子过滤器对于需要高精度的问题效果不佳。
当需要更好的性能时，粒子滤波器通常必须进行大量定制，以适应每个单独的状态估计问题，这可能需要很长时间，尤其是因为测试需要运行过滤器，而过滤器本身可能需要很长时间。出于同样的原因，很难找到有用的通用粒子过滤器，尽管自举过滤器可以解决简单的问题。

在Σ点滤波器（也称为无迹滤波器）中，我们不用一大堆散射粒子来表示不确定性，而是假设不确定性具有高斯（正态）分布，并且以当前最佳估计值为中心：

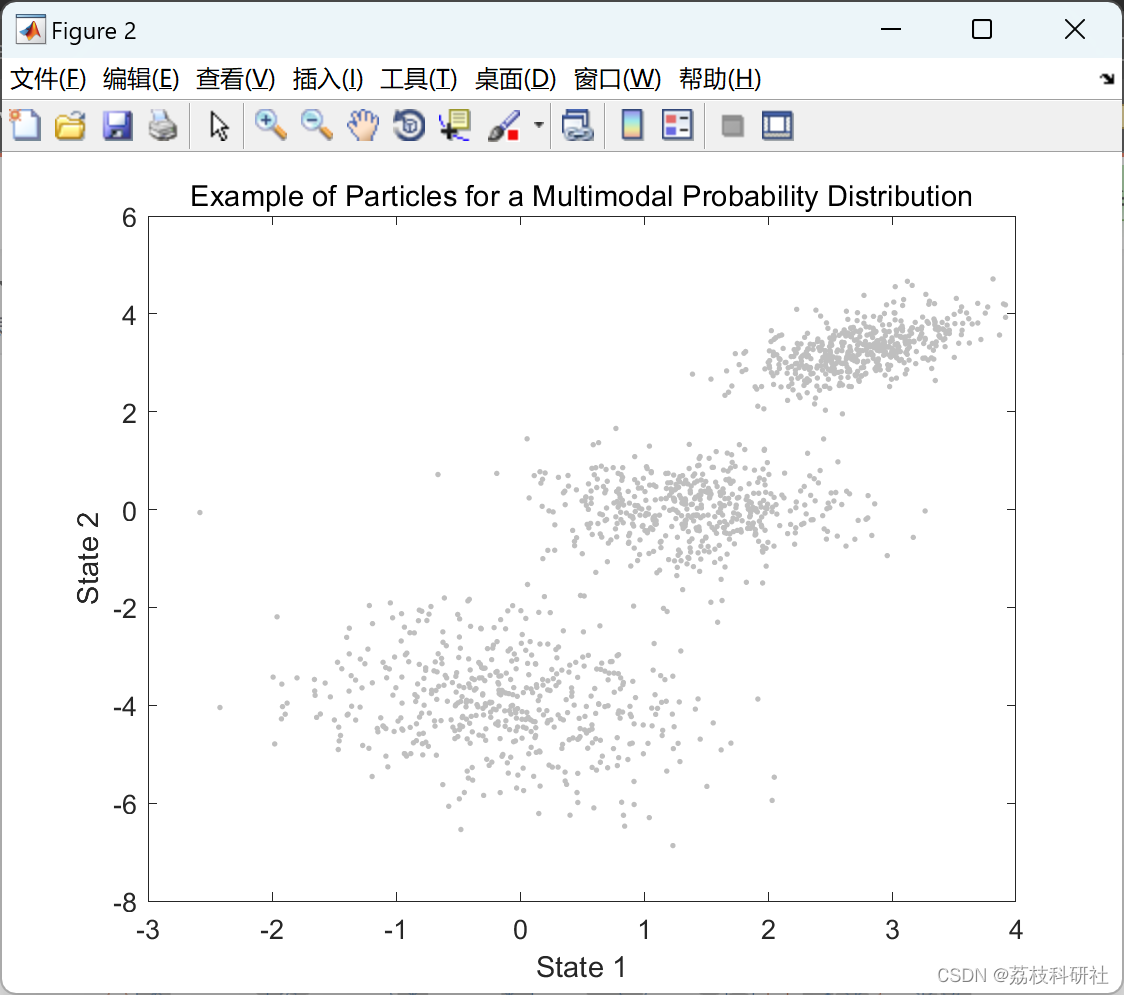
因此，我们可以用协方差矩阵来表示不确定性，就像我们为上面的粒子计算的那样。我们将协方差可视化为围绕状态估计的椭圆，其中椭圆绘制在 3σ 边界处（因此，真实状态大约 99.7% 的时间在这个椭圆内）。绘制 1000 个粒子只是为了进行比较。

当各种不确定度源（先前的不确定度、过程噪声和测量噪声）是单峰且不相关的时，Σ点滤波器是一个强大的选择。一些优点：

在他们的假设中，它们通常比粒子过滤器更准确，因为它们不依赖于随机粒子。
它们比粒子过滤器快得多。粒子过滤器可能需要 1000 个点，而 Σ-point 过滤器可能只需要 9 个左右。
他们的假设适用于许多不同的实际问题，并且设置Σ点滤波器只需要定义传播函数，测量函数，过程噪声协方差和测量噪声协方差，所有这些都是粒子滤波器所必需的。
Σ点滤波器有标准形式，因此在书籍或期刊中找到良好的参考相对容易。

不过，我们可以列出一些缺点。

奇怪的问题可能导致Σ点滤波器“分崩离析”。例如，在我们的球问题中，如果时间步长更大，那么在一次或两次反弹中，sigma 点将变得非常“混乱”，并可能导致样本协方差矩阵毫无意义。可能很难避免这种情况，而粒子过滤器不会有这个问题。
虽然它们比粒子滤波器快得多，但它们也比扩展卡尔曼滤波器慢得多，我们稍后会谈到。

📚2 运行结果

2.1 扩展卡尔曼滤波

2.2 线性卡尔曼滤波

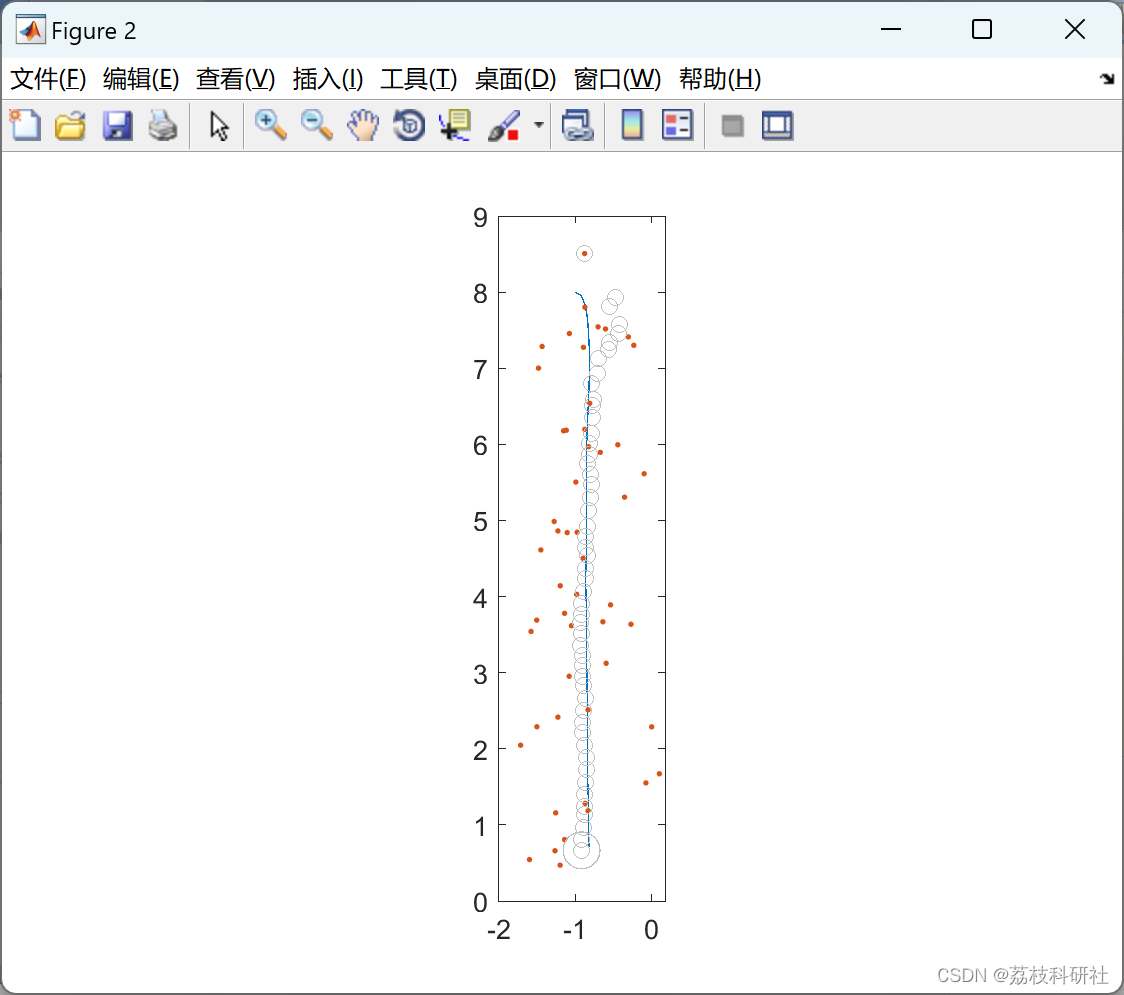
2.3 粒子滤波

2.4 Σ点滤波器

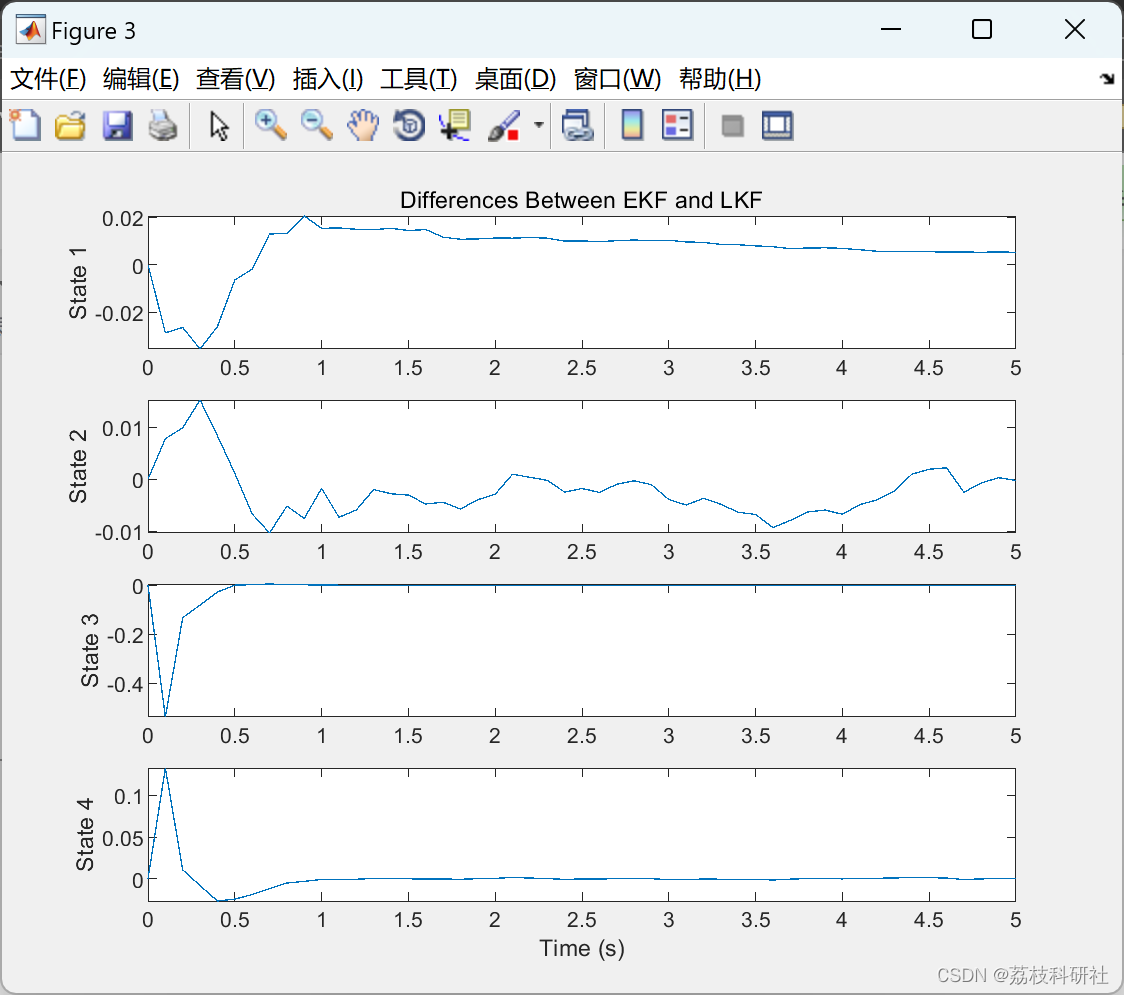
部分代码：

%% Create the true system and show the initial filter state.

% Set the random number generator seed so the results are the same every
% time we run the script. (Comment out this line to see different results
% every time.)
rng(1);

% Initial true state, measurement noise covariance, and measurement
x0 = [0; 3; 1; 0];
R = 0.5^2 * eye(2);
z0 = x0(1:2) + covdraw(R);

% Initial state estimate and covariance
xh0 = [z0; 1; 0];
P0 = blkdiag(R, 2^2 * eye(2));

% Calculate the whole true trajectory.
[~, x, t] = propagate_ball(0, 10, x0);

% Prepare the figure.
set(clf(figure(1)), 'Color', [1 1 1]);
axis equal;
axis([-1 11 0 5]);
xlabel('x [m]');
ylabel('y [m]');
hold on;

% Draw the 3-sigma boundary for the uncertainty.
ell = ellipse(P0, xh0);
hP = plot(ell(1,:), ell(2,:), 'Color', 0.75 * [1 1 1]);

% Add particles for comparison only.
X = bsxfun(@plus, covdraw(P0, 1000), xh0);
hX = plot(X(1,:), X(2,:), '.', 'Color', 0.75 * [1 1 1]);