简介

或许你有一个疑问：为什么堆排序使用二叉树，但是叫堆排序，而不是树排序？
因为堆排序的前身正是叫做树选择排序（Tree Selection Sorting），使用树结构，但是要稍微简单一些。

高德纳（Donald E. Knuth）先生形容树选择排序算法像兵乓球比赛，所以这里使用一下 TAOCP 中的例子。假设有八个人参加比赛，需要评判出第一名到第八名，赛程如下：

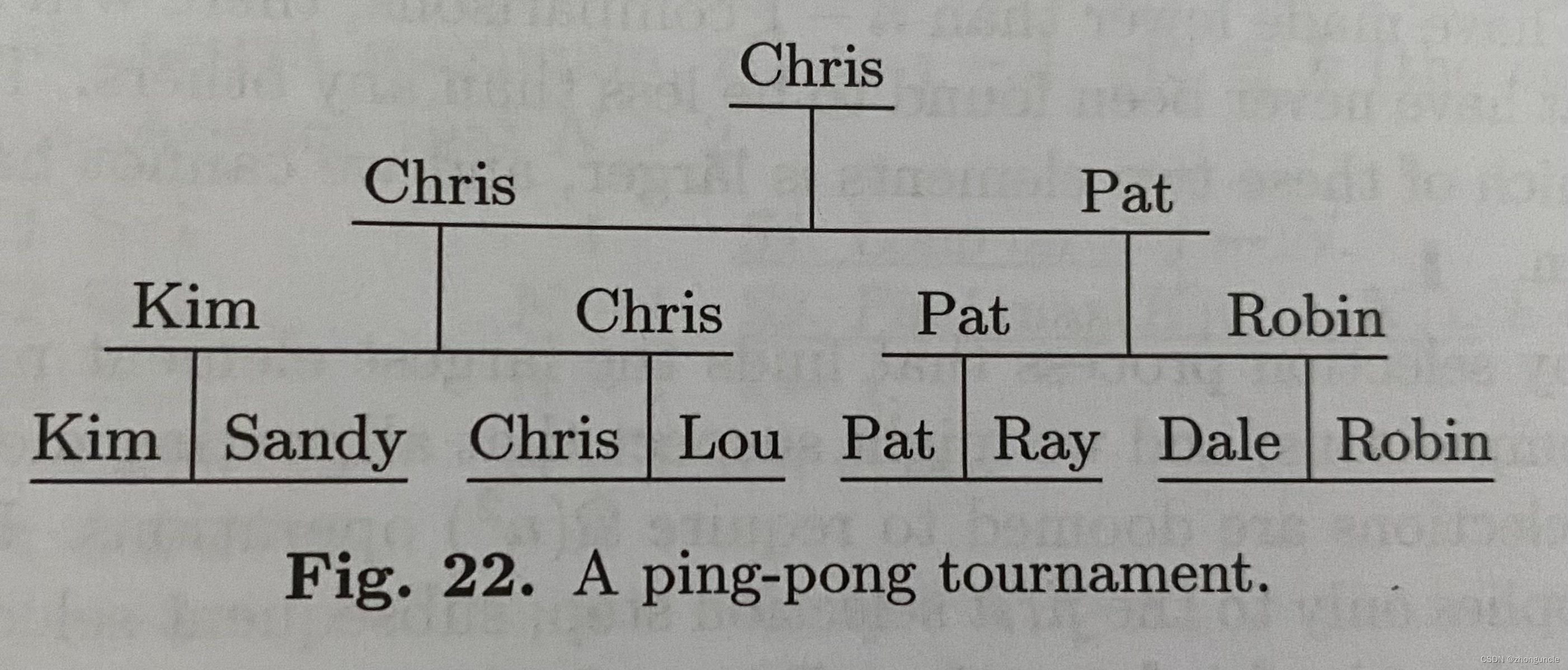
Kim 和 Sandy、Chris 和 Lou、Pat 和 Ray、Dale 和 Robin分组比赛，胜者晋级。可以看到在 7 次比赛之后，最后的冠军是 Chris，但是第二名亚军是谁呢？是 Pat 吗？不一定是 Pat，因为 Kim 和 Lou 虽然都输给了冠军 Chris，但是不一定会比 Pat 弱，所以还需要 Kim 和 Lou 进行一场比赛，然后胜者再与 Pat 进行一场比赛（这时候你可能好奇为什么 Sandy 不用和 Pat 比赛，是因为 Sandy 本就弱于 Kim，无论赛况如何，Sandy 永远不可能是第二）。以此类推，最后就可以排序完成了。
那么在这个赛程树中，树根就是冠军，每次选出冠军之后，然后对剩下的人进行重赛（高德纳先生在这里设计为即使运动员生病或状态不佳也得重赛，所以你可能会认为有点不公平哦，但是这里不讨论这个问题）。

算法步骤

树选择排序有两个版本，原始版本和 1962 年 K. E. Iverson 提出的改进版本。

原始版本

原始版本的树排序具体步骤如下，图中叶节点都放最下面方便理解（Procreate 写的字很丑，见谅）：

1. 第一步，对所有叶节点两两对比，选出最小值1，将其输出（也就是从原数组中删除这个元素）；
2. 然后对剩下的元素再进行对比，一个个输出，直到结束。如下图。
   

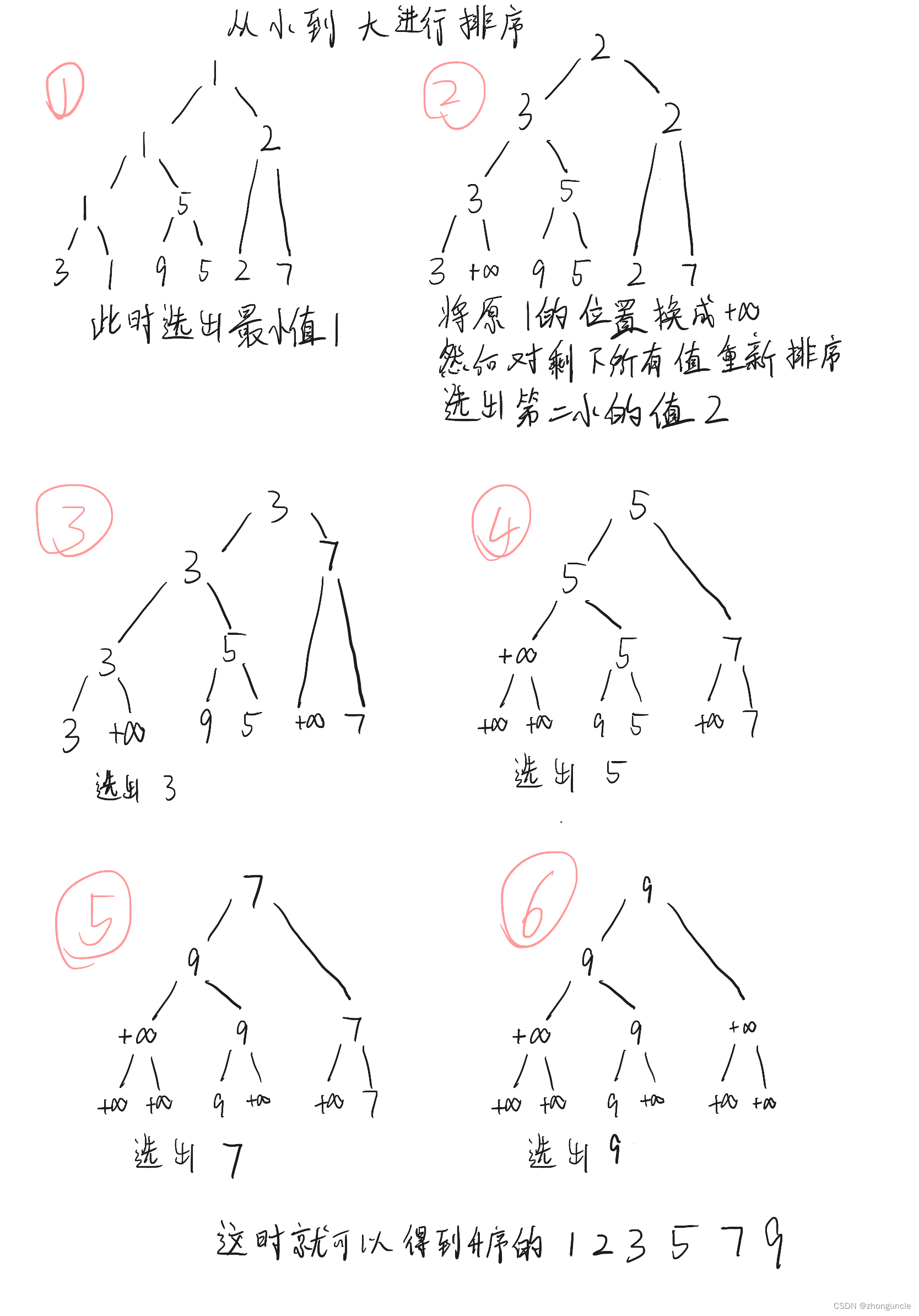
可以看到，这种算法每次在输出选择的最小值之后，就将原本最小值的位置换成$+\infty$，那么要知道每个元素的指针或者下标。（我猜您阅读到这里很好奇$+\infty$怎么在代码中体现出来，这里放到最后细说）
所以树选择排序算法需要的空间分为三部分 N 个关键字、N-1 个指针和存放输出的 N 个位置或指针。不过用数组的格式的话，那就是两个数组即可。

因为每次重新对比只需要改变一条路径（看上图可以看出来），所以选出第二个最小值最多只用$lgN$次（$N$为元素数量），那么对比所有的元素需要$NlgN$。

改进版本

改进版本的树排序使用了“Pater Principle”。个人感觉高德纳先生使用“Pater Principle”一词虽然不是十分精准，但是意思上却十分贴切，而且以我的水平也想不到更好的词了（但是不能说树排序的改进是使用“Pater Principle”发明的，因为树排序的改进是 1962 年，“Pater Principle”是 1968 年）。

彼得原理（Pater Principle）是 Laurence J. Peter 开发的管理概念。Peter 指出，在一个体系中的人们，会上升到能力不符合职称的级别：员工根据他们在以前工作中的成功晋升，直到他们达到不再胜任的水平。

可能有人看上面机翻的解释没有看懂，那么简单来说可以理解成：在一个体系中，如果一个人一直成功晋升，最后会到达一个超过他能力的职位，然后他就不能继续晋升了，但是公司也不会开除他，他就相当于稳定在这个位置了（如果想要更详细的解释可以自己查查，是一个很有意思的原理）。

改进版的树排序就是将叶节点的值进行对比，然后将其放在适当的位置，然后删除之前的节点，这样可以大大降低对比的次数。上面的那个图会变成下面这样：

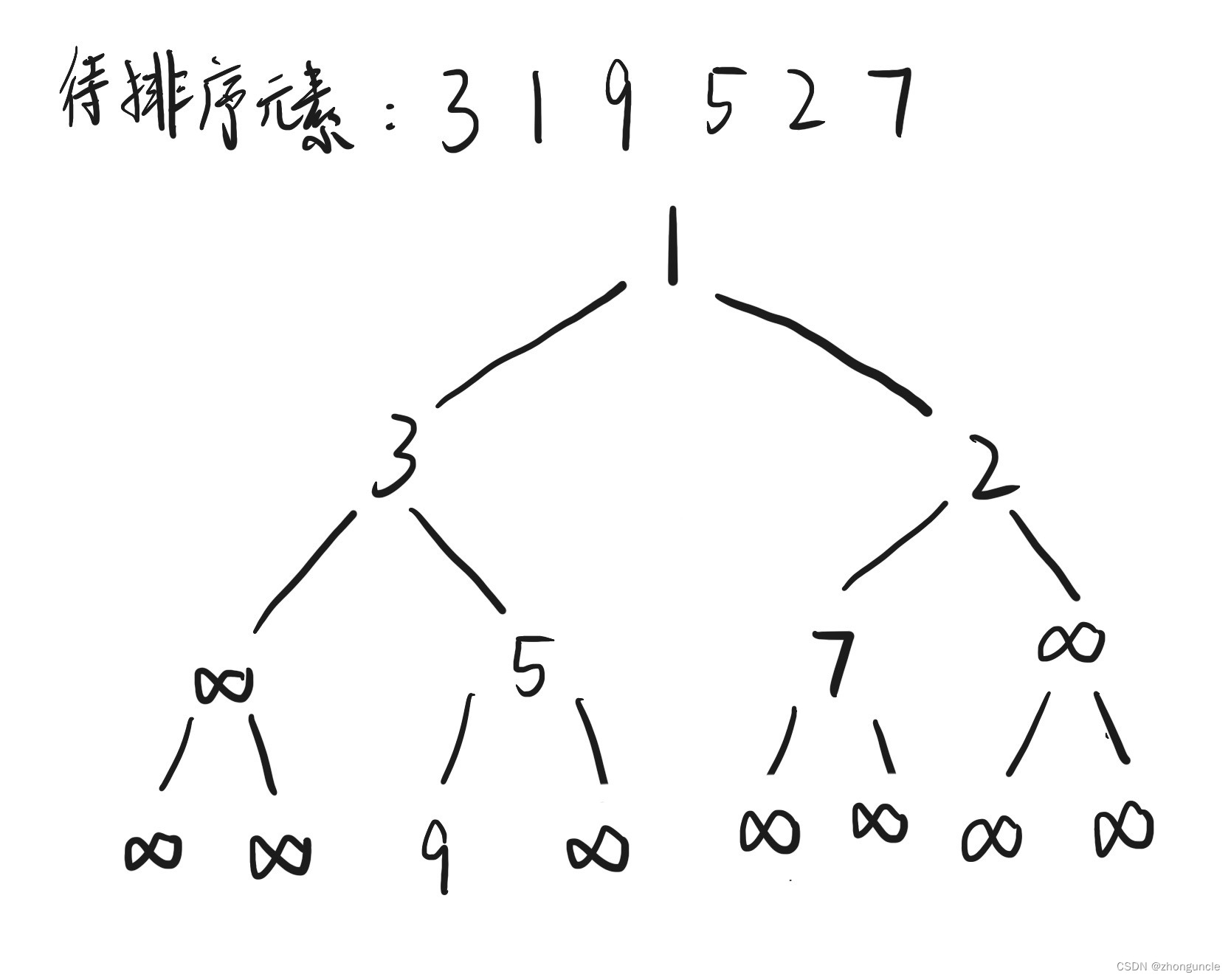
这时候如果忽略$\infty$的话，那么元素顺序应该是1 3 2 5 7 9。如果重复迭代运行改进版本的树选择排序算法，那么你会发现在不断迭代之后，最终二叉树会在两种情况之间“反复横跳”。所以需要想办法改进，这个办法就是堆排序（heapsort）。
或者你可以在第一次树选择排序之后，使用直接选择排序。因为此时元素已经比之前有序许多了，这时候使用不稳定的排序方法会快一些。例如此时只有3和2的位置不对，直接选择会快很多。