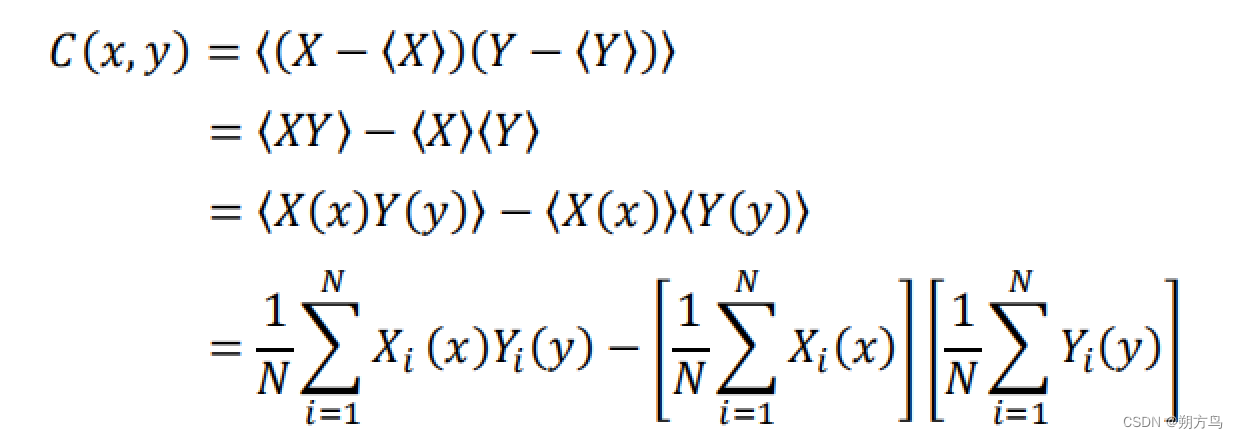目录
一、前言
二、问题背景
三、具体问题
四、解题思路
(一)整体思路
(二)问题一
(三)问题二
(四)问题三
(五)问题四
(六)问题五
五、相关工具及公式
(一)SPSS
(二)指数平滑法
(三)误差分析相关公式
一、前言
本文是对2021 年第十三届 “电工杯” 高校数学建模挑战赛B题:光伏建筑一体化板块指数发展趋势分析及预测 的解题思路,希望能够对正在学习数学建模或者研究该类问题的读者提供帮助。作者在当届的比赛中,依据这个思路获得了本科组二等奖的成绩,可以说这个思路还是具有一定的合理性的。
附获奖证书:

二、问题背景
三、具体问题
四、解题思路
(一)整体思路
需要对光伏建筑一体化板块的走势进行预测,以便了解这一行业未来的发展趋势。由于每支股票的日 K 线和移动平均线指标可以反映出股票的走势,因此可以将它们作为特征变量,建立模型对光伏建筑一体化板块的未来发展趋势进行预测。为此,需要进行以下步骤:
1. 数据预处理:将附件1中的数据进行导入和清洗,包括去除缺失值、异常值等。
2. 特征提取:提取每支股票的日 K 线和移动平均线作为特征变量。
3. 建立模型:根据历史数据,使用机器学习和时间序列分析等方法建立预测模型。
4. 模型验证:使用交叉验证等方法验证模型的准确性和可靠性。
5. 预测结果:根据模型预测结果分析光伏建筑一体化板块未来的发展趋势并给出建议。
(二)问题一
移动平均线模型:
根据附件1,获取光伏建筑一体化板块的日指数数据,并采用带权重的移动平均线模型建模预测该板块的指数走势。然后,绘制5日、10日和20日的移动平均线,以便直观地观察该板块的指数随时间的变化情况。
(三)问题二
模型修正与预测:
使用附件1中的数据来验证移动平均线模型,并对该模型进行修正。然后,使用修正的模型来预测该板块的未来走势。最后,绘制这个板块的未来20个交易日的日移动平均线、三周的周移动平均线和两个月的月移动平均线。
(四)问题三
相关性分析:
在附件1中,获取上证指数和光伏建筑一体化板块指数的日指数数据。通过使用2个月的时间段(从2019年4月1日至2021年5月28日)的日指数数据对这两个指数进行相关性分析,然后研究它们之间的相互关系。
(五)问题四
风险评估和投资方案分析:
利用附件1提供的数据,对光伏建筑一体化板块个股的投资风险进行评估,并根据风险大小对37支股票进行排序。然后,可以根据投资者持有的100万元人民币和每日不超过5支股票的限制,来制定出2021年6月份的最优投资方案。
(六)问题五
撰写行业报告:
首先要详细介绍光伏建筑一体化的定义和发展历史,然后对行业的现状和未来市场发展分析进行详细阐述,并给出该行业未来趋势的建议和预测。最后,可以介绍一些该行业内部的主要参与者、行业的发展瓶颈以及规模扩大所面临的挑战和机遇,以向读者传达有关该行业的整体形象。
五、相关工具及公式
(一)SPSS
SPSS(Statistical Product and Service Solutions)是一种专业的统计软件,主要用于数据分析、数据挖掘、数据建模和预测分析等领域。它提供了各种数据处理、统计分析和报告生成的功能,可以帮助用户在数据处理和分析过程中,发现数据之间的关联性、趋势性和异常情况等,从而支持决策和业务优化。
SPSS的特点在于它拥有非常丰富的统计分析方法,包括描述统计、推论统计、生存分析、因子分析等各种方法,并且提供了直观简单的用户界面,用户可以通过简单的操作完成数据的输入、处理、分析和报告生成等工作。
SPSS广泛应用于市场研究、社会调查、医学研究、心理学、教育研究、政府部门、商业机构等领域。
(二)指数平滑法
指数平滑法是一种常用的时间序列预测方法,其公式如下:
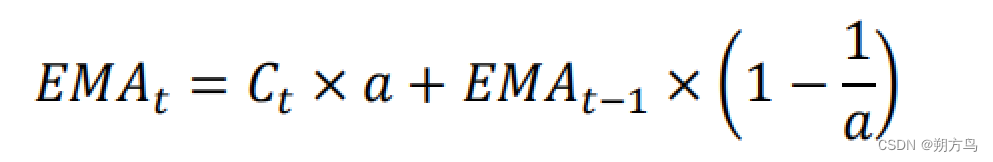
(三)误差分析相关公式
① 方差分析
由于只是分析两组数据的显著性差异,可直接使用方差公式:

② 线性回归分析方程

③ 线性系数求解公式

④ 协方差分析公式
![]()
⑤ 协方差转换公式