MELON的难题

题目描述
MELON有一堆精美的雨花石(数量为n，重量各异)，准备送给S和W。MELON希望送给俩人的雨花石重量一致，请你设计一个程序，帮MELON确认是否能将雨花石平均分配。

---

输入描述
第1行输入为雨花石个数: n，0<n<31。
第2行输入为空格分割的各雨化石重量: m[0] m[1] … m[n- 1]， 0< m[k] < 1001
不需要考虑异常输入的情况。

---

输出描述
如果可以均分，从当前雨花石中最少拿出几块，可以使两堆的重量相等;如果不能均分，则输出-1。

用例

输入	输出	说明
4 1 1 2 2	2	总和为 1+1+2+2=6 那么 可以拿出 重量为1和2的组合 因此至少拿出2块 输出 2
4 1 1 2 2 1	-1	总和为7 为奇数 不可能均分， 输出-1

解析

1. 这个题理解起来简单，看起来也简单，但是写代码时就容易找不清方向了。
2. 首先 输入的数字可以求总和，和为偶数 不可能均分 输出-1 结束
3. 其次 就得开始来组合，至于这个组合怎么去组合，我目前也只想到了数位DP算法，不懂的可以去我的专栏【算法】里面找。使用该算法的话，需要明确的一点是，其实我只需要取出的重量是总和的一半就可以了，不需要计算拿给S多少，W多少。那么例如输入 1 2 3 4
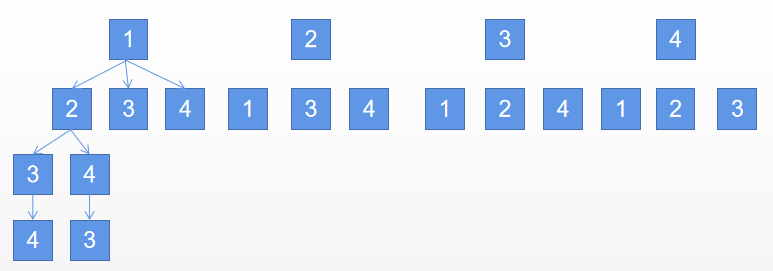
   第一次选择：有四种 1 2 3 4
   第二次选择: 若第一次选1 第二次选择可选 2 3 4 同理 其示意图可以表述为

比如 输入 1 2 3 4 时 如果 第一次取 1 第二次取 2 第三次取 3 三次和为6，超过一半 肯定后面就不往下取了 如果第一次取 2 第二次取3 和为5 刚好，那么2开头的也不往下取了 一次类推，找出所有的可能，并记录最小次数即可。
4. 这个题目中，难点在于数位DP算法，怎么使用且使用时，数组只有一个，因此需要记录前面取到过的索引，组合中值可能重复（重量可能相等），但是索引肯定不重复。

示例代码

import java.util.Scanner;

//MELON的难题
public class T62 {
	static int avg = 0;//
	static int[] tempNum = null;// 取到的数
	static int minCount = 0;
	static int nums[] = null;
	static int tempIndex[] = null;// 取了哪些索引

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int num = Integer.parseInt(sc.nextLine());
		nums = new int[num];
		int sum = 0;
		for (int i = 0; i < num; i++) {
			nums[i] = sc.nextInt();
			sum += nums[i];
		}
		if (sum % 2 != 0) {
			System.out.println(-1);
			System.exit(0);
		}
		avg = sum / 2;
		tempNum = new int[num];
		tempIndex = new int[num];
		for (int i = 0; i < num; i++) {
			tempIndex[i] = -1;
		}
		minCount = num;
		dfs(0, 0);
		System.out.println(minCount);
	}

	public static void dfs(int p, int count) {
		int tempSum = 0;
		for (int i = 0; i < count; i++) {
			tempSum += tempNum[i];
			if (tempSum == avg) {
				if (minCount > count) {
					minCount = count;
				}
				break;
			}
			if (tempSum > avg) {
				// 超了
				return;
			}
		}
		for (int j = 0; j < nums.length; j++) {
			boolean flag = false;
			for (int k = 0; k <= count; k++) {
				if (tempIndex[k] == j) {
					flag = true;
					break;
				}
			}
			if (!flag) {
				tempNum[count] = nums[j];
				tempIndex[count] = j;
				dfs(p + 1, count + 1);
			}
		}
	}
}

代码运行截图