026.【图形结构算法】

news2024/10/6 8:29:55

1. 图的定义

树形结构用于描述节点和节点之间的层次关系，而图形结构用于描述两个顶点之间是否连通的关系。在计算机科学中，图形结构是最灵活的数据结构之一，很多问题都可以使用图来求解。

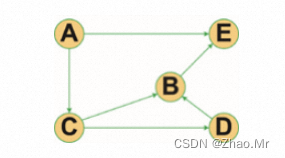
无向图是每条边都没有方向的图，同一个边的两个顶点没有次序关系。例如，(V1,V2)和(V2,V1)表示的是相同的边。
在这里插入图片描述
有向图是每条边都有方向的图，同一个边的两个顶点有次序关系。图中的每一条边都可以使用有序对<V1,V2>来表示。<V1,V2>是指从顶点V1指向顶点V2的一条边，V1表示尾部，而V2表示头部。因此<V1,V2>和<V2,V1>表示不同的两条边。

在这里插入图片描述
图的相关术语：

在这里插入图片描述

2. 图的遍历

图的遍历是指从图中的某个顶点（该顶点也可称为起始点）出发，按照某个特定的方式访问图中的各个顶点，使每个可访问到的顶点都被访问一次。图的遍历方式有两种，一种是深度优先遍历（也叫作深度优先搜索，简称为DFS），还有一种是广度优先遍历（也叫作广度优先搜索，简称为BFS）。

说明：起始点可以任意指定，起始点不同得到的遍历序列也不相同。

注意：在遍历时，每个顶点只能访问一次，不可重复访问。

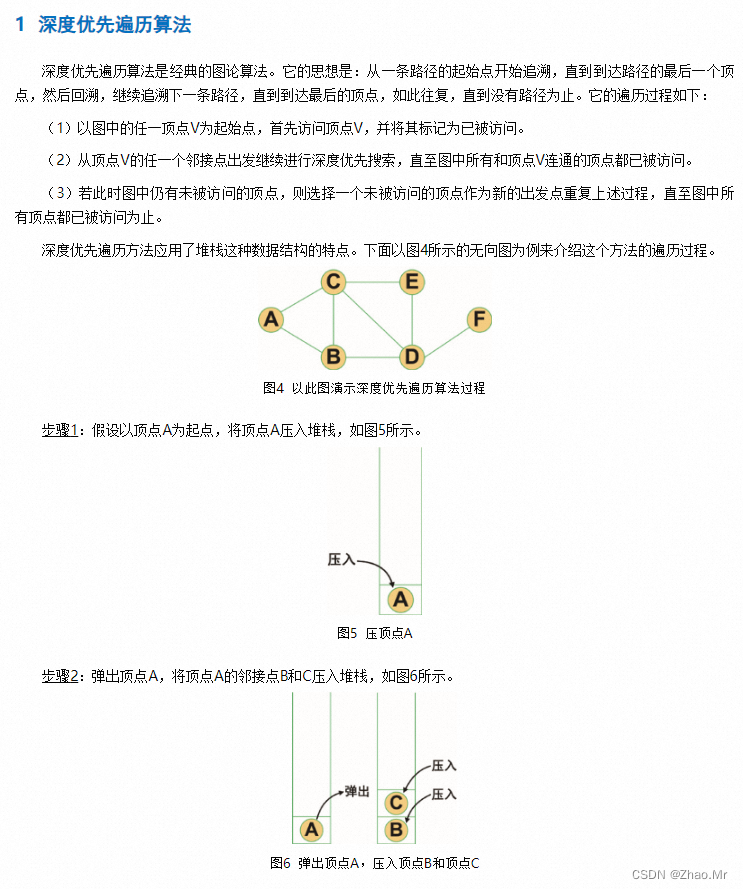
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在该例中应用的深度优先遍历算法，代码如下：

def dfs(graph, start):
    stack = []                                	# 定义堆栈
    stack.append(start)                     	# 将起始顶点压入堆栈
    visited = set()                          	# 定义集合

    while stack:
        vertex = stack.pop()             		# 弹出栈顶元素
        if vertex not in visited:         		# 如果该顶点未被访问过
            visited.add(vertex)       			# 将该顶点放入已访问集合
            print(vertex,end = ' ')     		# 打印深度优先遍历的顶点
        for w in graph[vertex]:         		# 遍历相邻的顶点
            if w not in visited:        		# 如果该顶点未被访问过
                stack.append(w)    				# 把顶点压入堆栈

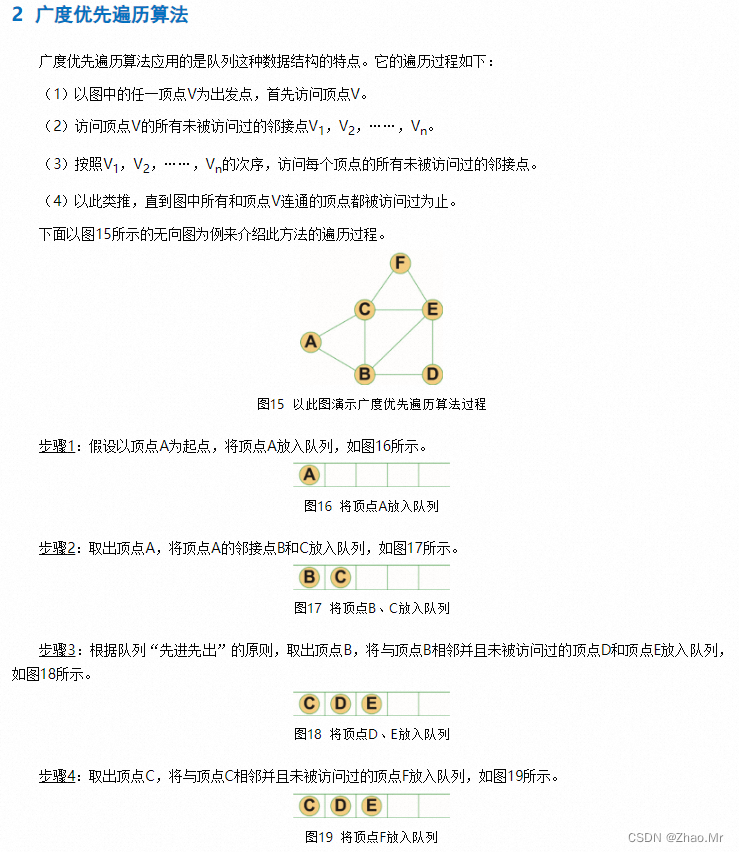
以顶点A为出发点，对该图进行深度优先遍历。
在这里插入图片描述

graph = {                                   		# 定义图的字典
    "A": ["B","C"],
    "B": ["A","D","E"],
    "C": ["A","D","G"],
    "D": ["B","C","F","H"],
    "E": ["B","F"],
    "F": ["D","E","G","H"],
    "G": ["C","F","H"],
    "H": ["D","F","G"],
}

def dfs(graph, start):
    stack = []                              		# 定义堆栈
    stack.append(start)                         	# 将起始顶点压入堆栈
    visited = set()                            		# 定义集合
    while stack:
        vertex = stack.pop()                    	# 弹出栈顶元素
        if vertex not in visited:                   # 如果该顶点未被访问过
            visited.add(vertex)                 	# 将该顶点放入已访问集合
            print(vertex,end = ' ')                 # 打印深度优先遍历的顶点
        for w in graph[vertex]:                  	# 遍历相邻的顶点
            if w not in visited:                  	# 如果该顶点未被访问过
                stack.append(w)             		# 把顶点压入堆栈
                
print("图中各顶点的邻接点：")
for key,value in graph.items():                     # 遍历图的字典
    print("顶点",key,"=>",end=" ")                	# 打印顶点
    for v in value:                            		# 遍历顶点的邻接点
        print(v,end=" ")                      		# 打印顶点的邻接点
    print()

print("深度优先遍历的顶点：")
dfs(graph,"A")                              		# 调用函数并设置起点为A

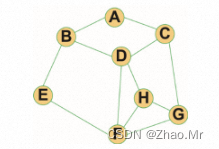
在这里插入图片描述
在这里插入图片描述

在该例中应用的广度优先遍历算法，代码如下：

def bfs(graph, start):
    queue = []                              	# 定义队列
    queue.append(start)                        	# 将起始顶点放入队列
    visited = set()                             # 定义集合
    visited.add(start)                          # 将起始顶点放入已访问集合

    while queue:
        vertex = queue.pop(0)                  	# 取出队列第一个元素
        print(vertex,end = ' ')                 # 打印广度优先遍历的顶点
        for w in graph[vertex]:                 # 遍历相邻的顶点
            if w not in visited:                # 如果该顶点未被访问过
                visited.add(w)              	# 将该顶点放入已访问集合
                queue.append(w)            		# 把顶点放入队列

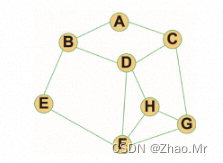
以顶点A为出发点，进行广度优先遍历。

在这里插入图片描述

graph = {                                   		# 定义图的字典
    "A": ["B","C"],
    "B": ["A","D","E"],
    "C": ["A","D","G"],
    "D": ["B","C","F","H"],
    "E": ["B","F"],
    "F": ["D","E","G","H"],
    "G": ["C","F","H"],
    "H": ["D","F","G"],
}

def bfs(graph, start):
    queue = []                              		# 定义队列
    queue.append(start)                        		# 将起始顶点放入队列
    visited = set()                            		# 定义集合
    visited.add(start)                           	# 将起始顶点放入已访问集合

    while queue:
        vertex = queue.pop(0)                  		# 取出队列第一个元素
        print(vertex,end = ' ')                     # 打印广度优先遍历的顶点
        for w in graph[vertex]:                  	# 遍历相邻的顶点
            if w not in visited:                  	# 如果该顶点未被访问过
                visited.add(w)               		# 将该顶点放入已访问集合
                queue.append(w)              		# 把顶点放入队列

print("图中各顶点的邻接点：")
for key,value in graph.items():                     # 遍历图的字典
    print("顶点",key,"=>",end=" ")                	# 打印顶点
    for v in value:                            		# 遍历顶点的邻接点
        print(v,end=" ")                      		# 打印顶点的邻接点
    print()

print("广度优先遍历的顶点：")
bfs(graph,"A")                              		# 调用函数并设置起点为A

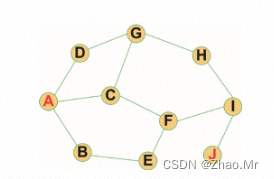
广度优先遍历可以应用在查找最短路径的问题中。假设在A城市到B城市之间有多条线路，每条线路都可能经过一些不同的城镇，应用图的广度优先遍历算法就可以找出A城市到B城市之间的最短路径。找出A城市到J城市之间最短的一条路径。
在这里插入图片描述

# 存储BFS结果
class BFSResult:

    def __init__(self):
        self.visited = []                     	# 已访问顶点
        self.parent = {}                    	# 上一级顶点

# 广度优先搜索
def bfs(graph,start):
    r= BFSResult()
    r.parent = {start:None}                   	# 起始顶点的上一级顶点为None
    r.visited.append(start)                     # 起始顶点加入已访问顶点列表
    fronter = [start]
    while fronter:
        next = []
        for u in fronter:                    	# 遍历上一级顶点
            for v in graph[u]:               	# 遍历当前顶点的相邻顶点
                if v not in r.visited:          # 如果该顶点未被访问
                    r.visited.append(v)      	# 将顶点加入已访问顶点列表
                    r.parent[v] = u        		# 定义当前顶点的上一级顶点
                    next.append(v)
        fronter = next
    return r

# 返回最短路径
def find_shortest_path(bfs_result,end):
    start_vertex = bfs_result.visited[0]        # 起始顶点
    vertex_list = [end]                     	# 最短路径顶点列表
    if end != start_vertex:                 	# 如果设置的终点不是起始顶点
        parent_vertex = bfs_result.parent[end] 	# 获取终点的上一级顶点
        vertex_list.insert(0,parent_vertex)     # 将上一级顶点加入最短路径顶点列表
        while parent_vertex != start_vertex and parent_vertex != None:
            parent_vertex = bfs_result.parent[parent_vertex]
            vertex_list.insert(0,parent_vertex)
    return vertex_list                     		# 返回最短路径顶点列表

if __name__ == '__main__':

    graph = {                             		# 定义图的字典
        'A':['B','C','D'],
        'B':['A','E'],
        'C':['A','F','G'],
        'D':['A','G'],
        'E':['B','F'],
        'F':['C','E','I'],
        'G':['C','D','H'],
        'H':['G','I'],
        'I':['F','H','J'],
        'J':['I']
    }

    bfs_result = bfs(graph,'A')
    print('A城市到J城市的最短路径：')
    result = find_shortest_path(bfs_result, 'J')
    print(' -> '.join(result))

3. 最小生成树

一个图的生成树是以最少的边连通图中的所有顶点，且不产生回路的连通子图。如果一个图有n个顶点，那么生成树会含有图中全部顶点，但只有n-1条边。如果为图的每条边设置一个权重，这种图就叫加权图

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
有四个地区A、B、C、D需要建设水资源工程。假设四个地区自建水库的费用分别是6、5、12、3，各地区之间建立引水管道的费用可以在图中使用权重表示。试着给出一个最优化的水资源配置方案，在保证每个地区都能用上水的前提下，使得整个引水工程需要的费用最低。

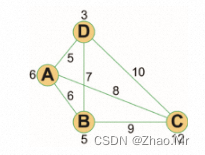
在这里插入图片描述

def prim(graph):
    vertex_list = ["A","B","C","D"]                 	# 顶点列表
    cost = [6, 5, 12, 3]                           		# 费用列表
    visited = [0, 0, 0, 0]                        		# 顶点是否已访问的列表，0表示未访问
    n = len(vertex_list)                         		# 图的顶点个数
    for i in range(0,n):
        k = 0
        min = float("inf")                     			# 最小值初始化
        for j in range(0,n):
            if(not visited[j] and cost[j]<min):
                min = cost[j]               			# 获取费用列表最小值
                k = j                       			# 获取费用列表最小值的索引
        visited[k] = 1                        			# 标记为已访问
        for j in range(0,n):
            if(not visited[j] and graph[k][j]<cost[j]):
                cost[j] = graph[k][j]            		# 更新费用列表
    return cost

def main():
    graph = [[0, 6, 8, 5],                        		# 图的权重列表
             [6, 0, 9, 7],
             [8, 9, 0, 10],
             [5, 7, 10, 0]]

    lowcost = prim(graph)                      			# 调用函数
    total_cost = 0                            			# 总费用初始化
    for n in lowcost:
        total_cost += n                       			# 计算总费用
    print("建立引水工程最小费用列表："+str(lowcost))
    print("四个地区建立引水工程最小费用为"+str(total_cost))

if __name__ == '__main__':
    main()                                  			# 调用函数

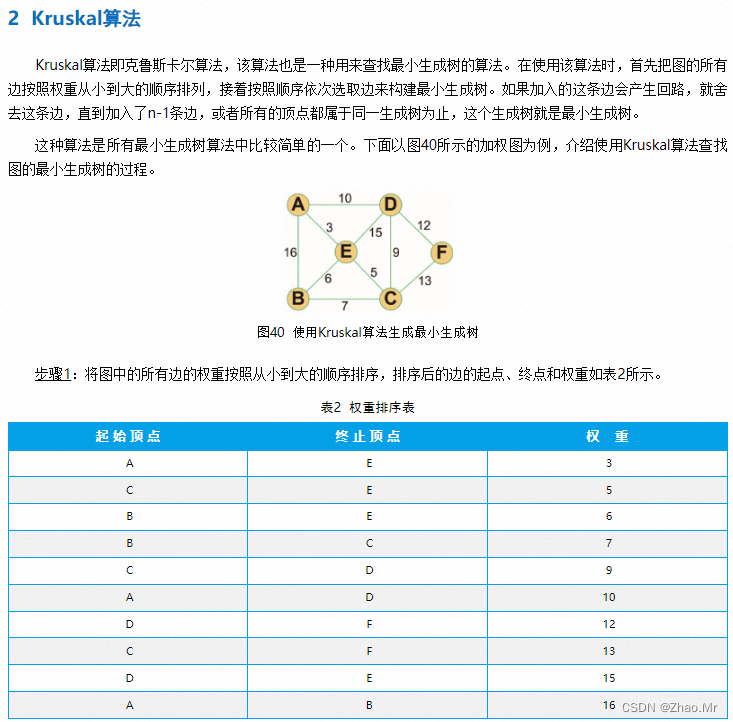
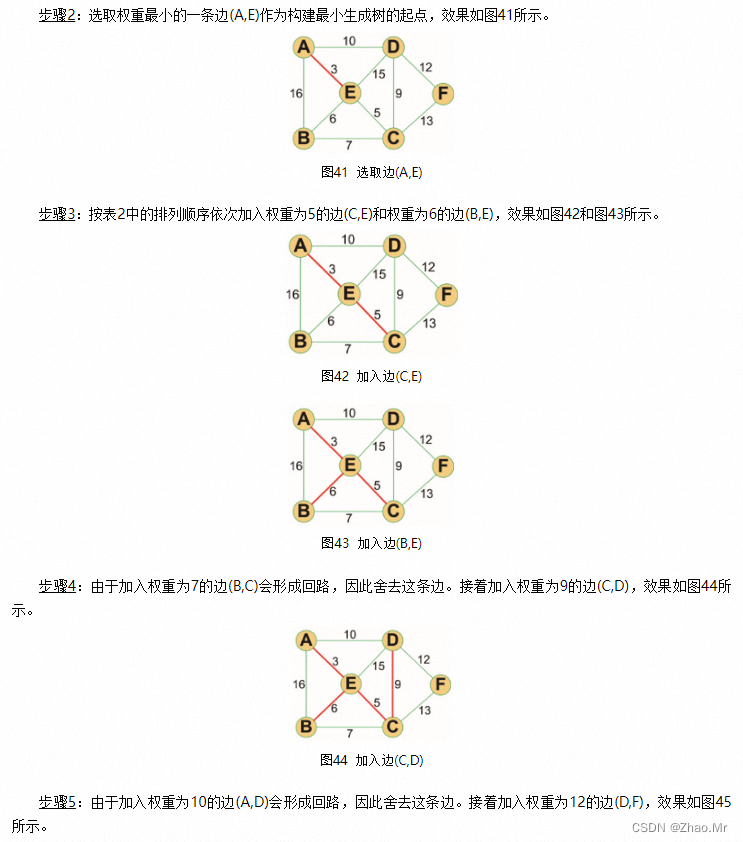
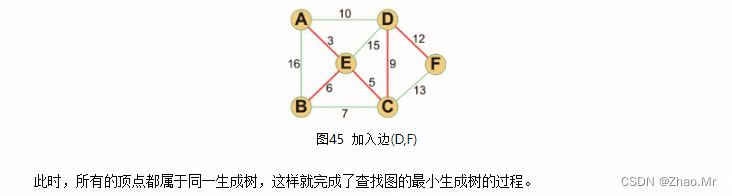
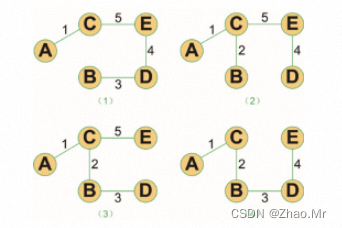
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
应用Kruskal算法获取最小生成树解决各城镇公路互通的问题。一共有七个城镇A、B、C、D、E、F、G，将各城镇之间的公路以及各城镇之间修建公路的成本在图中表示。试着根据给出的数据，求出使每个城镇都有公路连通最低成本的方案。

在这里插入图片描述

def Kruskal(vertex_list, edges):
    all_vertex_list = vertex_list               			# 获取所有顶点列表
    tree_name_list = []                   					# 树名称列表
    for n in all_vertex_list:
        tree_name_list.append(n)          					# 初始化树名称列表
    MST = []                            					# 最小生成树列表
    edges = sorted(edges, key=lambda element: element[2])   # 对所有边按权重升序排列
    while len(MST) != len(vertex_list) - 1:       			# 最小生成树中的边为n-1时退出循环
        element = edges.pop(0)            					# 获取权重最小的边
        vertex_start = element[0]           				# 边的起始顶点
        vertex_end = element[1]           					# 边的终止顶点
        # 起始顶点所在树的名称
        name1 = tree_name_list[all_vertex_list.index(vertex_start)]
        # 终止顶点所在树的名称
        name2 = tree_name_list[all_vertex_list.index(vertex_end)]
        # 如果两个顶点不在同一树中，即加入边后不会形成回路
        if name1 != name2:
            MST.append(element)          					# 把边加入最小生成树列表
            # 将所有树名称name2改为name1
            for n in range(0,len(tree_name_list)):
                if tree_name_list[n] == name2:
                    tree_name_list[n] = name1
    return MST                         						# 返回最小生成树列表

def main():
    vertex_list = ["A","B","C","D","E","F","G"] 			# 图的所有顶点列表
    # 图的所有边组成的列表
    edges = [("A", "B", 10), ("A", "F", 3),
             ("A", "G", 6), ("B", "C", 7),
             ("B", "G", 8), ("C", "D", 9),
             ("C", "G", 5), ("D", "E", 15),
             ("D", "G", 10), ("E", "F", 12),
             ("E", "G", 13), ("F", "G", 9)]

    tree_list = Kruskal(vertex_list, edges)     			# 调用函数
    print("实现各城镇公路互通的方案如下：")
    for n in tree_list:
        print("({:s}—{:s})".format(n[0],n[1]))
    total_price = 0                       					# 最低成本初始化
    for n in tree_list:
        total_price += n[2]                 				# 计算最低成本
    print("\n各城镇公路互通的最低成本："+str(total_price))

if __name__ == '__main__':
    main()                             						# 调用函数

4. 最短路径问题

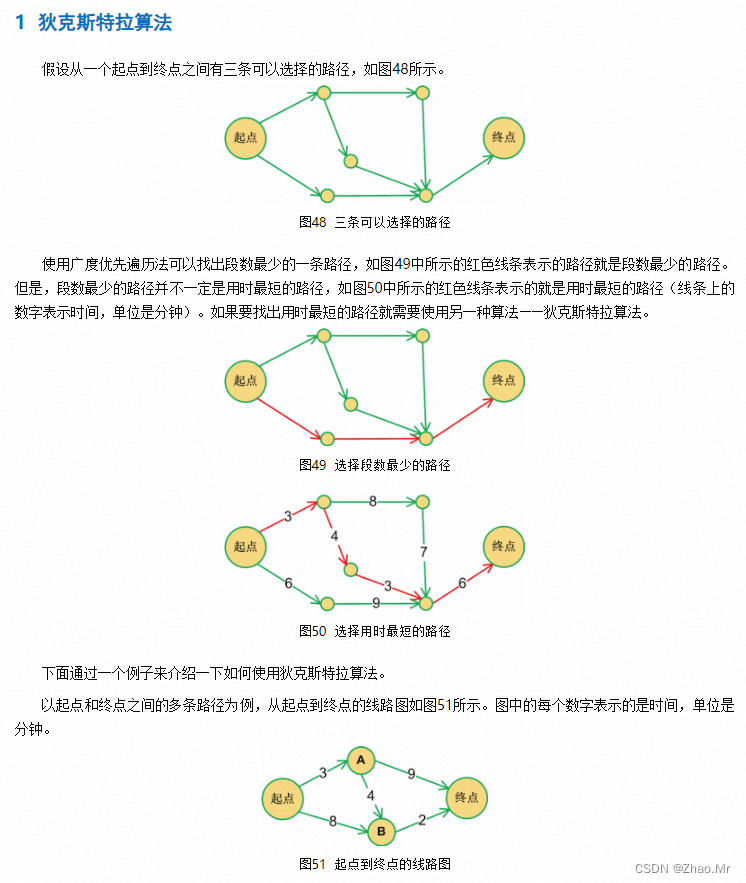
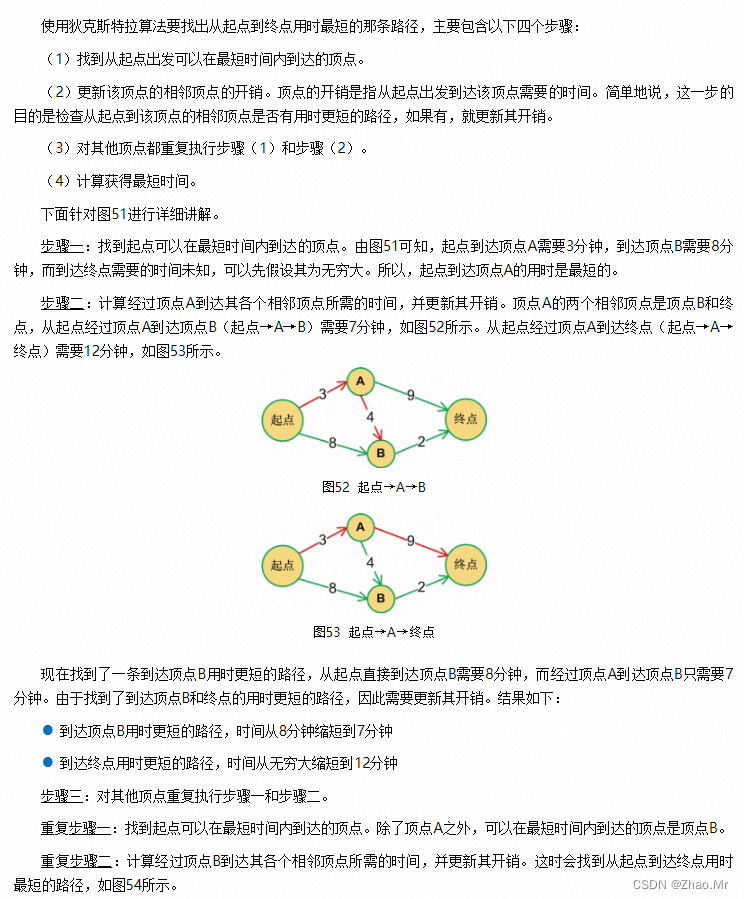
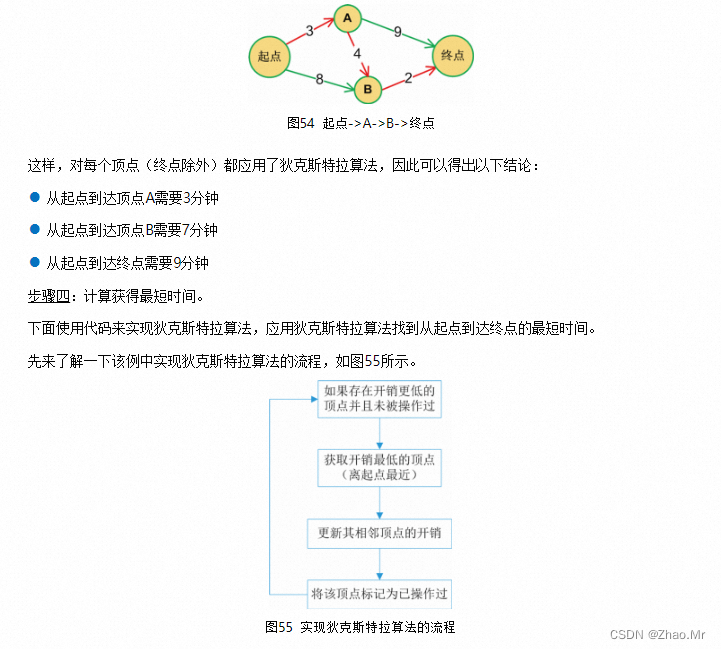
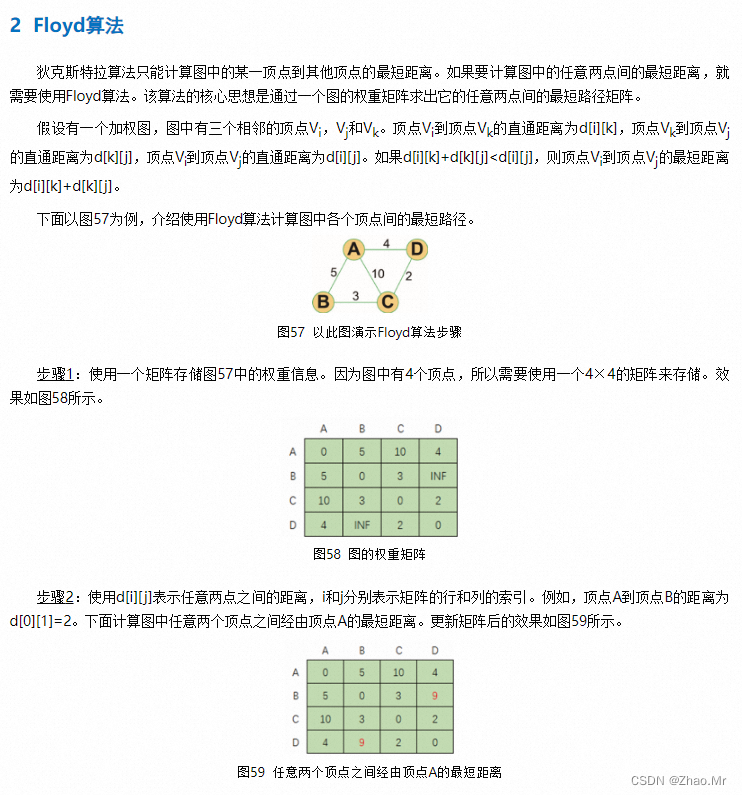
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
通过Floyd算法获取图中所有顶点间的最短路径。
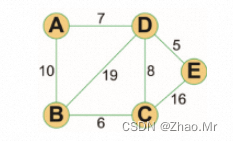
在这里插入图片描述

import math

vertexes = ['A', 'B', 'C', 'D', 'E']                        	# 顶点列表
# 初始化路径矩阵
dis = [[0, 10, math.inf, 7, math.inf],
       [10, 0, 6, 19, math.inf],
       [math.inf, 6, 0, 8, 16],
       [7, 19, 8, 0, 5],
       [math.inf, math.inf, 16, 5, 0]]
vertex_num = len(vertexes)                      				# 顶点个数

for i in range(vertex_num):
    for j in range(vertex_num):
        for k in range(vertex_num):
            # dis[i][j]表示i到j的最短距离
            # dis[i][k]表示i到k的最短距离
            # dis[k][j]表示k到j的最短距离
            # 找到两顶点间的最短距离并更新
            dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j])

print('最短路径矩阵如下：')
print('====================================')
print('      A     B     C     D     E')    					# 打印横向各顶点

for i in range(vertex_num):
    print(vertexes[i], end=' ')                      			# 打印纵向各顶点
    for j in range(vertex_num):
        print('%5d ' %dis[i][j], end='')
    print()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/660947.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

chatgpt赋能python：重新安装Python——让你的编程之路更畅通

chatgpt赋能python：重新安装Python——让你的编程之路更畅通

重新安装Python——让你的编程之路更畅通 Python是一种高级编程语言&#xff0c;广泛应用于软件开发、数据科学、机器学习等领域&#xff0c;因其易学易用、拥有丰富的第三方库和社区支持而备受程序员们的喜爱。但是&#xff0c;有时候你可能会遇到无法解决的Python问题&#…
阅读更多...
Linux 4.10当中将带来深远影响的三项小改变

Linux 4.10当中将带来深远影响的三项小改变

Linux的演进永不停歇。Linus Torvalds一直在努力工作&#xff0c;希望能够在新的内核版本当中(4.11)融入更多变化。不过在目前的Linux 4.10中&#xff0c;我们同样发现了三组能够有效提升性能并实现多种前所未有功能集的变更。 下面&#xff0c;我们将共同了解这些可能对您、您…
阅读更多...
0006-TIPS-2020-hxp-kernel-rop : bypass-KASLR-with-offset_leak

0006-TIPS-2020-hxp-kernel-rop : bypass-KASLR-with-offset_leak

内核默认加载地址&#xff08;不开启KASLR&#xff09; kernel text mapping 在内核linux-5.9/Documentation/x86/x86_64/mm.rst文档中记录了 x86_64虚拟地址空间布局 其中0xffffffff80000000~0xffffffff9fffffff用于存放内核代码段、全局变量、BSS等 ffffffff80000000 | -…
阅读更多...
华为OD机试真题 JavaScript 实现【字符串序列判定】【2022Q4 100分】，附详细解题思路

华为OD机试真题 JavaScript 实现【字符串序列判定】【2022Q4 100分】，附详细解题思路

一、题目描述 输入两个字符串a和b&#xff0c;都只包含英文小写字母。a长度<100&#xff0c;b长度<500,000。 判定a是否是b的有效子串。 判定规则&#xff1a; a中的每个字符在b中都能找到&#xff08;可以不连续&#xff09;&#xff0c;且a在b中字符的前后顺序与a中…
阅读更多...
【SQL应知应会】分析函数的点点滴滴（一）

【SQL应知应会】分析函数的点点滴滴（一）

欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享&#xff0c;与更多的人进行学习交流 本文收录于SQL应知应会专栏,本专栏主要用于记录对于数据库的一些学习&#xff0c;有基础也有进阶&#xff0c;有MySQL也有Oracle 分析函数的点点滴滴 1.什么是分析函数&#xff1a;…
阅读更多...
万字详解常用设计模式

万字详解常用设计模式

本文是博主在工作中对常用设计模式的使用经验总结归纳而来分享给大家。 设计模式一共有23种&#xff0c;本文讲解涉及如下&#xff1a; 责任链模式 模板方法模式 发布订阅模式 策略模式 三大分类 业界一般将设计模式分为三大类&#xff1a; 创建型模式&#xff1a;对类的实…
阅读更多...
chatgpt赋能python：Python怎样调字体大小以及优化网站SEO

chatgpt赋能python：Python怎样调字体大小以及优化网站SEO

Python怎样调字体大小以及优化网站SEO 在现代网络时代&#xff0c;网站的排名和SEO越来越受到关注。有一些关键词和技巧可以用来在搜索引擎排名中获得好的位置。其中一个技术是调整字体大小。在本文中&#xff0c;我们将深入探讨如何使用Python调整字体大小&#xff0c;并进一…
阅读更多...
chatgpt赋能python：Python如何随机产生多个随机数？

chatgpt赋能python：Python如何随机产生多个随机数？

Python如何随机产生多个随机数&#xff1f; Python是一种高级编程语言&#xff0c;它的随机数生成器是其强大的功能之一。在本文中&#xff0c;我们将学习如何使用Python随机数生成器生成多个随机数。 基本概念&#xff1a;随机数生成器 随机数生成器是一种算法或物理设备&a…
阅读更多...
【Python】APScheduler定时调度库

【Python】APScheduler定时调度库

文章目录 APScheduler是什么功能特点四大组件触发器[triggers]date 一次性触发器interval 间隔触发器cron 周期触发器 任务存储器[JobStore]MemoryJobStoreMongoDBJobStoreRedisJobStore示例代码 RethinkDBJobStoreSQLAlchemyJobStoreZooKeeperJobStore 执行器[executors]线程池…
阅读更多...
chatgpt赋能python：Python如何隐藏进程

chatgpt赋能python：Python如何隐藏进程

Python如何隐藏进程 介绍 进程是指运行中的程序在操作系统中的一个实例。在计算机系统中&#xff0c;进程通常都可以被用户或者其他程序所看到。然而&#xff0c;有时候我们需要隐藏进程&#xff0c;比如保护敏感信息或者防止恶意攻击。 Python是一种高级编程语言&#xff0…
阅读更多...
Maven学习笔记（SSM 整合伪分布式案例）

Maven学习笔记（SSM 整合伪分布式案例）

目录 第一节 创建工程&#xff0c;引入依赖 1 创建工程 ①工程清单 ②工程间关系 2、各工程 POM 配置 ①父工程 ②Mybatis 逆向工程 ③环境依赖工程 ④工具类工程 ⑤实体类工程 ⑥组件工程 ⑦Web 工程 第二节 搭建环境&#xff1a;持久化层 1、物理建模 2、Myba…
阅读更多...
leetcode算法 -- 数组

leetcode算法 -- 数组

1 数组 常见的数组算法有双指针&#xff0c;滑动窗口&#xff0c;二分查找和分冶。 2 双指针 核心的思路&#xff1a;使用两个指针&#xff0c;一个从头开始索引&#xff0c;一个从尾开始索引。 2.1 两数之和ii 167 给你一个下标从 1 开始的整数数组 numbers &#xff0c;该…
阅读更多...
chatgpt赋能python：Python怎么随机生成一个数

chatgpt赋能python：Python怎么随机生成一个数

Python怎么随机生成一个数 在Python编程中&#xff0c;经常有需要随机生成一个整数的需求&#xff0c;比如在游戏中生成随机的道具&#xff0c;或者在数据分析中进行随机采样。 Python中提供了一个内置的random模块&#xff0c;可以方便地实现随机生成一个数。 使用random模…
阅读更多...
【Windows】虚拟串口工具VSPD6.9安装

【Windows】虚拟串口工具VSPD6.9安装

【Windows】虚拟串口工具VSPD6.9安装 1、背景2、安装3、补丁4、验证5、下载 1、背景 参考【Windows】虚拟串口工具VSPD7.2安装。 本博客安装的版本是VSPD6.9&#xff0c;并在文末留下下载链接&#xff0c;以供学习研究。 虚拟串口工具一般用来做上位机软件的串口通信调试&…
阅读更多...
Java性能权威指南-总结14

Java性能权威指南-总结14

Java性能权威指南-总结14 堆内存最佳实践对象生命周期管理对象重用 堆内存最佳实践 对象生命周期管理 在很大程度上&#xff0c;Java会尽量减轻开发者投入到对象生命周期管理上的精力&#xff1a;开发者在需要的时候创建对象&#xff0c;当不再需要这些对象时&#xff0c;它们…
阅读更多...
C++11新特性之右值引用

C++11新特性之右值引用

目录 前文 一&#xff0c;什么是右值引用&#xff1f; 二&#xff0c;左值引用和右值引用比较 三&#xff0c;右值引用的应用场景以及作用 四&#xff0c; 右值引用左值的场景分析 五&#xff0c;完美转发 总结 前文 在C98标准后&#xff0c;C11标准的更新为C注入了新活力&…
阅读更多...
chatgpt赋能python：Python如何生成100个随机整数

chatgpt赋能python：Python如何生成100个随机整数

Python如何生成100个随机整数 在Python中&#xff0c;我们可以使用random库来生成随机整数。在本文中&#xff0c;我们将介绍如何使用Python生成100个随机整数。 什么是随机整数 随机整数是指在一定范围内&#xff0c;产生的整数是随机的且不重复的。这在数据分析、机器学习…
阅读更多...
2. CSS的元素显示模式

2. CSS的元素显示模式

了解元素的显示模式可以更好的让我们布局页面. 1.什么是元素的显示模式 2.元素显示模式的分类 3.元素显示模式的转换 2.1什么是元素显示模式 作用:网页的标签非常多&#xff0c;在不同地方会用到不同类型的标签&#xff0c;了解他们的特点可以更好的布局我们的网页。 元素显示…
阅读更多...
chatgpt赋能python：如何在Python中创建模块：完整指南

chatgpt赋能python：如何在Python中创建模块：完整指南

如何在Python中创建模块&#xff1a;完整指南 如果你是一位Python开发者&#xff0c;你肯定需要用到模块。模块使得代码更容易组织和管理&#xff0c;并且可以复用许多代码片段&#xff0c; 提高代码的可重用性。在Python中&#xff0c;模块是一组相关函数&#xff0c;方法和变…
阅读更多...
[论文笔记]End-to-end Sequence Labeling via Bi-directional LSTM-CNNs-CRF

[论文笔记]End-to-end Sequence Labeling via Bi-directional LSTM-CNNs-CRF

引言 本文是论文End-to-end Sequence Labeling via Bi-directional LSTM-CNNs-CRF的阅读笔记。 本论文提出了一个受益于单词级(word)和字符级(character)表示的网络架构，通过组合双向LSTM，CNN和CRF。 简介 首先通过CNN编码一个单词的字符级信息到相应的字符表征。然后组合…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023