换根DP板子题 

D-生活在树上_牛客小白月赛46 (nowcoder.com)

题意：

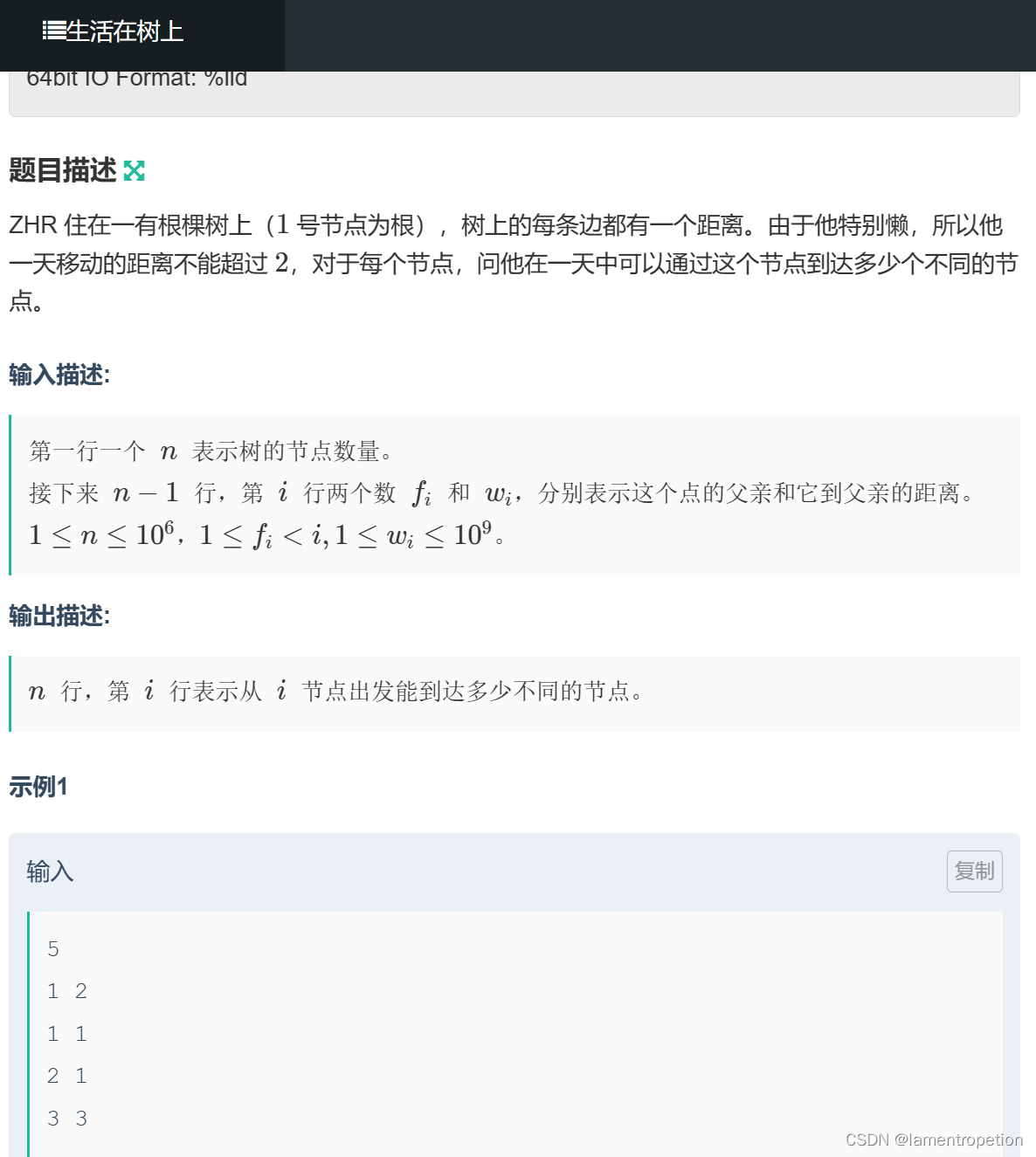
思路：

看数据范围是1e6且是统计问题，求的是对于每一个点的统计问题，那就逃不出是换根DP了

首先dfs1一次把树形DP求出来，然后再考虑换根

设dp[u][j]为以u为根的子树中，离根u的距离是j的结点个数

这个很容易转移，但是注意要对边权分类讨论

然后考虑换根，换根的时候注意是从上到下更新dp数组

是根据u结点的dp值和v的dp值更新儿子结点的dp2值，即dp2[v]=...dp[u]+....的形式

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

using i64 = long long;

const int mxn=1e6+10;
const int mxe=1e6+10;
const int mod=1e9+7;

struct ty{
    int to,next,w;
}edge[mxe<<2];

int N,Fa,d,tot=0;
int head[mxn],dp[mxn][3];

void add(int u,int v,int w){
    edge[tot].w=w;
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void G_init(){
    tot=0;
    for(int i=0;i<=N;i++){
        head[i]=-1;
    }
}
void dfs1(int u,int fa){
    dp[u][0]=1;
    dp[u][1]=dp[u][2]=0;
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        dfs1(edge[i].to,u);
        if(edge[i].w==1){
            dp[u][1]+=dp[edge[i].to][0];
            dp[u][2]+=dp[edge[i].to][1];
        }else if(edge[i].w==2){
            dp[u][1]+=0;
            dp[u][2]+=dp[edge[i].to][0];
        }
    }
}
void dfs2(int u,int fa){
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        if(edge[i].w==1){
            dp[edge[i].to][1]+=dp[u][0];
            dp[edge[i].to][2]+=dp[u][1]-1;
        }else if(edge[i].w==2){
            dp[edge[i].to][2]+=dp[u][0];
        }
        dfs2(edge[i].to,u);
    }
}
void solve(){
    cin>>N;
    G_init();
    for(int i=2;i<=N;i++){
        cin>>Fa>>d;
        add(i,Fa,d);
        add(Fa,i,d);
    }
    dfs1(1,-1);
    dfs2(1,-1);
    for(int i=1;i<=N;i++) cout<<dp[i][0]+dp[i][1]+dp[i][2]<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}

但是注意dfs2不能写成如下形式：

void dfs2(int u,int fa){
    dp2[u][0]=1;
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        if(edge[i].w==1){
            dp2[edge[i].to][1]=dp[edge[i].to][1]+dp[u][0];
            dp2[edge[i].to][2]=dp[edge[i].to][2]+dp[u][1]-1;
        }else if(edge[i].w==2){
            dp2[edge[i].to][1]=dp[edge[i].to][1];
            dp2[edge[i].to][2]=dp[edge[i].to][2]+dp[u][0];
        }
        dfs2(edge[i].to,u);
    }
}

因为父节点被不断更新，这里加上的应该是被更新过的父节点的dp值！

所以在写换根DP的时候，不能另开一个数组，而是累加