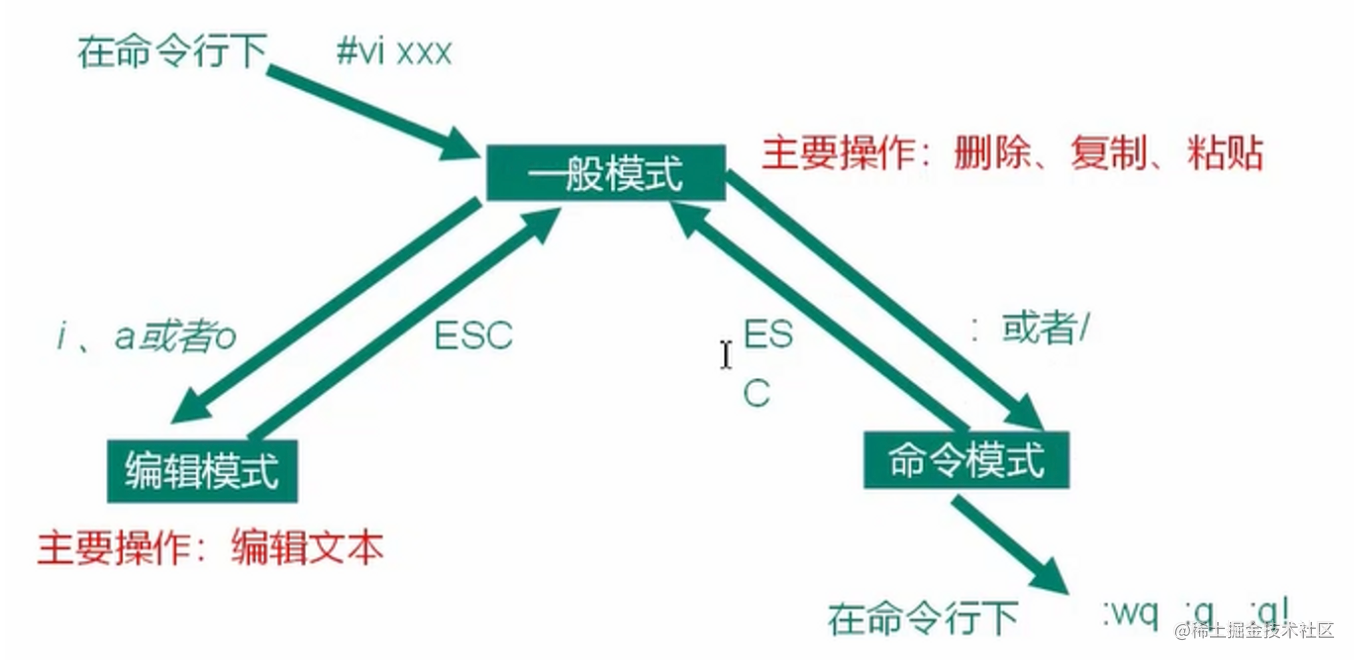
哲学家就餐问题是一个著名的一类同步问题，在并发编程领域，常用来解释线程同步的问题。

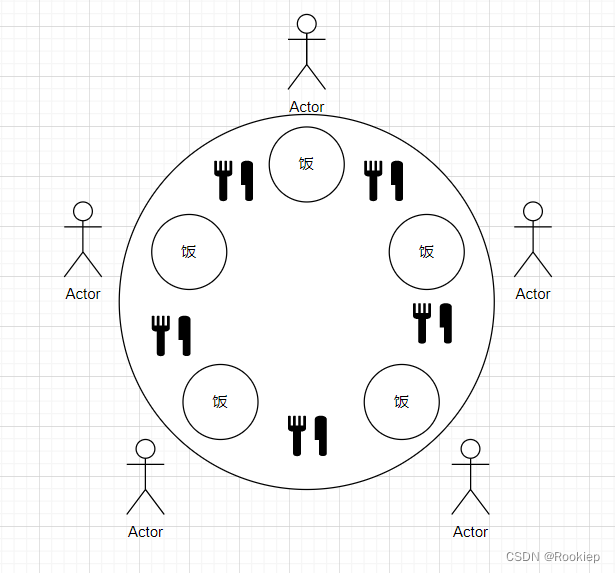
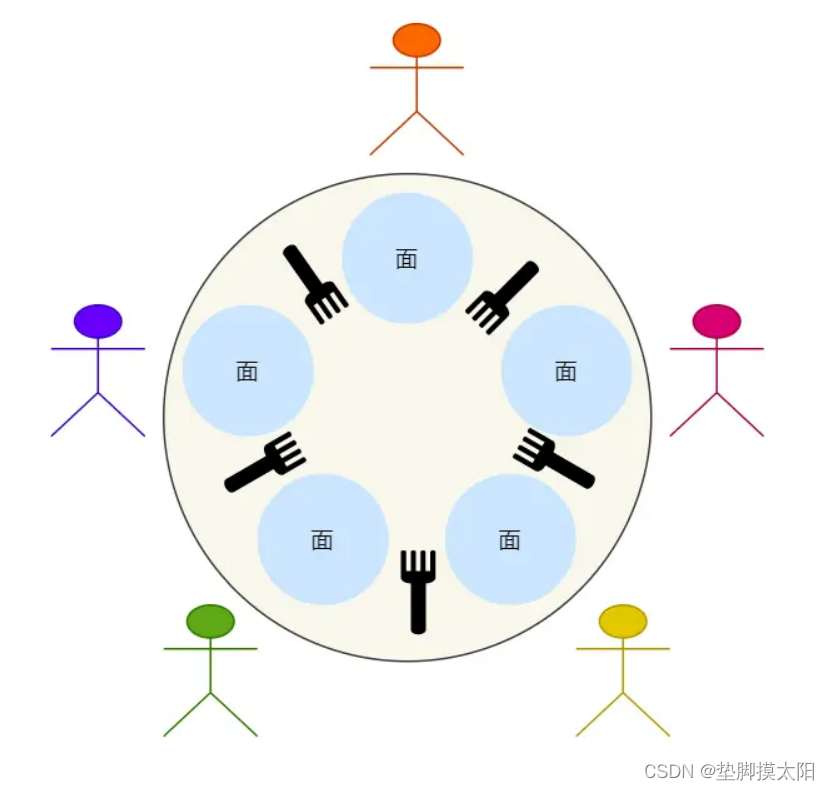
问题描述：五位哲学家围坐在一张圆桌旁，每个哲学家面前有一碗米饭和一只筷子。这五个哲学家都是苦于无法同时持有两只筷子，因为只有当他们拿到两只筷子时才能进食，因此他们时刻面临着这样的问题：如果从左边拿起一只筷子，在等待右边的筷子时，等待时间过长，米饭可能凉掉。如果每个哲学家都等待右边的筷子，那么所有哲学家都将陷入死锁，无法进食。

如何设计一个算法来避免死锁的情况，允许哲学家来进食呢？

图如下：

各种解答方法：

1.资源分配法：保证每个哲学家都有足够的资源，即筷子。避免死锁的方法是保证不会出现所有人想要拿到右边或左边的筷子。

2.时间限制法：约定一个时间限制，哲学家在规定时间内必须把筷子放回去，否则强行让他放筷子。

3.基于信号量：给每一只筷子都建立一个可用性的信号量，当哲学家需要筷子时就会试图“申请”信号量，如果可用则得到信号量掌控筷子，否则该申请被阻塞。

4.设定优先级：为了避免死锁状态，哲学家们可以对筷子数量、进餐时间、可以阻止饥饿状态的优先级等限制加以控制。

5.环状尝试法：为顺时针某一定序列的哲学家设置等待限制，阻止所有哲学家同时拿到右边筷子。比如规定每个哲学家只能先等待左边的筷子，而不能同时等待左右两边的筷子。 

这类问题的解答方法很多，主要在于结合具体情况、场景和问题要求，再采取相应策略，常用的有上述这些方法。

---

我的想法：

1.首先每次只能一个哲学家进食，这样就可以避免死锁问题，但是效率也很低。实现方法是在程序中加入互斥量，这样只要有一个哲学家进入了「临界区」，也就是准备要拿筷子时，其他哲学家都不能动，只有这位哲学家用完叉子了，才能轮到下一个哲学家进餐。

2.5个筷子明显可以满足两个哲学家，我的想法是让奇数序号的哲学家拿筷子，奇数哲学家吃完再让偶数序号的哲学家吃。但是要考虑哲学家的数量，如果总数是奇数，则最后一个奇数哲学家拿不到两个筷子，如上图，奇数哲学家为1，3，5。而5显然拿不到两双筷子！第二个想法明显由于方案一。实现方法是用信号量机制，PV操作就行了。

方案二应该是最优的方案！