代码随想录算法训练营第十四天 |二叉树

news2024/11/24 11:11:57

1.理论基础

二叉树定义

Class TreeNode() {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(){};
    TreeNode(int val) {this.val = val;}
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

二叉树种类
在我们解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树。
满二叉树: 只有度为0和度为2的节点；
完全二叉树：除了最底层可能没填满，其他每层的节点数都是最大值，且最底层的节点都集中在该层的最左边；
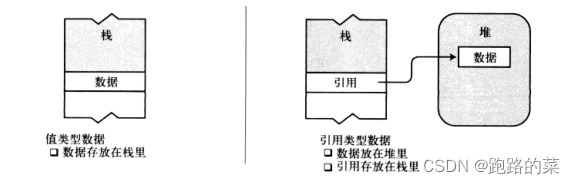
二叉树存储方式
主要为链表方式和数组方式；

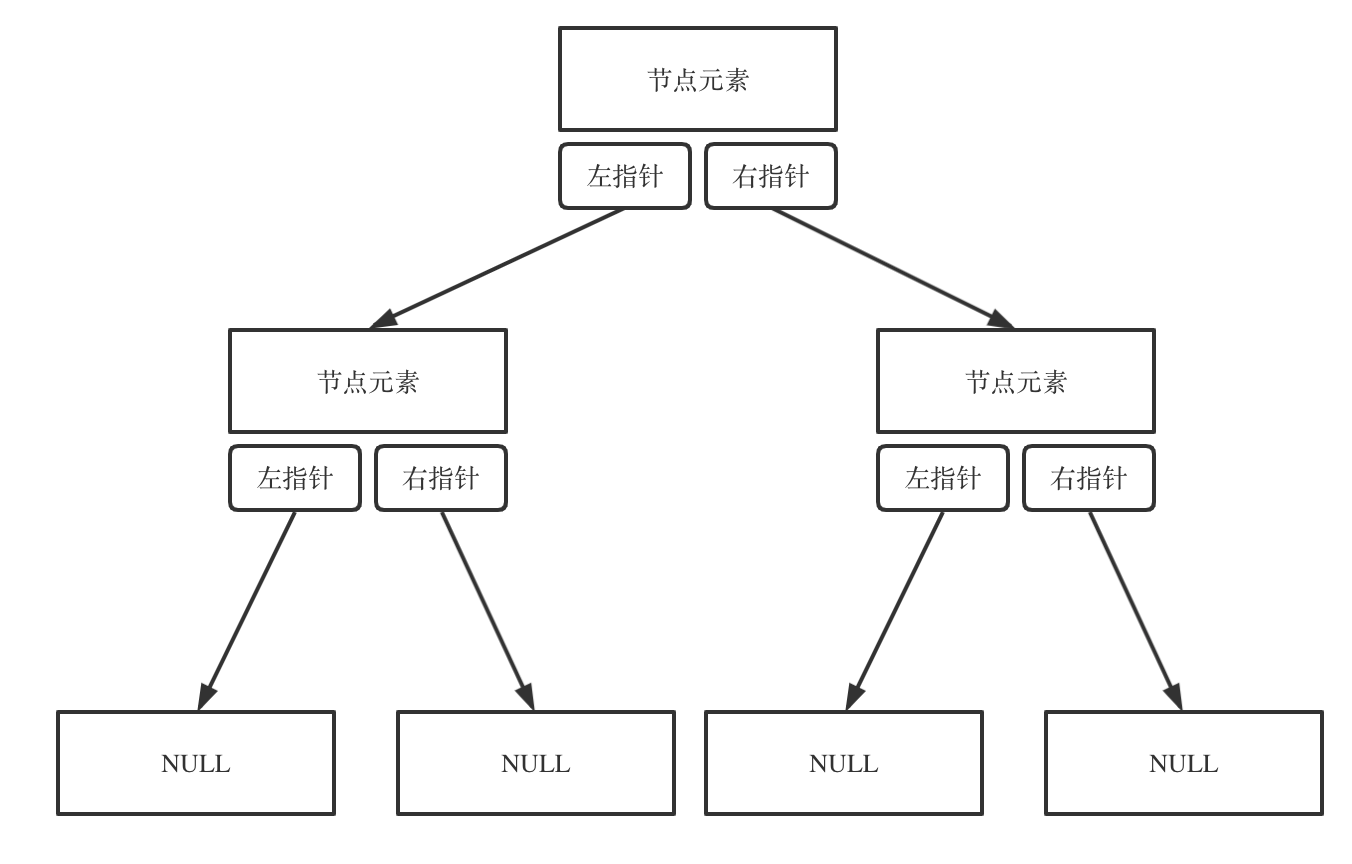
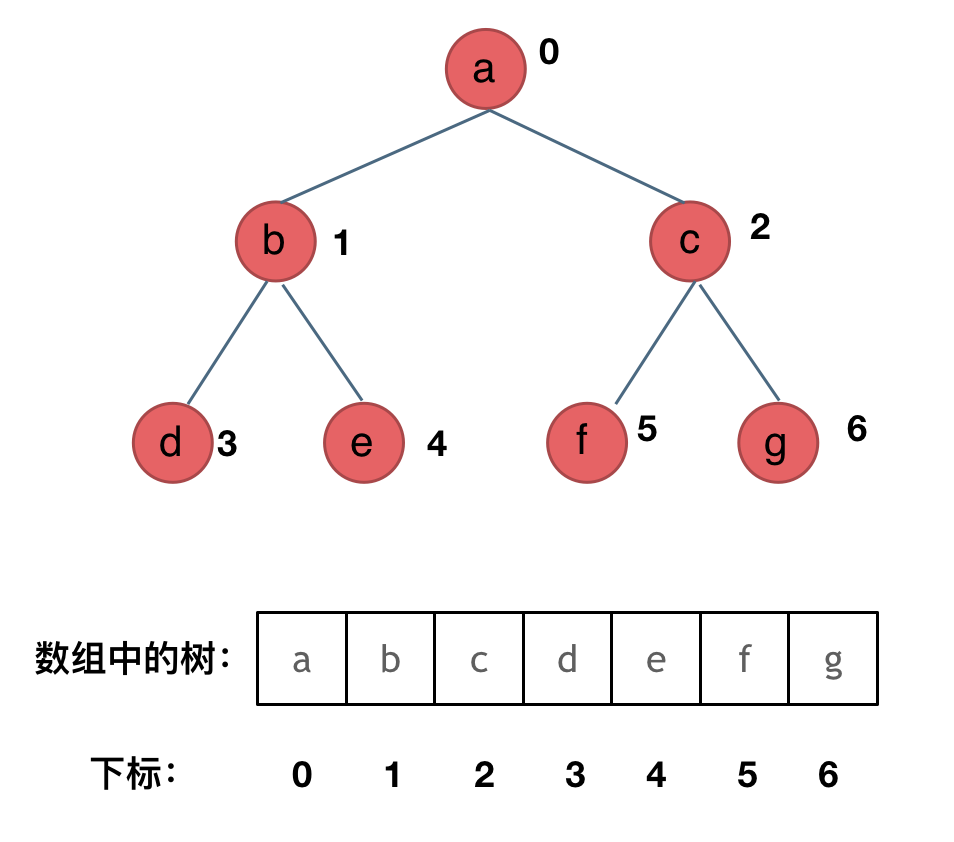
二叉树的遍历方式
深度优先遍历：下面的前中后指的是中间节点的遍历位置

前序遍历（中左右）
递归法：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        // 迭代终止条件
        if (root == null) {
            return;
        }
        // 中左右
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

迭代法：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null){
                stack.push(node.right);
            }
            if (node.left != null){
                stack.push(node.left);
            }
        }
        return result;
    }
}

中序遍历（左中右）
递归法:

// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        // 左中右
        inorder(root.left, list);
        list.add(root.val);             
        inorder(root.right, list);
    }
}

迭代法：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
}

后序遍历（左右中）
递归法：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }

    void postorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        // 左右中
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);             
    }
}

迭代法：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}