[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A2CiIK0R-1687071926271)(data:image/svg+xml;utf8, )]
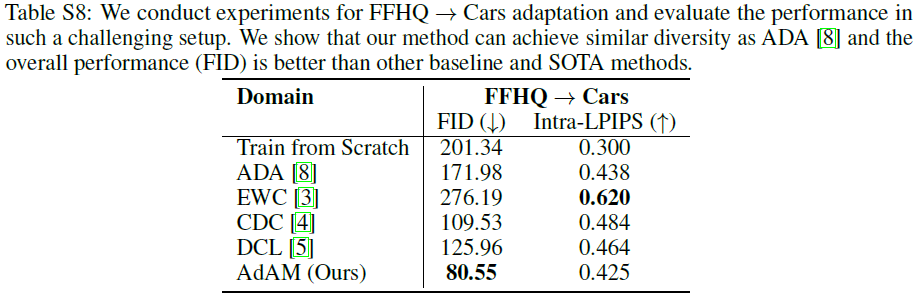
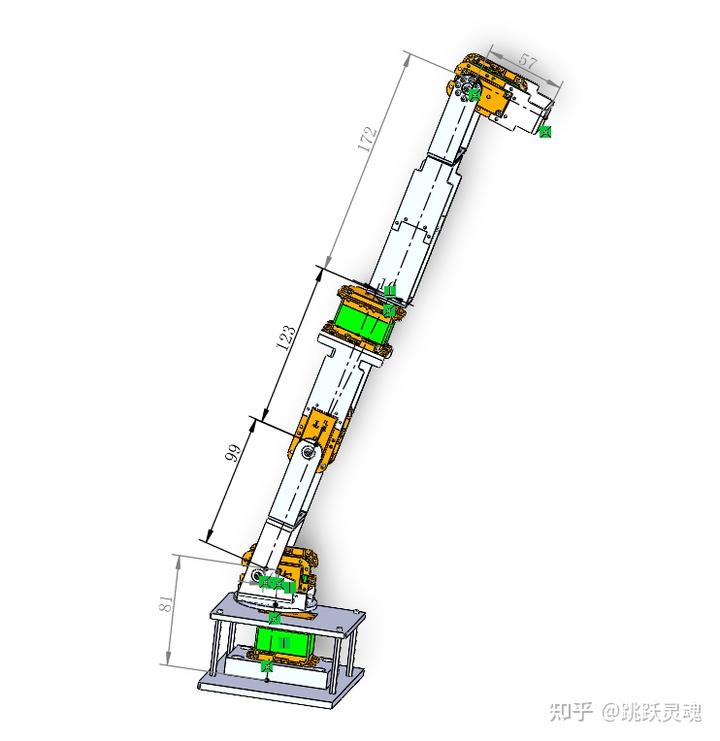
五轴机械臂正逆解仿真
- 标准的D-H参数法
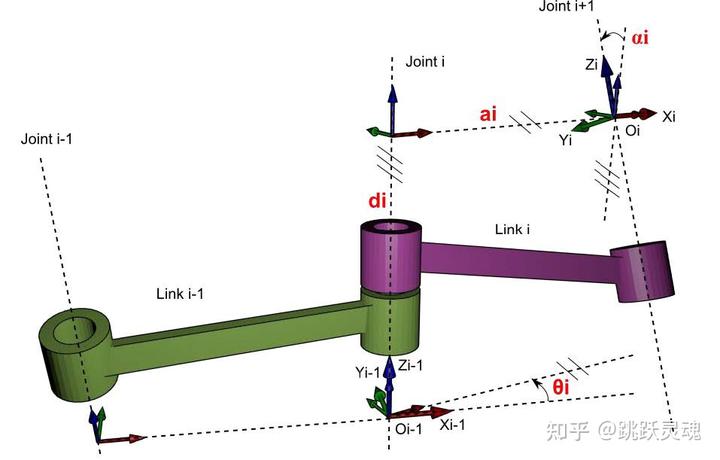
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PbUOp13D-1687071926272)(data:image/svg+xml;utf8, )]
图Ⅰ机器人D-H连杆坐标系
将连杆坐标系的原点建立在连杆的关节连杆末端。
一、建立D-H连杆坐标系的原则
1.Z,轴沿关节轴i+1的轴向。
2.原点O为Zi.,与Zi轴的交点或其公垂线与关节轴Zi的交点。3.Xi轴沿Zi与Zi轴的公垂线方向,由关节轴i指向关节轴i+1。4.Yi轴按照右手定则确定。
二、D-H参数的含义
1.连杆长度ai:定义为从Zi-1移动到Zi的距离,沿Xi轴指向为正。其实质为公垂线的长度。
2.连杆转角αi:定义为从Z i-1旋转到zi的角度,绕Xi轴正向旋转为正。
3.关节偏距di,:定义为从X i-1移动到Xi的距离,沿Z i-1轴指向为正。其实质为两条公垂线之间的距离。
4.关节角0i,:定义为从X i-1旋转到Xi的角度,绕Zi轴正向旋转为正。
三、相邻坐标系之间的齐次变换矩阵

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fB1V6pkb-1687071926273)(data:image/svg+xml;utf8, )]
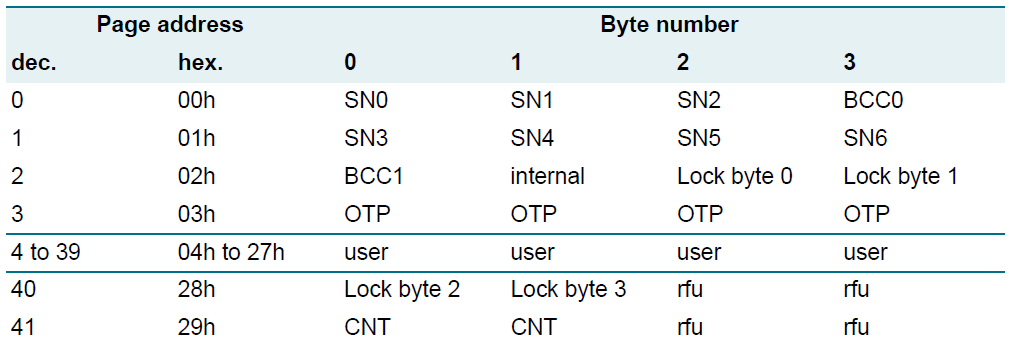
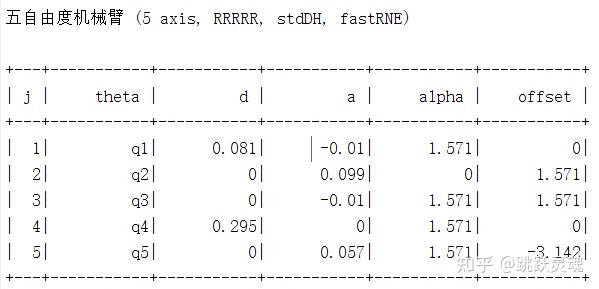
DH参数表如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-84OdsOGL-1687071926274)(data:image/svg+xml;utf8, )]
正运动学分析
根据D-H表规定得到如下变换矩阵为:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WTsqF7L4-1687071926275)(data:image/svg+xml;utf8, )]
正运动学验证分析
正运动学函数
function [ T05 ] = fkine(JD)
%JD为输入的1*5的数组,代表5个关节变量
% trans( theta, d, a, alpha )
if nargin<2; end
T01 =trans( JD(1), 0.081, -0.01, pi/2);
T12 =trans( JD(2)+pi/2, 0, 0.099, 0);
T23 =trans( JD(3), 0, -0.01, pi/2);
T34 =trans( JD(4), 0.172+0.123, 0, pi/2 );
T45 =trans( JD(5)-pi, 0, 0.057, pi/2 );
T05 =T01*T12*T23*T34*T45;
End
正运动学子程序-旋转矩阵
%输入JD,即6个关节变量的值,求解正运动方程
%标准D-H
function [ T ] = trans( theta, d, a, alpha )
T =[
cos(theta), -sin(theta)*cos(alpha), sin(theta)*sin(alpha), a*cos(theta);
sin(theta), cos(theta)*cos(alpha), -cos(theta)*sin(alpha), a*sin(theta);
0, sin(alpha), cos(alpha), d;
0, 0, 0, 1 ];
End
主程序如下:
%正运动学分析
init_ang=[0 45*pi/180 0 -36*pi/180 0];%起点
disp(‘工具箱求解得到旋转矩阵如下:’)
T=robot.fkine(init_ang) %正运动学
disp(‘通过变换矩阵求解旋转矩阵如下:’)
%自定义矩阵
fkine(init_ang) %验证正运动学方程的正确性
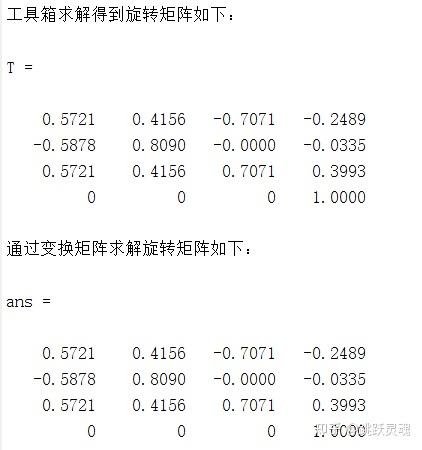
运行结果如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9M7ip5VI-1687071926304)(data:image/svg+xml;utf8, )]
观察可知两个矩阵一样,说明整个正运动学分析正确
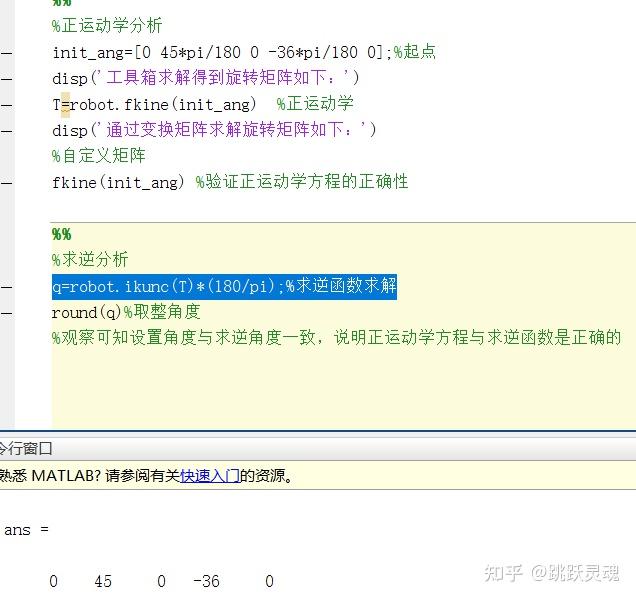
逆运动学分析
根据正运动学分析设置角度,反向求解关节角度,具体程序如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7UYqhoXH-1687071926305)(data:image/svg+xml;utf8, )]
%观察可知设置角度与求逆角度一致,说明正运动学方程与求逆函数是正确的
机器人模型建立
所设计的机器人由多个连杆机构组成,其关节类型包括旋转关节和移动关节两种。利用Matlab中机器人仿真工具箱Robotics Tool中Link和SerialLink两个函数可建立机器人模型[]。其中,函数表达式如下:
式中,theta为关节变量;_d_为偏置距离;alpha为扭转角;_a_为连杆长度;sigma表示关节类型(0为旋转关节,1为移动关节);前四个参数分别对应表1中的

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oH4bfQB9-1687071926305)(data:image/svg+xml;utf8, )]
,

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yFBnbsDd-1687071926306)(data:image/svg+xml;utf8, )]
,

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B1g7yJY4-1687071926306)(data:image/svg+xml;utf8, )]
,

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CNQBTXZ6-1687071926307)(data:image/svg+xml;utf8, )]
。
具体程序编制如下:
L(1) = Link( ‘d’, 0.081, ‘a’ ,-0.01 , ‘alpha’, pi/2 ,‘offset’,0);
L(2) = Link( ‘d’, 0 , ‘a’ , 0.099 , ‘alpha’, 0 ,‘offset’,pi/2);
L(3) = Link( ‘d’, 0 , ‘a’ , -0.01 , ‘alpha’,pi/2,‘offset’,pi/2);
L(4) = Link( ‘d’, 0.172+0.123, ‘a’ , 0 , ‘alpha’, pi/2 ,‘offset’,0);
L(5) = Link( ‘d’,0 , ‘a’ , 0.057 , ‘alpha’,pi/2,‘offset’,-pi);
% L(6) = Link( ‘d’, 0.225 , ‘a’ , 0 , ‘alpha’,0,‘offset’,0);
robot = SerialLink(L,‘name’,‘五自由度机械臂’); %建立连杆机器
robot.display;
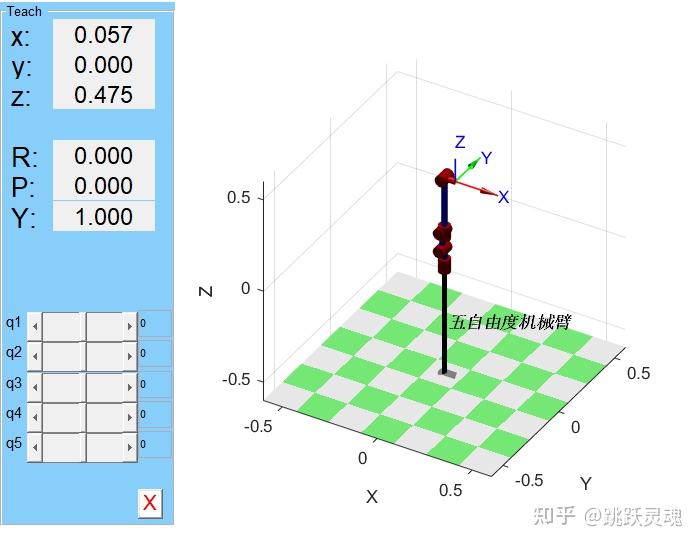
robot.teach; %画出模型并进行调控
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PVpuqOxQ-1687071926308)(data:image/svg+xml;utf8, )]
图 3-3机器臂模型
下载咨询链接
三维模型+word+全仿真代码下载链接