直接选择排序

以升序排序为例

文章目录

直接选择排序
- 算法步骤
- 动图演示
- 实现代码
- 改进算法（双指针）
- - 具体步骤
  - 处理特殊情况：
  - 实现代码
- 时间复杂度

算法步骤

方法一：直接交换数组元素

将第一个元素与其他元素进行比较，若其他元素小于第一个元素，则交换位置，最后第一个元素为最小元素
将剩余元素的第一个元素与其他元素进行比较，若其他元素小于第一个元素，则交换位置
重复上述步骤，直到第（n-1）个元素比较完毕

方法二：利用数组下标间接交换数组元素

将第一个元素的下标标记为min，将第一个元素与其他元素进行比较，若其他元素小于第一个元素，则令该元素的数组下标为min，一轮比较完后，若第一个元素的下标不等于min，则交换第一个元素与下标为min的元素的位置
对剩下的元素重复上述步骤，直到没有元素需要交换位置

动图演示

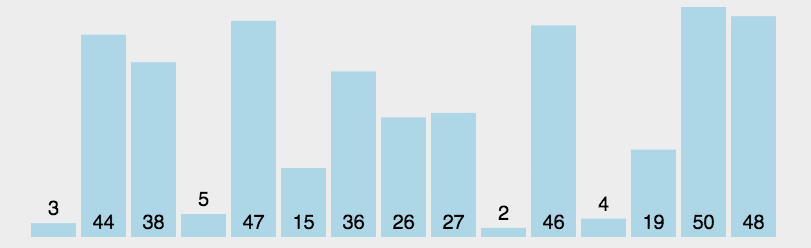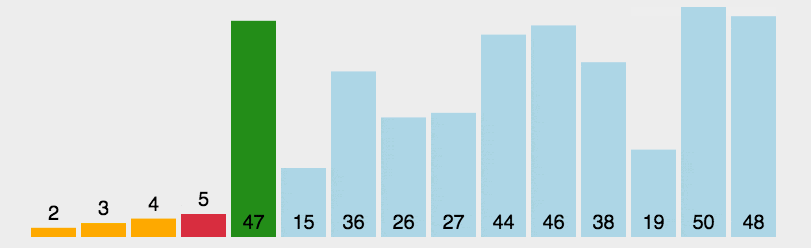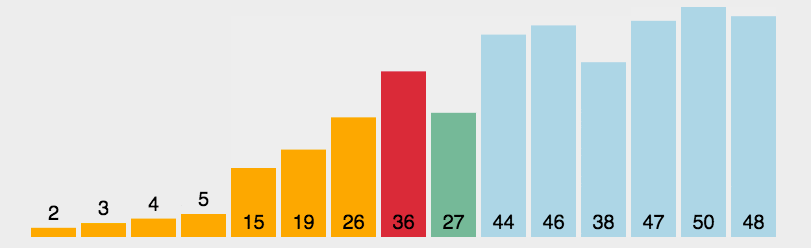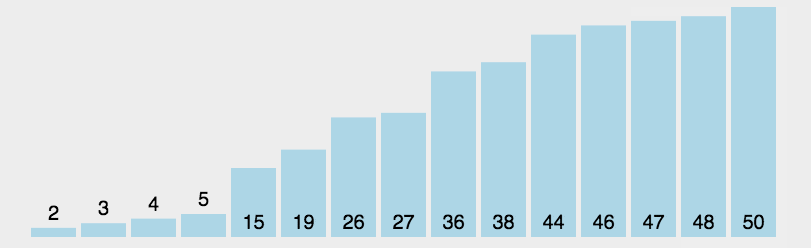
实现代码

#include<stdio.h>
void WayOne(int *p,int num)		//利用直接交换数组元素，从小到大排列数组
{
   int i,j,temp;
   for(i=0;i<num-1;i++)		//需比较（数组元素-1）次
   	for(j=i+1;j<num;j++)
   		if(p[i]>p[j])
   		{
   			temp=p[i];
   			p[i]=p[j];
   			p[j]=temp;
   		}
   for(i=0;i<num;i++)
   	printf("%-5d",p[i]);
}
void WayTwo(int *p,int num)		//利用元素下标间接交换数组元素，从大到小排列数组
{
   int i,j,temp,max;
   for(i=0;i<num-1;i++)
   {
   	max=i;			//设置标记
   	for(j=i+1;j<num;j++)
   		if(p[j]>p[max])
   			max=j;
   	if(max!=i)
   	{
   		temp=p[max];
   		p[max]=p[i];
   		p[i]=temp;
   	}
   }
   for(i=0;i<num;i++)
   	printf("%-5d",p[i]);
}
int main()
{
   int a[]={12,134,46,688,563,145,7357,26,24};
   WayOne(a,sizeof(a)/sizeof(int));
   printf("\n");
   WayTwo(a,sizeof(a)/sizeof(int));
   return 0;
}

改进算法（双指针）

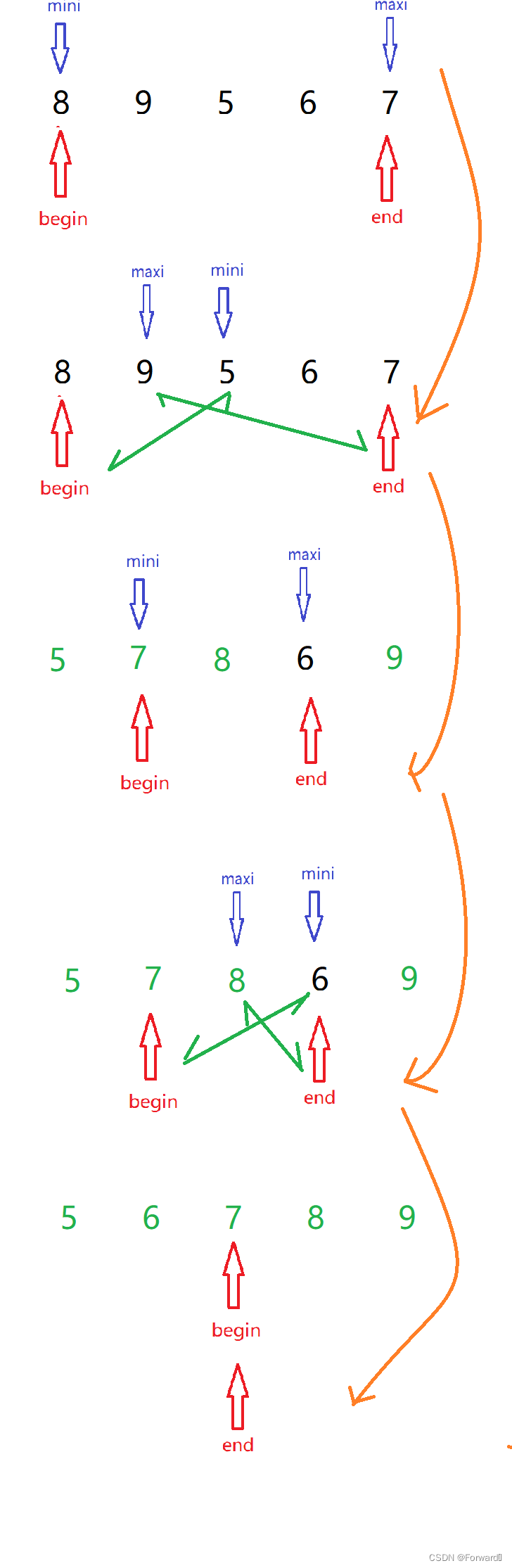
具体步骤

上面的直接选择排序每一次只能选出一个数据，但是，我们可以用双指针的方法进行改进，做到每一次可以选出两个数据
首先，我们令begin指向数组第一个元素，end指向数组最后一个元素
然后，遍历[begin,end]这一块区域，同时保存最大值和最小值元素的下标max_index、min_index
由于进行的是升序排序，begin位置应该放置最小值，end位置应该放置最大值，我们就可以利用下标来交换begin、min_index和end、max_index的数据
缩小区域[begin,end]，重复上述步骤，直到不能满足条件begin < end

实现代码

void SelectSort(int* nums, int numsSize)
{
	int begin = 0;
	int end = numsSize - 1;
    
	while (begin < end)
	{
		int max_index = end;
		int min_index = begin;
		for (int i = begin; i <= end; i++)
		{
            //得到最小值的下标
			if (nums[i] < nums[min_index])
				min_index = i;
            
            //得到最大值的下标
			if (nums[i] > nums[max_index])
				max_index = i;
		}
        
        //将最小值放到前面
		Swap(&nums[begin], &nums[min_index]);
        
        //将最大值放到后面
		Swap(&nums[end], &nums[max_index]);
        
        //缩小区间
		begin++;
		end--;
	}
}

具体过程：

处理特殊情况：

如果遍历完后存在这么一种情况：
我们执行完第一次交换Swap(&nums[begin],&nums[min_index])后：
再执行第二次交换Swap(&nums[end], &nums[max_index]):
我们发现，最小值-1竟然被放到了最后，这显然是不对的，为什么会出现这样的情况呢？
出现这种情况是因为：最大值元素的下标刚好是begin，当我们执行第一次交换Swap(&nums[begin], &nums[min_index])后，begin（max_index）代表的值就是最小值，因此当我们执行第二次交换Swap(&nums[end], &nums[max_index])时，就会将最小值放到最后（即end的位置）

为了避免这种情况，应该在第一次交换后进行一次判断，对max_index的位置进行修正

/*
	如果 begin == max_index
	那么第一次交换Swap(&nums[begin], &nums[min_index])后，min_index的值其实是最大值
	因此，要将max_index的值修正为min_index
*/
if (begin == max_index)
    max_index = min_index;

实现代码

void Swap(int* num1, int* num2)
{
	int temp = *num1;
	*num1 = *num2;
	*num2 = temp;
}

void SelectSort(int* nums, int numsSize)
{
	int begin = 0;
	int end = numsSize - 1;
    
	while (begin < end)
	{
		int max_index = end;
		int min_index = begin;
       for (int i = begin; i <= end; i++)
		{
            //得到最小值的下标
			if (nums[i] < nums[min_index])
				min_index = i;
            
            //得到最大值的下标
			if (nums[i] > nums[max_index])
				max_index = i;
		}
        
        //将最小值放到前面
		Swap(&nums[begin], &nums[min_index]);
        
        //对max_index进行修正
		if (begin == max_index)
			max_index = min_index;
        
        //将最大值放到后面
		Swap(&nums[end], &nums[max_index]);
        
        //缩小区间
		begin++;
		end--;
	}
}