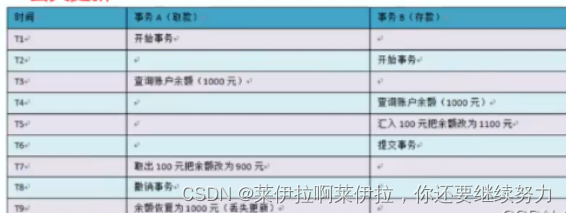
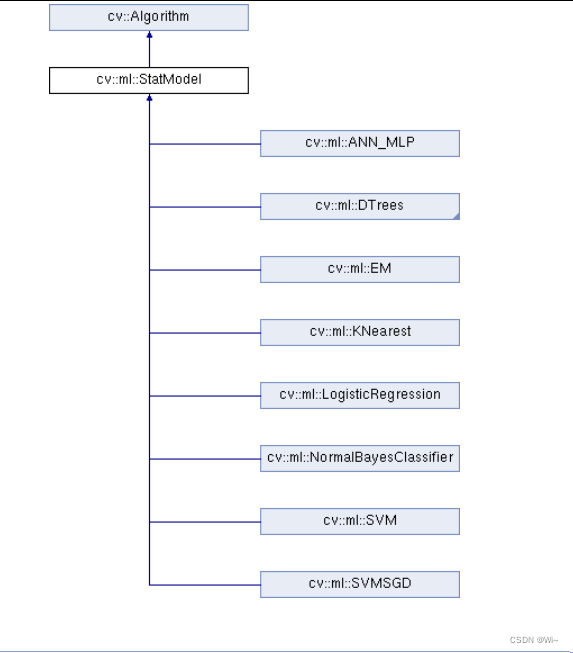
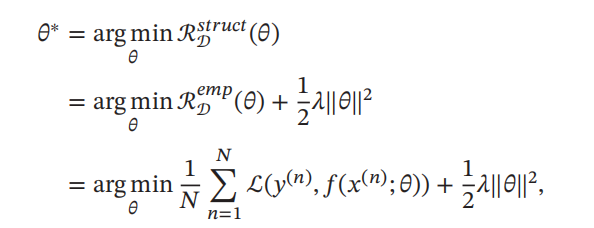训练集是有N个独立同分布的样本组成，即每个样本(x,y)是独立的从相同的分布中抽取的。这个真实的分布未知

输入空间X和输出空间Y构成样本空间，对于样本空间中的样本(x, y)∈X x Y，假定x和y之间可通过一个未知的真实隐射y=g(x)来描述，或者通过真实条件概率分布来描述。

1 期望风险

要评价模型f(x, θ)的好坏，可通过期望风险R(θ)来衡量：

 

回顾一下数学期望的含义，

期望E[X]的含义是随机变量x与概率密度函数f(x)相乘以后的积分

期望E[g(X)]的含义是随机变量的函数g(x)与概率密度函数f(x)相乘以后的积分

现在求R(θ)，即损失函数与真实分布相乘以后的积分（可能是多重积分）

求期望损失R(θ)不仅需要知道损失函数还需要知道真实分布,损失函数可以通过一定的准则计算得到，但是样本空间的真实分布是未知的。所以不能直接求R(θ)。

2 经验风险和经验风险最小化

期望风险R(θ)无法计算，给定一个训练集D = ，我们可以计算经验风险，经验风险就是在训练集上的平均损失：

emp就代表经验损失Empirical Risk

学习准则就是找到一组参数使得经验风险最小化：

这就是经验风险最小化准则。

3 结构风险和结构风险最小化

根据大数定理，训练集D的大小无限大时，经验风险就趋于期望风险，但是通常情况下训练样本时真实数据的一个很小的子集，并且包含噪声。如果一味的使得在训练集上的经验风险最小，有可能使得在未知数据上的错误率很高。这就是出现了过拟合。过拟合的是由于训练数据少，训练数据上有噪声，以及模型能力过强造成的。

为了解决过拟合问题，引入了参数正则化来限制模型的能力。使其不要过度的最小化经验风险。这种准则就是结构风险最小化准则：