就是要我们非递归其实就是模仿递归的写法，类如递归一样遍历一棵树，但是却不是递归的写法，

防止栈溢出。

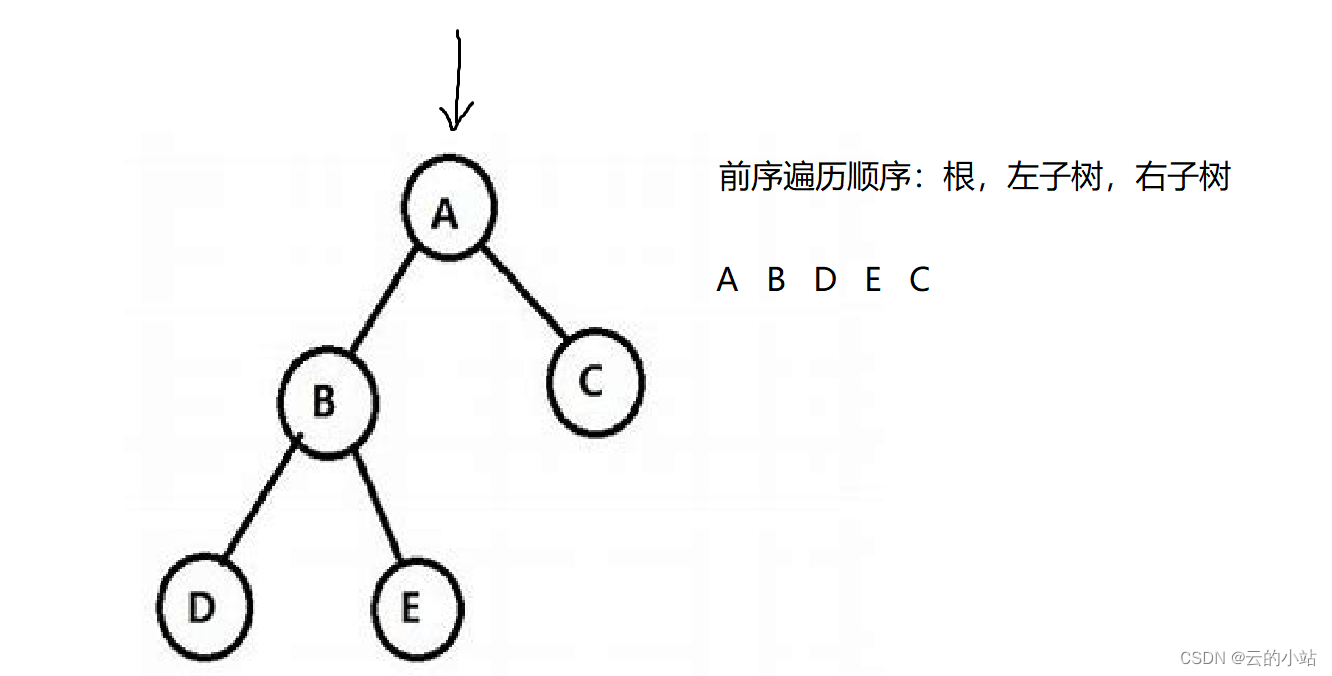
二叉树的前序遍历

先看递归代码：

void _preorderTraversal(TreeNode* root,vector<int>&v)
{
    if (root == NULL)
	{
		return;
	}
	v.push_back(root->val);
	preorderTraversal(root->_left);
	preorderTraversal(root->_right);
}


vector<int> preorderTraversal(TreeNode* root)
{
    vector<int> v;
     _preorderTraversal(root,v);
    return v;
}

        递归遍历访问到nullptr时，可以返回上一层结点，再去访问右子树。这里我们是在上一级栈帧中保存了直系父节点才做到，当该父节点结束以后代表他的左右结点都访问完毕，然后再返回他的上一层结点（B的左右结点访问完毕，返回到A，再去访问C）为什么能再次返回呢？因为每一层栈帧保存了一个父节点。我们的非递归就是要做到这样的情况。类似栈帧的完成方法实现，这就要使用到我们的栈了。

我们规定了遍历顺序都是先遍历左子树再遍历右子树，所以我们的前序遍历就要先访问左子树

 每到一个非空树时就要将根结点保存在栈中.然后继续访问左子树cur=cur->left

 

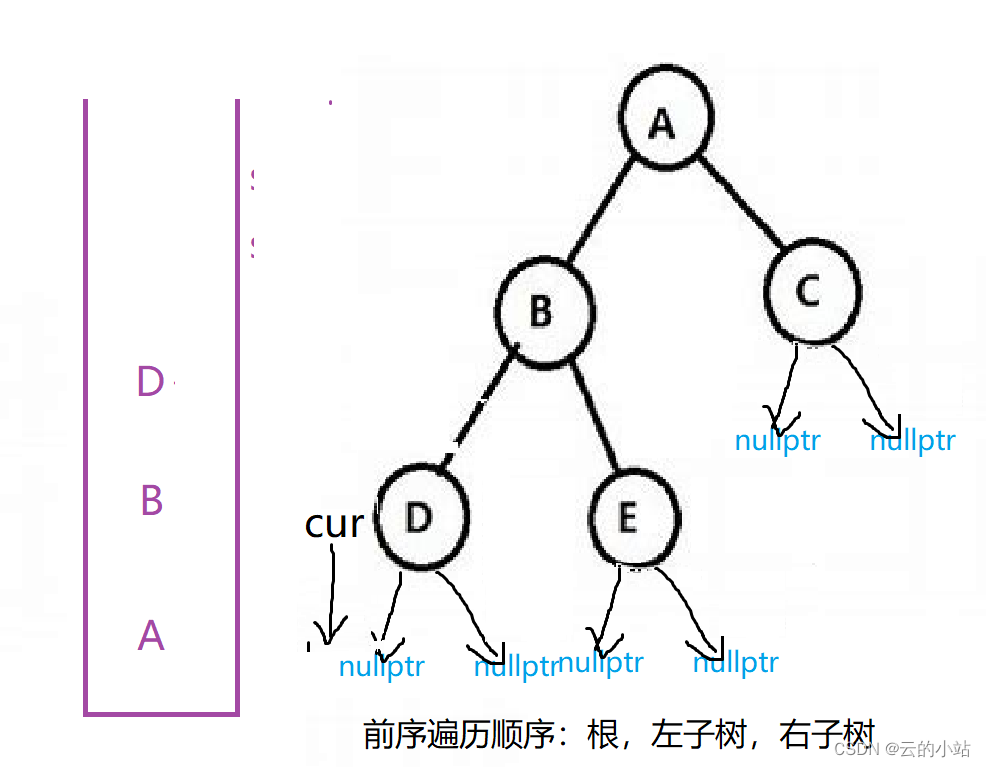
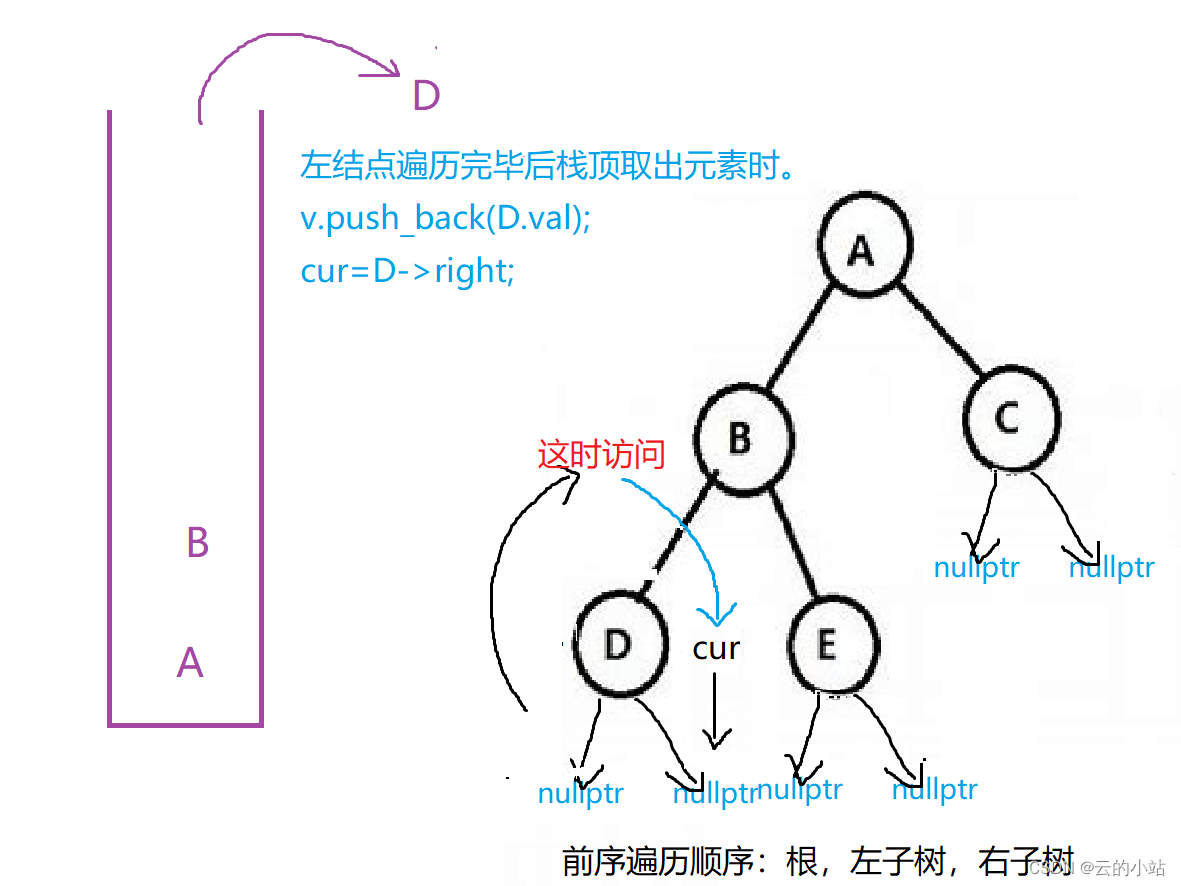
当访问到左树为空时就将栈顶元素拿出来并且删除栈顶元素，将拿出的二叉树根指针的右子树赋值给遍历指针

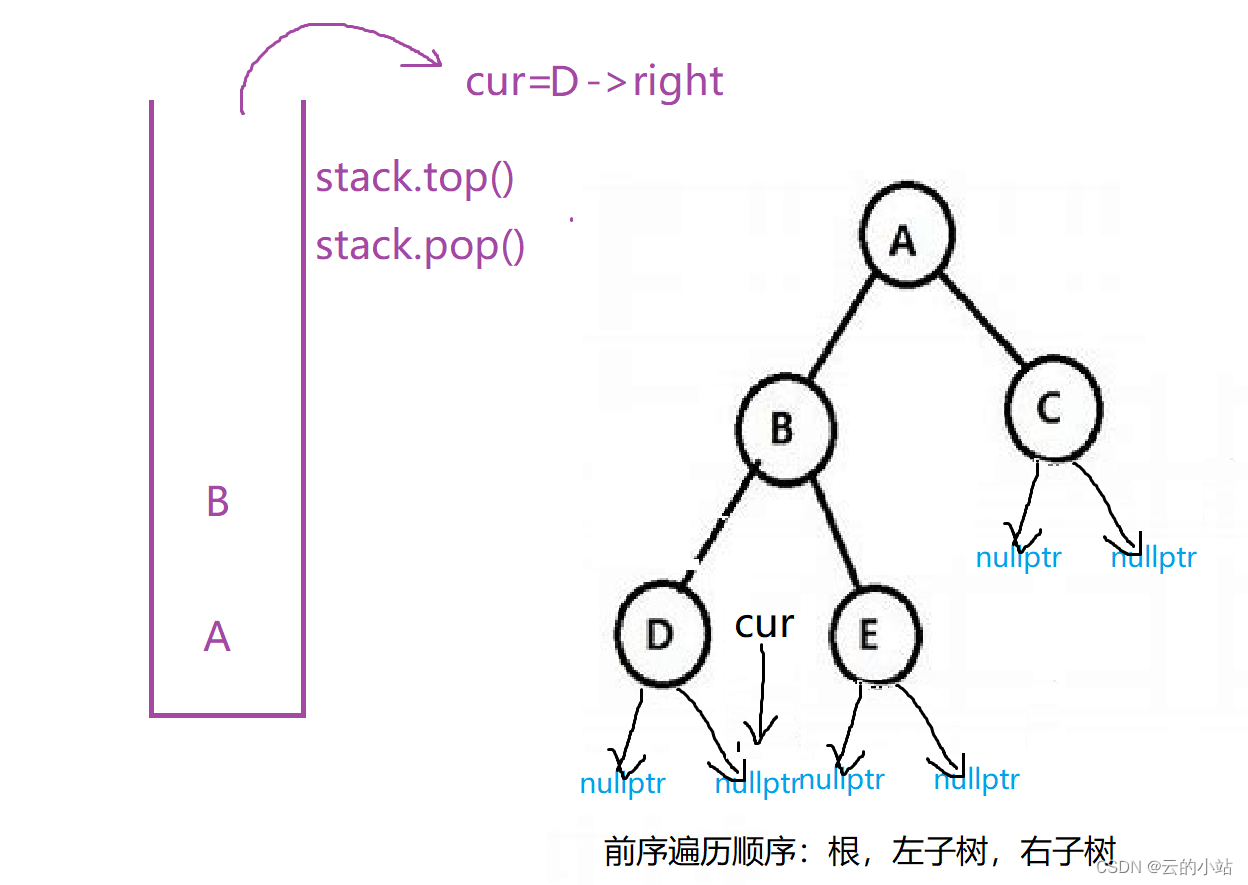
 cur遇nullptr时继续取栈顶元素并删除栈顶，右树继续赋值给cur

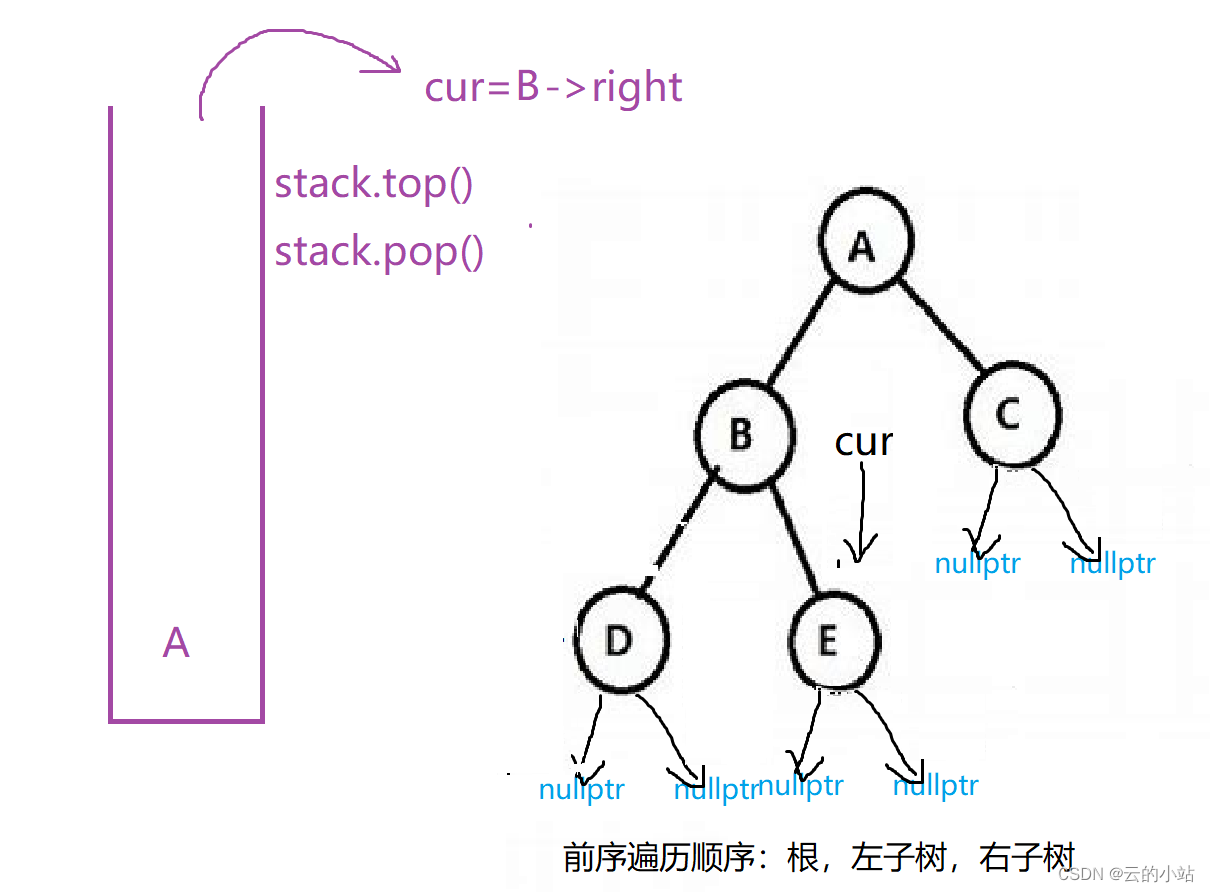
然后压入元素E，cur=cur->left

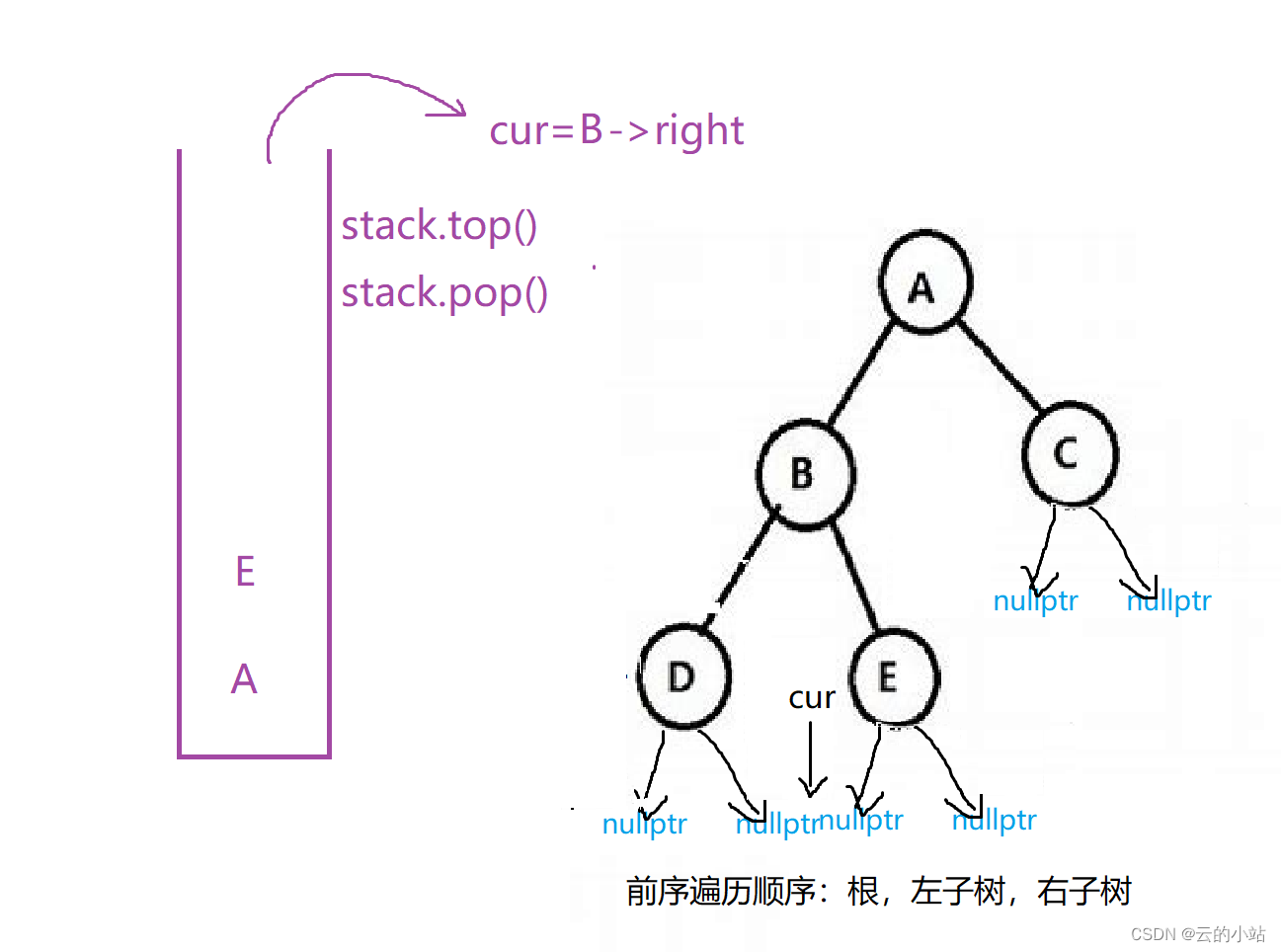
cur==nullptr结束循环，取栈顶元素，将元素的右树赋值给cur，并pop栈。  

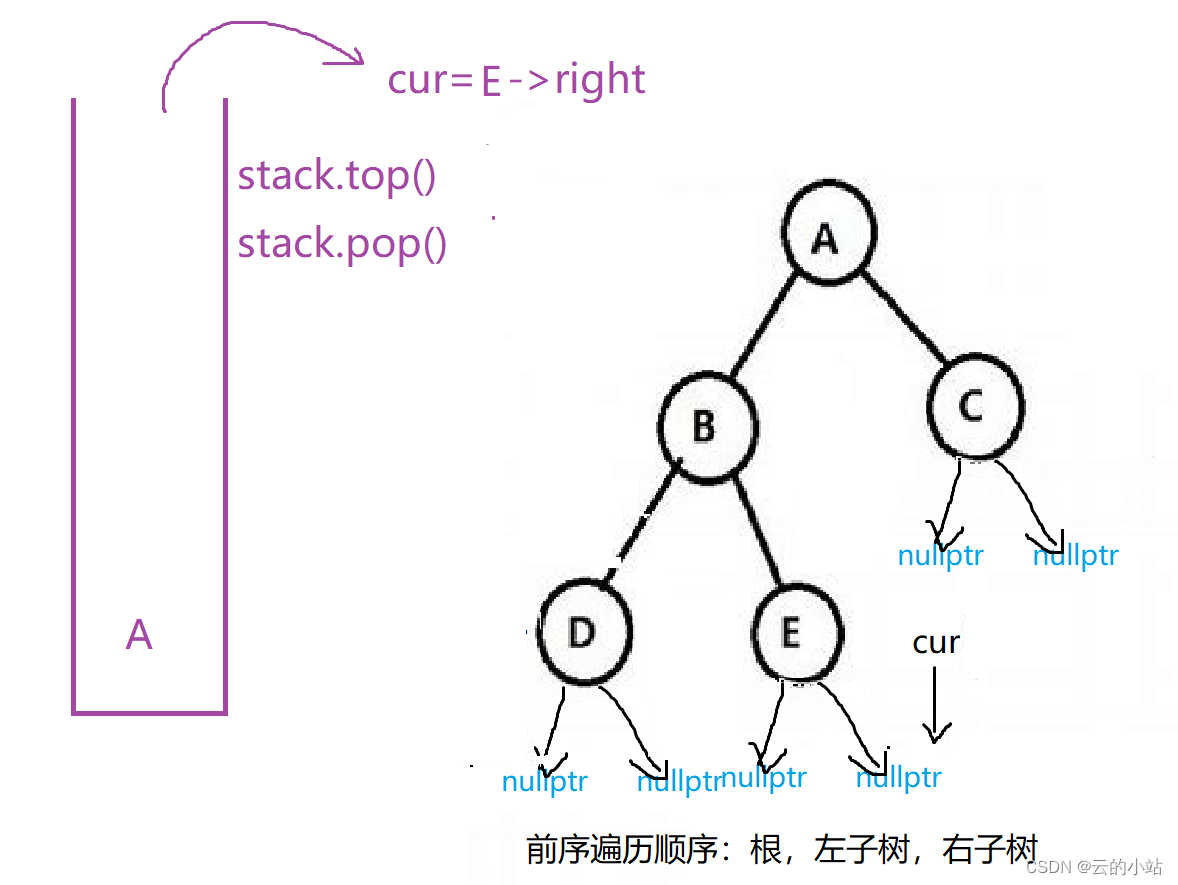
cur==nullptr结束循环，取栈顶元素，将元素的右树赋值给cur，并pop栈。  

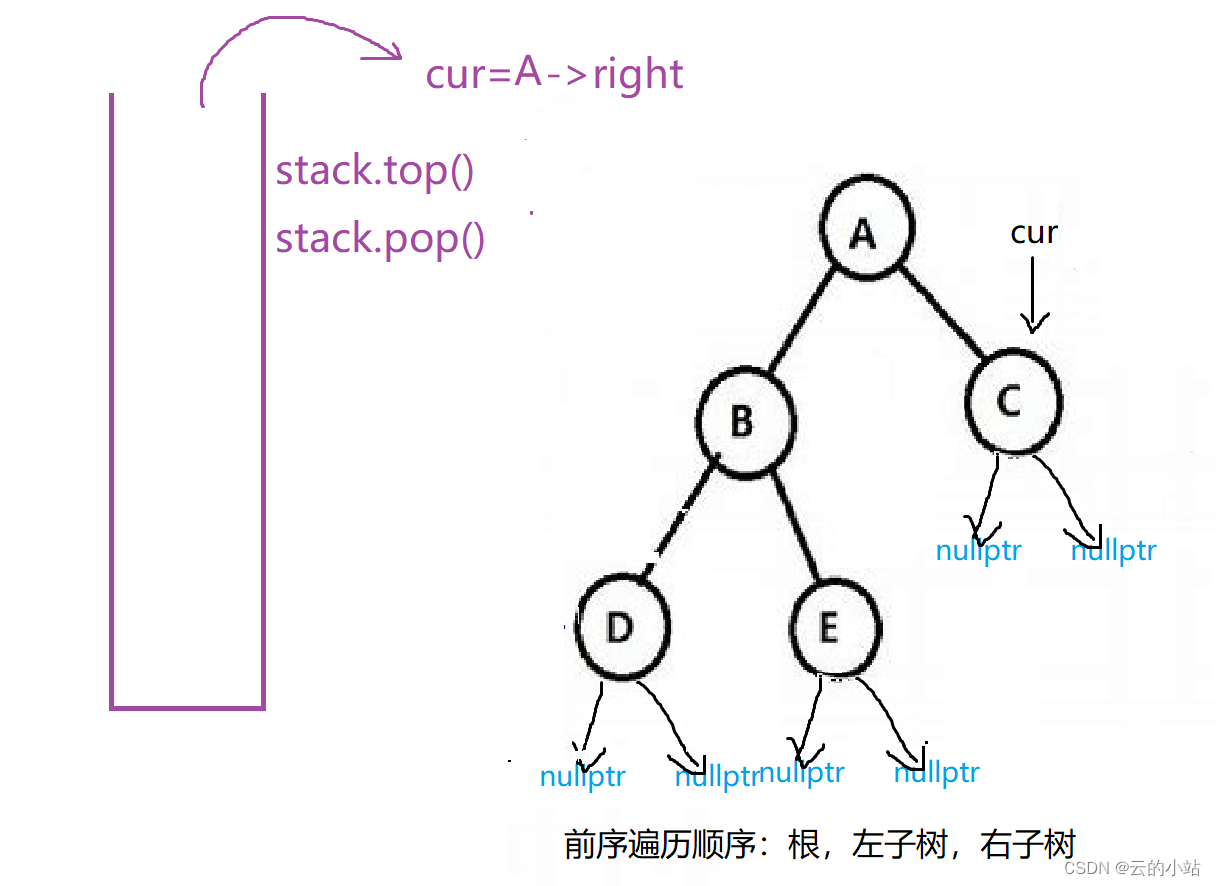
 最后访问结束后cur==nullptr，stack也是空栈。

 

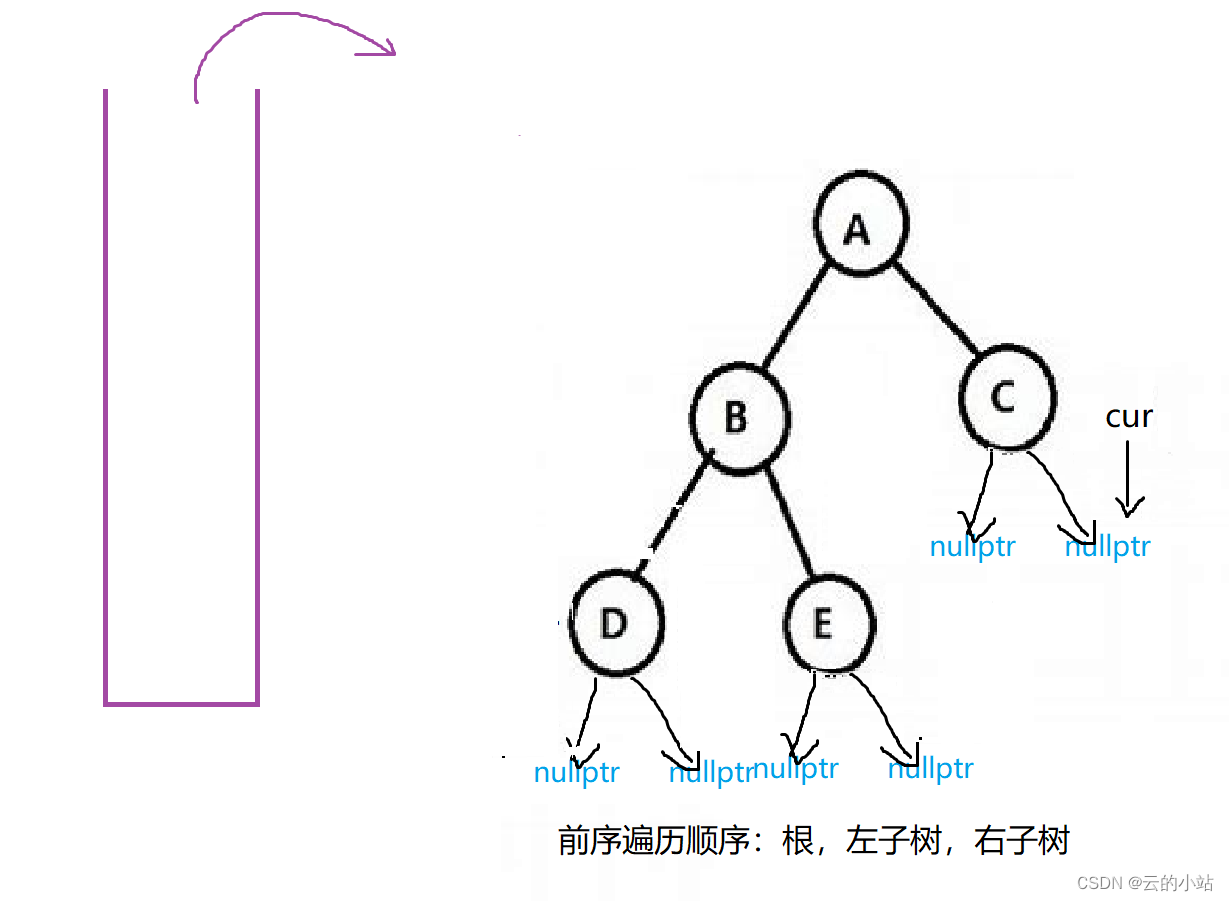
访问结束，退出循环。

查看代码：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode*cur=root;
        //只有栈空并且cur==nullptr才会退出循环。
        while(cur ||!st.empty())
        {
            将节点访问，并且移动到左子树
            while(cur)
            {
                //入vector就是对结点访问。
                v.push_back(cur->val);
                st.push(cur);
                cur=cur->left;
            }
            cur=st.top()->right;
            st.pop();
        }
        return v;
    }
};

中序遍历

中序遍历的迭代写法类似于前序迭代代码。改变访问位置即可，前序遍历都是来到一个结点先访问在去左子树，而中序就是子树访问完毕后再去访问根结点。在栈top时访问该元素即可。

看中序代码：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
    stack<TreeNode*> st;
        vector<int> v;
        TreeNode*cur=root;
        while(cur ||!st.empty())
        {
            while(cur)
            {
                //结点压栈，但是不访问。
                st.push(cur);
                cur=cur->left;
            }
            
            TreeNode* top=st.top();
            //取出栈顶元素后访问就是中序访问
            v.push_back(top->val);
            //访问后将top的右子树赋值给cur
            cur=top->right;
            st.pop();
        }
        return v;
    }
};

后序遍历（重点）

画图+代码理解。

    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode*cur=root;
        TreeNode*prev=nullptr;
        while(cur ||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
         //......

前面代码和中序遍历一样，但是我们加了一个prev指针，用来保存返回前的结点

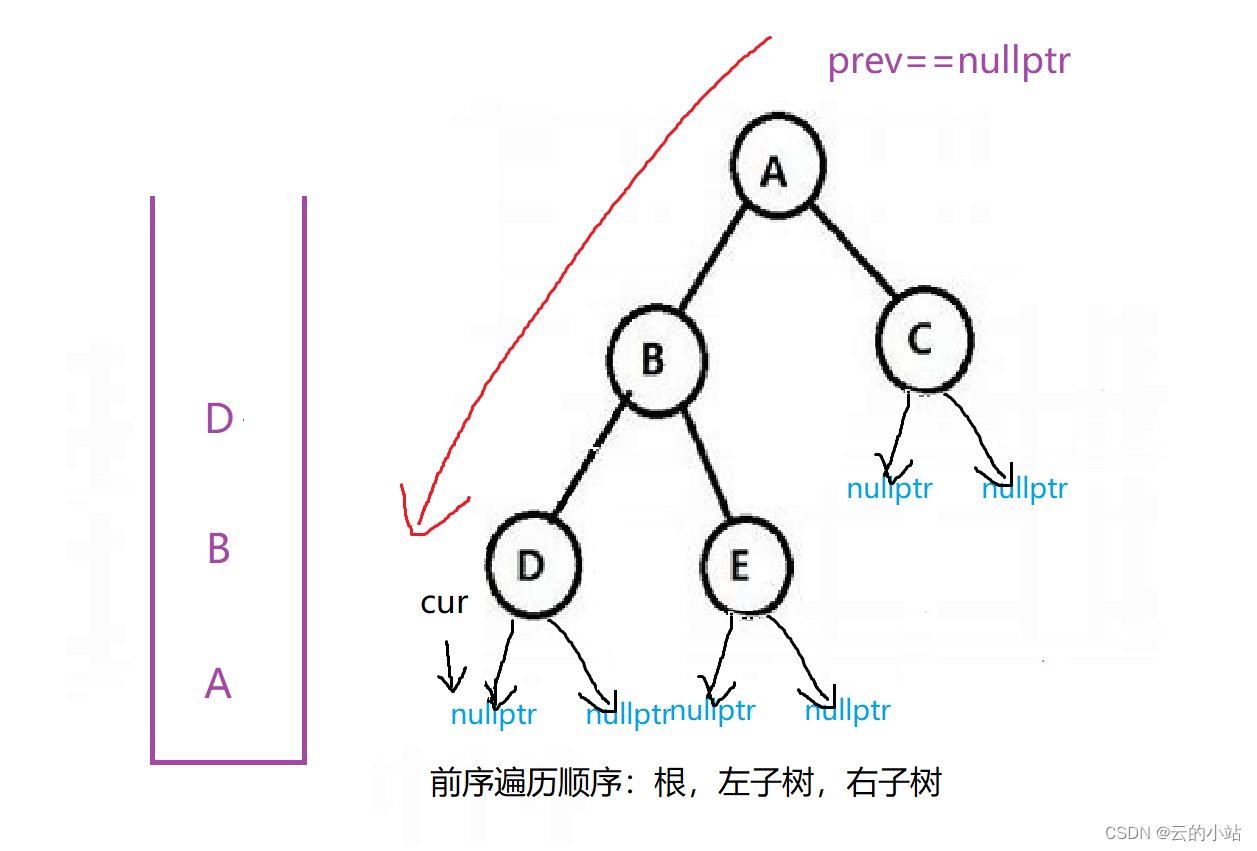
当我们访问到cur==nullptr是取栈顶元素进行操作。

 

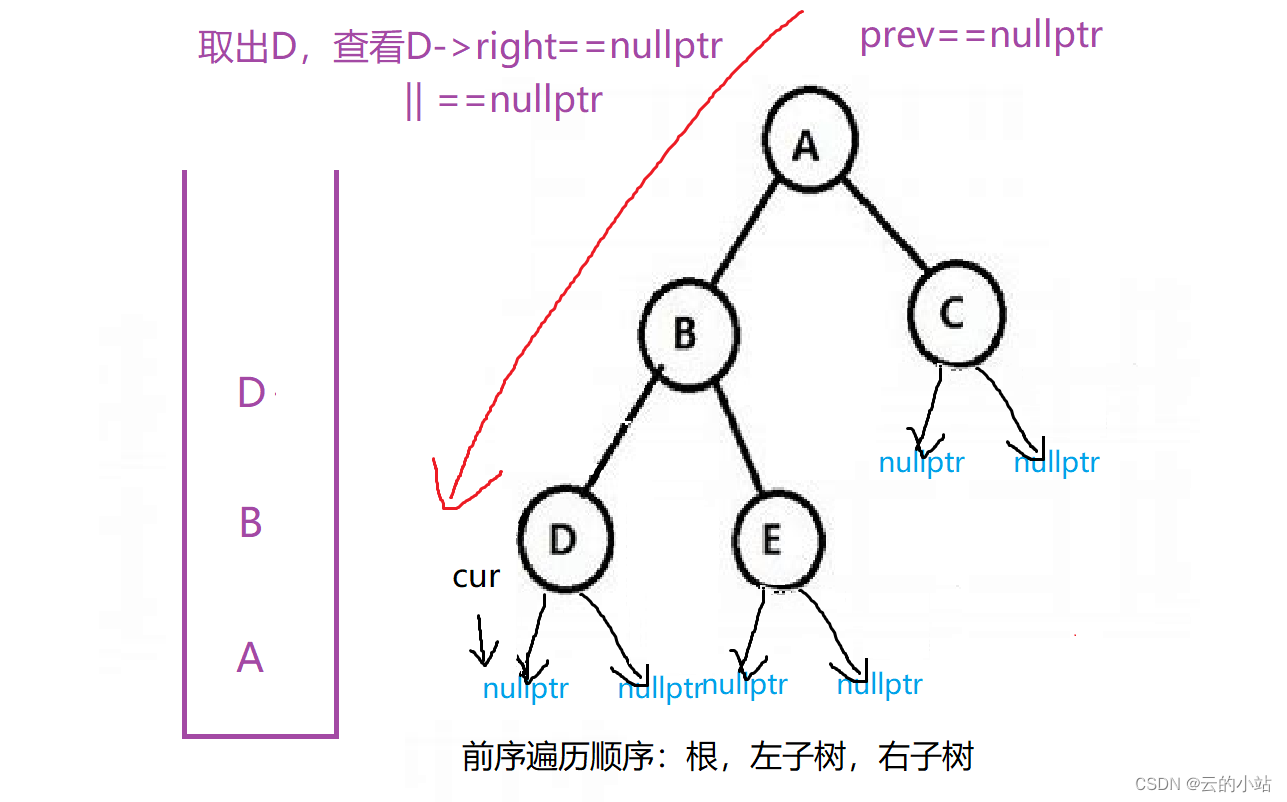
auto top=st.top();
if(top->right==nullptr||top->right==prev)
{
    v.push_back(top->val);
    prev=top;
    st.pop();
}
else
{
    cur=top->right;
}

 top->right==nullptr:当我们的结点的左边访问完毕后查看右边是否为空如果为空，就表示对结点数据访问。

top->right==prev：prev保存取出上一层取出栈顶的元素，我们查看他是否为这次栈顶结点的右结点，如果等于就意味着该节点的右子树访问完毕。

有点抽象吧？画个图，我也活动以下脑子。

 

 

 

 

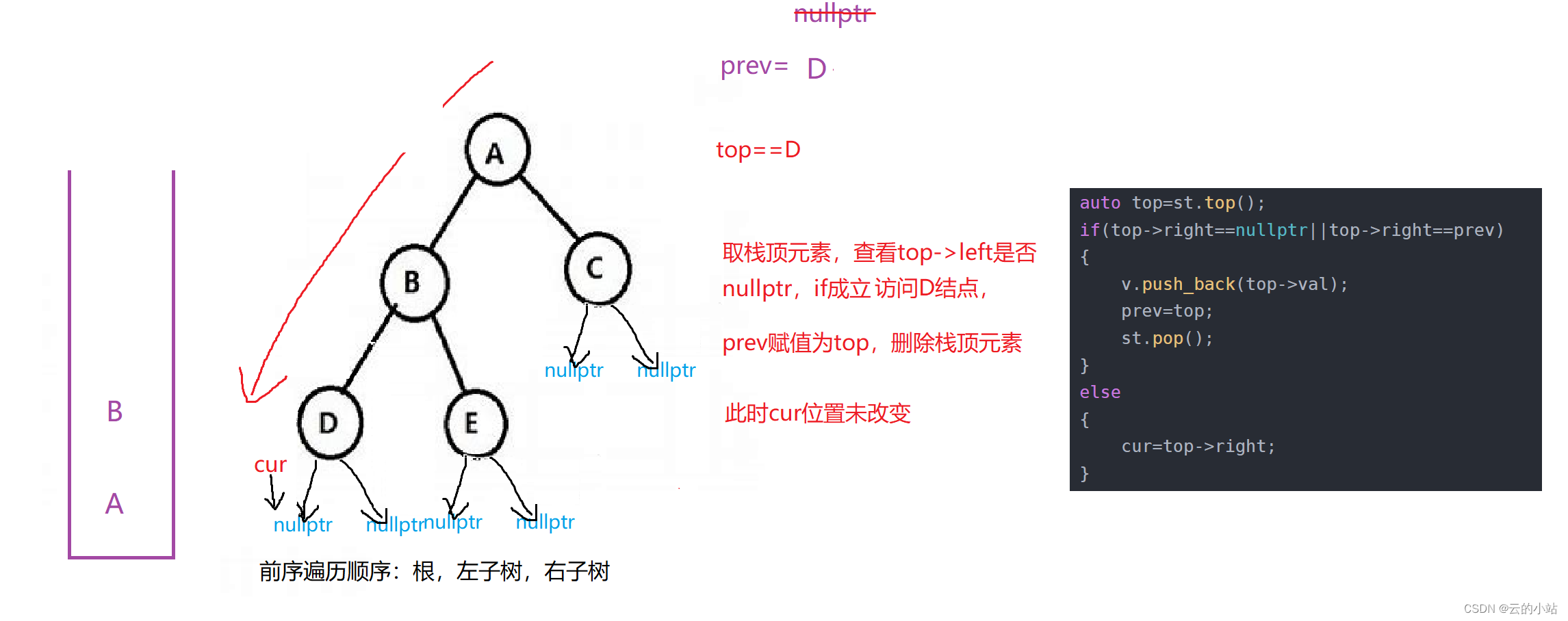
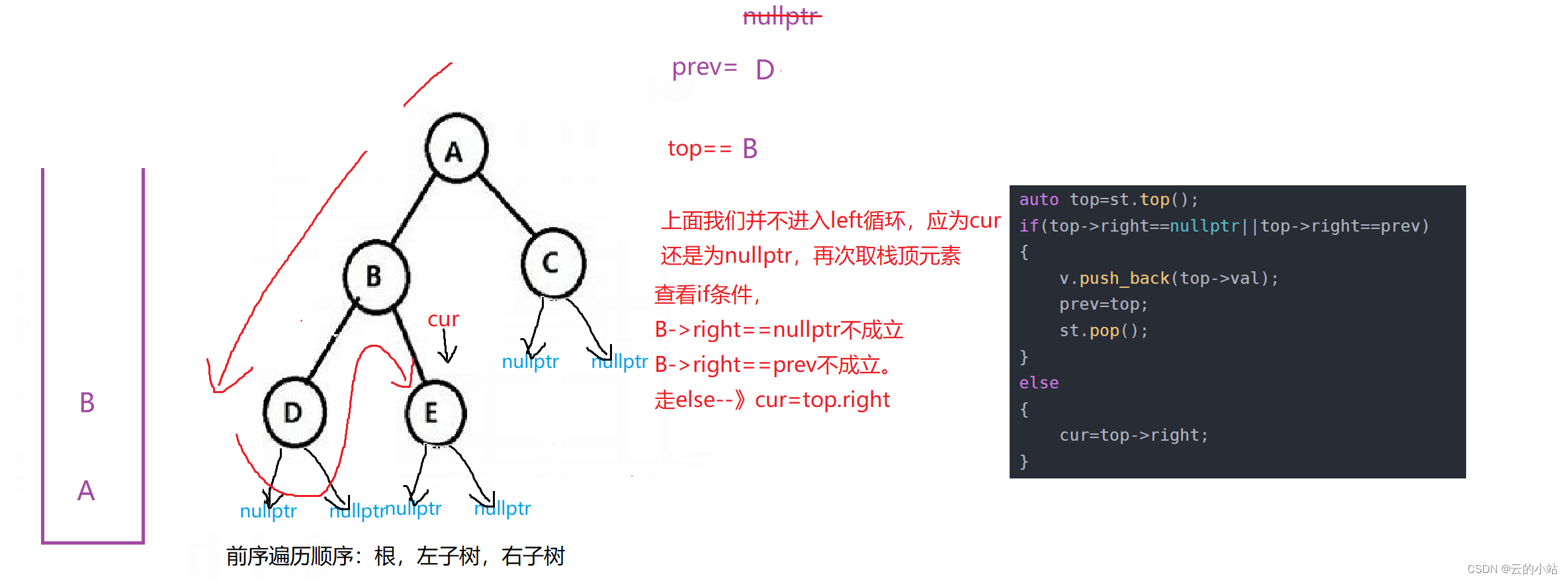
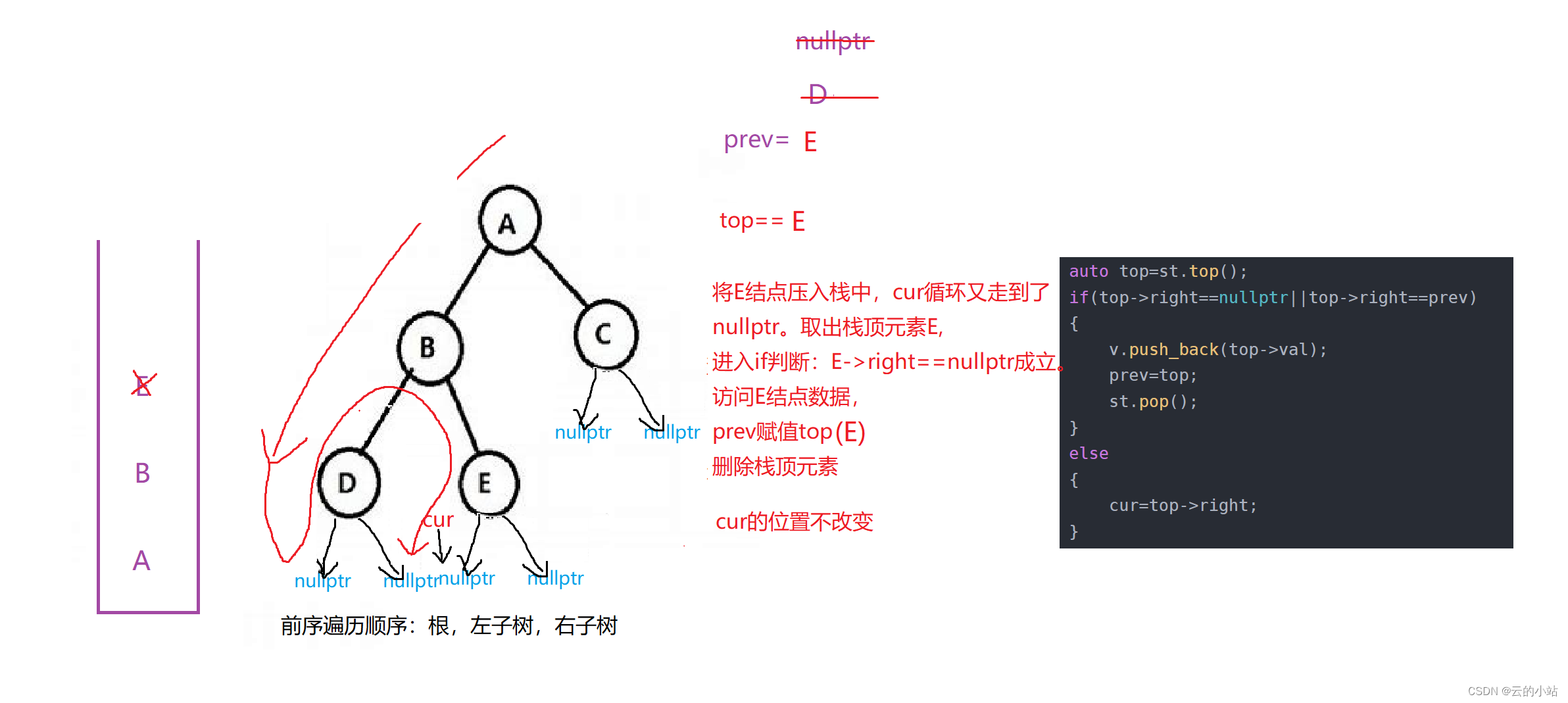
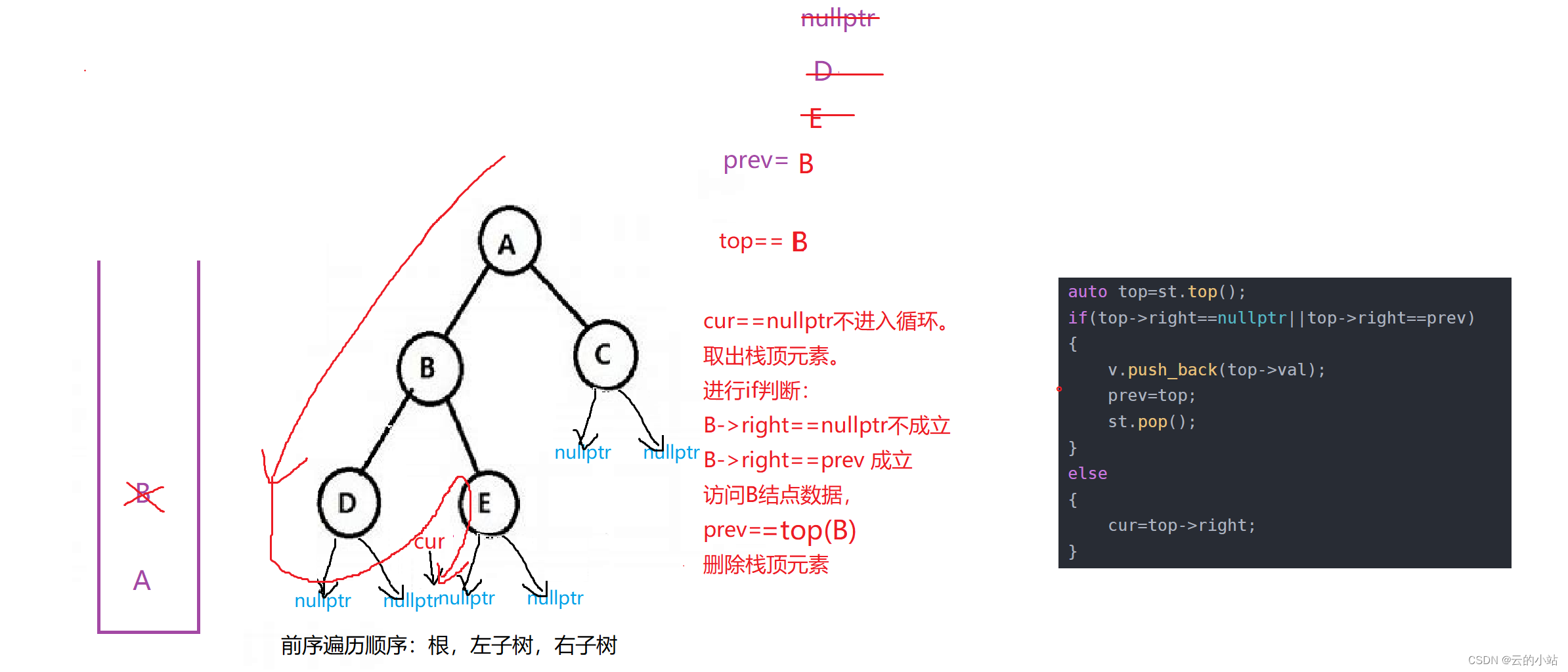
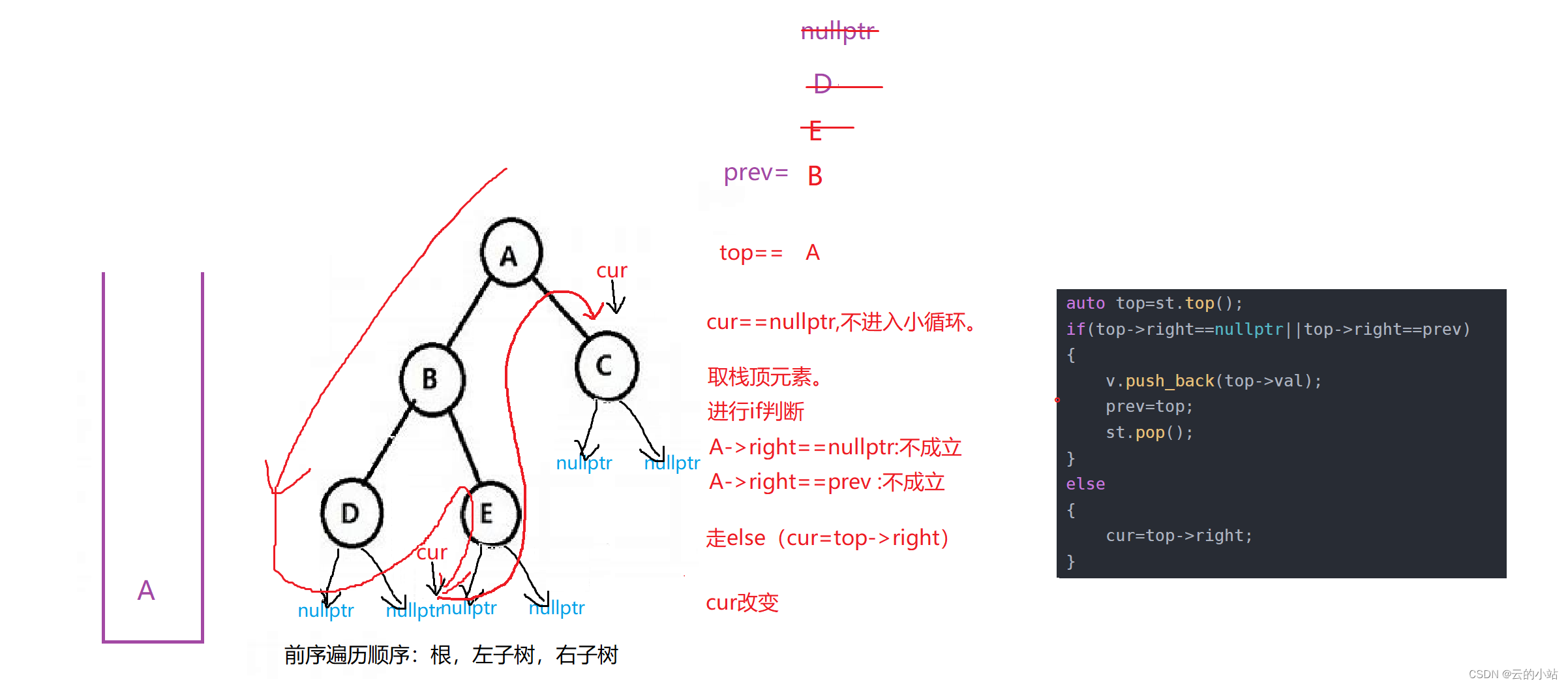
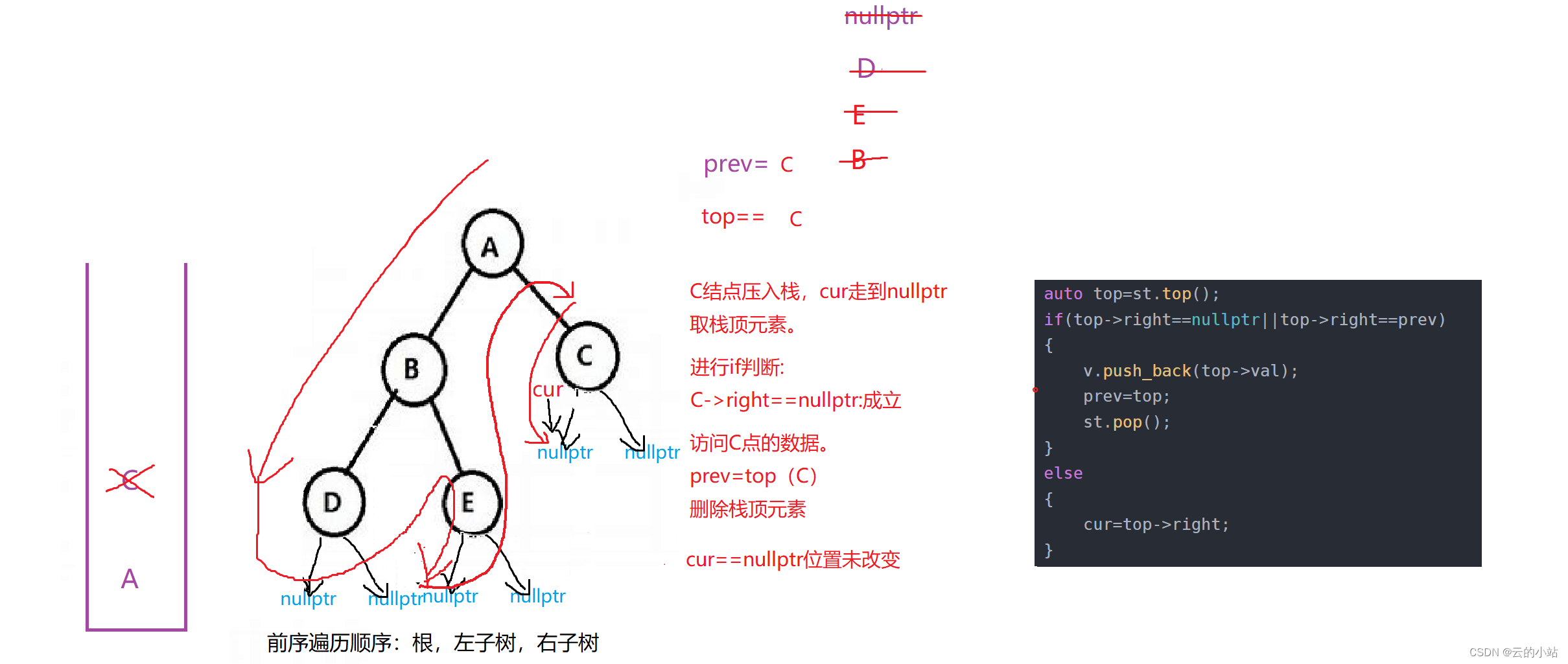
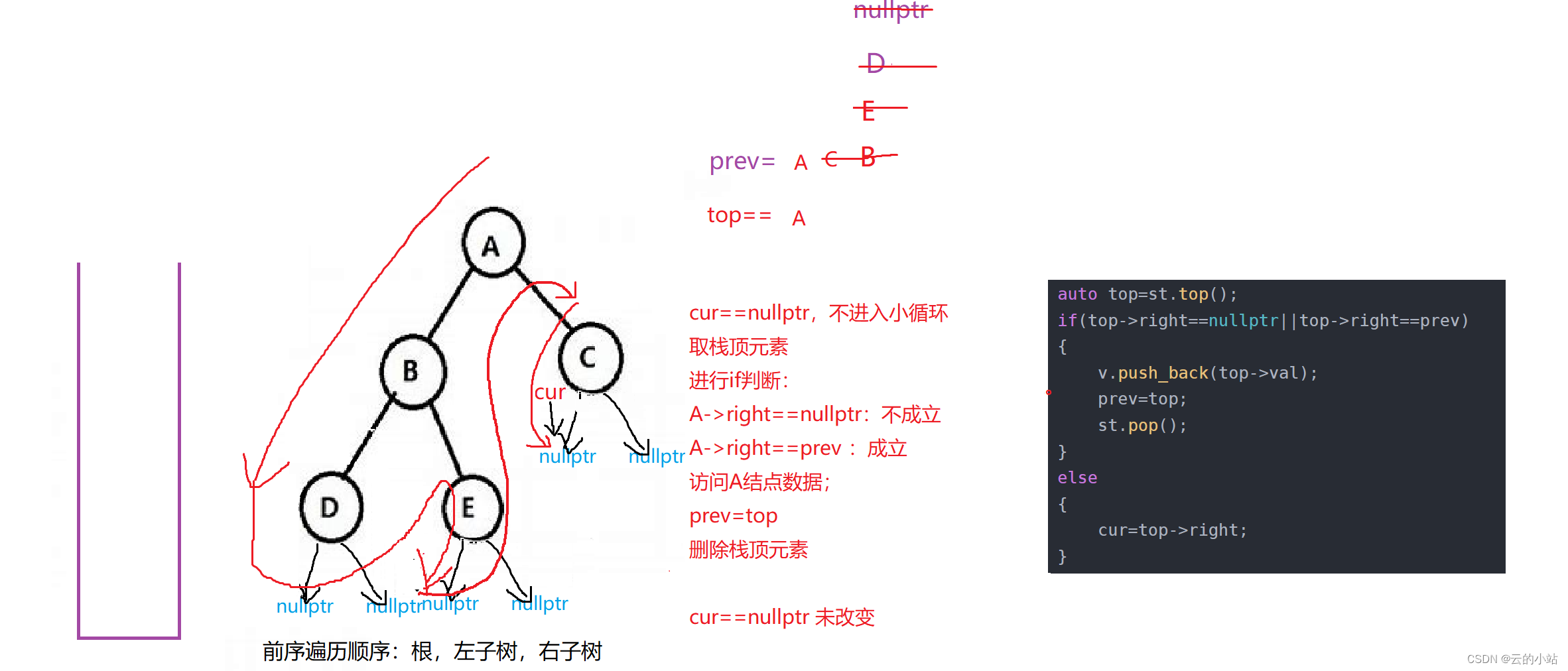 此刻！！大循环判断不成立退出循环

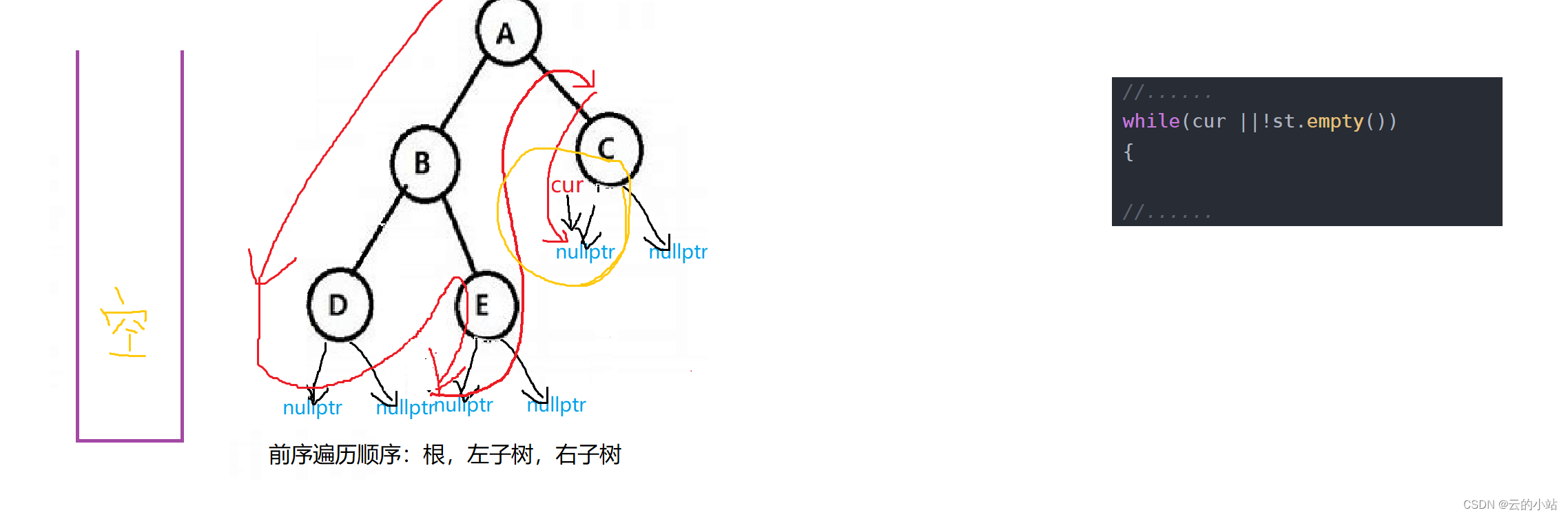
结束循环返回数据。树以后序遍历结束！！！

完整代码：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode*cur=root;
        TreeNode*prev=nullptr;
        while(cur ||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            auto top=st.top();
        if(top->right==nullptr||top->right==prev)
        {
            v.push_back(top->val);
            prev=top;
            st.pop();
        }
        else
        {
            cur=top->right;
        }
        }
        return v;
    }
};