ADC 读取电位器旋钮，用回差消除临界值档位跳动

news2024/11/15 21:43:52

就是比如，用电位器当旋钮做风扇调速，划分出10 个速度档位，对应10 个ADC 转换结果的阈值。如果直接比较阈值，当旋钮拧到临近阈值的地方时，ADC 结果的微小跳动会导致风扇档位在两个级别之间不停左右横跳，因此想到了利用回差来消除抖动。

回差原理

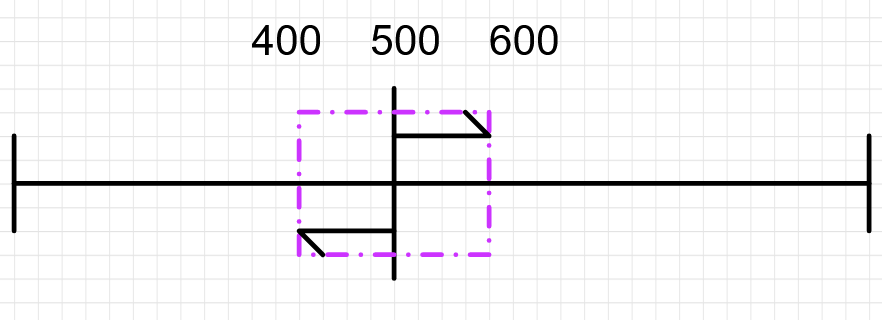
原理很简单，类似拿运放正反馈当迟滞比较器。如果只有两个档位，阈值是500，超过500 是2 档，低于500 是1 档，回差数值是100。那么如果当前位于1 档，电位器往大拧，想要调到2 档，ADC 的值要大于500 + 100 = 600。而如果当前位于2 档，要降回1 档，ADC 的值要小于500 - 100 = 400。

也就是说，阈值是动态的，和当前的位置有关。如果ADC 的值刚好是601，跳到了2 档，然后跳回1 档的阈值就瞬间变成了400，ADC 必须下降200 以上才能跳回1 档。同理，如果下降到400 跳回了1 档，再要到2 档就得上升200。所以只要ADC 的微小抖动范围不超过两倍回差，档位就不会跳动。其实这就是用一个区间替代了单一的阈值，然后原先跟阈值做的比较就变成了和区间上下界的比较。

在这里插入图片描述

回差实现

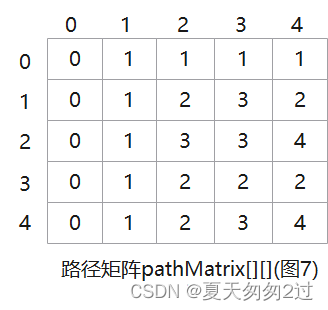
那么如果有很多档位，又该如何实现回差呢？也很简单，就是先保存当前的档位，判断阈值的时候，大于等于当前档位的所有阈值加上回差，小于的则减去回差，用图来表示就是下面这样：

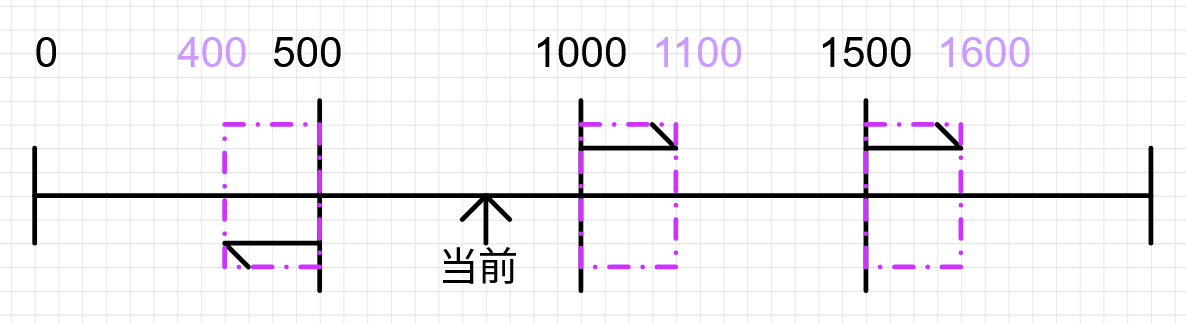
在这里插入图片描述
图中的意思是，假设ADC 的结果最大值是2000，从0 开始，把ADC 的取值划分为四个档位，进入四个档位的阈值分别是0、500、1000、1500，如果0 < ADC < 500，就代表第一个档位。实际程序中是只用上界来判断档位的，比如：

int 阈值[] = {500, 1000, 1500};

// 根据ADC 的值计算出对应的档位
int 计算档位() {
	for(int i = 0; i < sizeof(阈值); ++i) {
		if(ADC < 阈值[i]){    // 只用上界，也就是只用小于判断
			return i;
		}
	}
	return 3;
}

如果ADC 小于500，则为第0 档，否则ADC 肯定大于等于500，后面不用重复判断下界，只用接着判断ADC 是否小于1000。如果表查完了，说明ADC 大于1500，所以返回第3 档。用这种查表法的好处是：

省去复杂的乘除法。如果单片机不支持硬件直接算乘法，用查表可以省下调用乘法库函数的开销；
区间划分更灵活，可以方便的按实际需求做修正，实现不均匀的区间；
可以直观的实现回差，和上面的图对应；

也可以用累加：

int 计算档位() {
	int 阈值 = 500;
	for(int i = 0; i < 3; ++i) {
		if(ADC < 阈值){
			return i;
		}
		阈值 += 500;
	}
	
	return 3;
}

缺点就是不方便实现不均匀的划分。实际应用经常遇到非线性的传感元件，比如光敏或热敏电阻，可以用非线性的阈值表负负得正，给它修正成近似线性的。

然后按上面说的思路，在函数里加上对回差的处理：

int 阈值[] = {500, 1000, 1500};
int 回差 = 100;

// 计算ADC 的值对应的档位，需要输入当前的档位来计算回差
int 计算档位(int current) {
	for(int i = 0; i < sizeof(阈值); ++i) {
		int r = 阈值[i];
		if(i >= current) { // 如果是大于等于当前档位的阈值，就加上回差
			r += 回差;
		}
		else {  // 否则减去回差
			r -= 回差;
		}
		
		if(ADC < r){    // 再用叠加了回差的阈值判断档位
			return i;
		}
	}
	return 3;
}