前言

说实话，我不是很想上这门课，确实没什么大用，虽然我觉得这门课学一学也挺好，但是我觉得弄8个大实验就真的不太够意思，不如纯理论。

吐槽归吐槽，还有两天就要考试了，从现在开始我要把哈工大的课程刷完，写篇笔记，稍微刷点题，然后及格飘过。

虽然很多人说这个老师是念ppt，但是其实不然，ppt很复杂，你自己看还是有点麻烦，不如让老师给你指出顺序，这样也舒服，建议2倍速。

这课讲的确实不错，条理清晰，ppt也好看，果然群众的眼睛是雪亮的，听学校的课真不如课下听听这个。

概论

编译就是一个翻译的过程，将高级语言（源语言）翻译成汇编语言或者机器语言（目标语言）。

编译系统是一个很大的项目，从源程序到目标及其代码全部包揽，其中分为4部分，以C语言为例解释其作用：

1. 预处理器：.c变.i。处理所有的#号语句。比如#include语句（导入模块），处理宏定义#define
2. 编译器：.i变.s，编译系统的核心，编译原理课程研究的对象
3. 汇编器：.s变.o，此时机器代码段已经生成，其中的机器代码都是可重定位的（只有逻辑地址）
4. 链接器/加载器：链接器将.o代码段组合，加载器将完整的程序加载到内存中运行（转逻辑地址到物理地址）

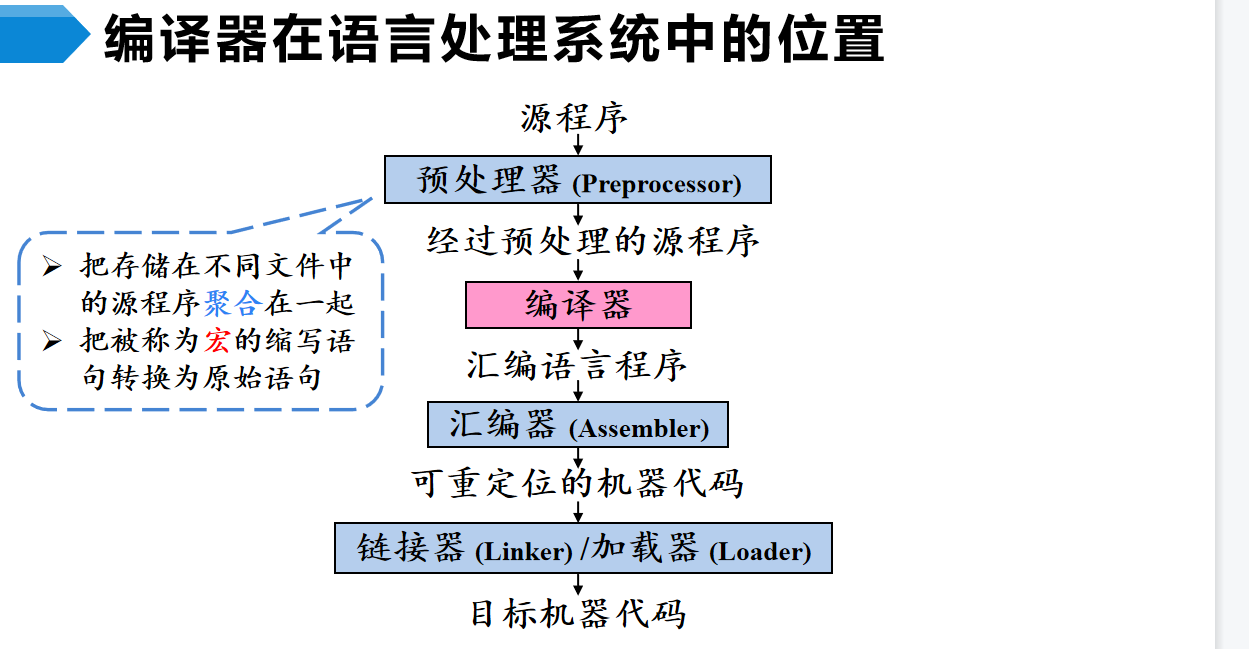
我们来具体研究一下编译器的编译过程，整体上分为两个阶段，先从源语言理解出语义，变成中间代码，然后再将中间代码转化为目标的语言。这两个阶段分别叫做编译器的前端和后端。

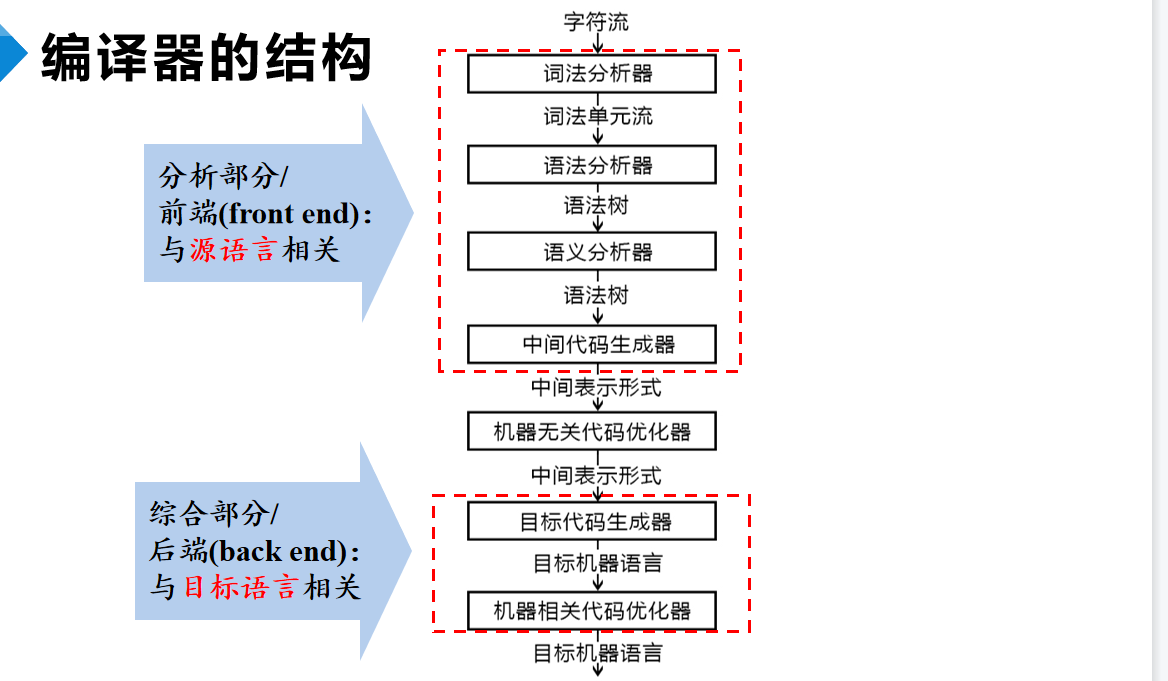
整体过程其实和人类的翻译过程是很像的：

词法分析 — 单词词性，孤立个体
语法分析 — 单词组合，构造短语
语义分析 — 连词成句（纠错），直译句义
中间代码 — 抽象提取，句义意会
代码优化 — 同义替换，翻译润色
目标程序 — 翻译结果，成品输出

下面来逐一介绍：

词法分析（Scanning）就是把一整个句子，切成一个又一个单词，确定单词的类型并且打上标记，变成token

一词一码的单词，只需要种别码就可以了，属性值可以不要，因为已经可以区分了。对于多词一码的，需要用种别码界定大类，然后用属性值确定内容。

语法分析（Parsing）将词法分析的结果加工，把词串成短语，以语法树的形式输出。

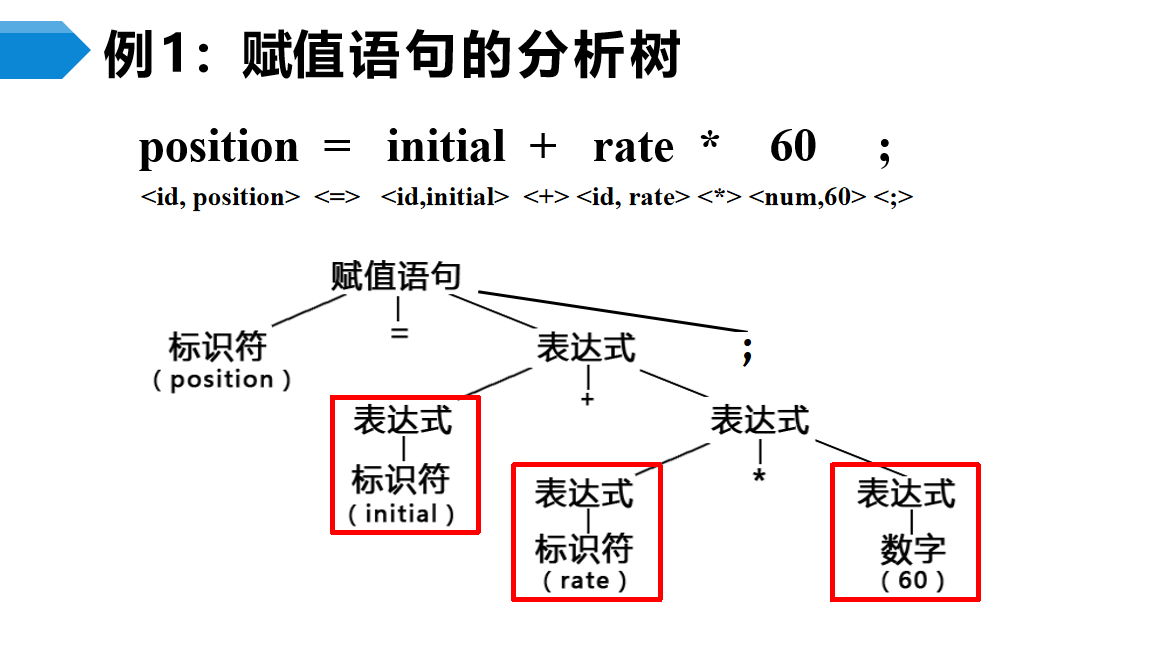
语义分析（Semantic）比较抽象。

什么是语义呢？TODO，我感觉程序说白了就是在玩各种变量，函数，那么语义就代表着我要把变量的各种信息以及函数的各种信息都提取出来，只要把这些东西搞出来，后面转化成机器语言就很方便了。

所以语义分析的一大任务是收集标识符的属性信息，标识符无非就是变量函数这些东西，收集他们的属性就是在搞清楚他们想干点什么。

最后这些东西记录在符号表里，之所以NAME字段是<符号表中地址，长度>的格式，是为了节省空间，毕竟长度不确定，统一长度难免浪费。

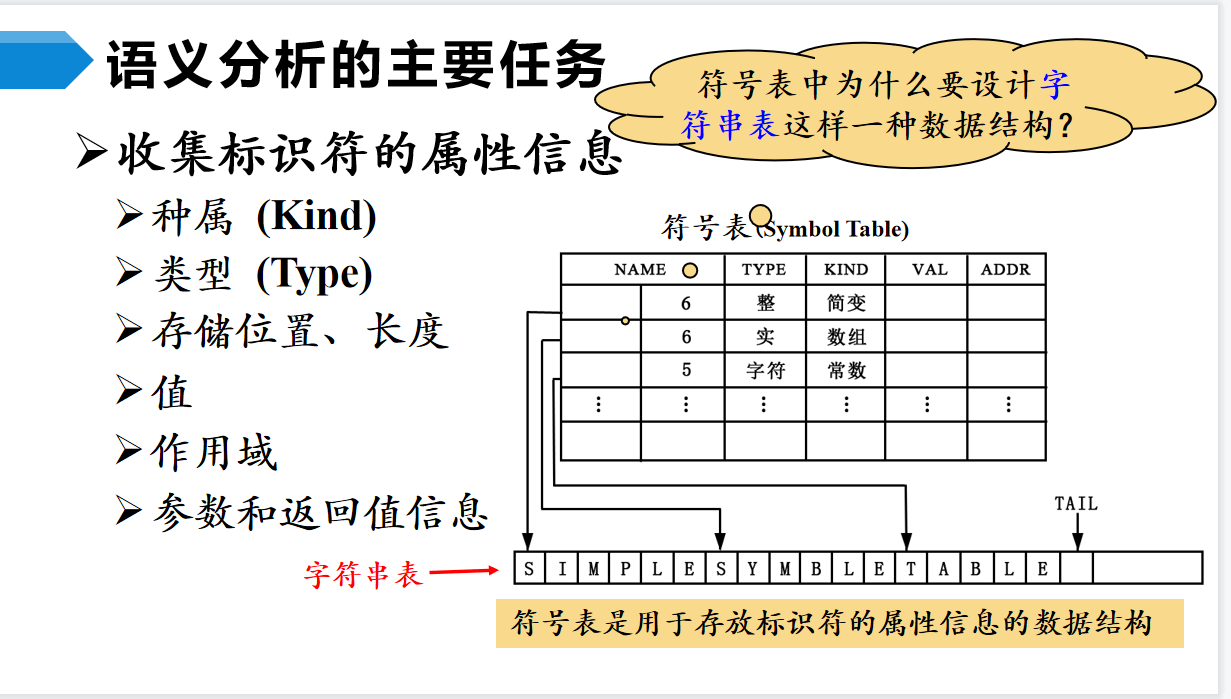
除此之外，语义分析还要做最后一步的正确性检查，确保在进行代码生成前没有错误。

中间代码生成（IC-gen）。语法树其实已经是一种中间形式了，但是这种结构还是更适合人看，机器更喜欢一条一条的代码，所以ic-gen阶段将语法树转变为一条一条的中间代码，后面生成目标代码可以直接对照生成。

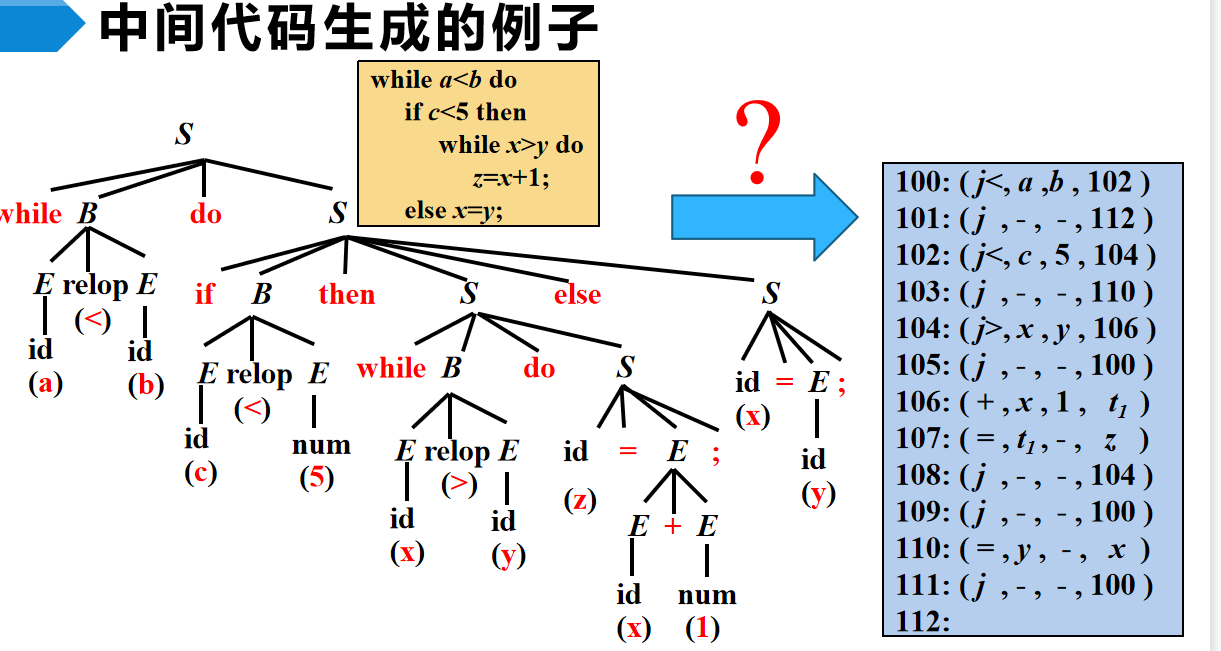
中间形式叫三地址吗，代表一条指令最多有三个操作数，一般用四元组表示，多出来的这个1指的是操作符，很像汇编语言。

给一张表，下面的地址码使用标志符表示的，不是说地址吗？这是因为，符号表里面已经记录了标志符到地址的映射，所以用标志符=用地址。

总结一下四元组表示的规律：

1. 有赋值操作的
   • 一般是两个源操作数作为2，3分量，不够就空开，目标数作为第4分量
   • x[i]这种比较特殊的目标，以i作为目标数
2. 无赋值操作的
   • 一般都只有一个目标数
   • call比较特殊，只有两个源操作数

目标代码生成（nc-gen）是吧中间形式映射到目标语言。一般是将中间代码映射到目标代码，有的人也会把语法树映射成目标代码，但是及其受限，还是要一步一步走才好。nc-gen的关键是寄存器的合理分配。

代码优化无非就是优化空间或者速度。

语言与文法

基本概念

字母表

字母表：符号的集合，一个语言中最最基本的元素集合。注意，字母表里面不一定只是一个一个的符号，也可以是串，后面就会看到的。

字母表的运算如下：

1. 乘积。本质上就是集合乘积，即笛卡尔积
   

2. n次幂。幂的定义就是连续乘积。直观理解，就是长度n的字符串集合。照这么理解，其中0次幂的结果是空串集（长度为0的字符串集合），而不是空集，也就很合理了。
   

3. 正闭包。这个也是离散数学上的概念，直观理解为任意长度的字符串集合，正即不包含空串
   

4. 克林闭包（Kleene closure）。相比于正闭包，多了一个空串。
   

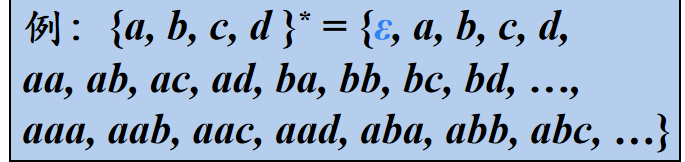
串

字符串是一个老生常谈的概念，其实就是字母表上字符的任意有序排列组合（包括空串），用规范的语言说，就是字母表克林闭包的元素。

字符是语言中最基本的元素，那串就是语言中最常用的基本元素，字符本身其实也算是一种串，串是一个更大的概念。

来看下运算：

1. 连接。就连起来而已，由此引申出前后缀的概念，这是相对的，有前缀就有后缀，甚至于空串都可以作为前后缀。
   
2. 幂。n次幂=连接n次
   

字母表与串的联系

其实到这里你就可以发现，这两个东西似乎有一种本质的联系，说白了就是集合和元素的关系。

你会发现，串的连接运算与字母表的乘积对应，串的连接结果$\in$字母表乘积。串的任意组合对应着字母表的乘积组合，任意串对应着字母表的克林闭包。

其实就是元素和集合的关系啊，有趣。

文法

什么是文法？用抽象一点的话说，就是表示了基本符号如何构成语法成分，以及语法成分如何进一步组成更宏观的语法成分。

蚌埠住了吧，直接看例子吧。对于自然语言，基本符号是单词，语法成分是短语和句子。倒数4个介绍了基本元素如何构成语法成分，而前几条介绍了语法成分如何组合成更宏观的语法成分。

想一想语法树，是不是一层一层的，我们这个构成其实也是从下到上一层一层的。

下图仅仅是针对自然语言的，基本符号是单词，语法成分是短语和句子，如果是针对单词来说，那么基本符号就是字母，语法成分就是单词。

为了便于计算机处理和理解，我们用数学语言（形式化语言）去描述文法。总的来说，一部文法规定了一个语言的各种成分，以及转化规则：

1. 终结符对应基本符号
2. 非终结符对应语法成分
3. 产生式集合P对应这些成分之间的转化关系
4. 开始符号S对应最大的语法成分，所以开始符号归属于非终结符也是很合理的。

一部文法的元素集合其实在产生式里面就可以看出来，所以不引起歧义的情况下，甚至只写P都可以。所以我们重点研究一下产生式的表示：

这是最基本的写法，左边到右边是一个箭头，从左到右是分解，从右到左是合并。

P还可以继续简化，相同左部的产生式可以合并为一个，右边用|隔开，代表或，右边的每一项都叫候选式。

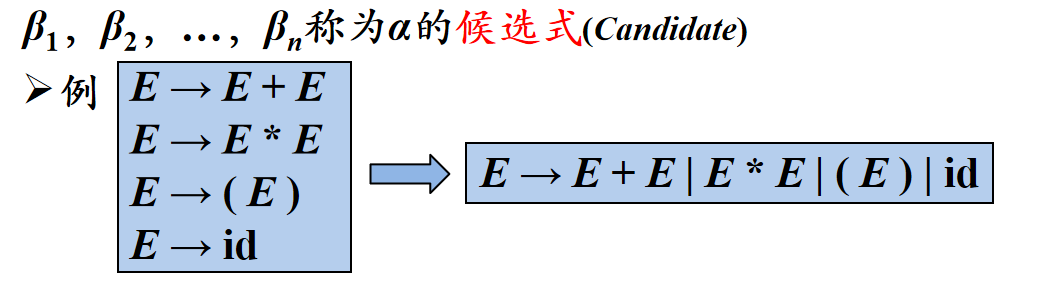
最后说下符号约定，好复杂，我感觉不用记那么多，后面慢慢就都记住了，所以这里只把基本规律放出来：

语言

推导和规约

什么是语言？此处直接给出定义：句子的集合

听起来有点像字母表，其实字母表也算是一种很简单的语言，而我们的语言集合，可以是无穷的集合，因为语言集合是从文法推导出来的，可以说，文法与语言是对应关系。

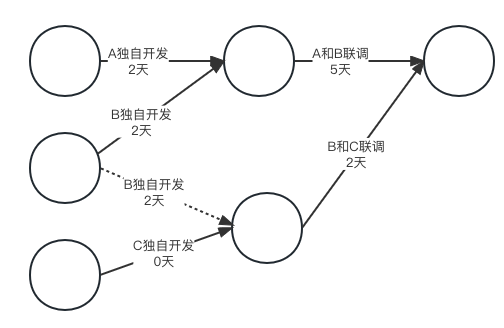
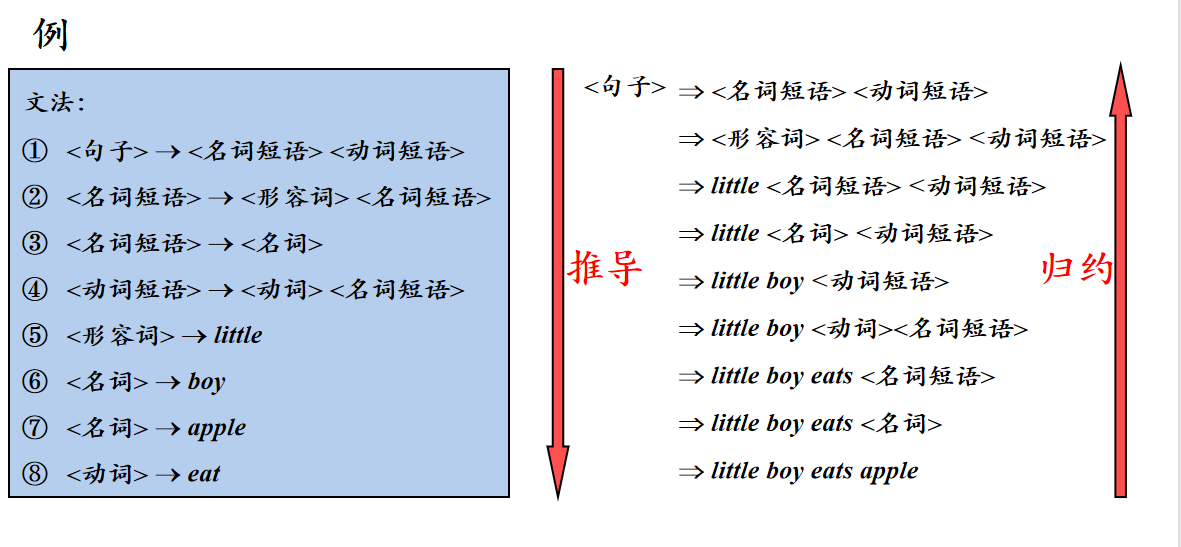
如何判断一个句子是否属于一个语言呢？还是要着眼于文法。一条文法，从左到右是分解，我们这里叫做推导，从右到左是合并，我们叫规约。

推导分为0步（没推导），1步（直接推导），n步（n步推导）

直接看例子吧。

句型与句子

我们说，终结符构成的串就是语言的一个句子，那我们在推导过程中产生的中间形式，里面又有终结符，又有非终结符，甚至全是非终结符，这又叫什么呢？句型

句型是比较抽象的，不具体的，所以就叫“型”，而句子就是一个完全的终结符串，句子也可以理解为特殊的句型。

语言与字母表

回归语言的定义，语言和字母表的元素都可以是字符串，那他们到底不同在哪里呢？本质在于，字母表是我们直接给出的集合，而语言是通过文法推导出来的。

所以我们说L（G）是文法G生成的语言L。给定一部文法，很有可能生成一个无穷集合，这就是用有限的文法表示无穷的句子，这就是语言的本质，用元素+规则表达无穷的组合。

我们来具体举几个例子。下面这部文法表示的是标识符，4条文法就表示出了标识符这个语言，而我们知道，标识符是无穷的：

1. L和D可以直接指向终结符，分别代表字母和数字
2. T总的来说，表达的意思就是L和D的任意组合，只要不是空串就行
3. S=L或者LT，这告诉我们标识符一定要以字母（L）开头，剩下的部分字母数字随意组合就好（T）

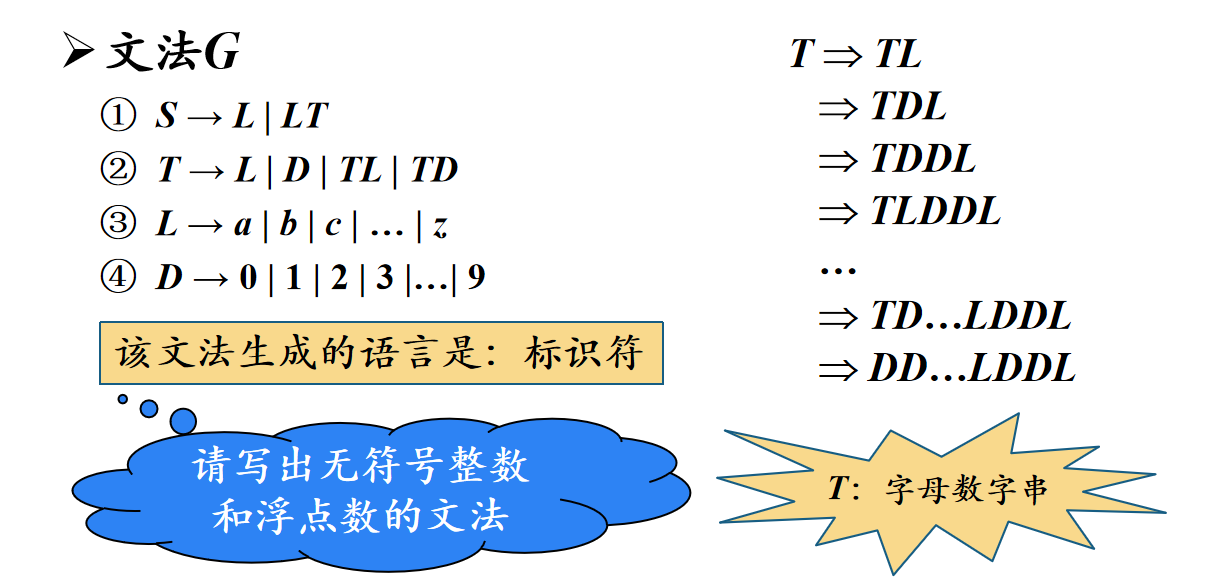
最后再重申一下语言和标识符的关系，区别仅仅在于怎么生成的，他们从成分上来说，其实是一样的，或者说字母表本就是一种语言。由此，运算其实是可以套用的，甚至可以把字母表通过语言的运算转化成更复杂的语言：

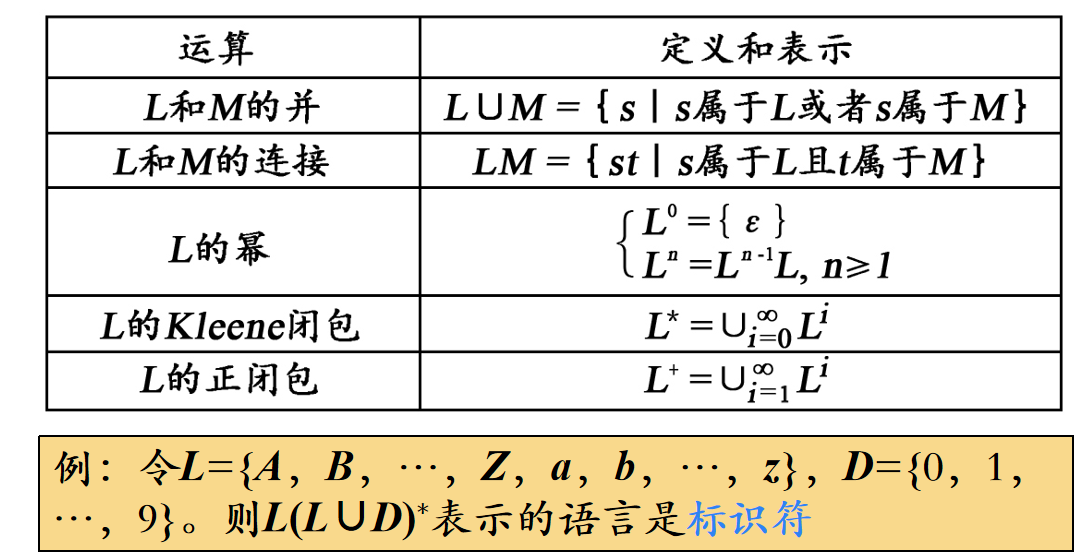
由此，串的运算，集合的运算，文法的推导，这三个东西其实是统一的。

文法的分类

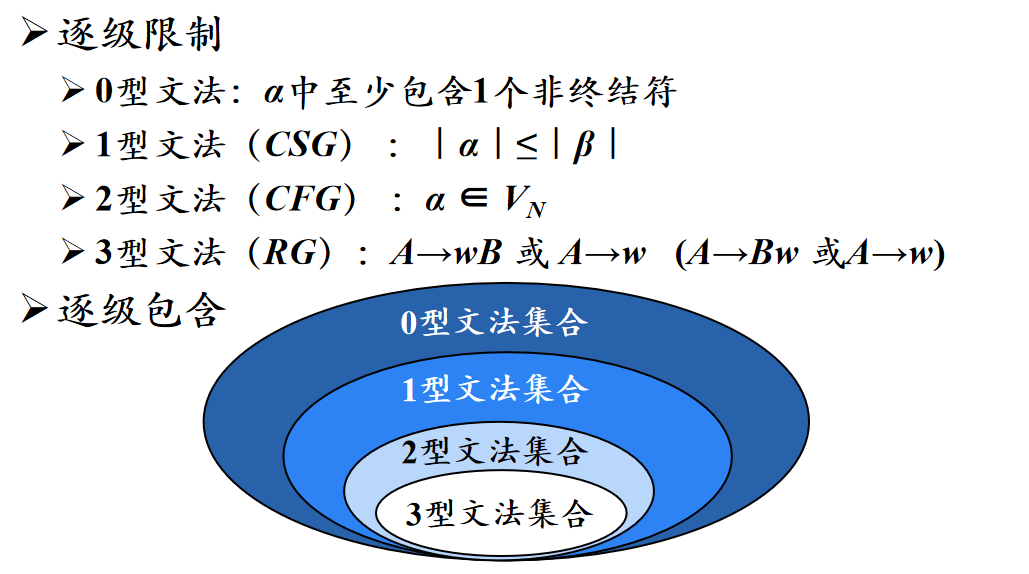
0123四类文法，自由程度依次递减。

0型文法就是我们前面用的文法，叫做无限制文法，高度自由，左边只需要有一个非终结符就行了。

这是最基本的要求，毕竟文法从左到右是推导，你左边要是没有东西（非终结符）可推导，这也说不过去，所以虽然高度自由，但是至少得有一个非终结符。

1型文法叫上下文有关文法（CSG），在0型文法的基础上，保证上下文不变，总长度只增不减。

上下文不变还是比较好实现的，而为了保证总长度只增不减，CSG生成式的右边不能有空串。

2型文法叫上下文无关文法（CFG），是基于1型文法的。

看似有关和无关冲突，但是如果我们限制上下文为$ϵ$，1型文法就会变成2型文法（不考虑右边为空的情况）

2型文法除了上下文为空以外，相比于1型文法，右边是允许空串的。

一般来说，我们写的文法更像是2型文法。

3型文法叫正则文法，也叫线性文法，分为左线性文法和右线性文法。

之所以叫线性文法，是因为每次推导只会增加1的串长。左右代表着字符串的增长方向，比如右线性文法，增长方向和非终结符的位置一致，就是右边。

正则文法和正则式对应，我们平时编程语言中会接触很多这个东西。

最后，如果不考虑1型文法右边不允许空串，那么0-3型文法就是逐级限制的。

CFG的分析树

前面我们知道，我们一般都是用2型文法的，所以就针对CFG研究一下它在编译过程中的表示。

一颗CFG分析树有三种节点，分别为根节点，内部节点，叶节点。

把所有叶节点排起来，直观看这些叶节点整体就是一棵树的边缘，这代表了一个树的产出

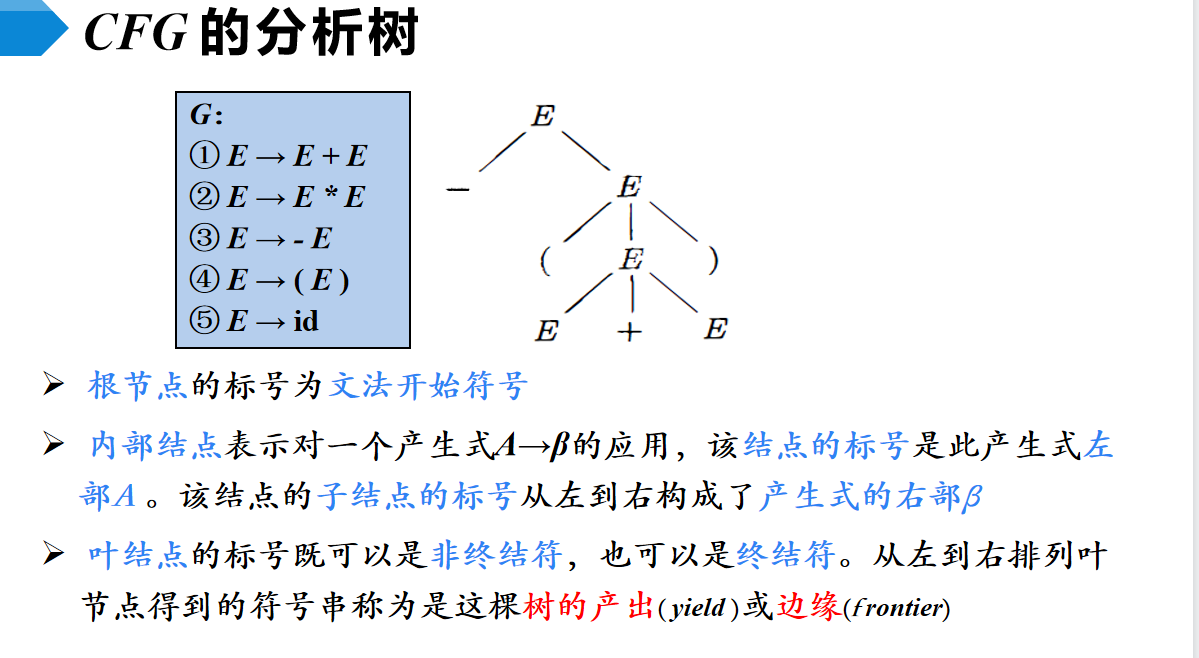
给定一个推导，推导的过程中，句型会不断变长。对应到树这里，给定一个根节点，每推导一次，树就向下生长一点，边缘/产出就会增加，推导的过程就是树不断变大的过程。

所以可以说，每个句型都可以对应一颗分析树

注意，叶节点不一定是终结符，这说明我们的推导不一定非要推导到没有非终结符为止，提前停下来也可以，也算产出。

下图中，该句型有3个短语，其中，有一个是直接短语。

因为产生式是一对多的，就是一个左部可能有多个右部，所以只能说推导出来的右部一定是直接短语，不能说某一个右部就是直接短语。

直接短语一定是当前句型可以推导出来的右部，随便给一个右部，不一定是当前句型能推到出来的，可能是另一个句型的直接短语。

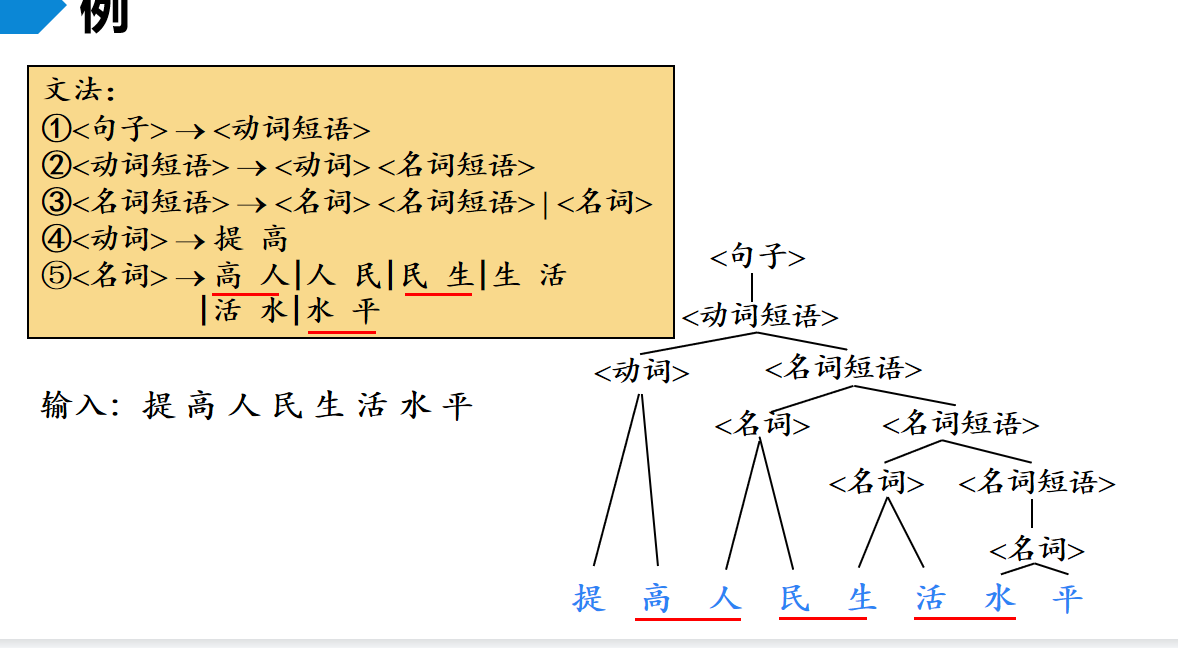
最后说一下二义性，一颗语法树代表一个语法结构，如果同一个句型可以得到两颗不同的语法树，计算机就会出现理解的歧义，计算机中不允许歧义出现。

对于一个CFS，没有一个充要条件可以判断二义性，但是有充分条件可以判断二义性。

如果出现二义性，解决办法就是修改文法。