Gurobi解决优化问题

news2025/1/10 16:13:01

Gurobi1介绍

Gurobi是一种优化软件，用于解决各种数学规划和整数规划问题。它提供了高性能的数学规划求解器，可用于最大化或最小化目标函数的线性规划、混合整数规划、二次规划、约束规划等问题。

Gurobi具有强大的求解能力和高效的算法，可以处理大规模复杂问题。它的求解器使用先进的优化技术，如线性规划的单纯形法、内点法以及整数规划的分支定界法和割平面法等。Gurobi还提供了丰富的API（应用程序编程接口），可以与各种编程语言（如Python、C++、Java等）进行集成，使开发者能够方便地使用它的功能来解决实际问题。
Gurobi的应用领域广泛，包括物流和运输优化、生产计划、资源分配、金融风险管理、电力系统调度等。通过使用Gurobi，用户可以对复杂的决策问题建立数学模型，并通过求解器获得最优或接近最优的解决方案，从而提高效率、降低成本或优化资源利用。

Gurobi的建模流程

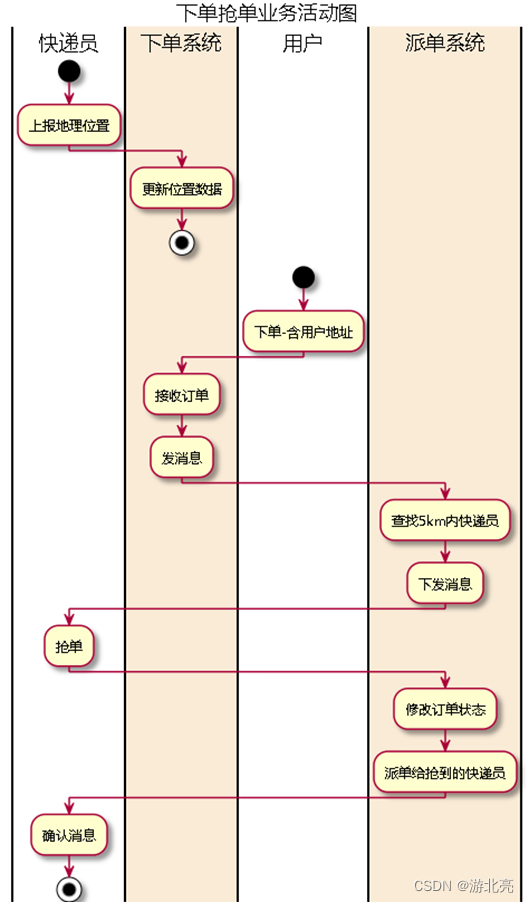
建模示例图

建模流程

定义变量；’(需要定义问题中所有的变量，并指定相应限制；如上下界限制和初始值等等；）
定义目标函数；(根据问题的要求设置目标函数，可以最大化或最小化某种目标)
定义约束条件；(根据问题的限制条件，设置相应的约束条件，例如等式约束、不等式约束等。需要注意的是，在设置约束条件时，需要保证所有的约束条件都被满足。)
执行优化函数；(调用内部优化函数来获取最终结果；)
检查求解状态并获取结果；获取相应的结果即可

注：1~4步骤对应的相关函数见流程图；下面示例也会有所体现

使用Gurobi解决优化问题示例1（需先在电脑上配置Gurobi环境）

预备知识

python基础语法；可参考(看到模块篇章就够用了)：廖雪峰python教程
Gurobi基础；可参考(Gurobi官网示例)：Gurobi

优化问题

实战数学优化问题1

题目示例图

示例1

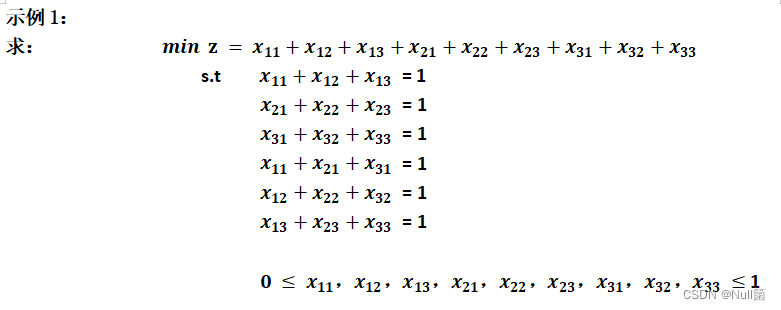
步骤解析（按照建模流程来）

基础步骤；导包

import gurobipy as gb
# 创建一个新的模型 调用内置函数Model()创建模型
model = gb.Model()

流程步骤；回顾

① 定义变量；定义问题中所有的变量，指定限制如上下界等，变量过多常用循环限制；
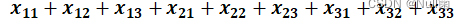
在这里插入图片描述

# 创建变量
x = {}
# 下标1~3；双循环将下标都表示出来
for i in range(1, 4):
    for j in range(1, 4):
        # 这一行代码的作用是，向数学优化模型中添加一个名为"xij"的新的二元变量x[i,j]，其取值范围为[0,1]。
        x[i, j] = model.addVar(lb=0, ub=1, name=f'x{i}{j}')

解释：model.addVar() 是一个用于向优化模型中添加变量的方法；并且可以指定这些变量的：名称、类型、上下界等特性；上述代码中传入了三个参数；lb=0代表变量下界为0，ub=1代表变量上界为1，name=f’x{i}{j}'代表变量的名称为x的索引i和j的字符串组合。

为了更好的理解上述代码，复习python字典（键值对）

x = {} # 创建了一个字典
x['key1'] = 'value1' # [ ] 的形式出来了
x['key2'] = 'value2'
print(x)  # 输出: {'key1': 'value1', 'key2': 'value2'}

但是我们想要x[i][j]的形式；这样我们就需要用到嵌套字典的知识，如下

x = {'a': {'kk': 1, 'why': 2}, 'b': {'hq': 3, 'qwe': 4}}

这样；我们可以使用 x[‘a’][‘kk’] 来访问 x 中第一个字典（即键为 ‘a’ 的字典）中键为 ‘kk’ 的值。这将返回值 1； x[i][j] 这样的语法，则假定 x 是一个嵌套字典，并且 i 和 j 是其键。因此，x[i][j] 表示获取嵌套字典 x 中键为 i 的值，然后再获取该值所对应的嵌套字典中键为 j 的值。
我们题解就是用到了嵌套字典的形式；上面项目就是生成一个个变量参数x[i][j]

② 定义目标函数；此处为最小化某种目标

# 设置目标函数
model.setObjective(sum(x[i, j] for i in range(1, 4) for j in range(1, 4)), gb.GRB.MINIMIZE)

解释：使用 gurobi 提供的 GRB.MINIMIZE 模式(固定写法)，表示我们要最小化目标函数。该目标函数是由两个嵌套的 for 循环所定义的，循环变量 i 和 j 分别遍历范围为 [1, 4) 的整数集合，因此这个目标函数的形式可以理解为

minimize: x[1, 1] + x[1, 2] + x[1, 3] + x[2, 1] + x[2, 2] + x[2, 3] + x[3, 1] + x[3, 2] + x[3, 3]

其中 x[i, j] 表示模型中的决策变量，它们的值可以是任意实数，并且在其他约束条件下可能会被限制。通过最小化这个目标函数，我们希望找到一组值使得所有决策变量的总和尽可能地小。

③ 定义约束条件；将s.t.中的约束条件表示出来即可；

for i in range(1, 4):
    model.addConstr(sum(x[i, j] for j in range(1, 4)) == 1, name=f'c{i}')

for j in range(1, 4):
    model.addConstr(sum(x[i, j] for i in range(1, 4)) == 1, name=f'c{j+3}')

解释： model.addConstr() 用于添加约束条件；① sum(x[i, j] for j in range(1, 4)) == 1；表示在所有列（j）上，第 i 行上的决策变量 x[i, j] 的总和必须等于 1。也就是说，每一行上只能选择一个 x[i, j] 变量为 1，其他都必须为 0；
其中还有一个约束条件：在① 定义变量的时候已经解决了【范围】；
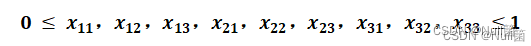
在这里插入图片描述
④ 执行优化函数；固定写法

# 执行优化函数
model.optimize()

⑤ 检查求解状态并获取结果；最后获取相应的结果即可

# 检查求解状态
if model.status == gb.GRB.OPTIMAL:
# 打印最优解
    print('最优解是:')
    for i in range(1, 4):
        for j in range(1, 4):
            print(f'x{i}{j}: {x[i, j].x}')
    print('目标函数值:', model.objVal)
else:
    print('未找到最优解。')

实战数学优化问题1完整代码

# 基础步骤
import gurobipy as gb
model = gb.Model()

# 流程步骤
# ① 定义变量
x = {}
for i in range(1, 4):
    for j in range(1, 4):
        x[i, j] = model.addVar(lb=0, ub=1, name=f'x{i}{j}')

# ② 定义目标函数
model.setObjective(sum(x[i, j] for i in range(1, 4) for j in range(1, 4)), gb.GRB.MINIMIZE)

# ③ 定义约束条件
for i in range(1, 4):
    model.addConstr(sum(x[i, j] for j in range(1, 4)) == 1, name=f'c{i}')

for j in range(1, 4):
    model.addConstr(sum(x[i, j] for i in range(1, 4)) == 1, name=f'c{j+3}')
    
# ④ 执行优化函数
model.optimize()

# ⑤ 检查求解状态并获取结果
if model.status == gb.GRB.OPTIMAL:
    # 打印最优解
    print('最优解是:')
    for i in range(1, 4):
        for j in range(1, 4):
            print(f'x{i}{j}: {x[i, j].x}')
    print('目标函数值是:', model.objVal)
else:
    print('未找到最优解。')