0.前言

1.算法的复杂度简述

2.时间复杂度

2.1 什么是时间复杂度

2.2 大O表示法

2.2.1 例一

2.2.2 大O表示法规则

2.2.3 例二

2.2.4 例三

2.2.5 例四

2.2.6 例五

2.2.7 例六

2.2.8 例七

2.3 时间复杂度计算总结

3.空间复杂度

3.1 空间复杂度的量度

3.2 例一

3.3 例二

3.4 例三

3.5 例四

4.复杂度OJ（带你在实战中分析复杂度）

4.1 P1 消失的数字

4.1.1解法一

4.1.2解法二

4.1.3解法三

4.1.4解法四

4.2 P2 左旋转字符串

4.2.1 暴力挪动法

4.2.2 空间换时间

4.2.3 三旋转法

0.前言

本篇博客所有代码以及思维导图都已上传至Gitee，可自取：

1时间空间复杂度 · onlookerzy123456qwq/data_structure_practice_primer - 码云 - 开源中国 (gitee.com)https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/1%E6%97%B6%E9%97%B4%E7%A9%BA%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6

1.算法的复杂度简述

算法，是针对一个具体问题，我使用的某一个特定方法，而每种解决方法都要耗费时间资源和空间(内存)资源。衡量一个算法的好坏，我们通常是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

PS：由摩尔定律可知，我们的内存空间越来越有盈余，内存成本逐渐下降，而运行速度即CPU的算力其实遇到了瓶颈，所以我们在当代更加关注时间性能的提升。

2.时间复杂度

2.1 什么是时间复杂度

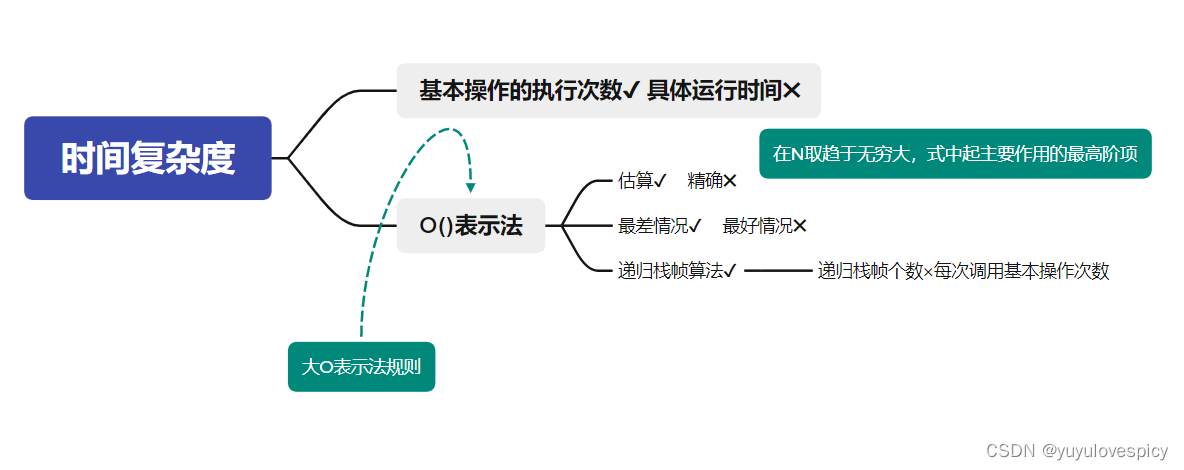
首先我们要确定一件事情，时间复杂度并不是算这种算法，全过程具体用了多少秒。因为在不同的环境下，计算的具体秒数是不同的。比如你在一个二十年前的电脑上跑，和在一个搭载3090的拯救者上跑，其计算秒数一定是不同的。我们无法掌控具体的运算时间。

时间复杂度的量度，是基本操作的执行次数。在同一段代码中，其基本操作的个数是可以具体量化的。例如我们这个算法要解决这个问题，需要做1000次基本操作，你这个算法要做1000*1000次基本操作才能跑出来，而不是各个算法具体要多少秒跑出来。

void Func1(int N)
{
    int count = 0;
    //第一个for循环
    for (int i = 0; i < N ; ++ i)
    {
         for (int j = 0; j < N ; ++ j)
         {
             ++count;
         }
    }
    //第二个for循环
    for (int k = 0; k < 2 * N ; ++ k)
    {
     ++count;
    }
    //while循环
    int M = 10;
    while (M--)
    {
     ++count;
    }

    printf("%d\n", count);
}

例如如上代码，要计算时间复杂度，我们就要求出执行基本操作的次数，第一个for循环基本操作的次数就是N次，第二个for循环中，基本操作的次数是2*N，还有while循环基本操作的次数是10次。所以Func1基本操作的总数是3*N+10次。

时间复杂度并不是用精确的基本操作次数3*N+10来表示，事实上，时间复杂度使用的大O表示法，来粗略的表示基本操作次数，下面我们看大O表示法如何化简表示基本操作次数。

2.2 大O表示法

2.2.1 例一

我们举一个例子，比如一个算法的基本操作次数为 $F(N) = 2*N^{2} + 2*N + 10$

N=10	F(10)	230
N=100	F(100)	20210
N=1000	F(1000)	2002010
N=10000	F(10000)	200020010

我们看到随着N的逐渐增加，影响基本操作次数的主导因素到了 $2*N^{2}$ 上，其他的一次项和常数项并不能左右整体的大小。大O表示法，其实就是只要影响力最大的那一项。也就是说在N -> 无穷，越来越大时，只保留最影响主体最大的那一项。

所以我们提取出 $2*N^{2}$ 这一项，然后大O表示法还需要去掉系数，只需要去单位大小即可，如 $2*N^{2}$ 写成 $N^{2}$ ，0.5*N写成N。

所以 $F(N) = 2*N^{2} + 2*N + 10$ 某个算法的具体操作次数，用大O表示法，得出该算法的时间复杂度为 $O(N^{2})$ 。

2.2.2 大O表示法规则

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

4、在实际中一般情况关注的是算法的最坏运行情况。

我们在接下来的代码实践当中进行规则应用，学习时间复杂度的计算方法。

2.2.3 例二

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
 int count = 0;
 for (int k = 0; k < M; ++ k)
 {
 ++count;
 }
 for (int k = 0; k < N ; ++ k)
 {
 ++count;
 }
 printf("%d\n", count);
}

在这个例子当中，我们可以算出基本操作的次数，为M+N，而我们知道计算时间复杂度，取的是当数趋于无穷大时，在次数大小起主导作用的项。而M和N我们并不知道谁更占主体。所以此时需要分情况讨论。

情况一：如果M远大于N，那时间复杂度为O（M）；

情况一：如果N远大于M，那时间复杂度为O（N）；

情况一：如果M和N相当，差不多大，那时间复杂度为O（M）或 O（N）都可以；

2.2.4 例三

// 计算Func4的时间复杂度？
void Func4(int N)
{
 int count = 0;
 for (int k = 0; k < 100; ++ k)
 {
 ++count;
 }
 printf("%d\n", count);
}

Func4基本操作的次数是100，而根据大O表示法的规则，Func4的时间复杂度就是O（1），这里的1并不是指1次，而值得是常数次。

2.2.5 例四

const char * strchr ( const char * str, int character )
{
    int i = 0;
    while(str[i] != '\0')
    {
        if(str[i]==character)
        {    
            return str+i;
        }
    }
    return NULL;
}

在一个字符串str当中，寻找character这个字符，我们就需要遍历这个字符串，查看有无这个字符。可是有可能这个字符一下子就能找到，也有可能遍历到最后才能找到，情况是多样的。

许多算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数 ( 上界 )

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数 ( 下界 )

如我们刚才的搜索字符串中特定字符，最坏情况下基本搜寻操作的次数是N，平均次数是N/2，最好情况是1常数次。

在时间复杂度计算中，我们是关注的是算法的最坏运行情况，所以字符串中搜索字符的时间复杂度为O(N)

2.2.6 例五

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
 if (a[i-1] > a[i])
 {
 Swap(&a[i-1], &a[i]);
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

冒泡排序所需要做的基本操作次数，最坏的情况下是0+1+2+...+N-1= $\frac{N(N-1)}{2}$ 次，也即 $\frac{1}{2}N^{2}-\frac{1}{2}N$ ，而最好情况下（也就是一开始就是顺序的情况下），我们要做的基本操作次数只需要 $N$ 次。

时间复杂度是一个悲观的预期。最好平均 最坏✔

所以冒泡排序时间复杂度为 $\frac{1}{2}N^{2}-\frac{1}{2}N$ -> $N^{2}$ ，即 $O(N^{2})$ 。

2.2.7 例六

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
 assert(a);
 int begin = 0;
 int end = n-1;
 while (begin < end)
 {
 int mid = begin + ((end-begin)>>1);
 if (a[mid] < x)
 begin = mid+1;
 else if (a[mid] > x)
 end = mid;
 else
 return mid;
 }
 return -1;
}

再看一个二分查找算法。

时间复杂度看的基本操作的次数，不能简单的，而是要深入过程，深入思想，看其所作基本操作的次数。

首先我们回忆一下二分查找算法的基本查找逻辑：

二分查找就是对一个顺序（我们以从小到大为例）的数组，每次对比剩下区域的中间大小的数，如果比中间数大则继续操作上半段数，比中间数小则继续操作下半段数，相等则意味着找到了，就结束查找。这样我们就可以看到每次都在砍掉数组的一半长度，直到把数组砍到只剩下最后一个元素，才为查找完毕。

而时间复杂度算的是最悲观的情况，所以我们取的是最悲观的情况，也就是每次砍掉一半，砍到最后只剩一个元素。

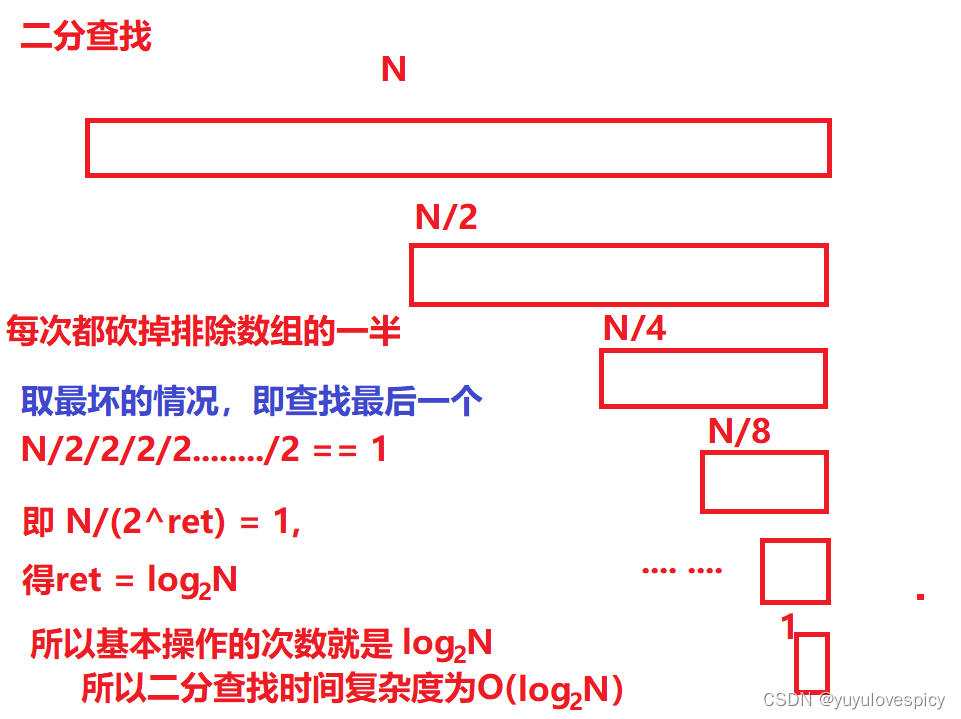
然后我们以二分查找（其实是log2N时间复杂度的任何算法）为例，看一下二分查找这个算法在效率上的优秀。

所以我们看到，在10亿中查一个人，我们仅需要查找30次。而在20亿中查，我们也仅需要查30+1==31次。这查找效率堪称优秀！

2.2.8 例七

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
 if(0 == N)
 return 1;
 
 return Fac(N-1)*N;
}

递归的时间复杂度算法：需要看栈帧展开图

算法其实就是 递归的次数(展开过的栈帧的个数) 乘以每次函数调用的基本操作次数。也即递归次数*每次递归调用的次数。

2.2.9 例八

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

画递归的栈帧展开图，求出递归次数。然后我们可以看出每次递归调用的基本操作次数都是1。两者相乘。

所以事实上，斐波那契数列的递归写法其实就是一个实际没用的算法，因为太慢了。

现在我们来建立一个观念，O（2^N）的时间复杂度实际上是非常非常非常慢的。n取30，仅仅求一个Fib(30)，我们要做的基本操作次数就要跑10亿次！而n取40，仅仅求一个Fib(40)，我们要做的基本操作次数居然达到了壹万亿次！会产生指数爆炸的现象。

所以我们求斐波那契数列实际上用循环迭代法，而不用递归算法。

2.3 时间复杂度计算总结

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

4、在实际中一般情况关注的是算法的最坏运行情况。

5、递归的时间复杂度算法：递归次数×每次递归调用的次数。

3.空间复杂度

3.1 空间复杂度的量度

空间复杂度，是 临时额外最大所占用存储空间大小的量度。

空间复杂度并不是具体精确到，一个算法，即你要解决这个问题，要耗费具体多少个字节。空间复杂度求法的基本量度应该是所用变量的个数。同时我们要注意，这个变量个数有桑耳限定词，临时额外最大的所用变量个数。

同时我们表示空间复杂度，也是采用大O表示法，来粗略的表示所用变量的个数。

我们在具体的实例中理解空间复杂度的求法。

3.2 例一

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
 if (a[i-1] > a[i])
 {
 Swap(&a[i-1], &a[i]);
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

计算冒泡排序的空间复杂度。

下面我们进行变量个数的统计（临时额外最大的所用变量个数）。我们看到次程序当中有n个变量的数组a，也有我们定义的变量end，i，exchange。但是我们计算空间复杂度，看的是额外定义的变量个数，看的是为了解决这个问题而新额外定义的变量。所以int* a数组的n个变量不参与统计。

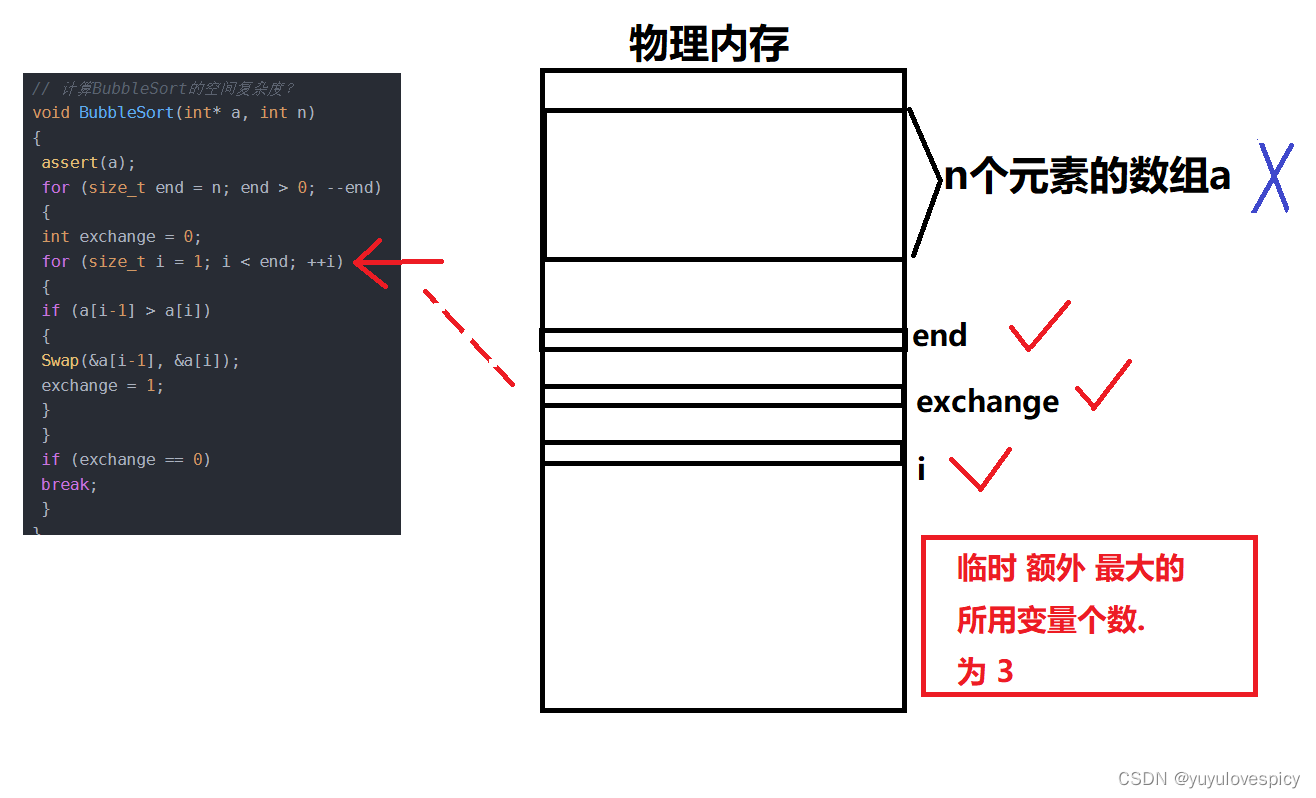
然后我们理解临时最大的变量个数，计算的是所有时刻当中，所占用的空间的最大值，也就看的是在所有时刻中，选出变量的个数最多的那个时刻。

比如说我们这个冒泡排序的例子中，是在进入最内层的那个for循环当中，我们临时使用的变量个数到达最大（end + exchange + i）3个。

再根据大O表示法进行化简，我们得到冒泡排序的空间复杂度为O（1）。【3->O（3）->O（1）】

3.3 例二

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
 if(n==0)
 return NULL;
 
 long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
 fibArray[0] = 0;
 fibArray[1] = 1;
 for (int i = 2; i <= n ; ++i)
 {
 fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 }
 return fibArray;
}

我们看到Fibonacci函数中，在堆区开辟了（n+1）个变量，还有在栈区开辟了1个指针变量，此外就再无定义的变量个数了

3.4 例三

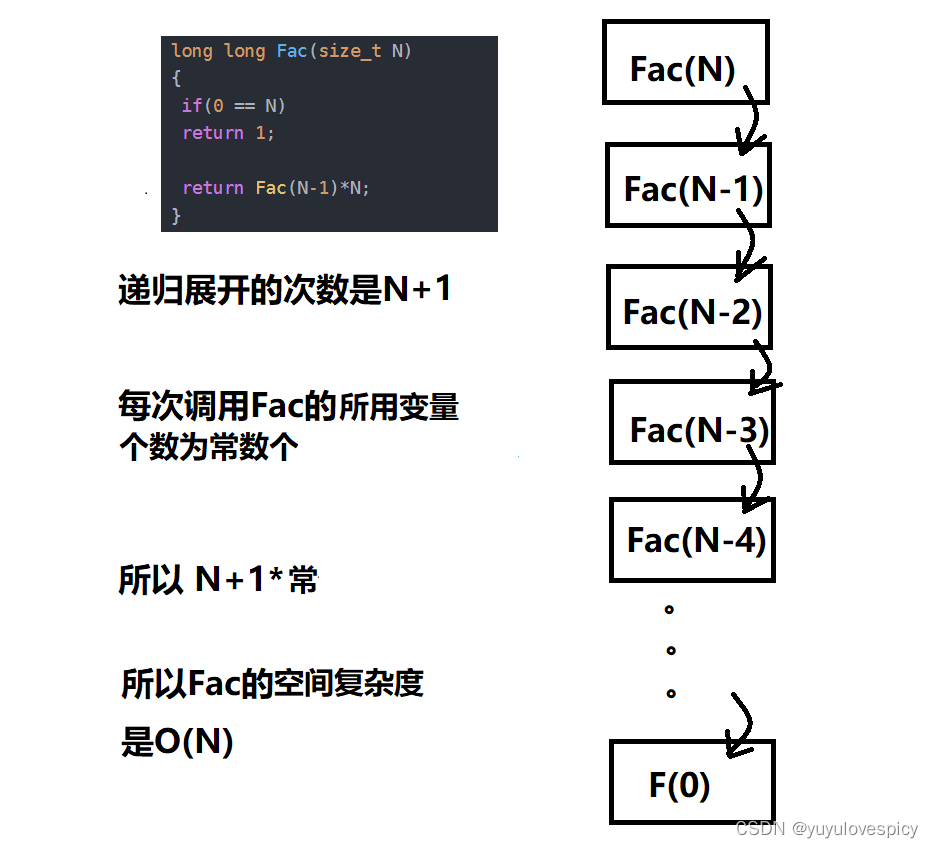
// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}

对于 递归调用函数算法的空间复杂度，其计算方法是 展开栈帧的次数*每个栈帧最大所用的变量个数。

开辟了N+1个栈帧，每个栈帧使用了常数个空间，所以额外最大临时定义的变量数就是（N+1）* 常数。所以O（（N+1）* 常数）， 空间复杂度为O（N）。

3.5 例四

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

递归函数算法的空间复杂度算法，并不是像时间复杂度一样，需要你算出所有的展开的总个数再乘以每个栈帧的总变量个数，我们首先要知道一件事：时间是不断累积的，而空间是可以重复利用的。我们举一个生动的例子进行说明：

例如我们有一个缸和在仓库中很多的桶，但是每一个桶都有一个特性，用一次就会化成空气，用完就得去仓库里拿新的一个。我们需要用一趟一趟的用水桶把水缸填满，这时候我们一桶一桶把水缸的盛满的过程中，其实我们会用坏很多的桶，空间复杂度是看所有时刻中使用变量个数的最大的时刻，并不一定是全过程你使用过的所有变量个数的累计，而你即使用过那么多的桶，假设我们用过1000个桶，而在所有时刻内，我们最多所用到的总空间其实就是只有一个水桶（之前的水桶都化成空气了，并没有占我空间），所以只能说此时的空间复杂度只能是一个水桶。

对于递归调用函数算法的空间复杂度，其计算方法更准确的说是 曾展开过的栈帧的最大次数*每个栈帧最大所用的变量个数。（PS：这个 曾展开过的栈帧的最大次数，说明白一点，就

是函数递归，栈帧所到达的最大深度）

下图是Fib展开过的所有栈帧数量的累计：

下面我看这个过程中Fib算法的栈帧展开过程：[注意看最大递归深度]

我们看整个变化的过程当中：栈帧展开的最大深度（函数栈帧所占栈区的最大空间）为N-1，而每一次展开的栈帧中，我们所使用到的变量个数都是1。(N-1)*1 = N-1，所以用大O表示法，我们知道Fib的空间复杂度是O(N)。

4.复杂度OJ（带你在实战中分析复杂度）

下面我们做几个力扣OJ的题，来具体应用刚刚学到的时间复杂度和空间复杂度的分析。

4.1 P1 消失的数字

下面是原题，在numsSize个数的数组nums当中，存储着0----n其中的n-1个数，我们现在需要找到是缺了哪一个数。

4.1.1解法一

可以对nums数组进行升序排序，然后对这个排序之后的数组进行遍历，当数组下标不等于改下标nums数组上的数据时，我们就找到了这个缺失的数。

int cmp(const void* e1,const void* e2)
{
    return *((int*)e1) - *((int*)e2);
}
int missingNumber(int* nums, int numsSize){
    //C语言快排&&cmp升序排列
    qsort(nums,numsSize,sizeof(int),cmp);
    for(int i=0;i<numsSize;++i)
    {
        if(nums[i]!=i){
            return i;
        }
    }
    return numsSize; 
}

我们使用的是C语言中的qsort接口进行排序，其底层逻辑是quick sort快排，快排的时间复杂度是 $O(N*log{_{2}}^{N})$ ，然后遍历一遍nums的所需最坏也是 $O(N)$ ，所以该种方法的时间复杂度就是 $O(N*log{_{2}}^{N})$ + $O(N)$ = $O(N*log{_{2}}^{N})$ 。同时这个方法当中，我们只定义了常数个变量，所以空间复杂度是 $O(1)$ 。

4.1.2解法二

我们让(0+1+2+3+......+n)减去(nums[0]+nums[1]+nums[2]+nums[3]+......nums[n-1])，最后的结果就是缺少消失的数字。

int missingNumber(int* nums, int numsSize){
    //numsSize是nums的元素数目大小n
    //(0+1+2+3+......+n)
    //减去(nums[0]+nums[1]+nums[2]+nums[3]+......nums[n-1])
    long long sum = 0;
    for(int i=0;i<numsSize;++i)
    {
        sum+=i;
        sum-=nums[i];
    }
    sum+=numsSize;
    return sum;
}

这样我们看到整体方法当中，额外所使用的变量个数为常数个，所以空间复杂度是O(1)。

而整体只是遍历了数组一遍，基本操作的次数是N，所以时间复杂度是O(N)。

4.1.3解法三

新开辟一块n+1大小的数组，下标从0到n，哪一个位置有值，我们就在哪个下标的位置上填入值。最后遍历查看，哪个下标没有被赋值，哪个下标就是缺少的数字。

int missingNumber(int* nums, int numsSize){
    //开辟一段n+1的数组
    int* ptmp = (int*)malloc(sizeof(int)*(numsSize+1));
    //设置初始值为0
    memset(ptmp,0,sizeof(int)*(numsSize+1));
    //然后根据nums对每个位置赋值
    for(int i=0;i<numsSize;++i)
    {
        //若出现则下标处赋值为1
        ptmp[nums[i]] = 1; 
    }
    for(int i=0;i<numsSize+1;++i)
    {
        if(ptmp[i]==0)
            return i;
    }
    return -1;
}

我们额外开辟使用了（n+1）个变量的数组，所以空间复杂度就是O(N)。

过程当中我们对数组中每一个元素赋值为0，然后赋值1，最后检查，遍历了三次数组。总体的基本操作次数有3N，所以本算法的时间复杂度就是O（N）。

4.1.4解法四

利用异或的特性，示例就是a^b^b^c^c == a，我们让0去异或0，1，2，3......n，以及异或nums[0]，nums[1]，nums[2]......nums[n-1]，在两个序列当中都存在的数异或后就都没了，最后得出的结果就是那个缺少的数字。

int missingNumber(int* nums, int numsSize) {
    int ret = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        ret ^= nums[i];
        ret ^= i;
    }
    ret ^= numsSize;
    return ret;
}

我们只使用了两个额外的变量，所以空间复杂度就是O（1）。

然后全过程的基本操作我们只是遍历了一次，所以时间复杂度就是O（N）。

4.2 P2 左旋转字符串

4.2.1 暴力挪动法

实现整体的挪动，就把每一个字符都往前挪，一共挪动k次。

char* reverseLeftWords(char* s, int n){
    //把字符串s往左旋n位
    char* start = s;
    int len = strlen(s);
    while(n--)
    {
        char tmp = s[0];    
        int i = 0;
        s=start;
        while(i<len-1)
        {
            //进行往下一个元素的覆盖
            s[i] = s[i+1];
            i++;
        }
        s[len-1]=tmp;
    }
    return start; 
}

分析这个方法，对于这个N个元素的字符串，我们总共挪动了n次，每次挪动都会做N次基本操作。所以该方法的基本操作次数是n*N，当n的大小和N差不多大时，该种方法是较坏的情况，时间复杂度是一种悲观的预期，故时间复杂度是O（N^2）。

在本算法当中我们只是定义了常数个变量，所以空间复杂度是O（1）。

4.2.2 空间换时间

另外开辟n个空间的大小，存储s[0]----s[n-1]的数据，然后让后面的字符都依次从s[0]开始往后填入，最后再填入我们的存储的n个首元素即可。

char* reverseLeftWords(char* s, int n){
   char* ptmp = (char*)malloc(sizeof(char)*n);
   for(int i=0;i<n;++i)
   {
       ptmp[i]=s[i];
   }
   int index = 0;
   int i = n;
   while(s[i]!='\0')
   {
       s[index++]=s[i++];
   }
   i = 0;
   while(n--)
   {
       s[index++]=ptmp[i++];
   }
   return s;
}

这种方法下，我们新开辟使用了(n+1)个变量，当n逼近于N时，是悲观的情况，所以空间复杂度就是O（N）。

本次方法我们遍历了两个字符串的长度，基本操作的个数是2*N，所以时间复杂度就是O(N)。

4.2.3 三旋转法

最后这个算法，是一个非常神奇且高效的算法，堪称是本题的最优解了。

我们首先对[0]----[n-1]这n个字符 && [n]----[strlen-1]这strlen-n个字符，分别进行reverse倒置，然后对整体字符串[0]----[strlen-1]进行reverse倒置，之后得到的结果就是左旋之后的结果。

如我们看“abcdef”，n==2时，"abcdef"=>"bafedc"=>"cdefab"。

void reversestring(char* s,int left,int right)
{
    //旋转字符串s，从[left,right]区域的字符串
    while(right>=left)
    {
        char tmp = s[left];
        s[left] = s[right];
        s[right] = tmp;
        ++left;--right;         
    }
}
char* reverseLeftWords(char* s, int n){
    int len = strlen(s);
    reversestring(s,0,n-1);
    reversestring(s,n,len-1);

    reversestring(s,0,len-1);
    return s;
}