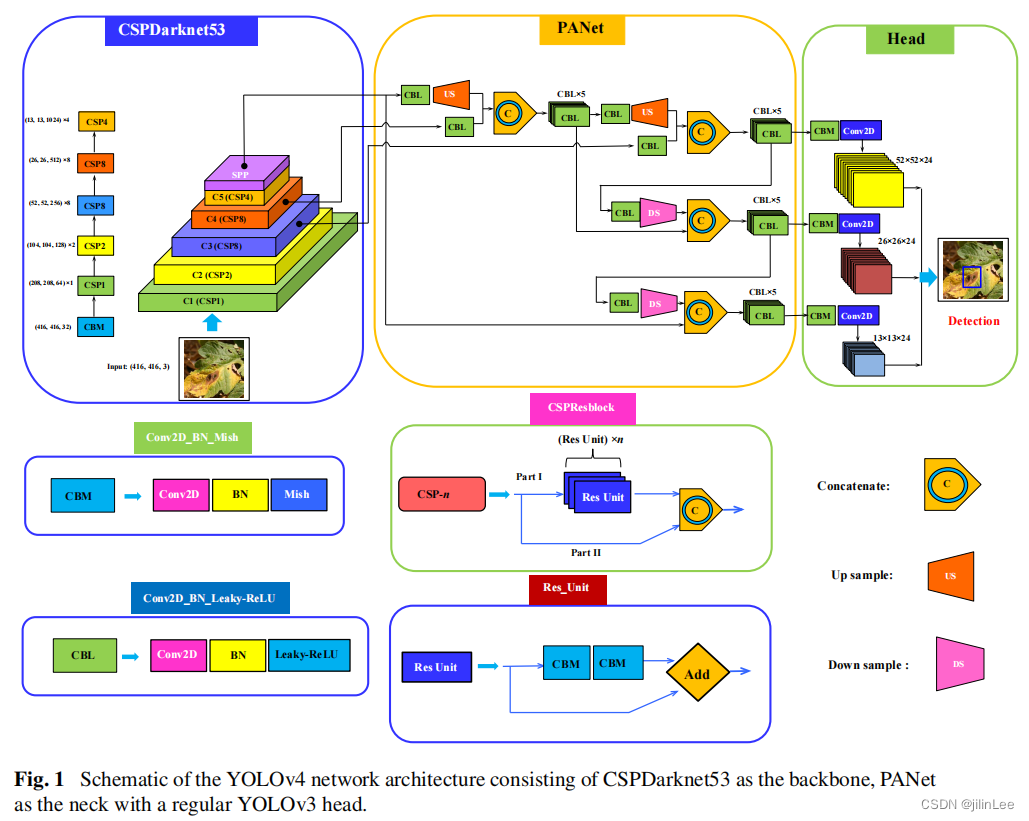
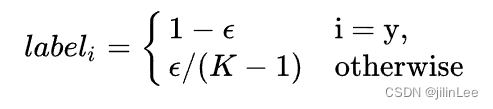感觉V3 到V4，YOLO的整体架构并没有重大的改进，只是增加了很多的trick

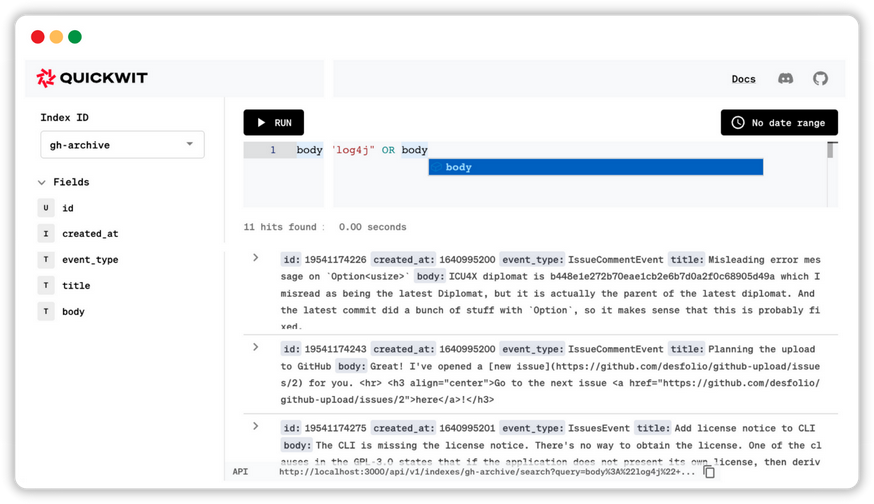
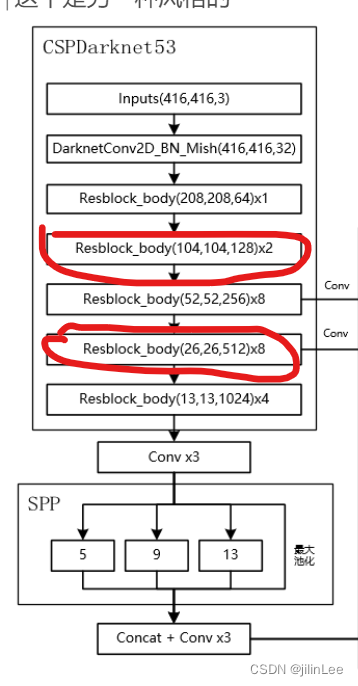
先展示一下V4的整体网络结构

$\uparrow$这个是对比V3的

如图可见，V4的结构依然是主干网络+金字塔+头部检测器，所有的改进都是为了更好更快的检测目标。

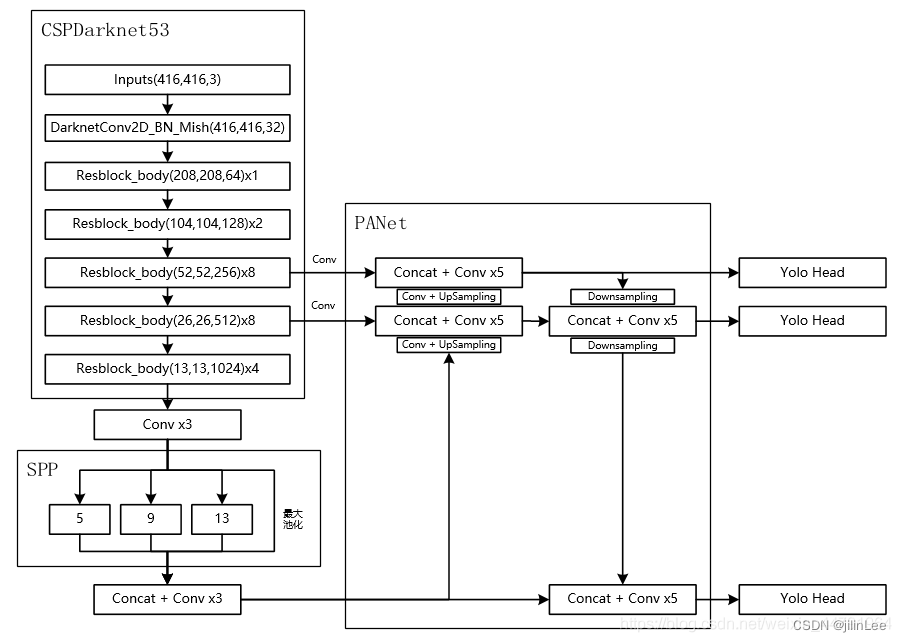
$\uparrow$这个是另一种风格的

$\uparrow$这个卷积块的角度看

然后，是V4的改进：

• 主干网络：DarkNet-53 改为CSPDarkNet-53
• 激活函数：LeakyReLU改为Mish
• 金字塔：FPN改为PAN
• SPP
• DropBlock正则化
• 数据增强：CutMix、马赛克（Mosaic）、
• 自对抗训练
• 标签平滑
• 学习率：余弦退火衰减
• 损失函数：IoU 改为 CIoU

首先，V5在训练之前加入了mosaic数据增强方法，提高小目标的检测性能，放上美女图。。。

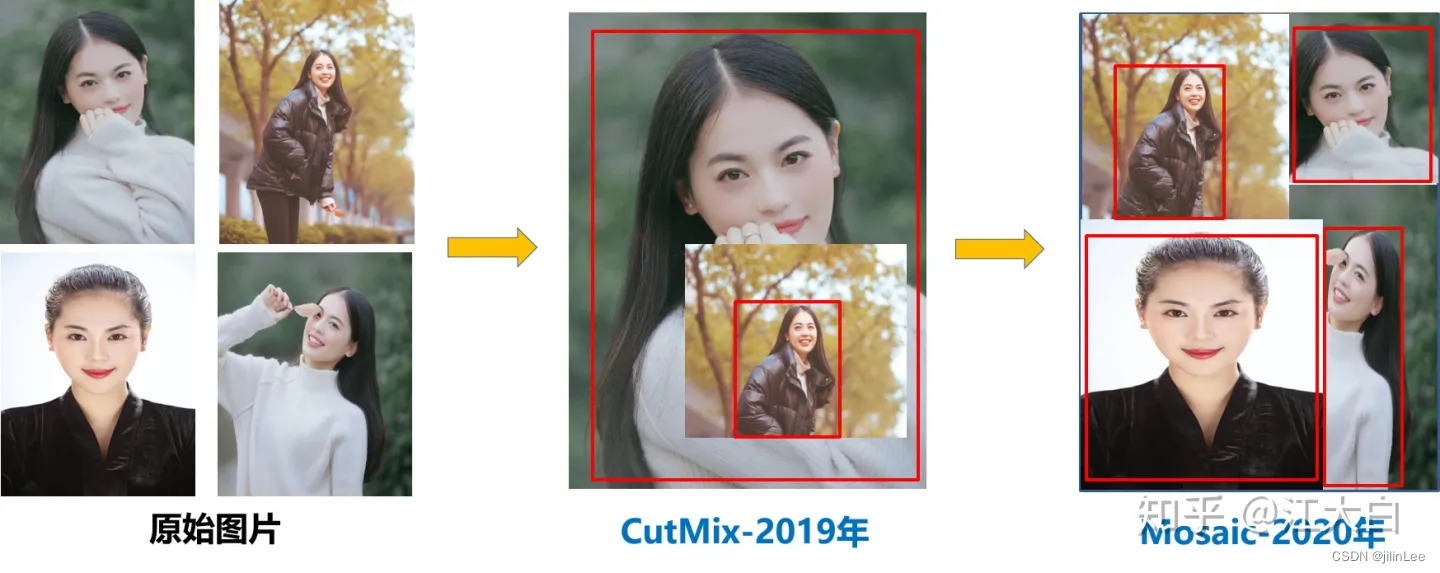
mosaic数据增强方法仅仅是使用，并没有在进一步优化。这种方法在BN层计算特征的时候，会同时计算四张图片的数据，极大丰富了检测物体的背景。

1）CSPDarkNet作为主干网络，相比于DarkNet，虽然增加了大量卷积模块，但网络的推算算法却没有降低。首先，CSP全称Cross Stage Partial Network，翻译过来是跨阶段部分网络，意味着这种网络结构中存在一种可以跨越很多层传递特征的结构。

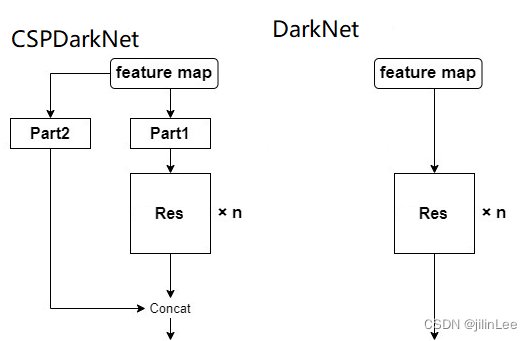
如上图所示，这里的Res指带的不是单个的残差块，而是YOLO中的堆叠残差结构

这种结构，会有大量的卷积运算，并且为了更好的提高模型对图像特征的提取能力，CSPDarknet-53还参考了DenseNet的密集链接，进一步加大了计算量也提高了性能。于是，为了提高速度，通过CSP结构，这种将Feature作为大残差边的方式，将输入Feature的拆成两份，一部分直接跨层传递，极大的减少了计算量。

这么做的合理性在于卷积网络中的feature map往往具有很大的冗余性，不同通道的特征图可能包含的信息是相似的。因此，无需处理全部的channel，只需处理一部分即可。

2）Mish激活函数
YOLOv4还将LeakyReLU全部换成了Mish

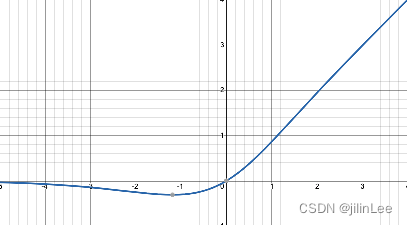
Mish是一种平滑的，非单调的激活函数，可以定义为：

Mish(x) = x・tanh(softmax(x)) ；其中softmax= ln(1 + e ^ x)

相比于LeakyReLU，Mish在（-oo,0）这个区间可以更好的保持较小的负值，使大多数深层神经元能得到有效更新，不过这个函数的计算时间要高于LeakyReLU，但是在性能上表现出了比他们都要好的效果，应用在CSPDarknet中确实提升了大幅性能，并且感谢CSP的跨层结构，Mish函数对整体的计算量负担不大。

3）SPP池化
SPP池化主要作用在于不增加下采样数量的条件下，扩大YOLO检测器的感受野。比如，一张512X512的图像，原始V3中13X13特征图对应的感受野为512x512，而加入了SPP后提高到725x725。它借鉴了SPPnet的结构，但也不是完全相同.具体结构如下图

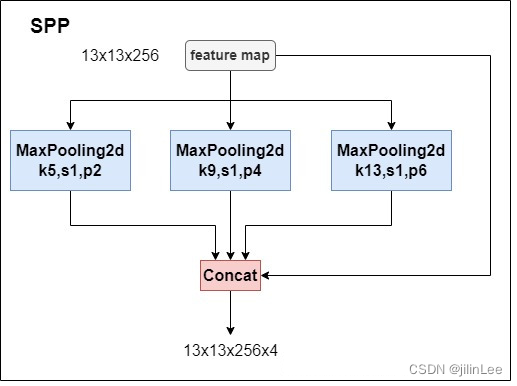
这个结构由何凯明提出，用于物体的多分类任务。由于COCO数据集中，输入图像的尺寸总是改变，而分类网络，在网络最后一定有全连接层，这就需要所有图像转换到相同的尺寸。但这会扭曲原始的图像中的物体，因此为了很好的解决这样的问题， SPPNet使得任意大小的特征图都能够转换成固定大小的特征向量，送入全连接层。

但这个思路是针对于分类任务的，对于进行目标检测任务的YOLO v4而言，不需要在SPP这里设定全连接层进行分类，而是选取了SPP中，池化（下采样）部分来提取不同感受野的特征。

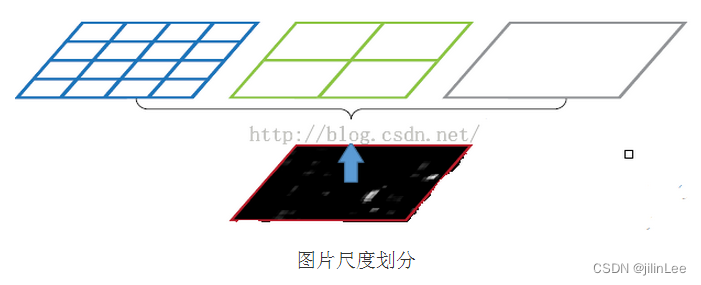
如图，通过3个并行池化模块，分别对特征图按照不同步长进行计算。这样，网络可以增大感受野，使模型更改好的检测大目标和小目标。

4）PANet
YOLOv4的第二处改进便是参考了PANet（Path Aggregation Network）论文的结构。原先的YOLOv3仅使用了top-down结构的FPN，而PAN是在此基础上加了bottom-up的结构。

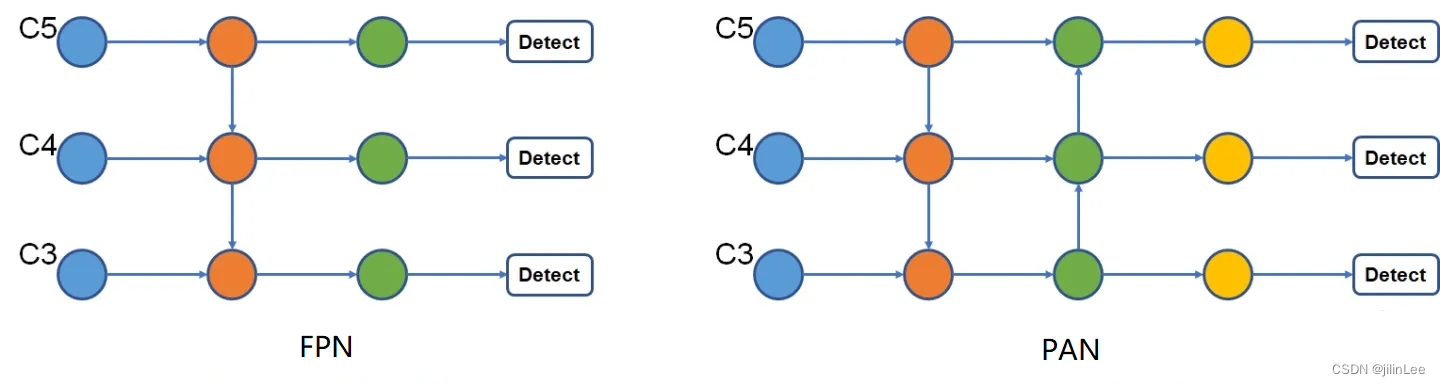
假设输入图像为416X416像素,则C5是末端13X13的特征图，C4是26X26的，C3是52X52的特征图。可见，第一步，通过将特征上下融合，使得C3和C4特征图包含了更多的深层语义信息；第二步，再次下上融合，使得C5和C4特征图包含了更多的浅层纹理信息，提升了网络的检测性能。

5） 损失函数
Loss这里改动有3个，一个是定位，微调了中心点（x,y）的回归公式，另一个是置信度的判定由IoU改进为CIoU，再有一个就是Multi anchor策略

1））

在YOLOv3中，边界框的中心点回归公式如下：

$c_x=gri{d}_x+\sigma (t_x)$
$c_y=gri{d}_y+\sigma (t_y)$

简洁明了，但是这里存在一个隐患，那就是当物体的中心点恰好落在网格的右边界时，那么就需要$\sigma (t_x)$输出为1。
但对于sigmoid函数，当且仅当输入为正无穷的时候，输出才是1，但显然让网络学一个这种正无穷是不现实的。同样，当物体中的中心恰好落在网格的左边界时，就需要 $\sigma (t_x)$输出为0，而sigmoid函数只有输入负无穷时，才会得到0的输出，这显然也是不合适的。这一问题就被称为“grid sensitive”，问题的核心就在于目标的中心点可能会落在网格的边界上。

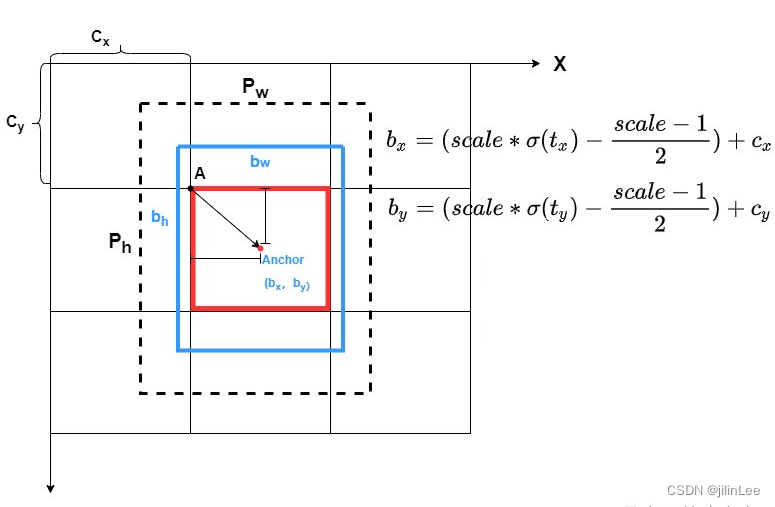
为了解决这一问题，YOLOv4便在$\sigma (t_x)$函数前面乘以一个大于1的系数：

当中心点处在右边界的时候，$s\ast \sigma (t_x)$输出为1，那么仅需$\sigma (t_x)$输出为$1/s<1$，从而避免正无穷的问题。但是，这种做法并不会解决$s\ast \sigma (t_x)$输出0的问题，仍旧有负无穷的问题存在。于是，增加了常数项$(s-1)/2$解决了中心点落到左边界的问题。

$c_x=gri{d}_x+(s\ast \sigma (t_x)+(s-1)/2)$
$c_y=gri{d}_y+(s\ast \sigma (t_y)+(s-1)/2)$

2））CIoU

IOU Loss：考虑检测框和目标框重叠面积。
GIOU Loss：在IOU的基础上，解决边界框不重合时的问题。
DIOU Loss：在IOU的基础上，考虑边界框中心距离的信息。
CIOU Loss：在DIOU的基础上，考虑边界框宽高比的尺度信息。

因此，CIoU可以说考虑到了各种情况，嗯。。。很完美，可以说V4，使用CIoU提高了网络对于正样本的学习数量，并优化了对小目标的检测能力。

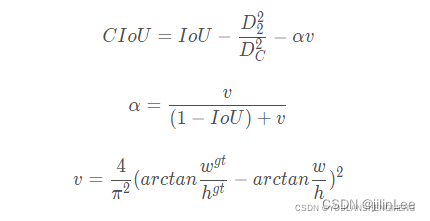
注意一点
V4的损失函数中，$Los{s}_{loc}$的计算方式不同于V3直接使用xywh计算，而是使用了CIoU来计算，也就是说需要通过xywh反算出整个包围框之后在于真实的标签框计算CIoU，然后带入$Los{s}_{loc}$

3））Multi anchor策略
V3中正样本的判定机制是：当预测中心点与存在真正有物体中心点，处于同一网格中时，进行IoU的计算，并且当IoU>0.7时的最大的那个（三个检测器同时算的，每个网络2个框，共6个，是6选1）才算正样本，并为了更进一步提高正样本的权重，V3通过加入系数${\lambda }_{coord}$，这种固定的方式强行提高，比如当网格中有真实物体，这里的${\lambda }_{coord}=5.0$，负样本的${\lambda }_{coord}=0.5$。

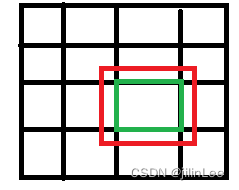
这种匹配机制导致正样本过少，产生正负样本不均匀的问题。毕竟网格比较少，尤其是小目标的情况。于是，V4将单个网格的范围从[0,1]图上绿色框阔大到了[-0.5,1.5]红色框，这样即便预测框的中心点处于另一个网格中，也会计算IoU，提高了正样本的数量，并且设定一个阈值，只要预测框的iou大于这个阈值则判定为正样本（三个检测器同时算每个网络2个框，共6个，有可能6个全要）。

6）标签平滑
为了防止分类过拟合，使用了标签平滑Label Smoothing的技巧。

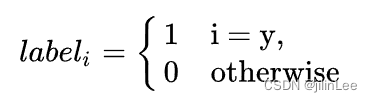
在分类任务中，某个样本的one-hot（二进制串）标签为

[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0]

二分类，认为样本为正样本，标注为1，过于绝对，容易过拟合；好比一个人，过于自信，就是自负，一旦自负，迟早判断失误！将上述的(0, 1)定义为(0.05, 0.95)，这样标签变得平滑，有种将离散变量转为连续变量的意思，类似于“像素插值”。

在训练过程中，模型习惯于对其预测结果“过于自信”，这会增加过拟合风险。另外，数据集中可能包含标注错误的数据，所以模型在训练过程中需要对标签持有怀疑态度。为此，可以在训练中引入一种标签平滑方法，将hard标签转换为soft标签（即1 → 1 - 平滑因子），来降低模型对标签的信心。