什么是语言模型?
一个传统的语言生成模型可以用于识别或生成字符串
我们可以将有穷自动机看作是一种确定性的语言模型

基本模型:每一个文档都是通过一个像这样的自动机生成的,只不过这种自动机是有概率的
一种最简单的语言模型等价于一个概率有穷自动机,该自动机仅仅由一个节点组成,它也只有一个生成不同词项的概率分布
- STOP 并不是一个词,它是一个结束符
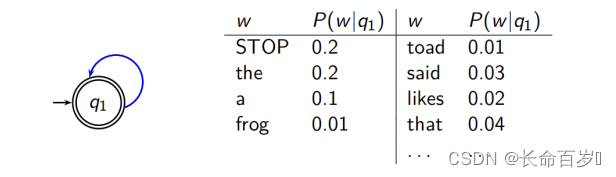
eg:

不同的语言模型(我们将文档看作一个生成查询的语言模型)
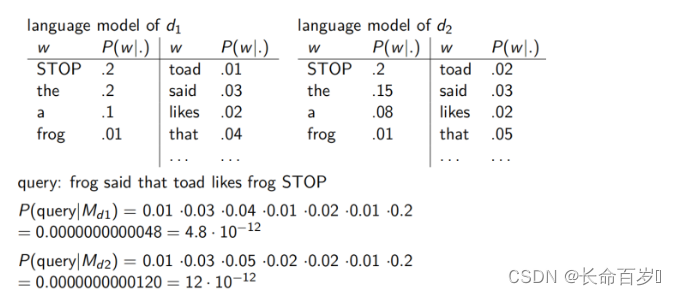
可以看到,对于该查询, P ( q u e r y ∣ M d 1 ) < P ( q u e r y ∣ M d 2 ) P(query|M_{d1}) < P(query|Md2) P(query∣Md1)<P(query∣Md2) 。因此,文档 d 2 d_2 d2 与查询的相关性更大
IR中的语言模型
IR中最早使用也是最基本的语言模型是查询似然模型
查询似然模型
每个文档都被看作一个语言模型(d -> M d M_d Md)。检索的目标是按照其与查询相关的概率 p ( d ∣ q ) p(d|q) p(d∣q) 进行排序。
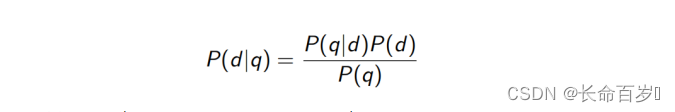
-
p ( q ) p(q) p(q) 对所有文档来说是一样的,所以可以忽略
-
p ( d ) p(d) p(d) 是先验概率,我们常常将其视为对所有文档是相同的
- 我们也可以对高质量文档赋予更高的先验概率
-
p ( q ∣ d ) p(q|d) p(q∣d) 是文档 d 在对应语言模型下,生成 q 的概率
我们按照 p ( d ∣ q ) p(d|q) p(d∣q) 排序,实际上就是按照查询似然 p ( q ∣ d ) p(q|d) p(q∣d) 进行排序。
如何计算 p ( q ∣ d ) p(q|d) p(q∣d) 呢?
计算 p ( q ∣ d ) p(q|d) p(q∣d)
等价于多项式朴素贝叶斯模型(基于条件独立假设)

- 其实前面还有一个系数 K q K_q Kq ,但是对于一个特定的查询,它是一个常数,因此被忽略
我们可以将上式转化为
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FHdugd5E-1670240021845)(C:\Users\nishiyu\AppData\Roaming\Typora\typora-user-images\image-20211228201737438.png)]](https://img-blog.csdnimg.cn/104a49afc38c481ca8069770313d77c1.png)
如何得到 p ( t ∣ M d ) p(t|M_d) p(t∣Md)?
查询生成概率的估计
在最大似然估计及一元语言模型假设的情况下
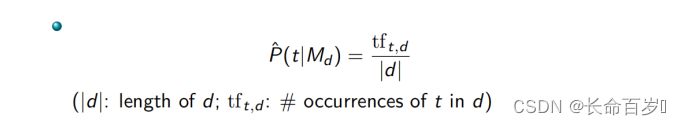
问题:
- 该模型有一票否决权。即,若查询中出现了文档 d d d 中没有的词,概率为 0
- 对文档中出现的词的估计有问题,特别是那些在文档中只出现一次的词往往会被过度估计(一次出现在一定程度上出于偶然性)
解决上述两个问题的方法是平滑
平滑
不仅仅是为了避免零概率,实际上实现了词项权重计算的主要部分
想法:对非零的概率结果进行折扣,对未出现的词的概率赋予一定的值
在一般的参照概率分布中,文档中未出现的查询项都可能在查询中出现,它的概率在某种程度上接近但不可能超过整个文档集中偶然出现的概率。
也就是说,若 t f t , d = 0 tf_{t,d} = 0 tft,d=0,那么 $\hat{P}\left(t \mid M_{d}\right) \le \frac{\mathrm{cf}_{t}}{T} \$
- c f t cf_t cft 是 t 在整个文档集中出现的次数
- T 是所有文档集中词条的个数
Jelinek-Mercer 平滑
将基于文档的多项式分布和基于全部文档集估计出的多项式分布相混合,这类模型称为线性插值语言模型

- 基于全部文档集估计出的多项式分布
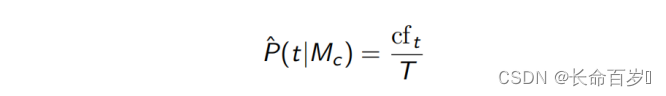
-
M c M_c Mc 是基于全部文档集构造的语言模型
-
如何设置正确的 λ \lambda λ 是获得良好性能的关键
- 取大值:倾向于检索包含所有查询词的文档
- 取小值:适用于长查询。较小的 λ \lambda λ 意味着更平滑(似然估计的概率贡 献更小)
上面是对一个词的平滑,对整个查询的平滑就是乘积
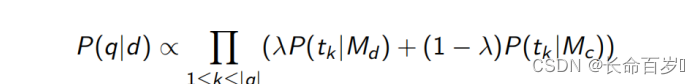
Dirichlet 平滑
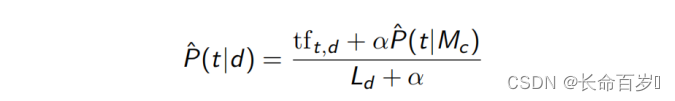
- P ^ ( t ∣ M c ) \hat{P}(t|M_c) P^(t∣Mc) 是 P ^ ( t ∣ d ) \hat{P}(t|d) P^(t∣d) 的先验
- 我们将 P ^ ( t ∣ M c ) \hat{P}(t|M_c) P^(t∣Mc) 设置为 P ^ ( t ∣ d ) \hat{P}(t|d) P^(t∣d) 的初始值
- 当我们阅读一篇文档时,我们根据文档内容,更新 P ^ ( t ∣ d ) \hat{P}(t|d) P^(t∣d)
- 若 α = 0 \alpha = 0 α=0,则相当于没进行平滑, α \alpha α 越大,先验概率的权重就越大,也就越平滑
两种平滑的对比
- 前一种在冗余查询上表现更好,后一种在关键词查询上效果更好
- 两种模型都对平滑参数很敏感,不能在没调参的情况下使用这两种模型
向量空间 VS BM25 VS LM
-
向量空间模型是基于相似度的,是几何 / 线性代数的概念。其余两个都是基于概率论的
-
t f tf tf在三个模型中都用了
- L M LM LM:直接使用 t f tf tf
- 其他两个使用得更复杂一点
-
d f df df
- 在BM25和向量空间中都直接使用了
-
L
M
LM
LM:混合
t
f
tf
tf 和
c
f
cf
cf,与
i
d
f
idf
idf 有类似的效果
- 在一般集合中罕见的词项,但是在一些文档中很常见,将会对排名产生很大的影响
-
c f cf cf
- 只有 L M LM LM 使用了 c f cf cf,其他的都是用的 d f df df
- c f cf cf是基于整个集合的, d f df df以文档为单位的
-
长度归一化
- 向量空间:余弦或主元归一化
- L M LM LM:概率是固有的长度归一化
- B M 25 BM25 BM25:优化长度归一化的参数
理论基础的对比,使用指标的对比,长度归一化的对比