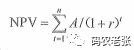本系列文章主要对Bug类路径规划算法的原理进行介绍,在本系列的第一篇文章中按照时间顺序梳理了自1986年至2018年Bug类路径规划算法的发展,整理了13种BUG系列中的典型算法,从本系列的第二篇文章开始依次详细介绍了其中具有代表性的BUG1、BUG2、Tangent BUG、I-BUG、RandomBug、BugFlood等算法。本系列文章谢绝任何形式的转载
本篇文章作为本系列文章第六篇文章,主要对BugFlood算法进行介绍
本系列其他文章见:BUG系列路径规划算法原理介绍——总结篇
一、BugFlood 算法的提出背景
bug算法常使用向目标移动,直到检测到障碍物为止,以及跟随障碍物边界绕行这两种基本运动行为的组合来寻找可行路径。但是这种bug算法可能会选择更长的路线,而且在离开障碍物之前可能需要探索完整的障碍物边界。之所以出现这些缺陷,是因为该bug算法是一个正在探索未知环境以找到通往目标的路径的机器人。但是,我们能否在已知环境中使用这种简单的bug算法呢?
基于以上问题,Nishant Sharma和Shivam Thukral等人与2018年在论文《A virtual bug planning technique for 2D robot path planning》中提出了BugFlood 算法。
论文链接:A virtual bug planning technique for 2D robot path planning
BugFlood算法期望达到的效果: ① 一种快速路径规划算法,该算法可生成接近最优的路径,但时间较少。 ②保证路径长度和完整性,③快速确定路径是否不存在
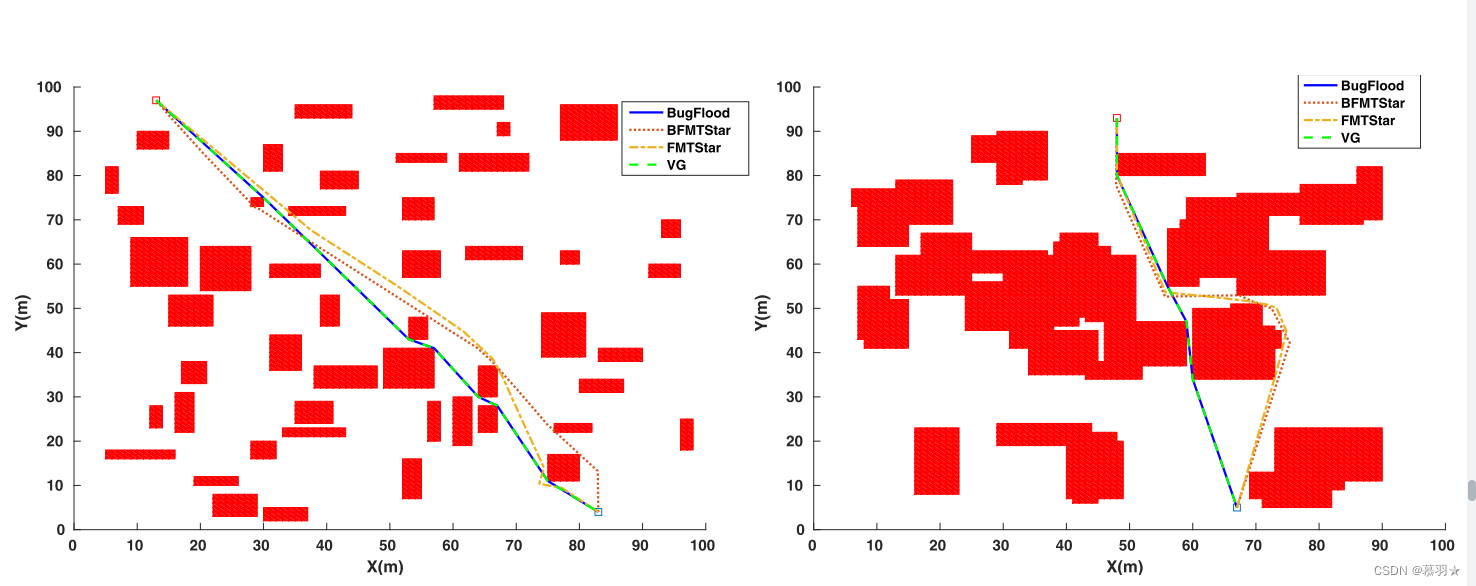
注1:前面的几篇文章介绍的BUG1、BUG2、Tangent BUG、I-BUG、 Randombug等算法都是机器人边移动边规划的,不需要使用先验的环境信息,由机器人搭载传感器实时对环境进行感知,适合用于未知环境中的规划或局部路径规划,而本文介绍的BugFlood 算法是需要具备先验的环境信息的,不是边走边规划的,更适合作为全局路径规划算法使用。
注2:本文示例图片来源于以上论文
二、问题描述
如下图所示的场景机器人位于起点S,需要环境信息已知的情况下找到通往目标T的路径。障碍物空间用O表示,n个障碍物表示为Oi,i = 1,2,… ,n。障碍物可以是任何形状和大小。每个障碍Oi由一组节点vj ∈ Vi表示,j = 1,… ,| Vi |。设pi为第i个障碍物的周界。机器人上的传感器,可以检测r_s米范围内的障碍物。假设机器人使用点质量模型,并将其运动建模为单个积分器模型,即满足下式
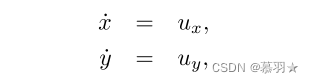
我们还需要了解一些定义:
(1)撞击点(Hit Point): 当机器人沿直线向目标移动并在点P与障碍物接触时,我们将点P定义为撞击点H。
(2)离开点((Leave point):机器人检测到目标,并离开障碍物边界的点被定义为离开点L。
(3)障碍物跟随行为b2: 机器人跟随障碍物边界从撞击点H到离开点L。
(4)路径定义为命中点,障碍节点和离开点的组合,表示为 π = {L_0,H_B, V_i,L_B’ ,H_B ’ ’ ,… ,T},i ∈ O。 (不太清楚论文作者为啥喜欢用π表示路径,这个π可能是希腊字母中的Pi)
其中B表示虚拟机器人B,B’表示由虚拟机器人B产生的虚拟机器人B’,由虚拟机器人B创造的撞击点H_B和由虚拟机器人B’创建的离开点L_B’之间的路径可以由障碍物Oi的几个节点V_i组成。
路径的最后一个分量是目标T,而第一个离开点L0是开始位置S。为了使索引更简单,假设所有具有奇数索引号的机器人将从撞击点向障碍物的左侧探索,而具有偶数索引号的机器人将在障碍物的右侧探索。环境中的活动的机器人表示为A。如果A 为空集﹐ 则环境中没有的机器人。
(5)机器人路径 π(B) 表示机器人B从其当前位置到起点S的路径。
(6)令 π(v_i,B) 表示机器人 B从节点v_i到S的路径。
(7) 令 π^(v_i) 表示从节点v_i到起始位置S的最短路径,并且 ζ(π ^ (vi)) 是从S到节点v_i的最短路径的长度。
(8)将由机器人Bk产生的机器人Bk+1和Bk+2成为机器人B的子代机器人,机器人Bk称为机器人Bk+1和Bk+2的父代机器人。
三、BugFlood算法的绕行策略
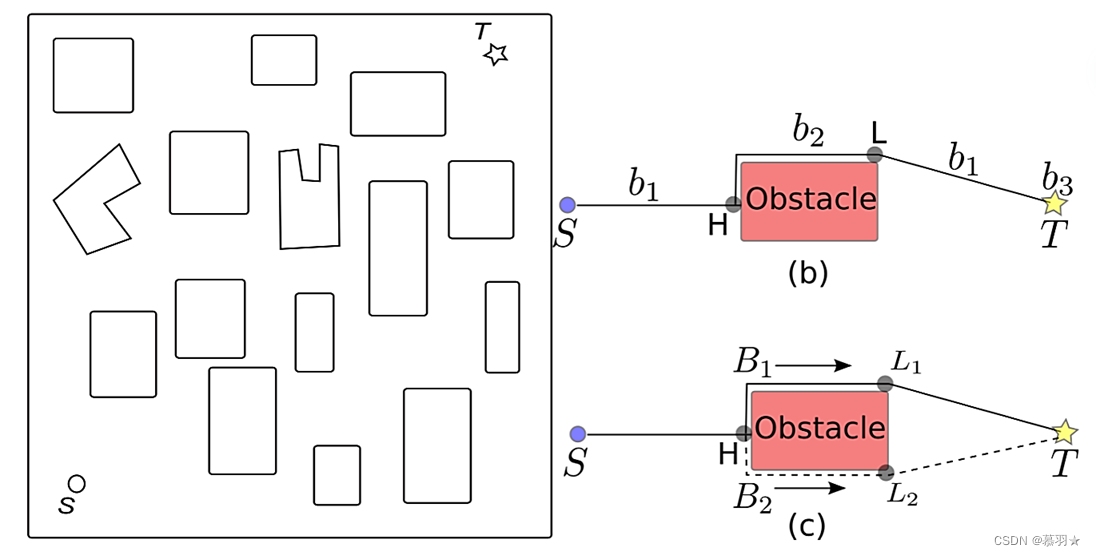
BugFlood算法具有三种行为: (b1) 沿直线向目标移动,(b2) 跟随障碍物边界,(b3) 停止。

对于上图中所描述的场景中,假设一个机器人从S出发,向T移动,当它检测到感应范围内的障碍物时,它会创建一个撞击点H。如果采用传统的绕行障碍物策略,比如说始终左转,则机器人将从左侧开始跟随障碍物边界 (行为b2),直到到达可以看到目标的点 (离开点L)。此时,机器人由行为b2变为行为b1,bug朝着目标前进。当bug到达目标位置时,则bug停止 (行为b3),如上图中的(b)图所示。
与传统的绕行策略不同的是,当BugFlood算法创建撞击点H后,会在H处拆分成两个虚拟机器人,分别向左侧和向右侧绕行,如上图中的(c)图所示,当所有的虚拟机器人达到目标点后,将选取他们中路径最优的一个作为BugFlood算法的规划路径。
在BugFlood算法中,虚拟机器人每遇到一个障碍物,就会拆分成两个虚拟机器人,形成一个二叉树结构,当某个虚拟机器人达到了目标后,就追踪其父级来找到从T到S的路线,计算它们的路径成本,并选择成本最低的路径。
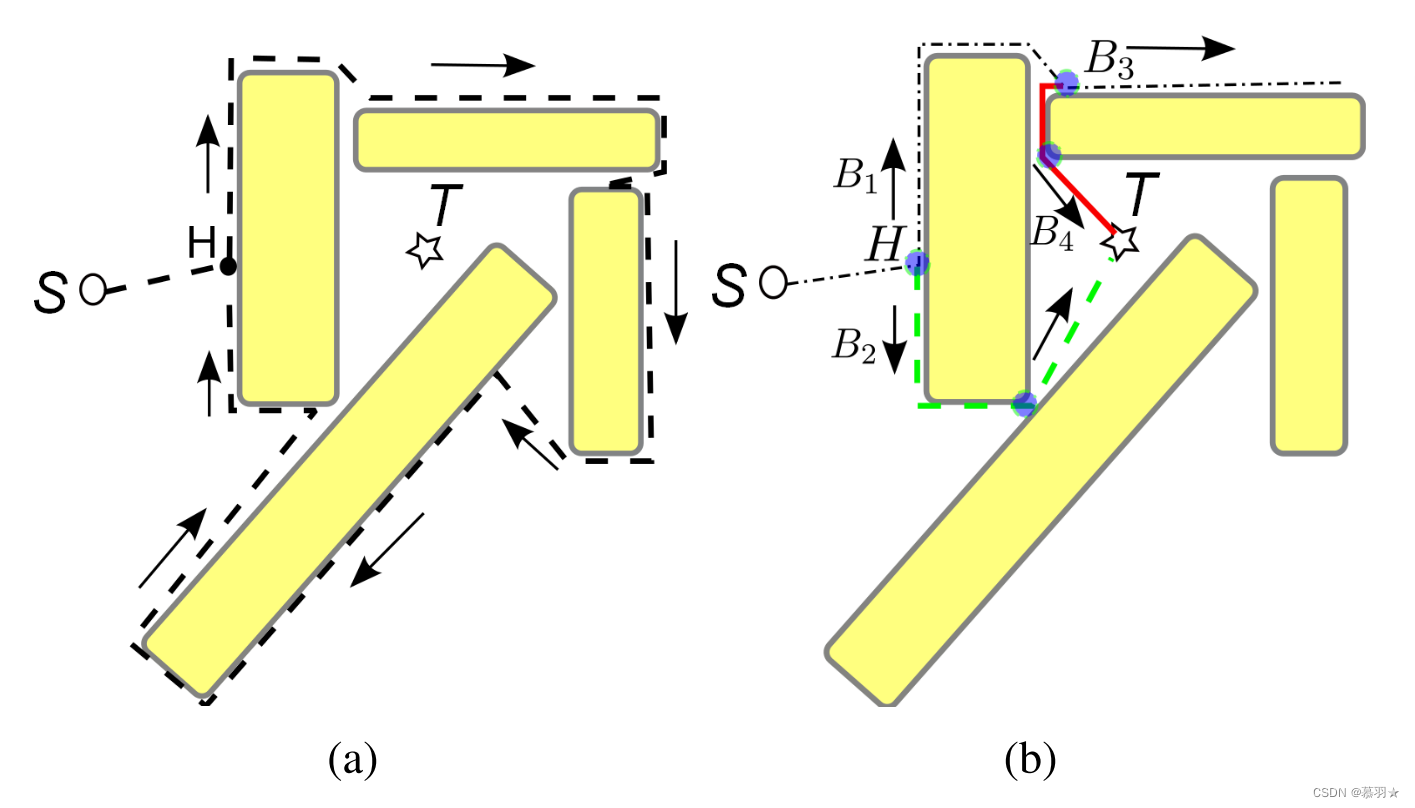
在下图中的例子中,采用传统的固定绕行方向的策略时,比如说始终向左绕行时,可能出现无限循环卡死的情况,如下图中的(a)图所示,而采用BugFlood算法的拆分绕行策略,则可避免该情况发生,如下图中的(b)图所示。
四、BugFlood算法流程
BugFlood算法的流程,在总体框架上分为3步,在step1中机器人朝着目标点直行,在step2中机器人绕行障碍物,循环执行step1和step2,直到在step1中没有可以移动的机器人(所有可以达到目标点的机器人已到达目标点),则跳转至step3进行路径回溯,并选取其中最优的路径作为规划路径,结束规划。
接下来详细的展开介绍:
(1)Step0:
执行一些初始化操作,创建第一个虚拟机器人(下面均简称为机器人),编号为k=0,并将其放入集合A中,并将编号为k=0的机器人的撞击点初始化为0,离开点初始化为起始点S,父代机器人设为空。
关键变量梳理:集合A中存放的是当前所有可以执行朝目标点移动的直行行为机器人,集合H中存放的是当前所有可以执行绕行障碍物行为机器人,集合E中存放的是所有已经达到目标点的机器人(伪代码中是用希腊字母Β表示的,但为了与代表机器人的英文字母B区分,本文中改用E来表示该集合),当前操作的机器人用B表示,其编号用k表示。
(1)Step1:直行
对于每个集合A中的机器人执行以下操作:
①当前机器人B朝着目标点直行直至发生下面两种情况之一,转而执行对应的操作②。
② —情况a ,当前机器人到达了目标点T,则将当前机器人的撞击点设置为T,将当前机器人放到集合E中,并将其在集合A中删除,判断此时集合A是否为空,若为空则说明没有可以进行直行的机器人,规划已完成跳转至Step3进行路径回溯,并选取最佳路径。若集合A不为空,则继续对集合A中的下一个机器人执行操作①
② —情况b ,遇到障碍物Oi,产生撞击点H_B,并将当前机器人的撞击点设置为H_B,产生两个新的机器人编号为k+1、k+2,并将其放到集合H中,并将这两个新产生的机器人的撞击点初始化为H_B,父代机器人设置为当前的机器人B,将机器人编号累计变量k加2,将当前的机器人B从集合A中移除,继续对集合A中的下一个机器人执行操作①
③ 当集合A中所有机器人均完成以上操作后,转而执行Step2
(2)Step2:绕行
对于每个集合H中的机器人执行以下操作:
① 当前机器人B跟随障碍物边界移动直至以下两种情况之一发生,转而执行对应的操作②
② —情况a ,机器人发现目标点T(即伪代码中的T is in LOS),创建一个临时的离开点L’_B,创建T与L’_B之间的连线L,判断L与机器人B之前的路径是否相交。
情况a分支一: 若相交,则说明在此处不能通过直行前往目标点,则跳转至操作①继续对当前机器人B执行绕行障碍物操作,如下右图所示:

情况a分支二: 若不相交,则创建离开点L_B,并将机器人B的离开点设为L_B,将机器人B添加至集合A中,并将其从集合H中移除,则继续对集合H中的下一个机器人执行操作①
② —情况b ,机器人绕行到当前障碍物Oi的某个顶点vj,判断Vindex(vj)是否为空。 (Vindex(vj)中储存这曾经到达过障碍物Oi的当前顶点Vj的机器人,且vDistance(vj)中储存着曾经到达过顶点vj的机器人从起点S到顶点vj的路径距离)
情况b分支一:如果为空,说明之前没有机器人到达过该顶点,则将当前机器人B记录在Vindex(vj)中,并将当前机器人B从起点S到顶点vj的路径长度记录在vDistance(vj)中。跳转至操作①继续对当前机器人B执行绕行障碍物操作。
情况b分支二:如果不为空,说明之前已经有机器人到达过该顶点,则需要进一步判断:
情况b分支二(1):若当前机器人B从起点S到达该顶点vj的路径长度小于之前的机器人从起点到顶点vj的路径长度,则将当前机器人B记录在Vindex(vj)中,并将当前机器人B从起点S到顶点vj的路径长度记录在vDistance(vj)中 ,按照论文中描述的思想,此时会用机器人B从起点S到顶点vj的路径来对之前那个机器人的此部分路径更新替换(该操作在伪代码中没有体现) ,然后机器人将机器人B从H中移除,并将机器人B抛弃。继续对集合H中的下一个机器人执行操作①
情况b分支二(2):若当前机器人B从起点S到达该顶点vj的路径长度大于之前的机器人从起点到顶点vj的路径长度,则直接将当前机器人B从H中移除,并抛弃。继续对集合H中的下一个机器人执行操作①
③ 当集合H中所有机器人均完成以上操作后,转而执行Step1
(3)Step3:路径回溯
对于每个集合E中的机器人执行以下操作:
将当前机器人B中存储的路径提取出来储存到π中,然后将机器人B的父代机器人B中存储的路径提取出来添加到π中,以此循环,直至π中最后一个路径点是起点S时,则当前机器人的路径回溯完成,开始对E中的下一个机器人执行路径提取操作
当集合E中所有机器人均完成以上操作后,Step3路径回溯提取也就是完成了,伪代码到这里也就结束了,其实论文中还提到了路径修剪操作,按照论文中的说法是放在了Step2中进行的,但是伪代码中并未体现,个人感觉路径修剪属于对已得到的可行路径进行简单的优化操作,可以在得到路径后再进行操作,因此,在本文中我将该操作放到了Step4。
所以接下来跳转到Step4
(4)Step4:路径修剪
对于Step3中得到的每条可行路径执行以下操作:
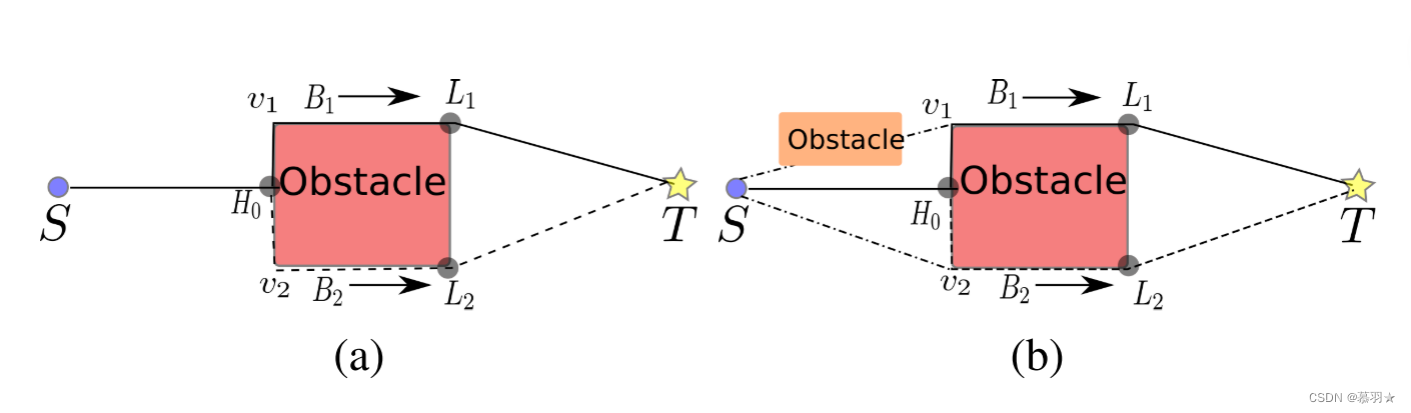
通过沿该路径顺序在两个节点之间构造新的路径段来修剪获得的路径。若新产生的路径段不与障碍物相交则替换掉原有路径段,若与障碍物相交则放弃该路径段。比如在下图的例子中通过Step3提取到①:[S →H0 →v1→L1→T]和 ②:[S →H0 →v2→L2→T]两条路径,对于路径②通过在S和v2直接构建新的路径段S-v2发现不与障碍物相交,则可将路径②优化为[S →v2→L2→T],但是对于路径①,因为S和v1之间存在障碍物,则放弃路径段S-v1的优化。
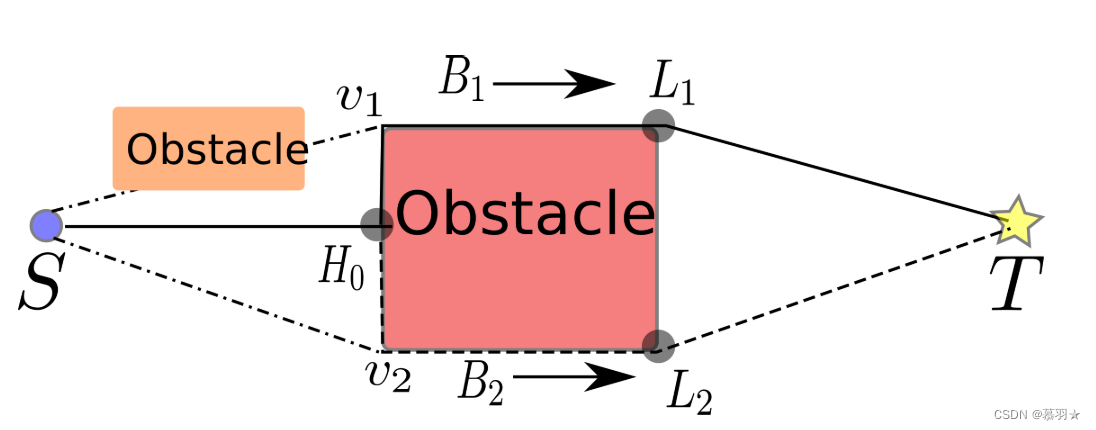
另外一个路径修剪优化前后的效果对比如下图所示:

当Step3中得到的所有路径均完成以上操作后,安装论文中思想,此时需要从优化后的所有可行路径中选择最优的一个作为最终的规划结果(此操作在伪代码中未体现),并结束规划。
五、BugFlood算法伪代码
由于原论文中是按照递进的逻辑进行介绍的,因此没有给出完整的BugFlood算法的伪代码,我通过对论文的理解,将论文中给出的伪代码进行了整理合并,形成了下图所示的伪代码,由于上面介绍的Step4是我的猜想,因此并不包含在下面的伪代码中,Step1~Step3跟我上文的文字介绍非常吻合,有了上文的基础应该很容易看懂。

六、BugFlood算法的一些思考
思考1:Step1中仅用集合A是否为空来作为所有机器人均已完成规划是否是合理的?是否应该考虑集合H的状态?从论文中表达思想是所有机器人都达到目标点后,才执行路径回溯,然后选择其中最优的那个作为规划结果,仅用集合A为空来判断能达到上述效果吗? 比如假设当前集合A中存在n个机器人的,前n-1个机器人均因执行了操作2中的情况b而被从A中移除,很显然由这些机器人产生的子代机器人并没有完成规划,而若此时集合A中的最后一个机器人恰好到达了目标点T执行了情况a,也被从集合A中移除,此时集合A已为空,转而执行Step3结束规划。显然与设想的效果冲突,因此,我感觉在跳转至Step3时需要进一步考虑集合H的状态
思考2:关于Step2中操作② —情况a中提到的机器人发现目标点T时停止绕行的判断策略个人感觉有些混乱,不如前几种BUG算法中的清晰明了,从论文中举的例子来看,当机器人与目标点T直接有障碍物阻挡视线时,论文作者也认为发现了目标点T,难道论文所谓的发现是指机器人与目标点的距离小于某个界限吗? 论文中对于T is in LOS的概念给的相当模糊,即对于目标点可视的概念是不清晰的。
思考3:是否可以这样认为:关于机器人中储存的路径,当机器人位于集合A中时,在执行直行行为前其储存的是从撞击点到离开点的路径,执行直行行为后,其储存的是从离开点到撞击点的路径,当机器人位于集合H时,执行绕行前其其储存的是撞击点,执行绕行行为后储存的是从撞击点到离开点的路径。
七、BugFlood算法特性分析
(1)特性1 :路径长度
BugFlood算法产生的任何机器人的路径长度永远不会超过下式,其中pi是机器人遇到的第i个障碍物的周长,D是S和T之间的欧几里得距离。
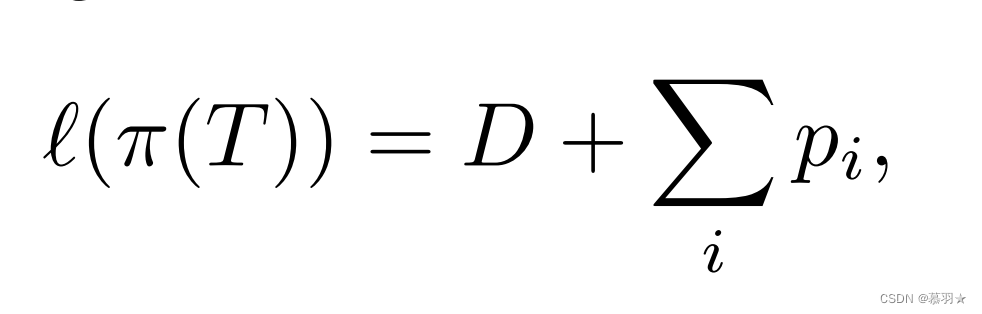
(2)特性2 :bug清理
如果一个机器人 Bk访问了以前被其他一些机器人访问过的节点vj,这个机器人将被终止(被抛弃)。
(3)特性3 :无可行路径
如果机器人 Bk是第一个访问障碍物(凹或凸)Oi的机器人,若由机器人Bk形成的机器人 Bk+1和Bk+2在对障碍物Oi执行障碍物跟随行为的时候被终止,则不存在路径从S到T的路径。
八、BugFlood算法性能
论文中对BugFlood算法以及OMPL库中的PRM* 、RRT、RRT*
、BFMT*、 BIT*、 CForest、FMT* 、IRRT* 等算法进行了实验对比,规划效果如下:
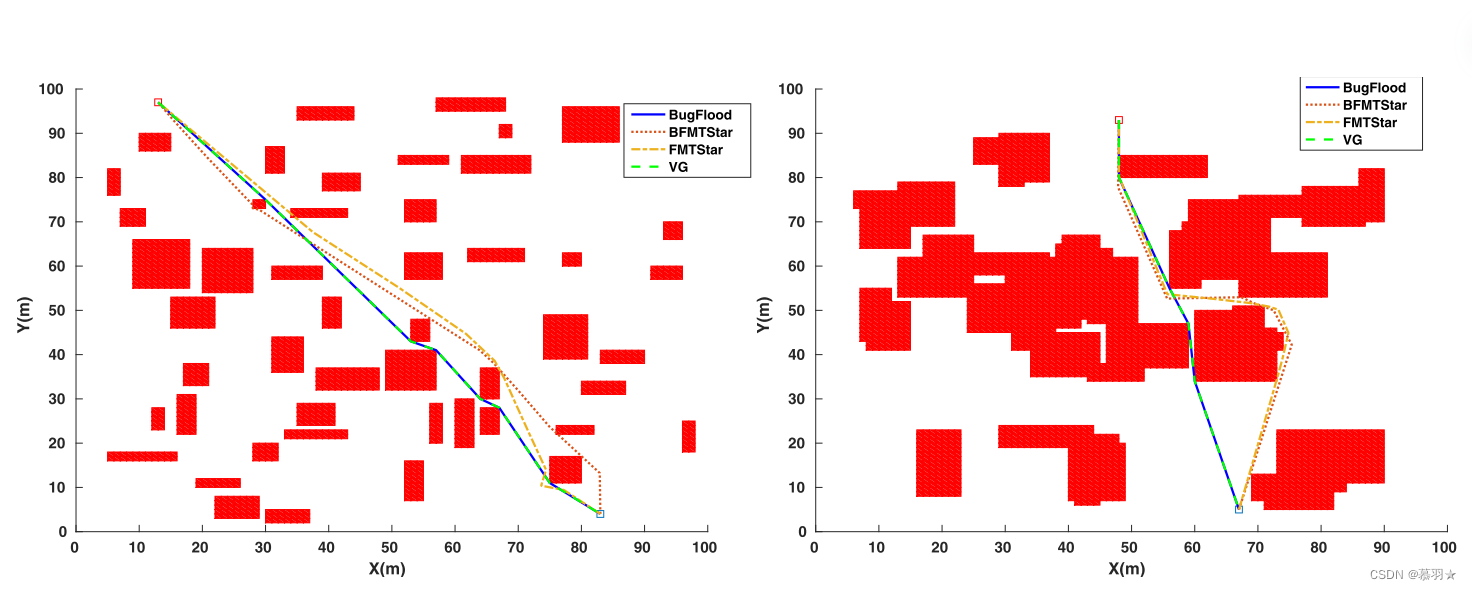
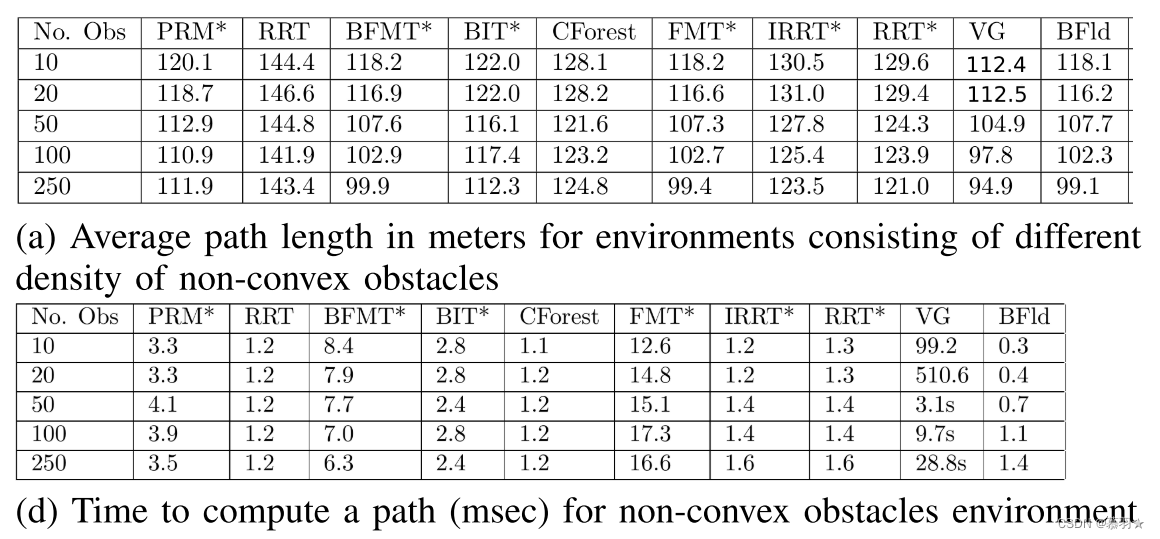
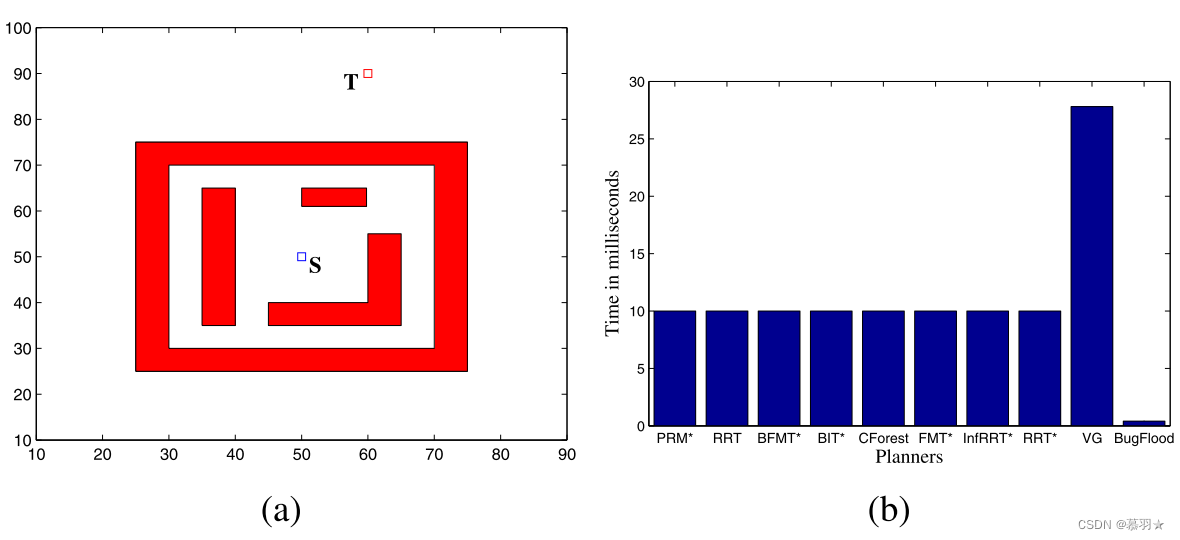
在下面(a)图所示的环境中,以上算法确定无可行路径的耗时如下面(b)图所示。



![[附源码]Python计算机毕业设计Django时间管理软件app](https://img-blog.csdnimg.cn/1102e85e59e34721b863175f794ac78b.png)