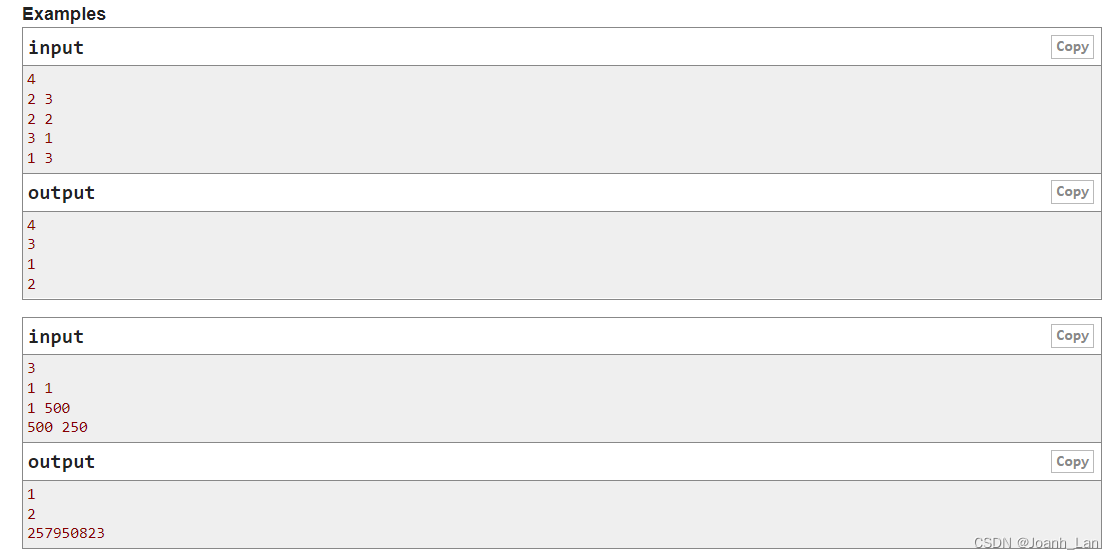
题目如下：

思路 or 题解

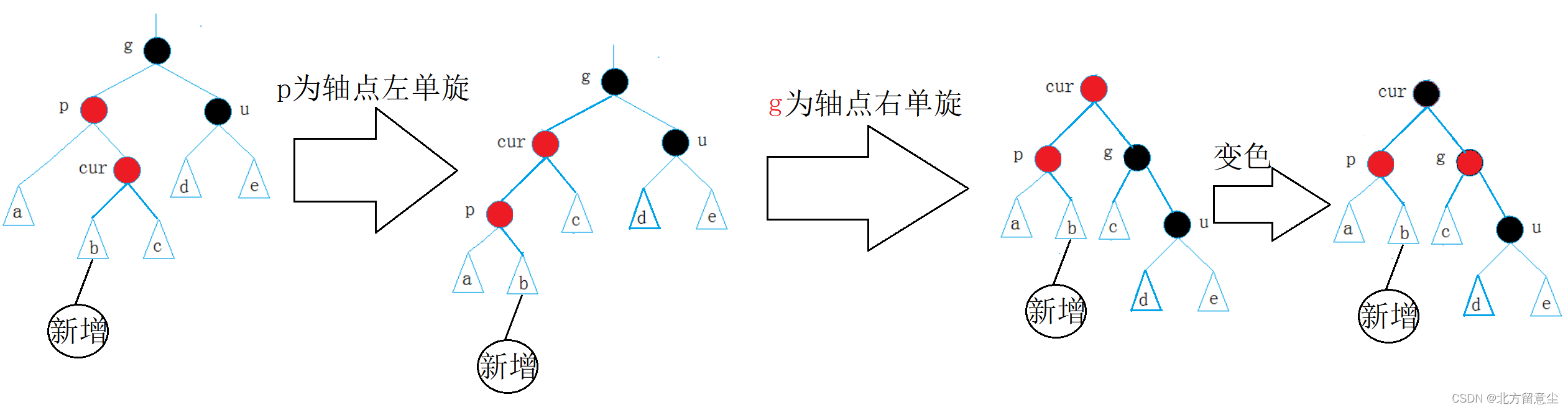
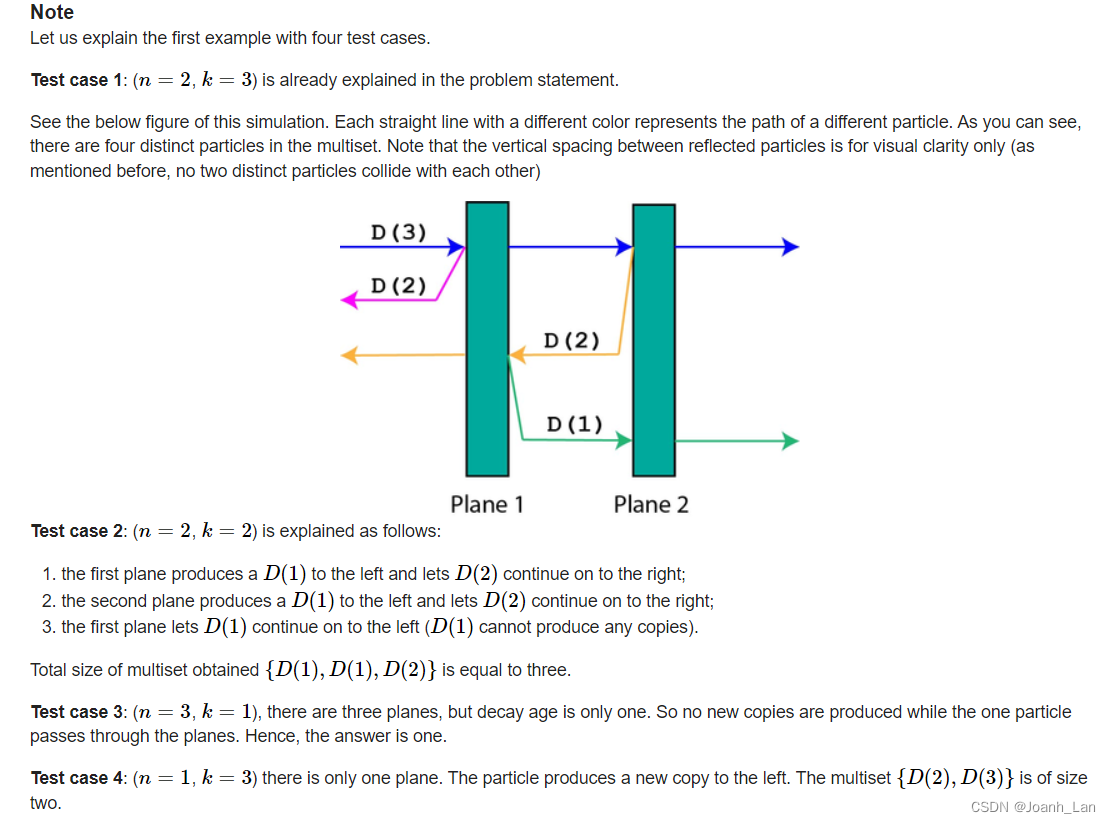
我们可以通过图解发现：可以递推找到答案了
我们约定：$dp[i][j]$
第 $i$ 个板, 衰变年龄为$j$ 的答案是 $dp[i][j]$
我们通过图解找到转移方程：
$dp[i][j]=dp[i-1][j]+dp[n-i][j-1]$
$dp[i][j]$ 的答案数等于：由在穿过这层后，还剩 $i-1$ 个板，衰变年龄为 $j$ 的答案数和往回走，还剩 $n-i$ 个板，衰变年龄为 $j-1$ 粒子答案数的和.

注意一下dp状态的初始化:

for (int i = 0; i <= n; i++)
        dp[i][1] = 1;
    for (int i = 1; i <= k; i++)
        dp[0][i] = 1;

AC 代码如下:

int dp[1009][1009];
int n, k;
void solve()
{
    cin >> n >> k;
    for (int i = 0; i <= n; i++)
        dp[i][1] = 1;
    for (int i = 1; i <= k; i++)
        dp[0][i] = 1;
    for (int j = 1; j <= k; j++)
        for (int i = 1; i <= n; i++)
            dp[i][j] = (dp[i - 1][j] + dp[n - i][j - 1]) % mod;
    cout << dp[n][k] << '\n';
}   
int main()
{
    buff;
    int _;
    cin >> _;
    while (_--)
        solve();
}