思维导图:
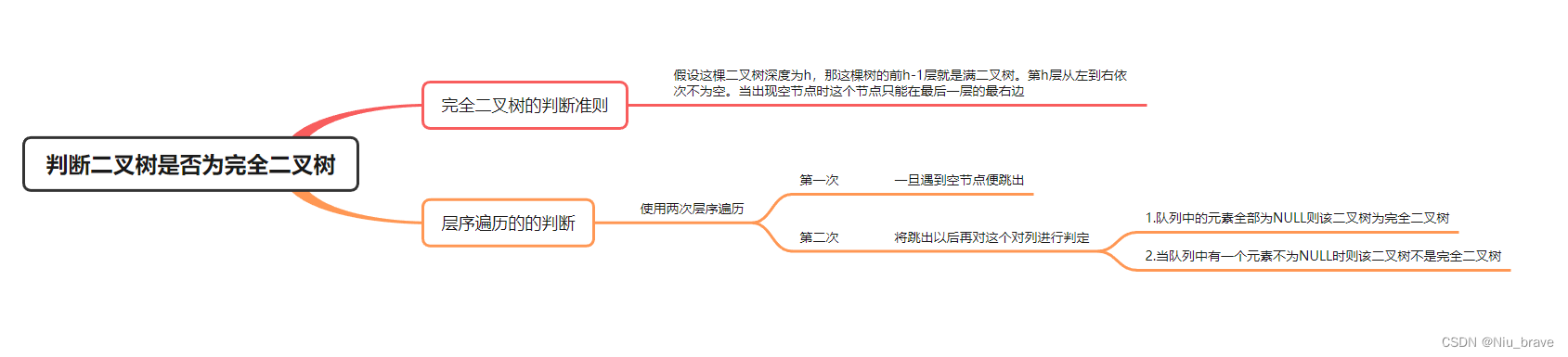
一,完全二叉树的特点
假如我们现在有一颗完全二叉树,那它应该长什么样呢?
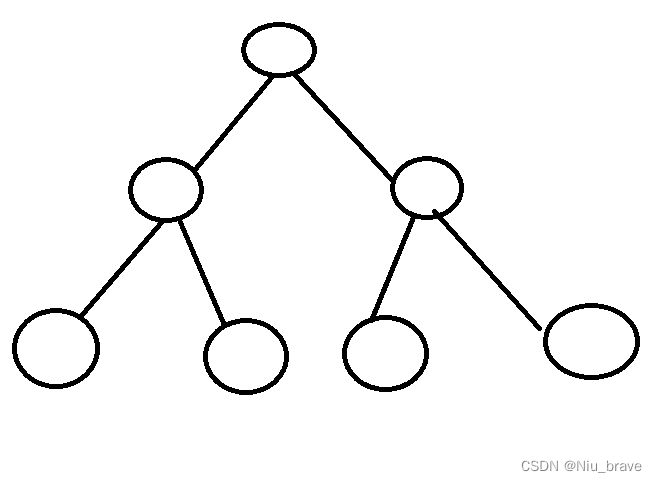
它应该长这样:
这样:
这样:
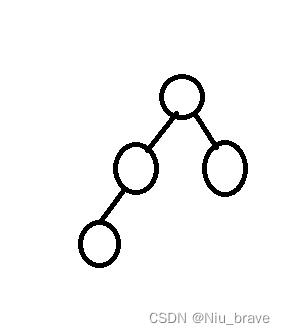
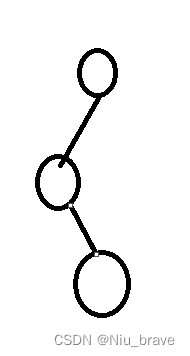
如果不是一颗完全二叉树该长什么样呢?
应该长这样:
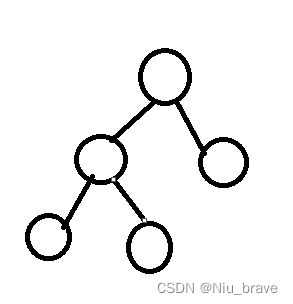
这样:
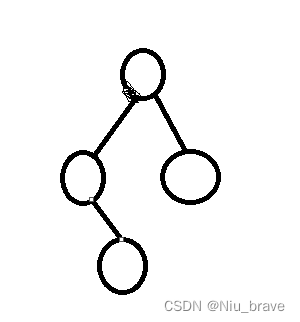
这样:
通过这几个图的对比可以看出完全二叉树与非完全二叉树的区别以及判断的方法:
1.假如一棵二叉树是完全二叉树的话,那这棵树一定符合:
1.前h-1层是一个满二叉树。
2.最后一层从左到右只能在最右边出现空节点。
2.完全二叉树的一个特征:
如果一颗二叉树是完全二叉树那在这棵二叉树中度为1的节点个数只能为1.
二,使用层序遍历来判断的依据
层序遍历的遍历逻辑便是出一层出队列然后带下一城入队列。层序遍历的代码便长这样:
void LevelOrder(BTreeNode* root) { Queue pq;//创建队列 QueueInit(&pq);//初始化队列 if (isEmpty(&pq)) { QueuePush(&pq, root);//往队列中插入树节点 } while (!isEmpty(&pq)) { BTreeNode* front = QueueFront(&pq); printf("%d->", front->val); QueuePop(&pq);//出队列 if (front->left) QueuePush(&pq, front->left);//入下一层树节点 if (front->right) QueuePush(&pq, front->right); } QueueDestory(&pq);//销毁队列 }但这个代码却并不能够直接拿来判断一颗二叉树是否为完全二叉树。所以我们得对这个代码进行改造来实现判断的功能。现在我改造的代码如下:
代码:
bool CompleteBTree(BTreeNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!isEmpty(&q))
{
BTreeNode* front = QueueFront(&q);
QueuePop(&q);
//当该节点为NULL时就跳出该循环到下一循环进行判断
if (front == NULL)
break;
//当树节点的某一子节点为NULL时也需要插入队列中
QueuePush(&q,front->left);
QueuePush(&q,front->right);
}
while (!isEmpty(&q))
{
BTreeNode* front = QueueFront(&q);
QueuePop(&q);
//若该队列中的元素不完全是NULL节点那这棵二叉树就不是完全二叉树
if (front)
{
QueueDestory(&q);
return false;
}
}
QueueDestory(&q);
return true;
}1. 在写这个判断的函数时我主要按照层序遍历的代码改了几处地方,第一处便是这里:
if (front == NULL) break;因为我们要判断的是完全二叉树,所以NULL节点只能在最后一层出现。所以当该二叉树为完全二叉树时并且出现了NULL的节点那该节点所在层就是最后一层(即使不是也要默认是最后一层)。
2.第二处便是添加了一个判断条件。代码如下:
while (!isEmpty(&q)) { BTreeNode* front = QueueFront(&q); QueuePop(&q); //若该队列中的元素不完全是NULL节点那这棵二叉树就不是完全二叉树 if (front) { QueueDestory(&q); return false; } } QueueDestory(&q); return true;这段代码的作用就是对跳出来后的队列内的元素进行分析,假如这个队列里面出现了不是NULL的节点,那这棵二叉树便不是完全二叉树。
三,算法实现图解
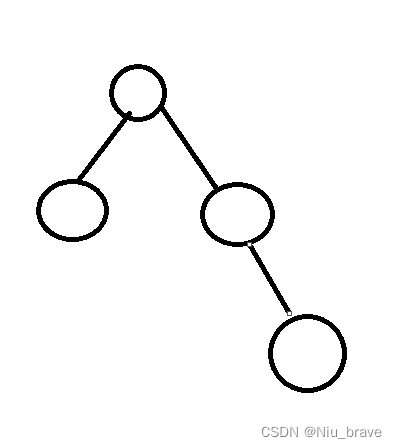
现在我们利用这个判断代码对这棵二叉树:
先说结论:这不是一颗完全二叉树。
那在代码中是怎么走的呢?
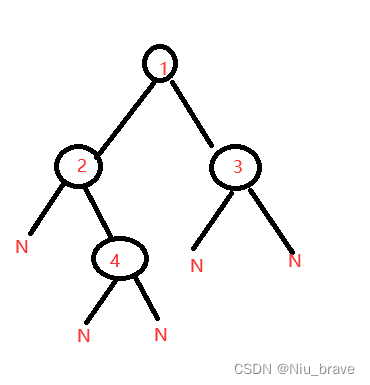
代码图解:
这个图便表示的是代码:
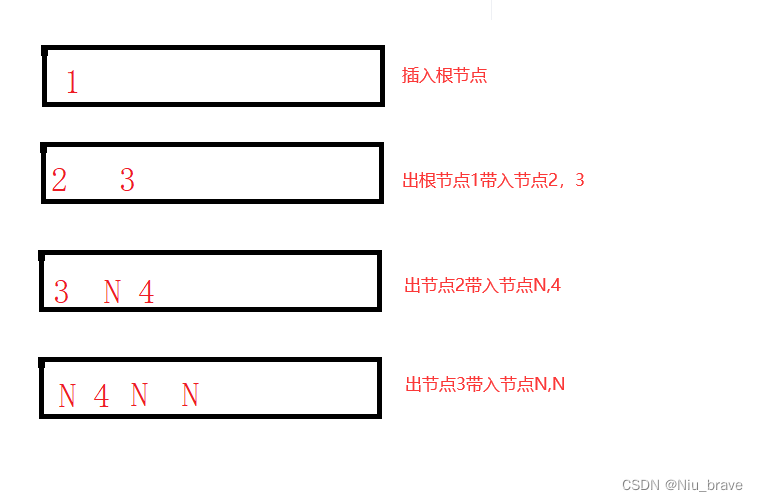
while (!isEmpty(&q)) { BTreeNode* front = QueueFront(&q); QueuePop(&q); //当该节点为NULL时就跳出该循环到下一循环进行判断 if (front == NULL) break; //当树节点的某一子节点为NULL时也需要插入队列中 QueuePush(&q,front->left); QueuePush(&q,front->right); }走的过程以及执行的操作。当这段代码走完以后,队列就变成了这样:
然后使用代码:
while (!isEmpty(&q)) { BTreeNode* front = QueueFront(&q); QueuePop(&q); //若该队列中的元素不完全是NULL节点那这棵二叉树就不是完全二叉树 if (front) { QueueDestory(&q); return false; } } QueueDestory(&q); return true;进行判断,在走第二次循环的时候front = 4这个节点的地址为true。所以代码:
if (front) { QueueDestory(&q); return false; }执行,返回false。