前言：

本篇将是最后一篇我们利用栈与队列来解决力扣问题，在下文我们将进入到数这一章，相对应的【夜深人静讲数据结构与算法】专栏中树也会及时更新。

 347. 前 K 个高频元素 - 力扣（LeetCode）

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

 1.哈希表暴力解法：

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
    // 使用哈希表统计每个元素的出现频率
    unordered_map<int, int> frequency;
    for (auto num : nums) {
        frequency[num]++;
    }

    // 使用桶排序，将出现次数相同的元素放入同一个桶中，并记录出现次数
    vector<vector<int>> buckets(nums.size() + 1);
    for (auto item : frequency) {
        buckets[item.second].push_back(item.first);
    }

    // 从后往前遍历桶，获取出现频率最高的 k 个元素
    vector<int> res;
    for (int i = buckets.size() - 1; i >= 0 && res.size() < k; i--) {
        for (auto elem : buckets[i]) {
            res.push_back(elem);

            if (res.size() == k) {
                break;
            }
        }
    }

    return res;
}
};

我们以1 1 1 2 2 3 为例：
第一步：使用哈希表统计每一个元素的出现频率

第二步：使用桶排序，把出现次数相同的元素放入到一个桶里面，并记录出现次数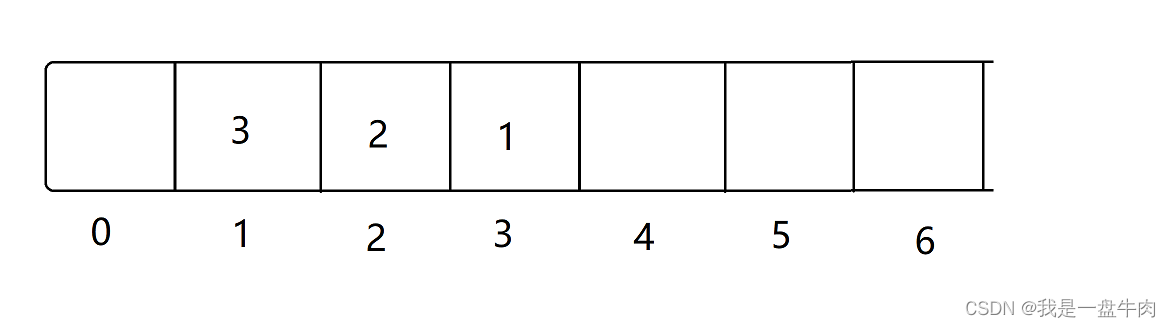

详细的来说，我们以出现的次数value为下标，将数字key值放到桶里面。

第三步 .从后向前遍历，获取出现频率最高的k个元素。

因此此时下标就是次数，下标越大出现的次数就越大。因此我们从后向前遍历.

如果下标对应的元素不为0，（出现了符合出现下标次数的元素），我们就输出。

这样就完成了输出整个数组前n个高频数字。

---

我们可以看出使用哈希数组会对空间造成明显的浪费，因此我们一般倾向于使用第二种算法：

解法2：运用顶堆解法

        大顶堆和小顶堆是两种常见的堆数据结构，都是二叉树形式的数据结构。它们的不同点在于节点之间的大小关系不同。 

        大顶堆是指对于一个父节点，其左右子节点的值都小于等于它的值。也就是说堆顶元素是最大值，在一个大顶堆中，任何一个父节点都比它的子节点大。 

        小顶堆是指对于一个父节点，其左右子节点的值都大于等于它的值。也就是说堆顶元素是最小值，在一个小顶堆中，任何一个父节点都比它的子节点小。 

        堆的操作包括插入、删除和获取堆顶元素等，这些操作都可以在时间复杂度 O(log n) 内完成。它常用于在动态数据中快速找到最大值或最小值，例如快速排序、优先队列等算法和数据结构中。

我们让堆里面就维持k个元素，例如求一个数字中的高频前k个，一般人的思路是：我们就利用大顶堆遍历数组，堆始终维持k个元素，那么最后我们直接输出这个堆顶的所有元素，就可以遍历。但实际上我们要用小顶堆，因为顶堆的top元素只能从堆顶弹出，而我们大顶堆的堆顶元素永远都是最大的，也就是我们如果弹出就会把大元素弹出，因此我们采用小顶堆，一直弹出最小的两个元素，那么我们最后就会得到K个元素。

 这种堆的数据结构是二叉树，而我们整体只需要遍历一次，也就降低了时间复杂度和空间复杂度。

而c++中并没有直接为我们提供堆顶这种数据结构，但是给我们提供了一种底层是大顶堆或者小顶堆的数据结构:优先队列：

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> freq;
        for (auto num : nums) {
            freq[num]++;
        }
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        for (auto iter : freq) {
            pq.push({ iter.second, iter.first });
            if (pq.size() > k) {
                pq.pop();
            }
        }
        vector<int> res(k);
        for (int i = k - 1; i >= 0; i--) {
            res[i] = pq.top().second;
            pq.pop();
        }
        return res;
    }
    
};

priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq    的意思：

这是一个使用 STL 中 priority_queue 实现的小顶堆，元素类型为 pair<int, int>，即由一个整型元素和一个对应的出现次数组成的 pair 类型。

priority_queue 的三个参数分别为：

• - 元素类型：pair<int, int>，表示存放元素的数据类型。
• - 底层容器类型：vector<pair<int, int>>，表示使用一个 vector 来存储堆中的元素。
• - 比较函数类型：greater<pair<int, int>>，表示使用一个以 greater 为比较准则的比较函数来实现堆。

其中，greater 表示从大到小排序，而 less 表示从小到大排序。由于我们在找出出现频率最高的前 k 个元素时需要使用小顶堆，这里使用 greater 作为比较准则，即按照出现频率从小到大排序。

 227. 基本计算器 II - 力扣（LeetCode）

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

整数除法仅保留整数部分。

你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。

这道题的难点就在于编译器在处理运算式子的时候，总是以从左到右的顺序来进行计算的，而忽略了运算符号的优先级，因此本题实际上是在想办法设计处一种算法来处理运算符号的优先级，实际上这种方法已经被人发现了，那就是利用逆波兰表达式。我们先把式子转换成为逆波兰表达式，然后再写逆波兰表达式的计算规则，我们就可以解决此题，而我也有对逆波兰转换进行介绍的文章，里面详细介绍了如何转化为逆波兰表达式以及逆波兰表达式如何进行计算。

【夜深人静学数据结构与算法 | 第二篇】后缀（逆波兰）表达式

class Solution {
public:
    int calculate(string s) {
             stack<int> nums;
    stack<char> ops;
    unordered_map<char, int> prec = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
    int num = 0;
    for (int i = 0; i < s.size(); ++i) {
        if (isdigit(s[i])) {
            num = num * 10 + (s[i] - '0');
            if (i == s.size() - 1 || !isdigit(s[i + 1])) {
                nums.push(num);
                num = 0;
            }
        } else if (s[i] == '(') {
            ops.push('(');
        } else if (s[i] == ')') {
            while (ops.top() != '(') {
                char op = ops.top(); ops.pop();
                int num2 = nums.top(); nums.pop();
                int num1 = nums.top(); nums.pop();
                if (op == '+') nums.push(num1 + num2);
                else if (op == '-') nums.push(num1 - num2);
                else if (op == '*') nums.push(num1 * num2);
                else if (op == '/') nums.push(num1 / num2);
            }
            ops.pop(); // 把左括号弹出
        } else if (prec.count(s[i])) {
            while (!ops.empty() && ops.top() != '(' && prec[s[i]] <= prec[ops.top()]) {
                char op = ops.top(); ops.pop();
                int num2 = nums.top(); nums.pop();
                int num1 = nums.top(); nums.pop();
                if (op == '+') nums.push(num1 + num2);
                else if (op == '-') nums.push(num1 - num2);
                else if (op == '*') nums.push(num1 * num2);
                else if (op == '/') nums.push(num1 / num2);
            }
            ops.push(s[i]);
        }
    }

    while (!ops.empty()) {
        char op = ops.top(); ops.pop();
        int num2 = nums.top(); nums.pop();
        int num1 = nums.top(); nums.pop();
        if (op == '+') nums.push(num1 + num2);
        else if (op == '-') nums.push(num1 - num2);
        else if (op == '*') nums.push(num1 * num2);
        else if (op == '/') nums.push(num1 / num2);
    }

    return nums.top();
    }
};

注意点：
`isdigit` 是 C++ 中用来判断一个字符是否是数字的函数。它的底层实现是通过比较字符的 ASCII 码来判断的。

函数原型为：

int isdigit(int c);

它的参数是一个字符，如果这个字符是一个数字，则返回非零值，否则返回 0。需要包含头文件 #include <cctype>` 才能使用 `isdigit` 函数。

总结：

        合理的利用栈与队列可以解决一些看似棘手的问题，因此我们要学好栈与队列两个数据结构，才可以更好的玩转算法

今天的内容到这里就结束了，感谢大家的阅读。

如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！