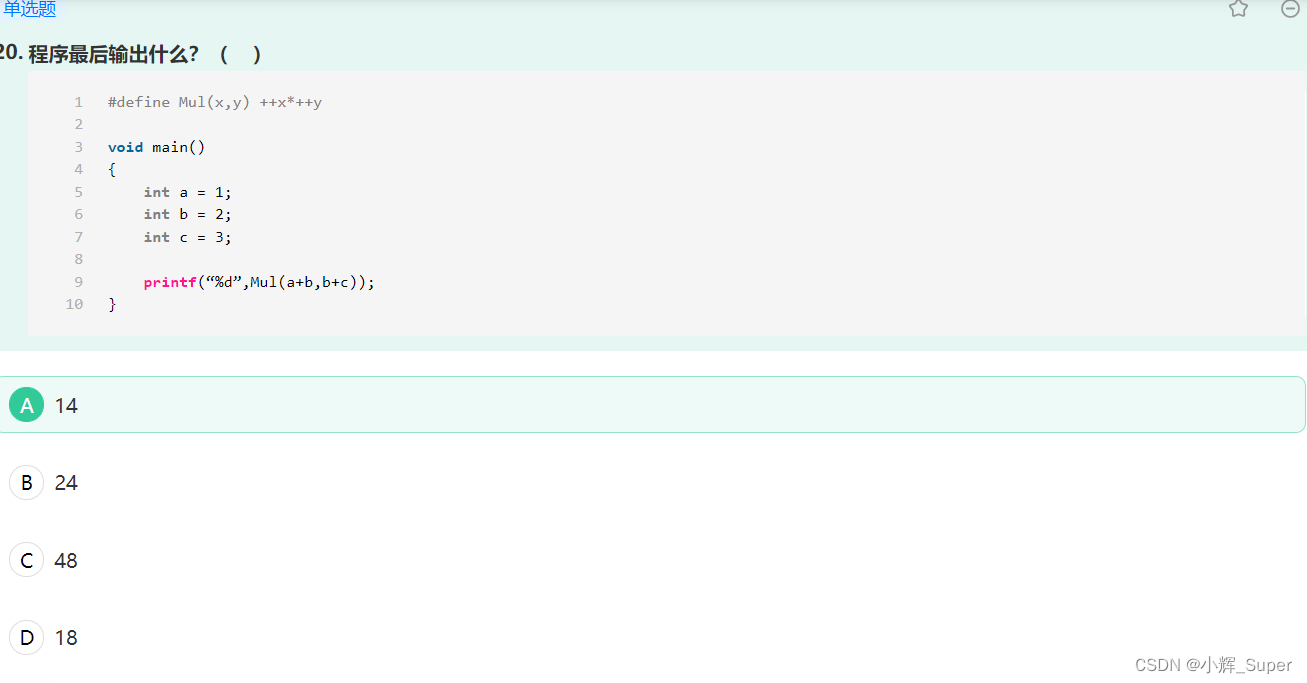
计算机视觉算法——BEV Perception算法总结

最近读了一篇2022年刚发的BEV Perception算法的总结《Vision-Centric BEV Perception: A Survey》，感觉写得非常好，于是打算总结下这方面的工作，作者将BEV Perception算法做如下分类：

算法的核心是如何将PV图上的Feature投影到BEV上，投影的方法分为Homograph Based，Depth Based，MLP Based，Transformer Based四类，每一类都有许多具体的算法，如下：
Homograph Based：

Depth Based：

MLP Based：

Transformer Based:

因为精力有限，我很难将所有的的算法都看一遍，我将从每个类别中挑出一到两种我个人认为比较有代表性的方法进行总结分析，主要结合代码具体解读下图像特征投影到BEV下的这一过程。

1. Homograph Based——3D LaneNet

3D LaneNet发表于2018年，论文名为《3D-LaneNet: End-to-End 3D Multiple Lane Detection》，该算法会通过网络显示地估计一个单应矩阵，并通过该矩阵将前视图的特征投影到BEV上，然后再基于Anchor检测车道线。

算法估计的单应矩阵的定义是这样的，首先，需要相机和和路面进行如下建模：

相机坐标系为${\mathcal{C}}_{\text{camera }}=\left(\dot{x},\dot{y},\dot{z}\right)$，其中$\dot{y}$为相机观察方向，路面坐标系为${\mathcal{C}}_{\text{road }}=(x,y,z)$，其中$z$为路面法向，$y$是$\dot{y}$在路面上的投影方向。$T_{c2r}$为相机坐标系到路面坐标系的3D变换，在3D LaneNet中，算法假设相机相对路面的Roll角为零，那么$T_{c2r}$仅仅取决于相机的Pitch角$\theta$和高度$h_{cam}$，而从相机成像平面到路面平面的单应矩阵$H_{r2i}$就由$T_{c2r}$和相机内参$\kappa$决定，这一部分不熟悉的同学可以参看多视图几何总结——基础矩阵、本质矩阵和单应矩阵的自由度分析。最后根据单应矩阵$H_{r2i}$就可以构建一个通过采样获得的投影栅格$S_{IPM}$，逐个像素的映射关系就通过该栅格进行双线性采样获得。

该论文的网络结构如下图所示：

整个网络结构由Road Projection Prediction Branch（上半部分）和Lane Prediction Head（下半部分）构成，其中Road Projection Prediction Branch负责预测相机相对于路面的的Pitch角$\theta$和高度$h_{cam}$，构建出用于投影的栅格$S_{IPM}$，将前视图提取的Feature映射到BEV上。Lane Prediction Head则在BEV构建Anchor进行车道线检测，车道线检测部分不展开，其实我很想看下Projection to Top是怎么实现的，但是没有找到相关的源码就没法做进一步的学习了。

2. Depth Based——LSS

LSS发表于2020年，原论文名为《Lift, Splat, Shoot: Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D》，该算法会通过网络显示地估计图像的深度信息，通过该深度信息将前视图特征投影到BEV上，并基于BEV特征进行语义分割。

原论文中没有网络结构图，我们可以参考下另外BEVDet这篇论文中的网络结构图：

通过LSS论文名我们也可以看出，该算法主要分为三部分，其中Lift指的是从每个图像生成特征视锥过程，Splat指的是将特征视锥栅格化到BEV的过程，而Shoot是基于BEV特征进行运动规划。我们这里主要来结合代码看下前两部分具体是如实现的。

在代码中，模型主要由两部分组成，

def forward(self, x, rots, trans, intrins, post_rots, post_trans):
    x = self.get_voxels(x, rots, trans, intrins, post_rots, post_trans)
    x = self.bevencode(x)
    return x

其中，get_voxel即包含Lift和Splat的过程，而bevencode则是通过Resnet对BEV特征进行进一步Encode。

def get_voxels(self, x, rots, trans, intrins, post_rots, post_trans):
    geom = self.get_geometry(rots, trans, intrins, post_rots, post_trans)
    x = self.get_cam_feats(x)

    x = self.voxel_pooling(geom, x)

    return x

其中，get_geometry是通过相机的内外参生成一个从图像系到车体系的视锥映射表，get_cam_feats则是获取图像特征以及深度，voxel_pooling则是将图像特征利用get_geometry生成的映射表变换成视锥特征并栅格化。

下面我们先来看下get_geometry的具体实现，要获得从图像系到车体系的视锥映射表就要先获得从图像系到相机系的映射表，在代码中用self.frustum这个变量表示，这个变量是通过create_frustum这个函数生成的：

def create_frustum():
    # 原始图片大小  ogfH:128  ogfW:352
    ogfH, ogfW = self.data_aug_conf['final_dim']
    
    # 下采样16倍后图像大小  fH: 8  fW: 22
    fH, fW = ogfH // self.downsample, ogfW // self.downsample 
     
    # self.grid_conf['dbound'] = [4, 45, 1]
    # 在深度方向上划分网格 ds: DxfHxfW (41x8x22)
    ds = torch.arange(*self.grid_conf['dbound'], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)
    
    # D: 41 表示深度方向上网格的数量
    D, _, _ = ds.shape 
    
    # 在0到351上划分22个格子 xs: DxfHxfW(41x8x22)
    xs = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(1, 1, fW).expand(D, fH, fW)  
    
    # 在0到127上划分8个格子 ys: DxfHxfW(41x8x22)
    ys = torch.linspace(0, ogfH - 1, fH, dtype=torch.float).view(1, fH, 1).expand(D, fH, fW)  
    
    # D x H x W x 3
    # 堆积起来形成网格坐标, frustum[i,j,k,0]就是(i,j)位置，深度为k的像素的宽度方向上的栅格坐标   frustum: DxfHxfWx3
    frustum = torch.stack((xs, ys, ds), -1)  
    return nn.Parameter(frustum, requires_grad=False)

可以看到frustum是由图像栅格坐标集xs, ys和离散深度坐标集ds通过stack构造的，其含义是覆盖整个预设区域的等间隔的点集，frustum[i,j,k,0]就是(i,j)位置，深度为k的像素的宽度方向上的栅格坐标，类推frustum[i,j,k,1]，frustum[i,j,k,2]分别就是高度和深度方向上的栅格坐标，当然整个坐标目前还是在图像坐标系下，但是当我们对这个点集进行内外参变化后，就可以得到相机系下的栅格坐标到车体系下的栅格坐标的映射，这也就可以使得我们可以通过查坐标的方式快速地将图像系下的特征投影到车体系下，这正是get_geometry做的事情。

get_geometry涉及到的坐标变换其实很简单，可以参考如下公式：$$\lambda \left(\begin{array}{l}x\\ y\\ 1\end{array}\right)=\left[\mathbf{K}\mid 0_3\right]\left[\begin{array}{cc}\mathbf{R}& -\mathbf{R}\mathbf{t}\\ 0_3^T& 1\end{array}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)$$从右到左可以是看作是从车体下到相机系的投影过程，其中$\mathbf{K}$是内参矩阵，$\mathbf{R}$和$\mathbf{t}$是外参的旋转和平移，get_geometry的操作其实就是反过来从左到右进行计算，代码中第一步就是将网络估计出来的$\lambda$和图像系坐标$x$和$y$相乘得到归一化相机坐标系坐标，第二步则是将内外参矩阵的逆乘到归一化相机坐标系坐标得到车体系坐标，如下：

def get_geometry(self, rots, trans, intrins, post_rots, post_trans):
    """Determine the (x,y,z) locations (in the ego frame)
    of the points in the point cloud.
    Returns B x N x D x H/downsample x W/downsample x 3
    """
    B, N, _ = trans.shape

    # undo post-transformation
    # B x N x D x H x W x 3
    points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3)
    points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1))

    # cam_to_ego
    # 第一步
    points = torch.cat((points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
                        points[:, :, :, :, :, 2:3]
                        ), 5)
    # 第二步
    combine = rots.matmul(torch.inverse(intrins))
    points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
    points += trans.view(B, N, 1, 1, 1, 3)

    return points

下面我们来看下get_cam_feats的代码，其主要作用就是提取前视图特征：

def get_cam_feats(self, x):
    """Return B x N x D x H/downsample x W/downsample x C
    """
    B, N, C, imH, imW = x.shape

    x = x.view(B*N, C, imH, imW)
    x = self.camencode(x)
    x = x.view(B, N, self.camC, self.D, imH//self.downsample, imW//self.downsample)
    x = x.permute(0, 1, 3, 4, 5, 2)

    return x

代码中camencode中最核心的代码是：

def get_depth_feat(self, x):
    x = self.get_eff_depth(x)
    # Depth
    x = self.depthnet(x)

    depth = self.get_depth_dist(x[:, :self.D])
    new_x = depth.unsqueeze(1) * x[:, self.D:(self.D + self.C)].unsqueeze(2)

    return depth, new_x

前视图特征提取部分是使用的EfficientNet作为backbone，将最后两层的特征输出concate到一起后通过一个卷积输出为$D+C$个通道的特征x，其中$D$用于预测深度，$C$用于预测图像特征，并最终会将图像特征和预测深度做点积获得$D\times C$的特征，如下图所示：

这样相当于每个像素的每一个离散深度上都会有一个特征，该特征和估计的深度分布以及图像特征有关，也就是上述代码中的new_x，不同相机的new_x在后续就会通过先验的frustum映射和pooling操作在BEV下进行融合。

最后就是voxel_pooling的代码：

def voxel_pooling(self, geom_feats, x):
    # geom_feats；(B x N x D x H x W x 3)：在ego坐标系下的坐标点；
    # x；(B x N x D x fH x fW x C)：图像点云特征

    B, N, D, H, W, C = x.shape
    Nprime = B*N*D*H*W 

    # 将特征点云展平，一共有 B*N*D*H*W 个点
    x = x.reshape(Nprime, C) 

    # flatten indices
    # ego下的空间坐标转换到体素坐标（计算栅格坐标并取整），并将体素坐标同样展平，并记录每个点对应于哪个batch
    geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long()
    geom_feats = geom_feats.view(Nprime, 3)  # geom_feats: (B*N*D*H*W, 3)
    batch_ix = torch.cat([torch.full([Nprime//B, 1], ix,
                             device=x.device, dtype=torch.long) for ix in range(B)])  
    geom_feats = torch.cat((geom_feats, batch_ix), 1)  # geom_feats: (B*N*D*H*W, 4)

    # filter out points that are outside box
    # 过滤掉在边界线之外的点 x:0~199  y: 0~199  z: 0
    kept = (geom_feats[:, 0] >= 0) & (geom_feats[:, 0] < self.nx[0])\
        & (geom_feats[:, 1] >= 0) & (geom_feats[:, 1] < self.nx[1])\
        & (geom_feats[:, 2] >= 0) & (geom_feats[:, 2] < self.nx[2])
    x = x[kept]
    geom_feats = geom_feats[kept]

    # get tensors from the same voxel next to each other
    # 给每一个点计算一个rank值，rank相等的点在同一个batch，并且在在同一个格子里面，geam_feats的0，1，2，3分别是车体系下x,y,z,batch_id
    ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)\
         + geom_feats[:, 1] * (self.nx[2] * B)\
         + geom_feats[:, 2] * B\
         + geom_feats[:, 3]
    sorts = ranks.argsort()
    x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts]
   
    # cumsum trick
    # 对处于同一个BEV栅格中的特征进行求和
    if not self.use_quickcumsum:
        x, geom_feats = cumsum_trick(x, geom_feats, ranks)
    else:
        x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks)

    # griddify (B x C x Z x X x Y)
    # 将x按照栅格坐标放到final中
    final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device)  # final: bs x 64 x 1 x 200 x 200
    final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x 

    # collapse Z
    final = torch.cat(final.unbind(dim=2), 1)

    return final  # final: bs x 64 x 200 x 200

其中，必要容易忽略的一步是最后会将所有z方向的特征concate到一起，通道数会变得比较大，除此之外另一个比较有意思的部分是QuickCumsum部分，代码如下：

class QuickCumsum(torch.autograd.Function):
    @staticmethod
    def forward(ctx, x, geom_feats, ranks):
        x = x.cumsum(0) # 求前缀和
        kept = torch.ones(x.shape[0], device=x.device, dtype=torch.bool)  
        kept[:-1] = (ranks[1:] != ranks[:-1])  # 筛选出ranks中前后rank值不相等的位置

        x, geom_feats = x[kept], geom_feats[kept]  # rank值相等的点只留下最后一个，即一个batch中的一个格子里只留最后一个点
        x = torch.cat((x[:1], x[1:] - x[:-1]))  # x后一个减前一个，还原到cumsum之前的x，此时的一个点是之前与其rank相等的点的feature的和，相当于把同一个格子的点特征进行了sum

        # save kept for backward
        ctx.save_for_backward(kept)

        # no gradient for geom_feats
        ctx.mark_non_differentiable(geom_feats)

        return x, geom_feats

这种方法叫做Frustum Pooling，将$N$个图像产生的视锥特征转化为与图像数量无关的维度为$C\times N\times W$的张量。下面是结合网上的一个例子和源码的对QuickCumsum函数的流程图：

如果所示，可以看到输出的x正好是rank相同的位置求和的结果。网上看到有个同学问题，完成Frustum Pooling的一个前提是要进行排序，而排序的时间复杂度是要高于for循环的，问为什么要这么做？我的个人理解是for循环在Python实现中是非常慢的，排序后Frustum Pooling的操作都可以通过numpy完成，因此速度反而更快。以上就完成了从基于Depth的从前视图到BEV的投影过程。

3. MLP Based——PON

PON发表于2020年，原论文名为《Predicting Semantic Map Representations from Images using Pyramid Occupancy Networks》，该算法通过MLP隐式地将图像信息映射到BEV上，再在BEV上进行分割。

网络结构如下图所示：

从网络结构图我们可以看出来，算法主要分为四个部分，整个模型代码在pyramid.py中，由四部分构成：

def forward(self, image, calib, *args):

    # Extract multiscale feature maps
    feature_maps = self.frontend(image)

    # Transform image features to birds-eye-view
    bev_feats = self.transformer(feature_maps, calib)

    # Apply topdown network
    td_feats = self.topdown(bev_feats)

    # Predict individual class log-probabilities
    logits = self.classifier(td_feats)
    return logits

这里我们着重介绍将特征从图像坐标系转换到BEV坐标系的Transformer的部分，代码如下：

class DenseTransformer(nn.Module):

    def __init__(self, in_channels, channels, resolution, grid_extents, 
                 ymin, ymax, focal_length, groups=1):
        super().__init__()

        # Initial convolution to reduce feature dimensions
        self.conv = nn.Conv2d(in_channels, channels, 1)
        self.bn = nn.GroupNorm(16, channels)

        # Resampler transforms perspective features to BEV
        self.resampler = Resampler(resolution, grid_extents)

        # Compute input height based on region of image covered by grid
        self.zmin, zmax = grid_extents[1], grid_extents[3]
        self.in_height = math.ceil(focal_length * (ymax - ymin) / self.zmin)
        self.ymid = (ymin + ymax) / 2

        # Compute number of output cells required
        self.out_depth = math.ceil((zmax - self.zmin) / resolution)

        # Dense layer which maps UV features to UZ
        self.fc = nn.Conv1d(
            channels * self.in_height, channels * self.out_depth, 1, groups=groups
        )
        self.out_channels = channels
    

    def forward(self, features, calib, *args):

        # Crop feature maps to a fixed input height
        features = torch.stack([self._crop_feature_map(fmap, cal) 
                                for fmap, cal in zip(features, calib)])
        
        # Reduce feature dimension to minimize memory usage
        features = F.relu(self.bn(self.conv(features)))

        # Flatten height and channel dimensions
        B, C, _, W = features.shape
        flat_feats = features.flatten(1, 2)
        bev_feats = self.fc(flat_feats).view(B, C, -1, W)

        # Resample to orthographic grid
        return self.resampler(bev_feats, calib)


    def _crop_feature_map(self, fmap, calib):
        
        # Compute upper and lower bounds of visible region
        focal_length, img_offset = calib[1, 1:]
        vmid = self.ymid * focal_length / self.zmin + img_offset
        vmin = math.floor(vmid - self.in_height / 2)
        vmax = math.floor(vmid + self.in_height / 2)

        # Pad or crop input tensor to match dimensions
        return F.pad(fmap, [0, 0, -vmin, vmax - fmap.shape[-2]])

其中最关键的步骤就是通过一个nn.Conv1d将PV的特征图映射到BEV下，经过这一步在BEV下的Feature的大小是$B\times C\times H\times W$的一个矩阵特征，但实际上，PV的特征图投影到BEV下应该是一个Frustrum，因此，在映射完成后还需要根据内外参进行一次Resample，Resample的操作如下：

class Resampler(nn.Module):

    def __init__(self, resolution, extents):
        super().__init__()

        # Store z positions of the near and far planes
        self.near = extents[1]
        self.far = extents[3]

        # Make a grid in the x-z plane
        self.grid = _make_grid(resolution, extents)


    def forward(self, features, calib):

        # Copy grid to the correct device
        self.grid = self.grid.to(features)
        
        # We ignore the image v-coordinate, and assume the world Y-coordinate
        # is zero, so we only need a 2x2 submatrix of the original 3x3 matrix
        calib = calib[:, [0, 2]][..., [0, 2]].view(-1, 1, 1, 2, 2)

        # Transform grid center locations into image u-coordinates
        cam_coords = torch.matmul(calib, self.grid.unsqueeze(-1)).squeeze(-1)

        # Apply perspective projection and normalize
        ucoords = cam_coords[..., 0] / cam_coords[..., 1]
        ucoords = ucoords / features.size(-1) * 2 - 1

        # Normalize z coordinates
        zcoords = (cam_coords[..., 1]-self.near) / (self.far-self.near) * 2 - 1

        # Resample 3D feature map
        grid_coords = torch.stack([ucoords, zcoords], -1).clamp(-1.1, 1.1)
        return F.grid_sample(features, grid_coords)


def _make_grid(resolution, extents):
    # Create a grid of cooridinates in the birds-eye-view
    x1, z1, x2, z2 = extents
    zz, xx = torch.meshgrid(
        torch.arange(z1, z2, resolution), torch.arange(x1, x2, resolution))

    return torch.stack([xx, zz], dim=-1)

在上述代码中XYZ坐标系指的是相机坐标系，uv坐标系指的是图像坐标系，代码中给定的内参矩阵的计算如下：$$\lambda \left(\begin{array}{l}u\\ 1\end{array}\right)=\left[\begin{array}{cc}{f}_x& c_x\\ 0& 1\end{array}\right]\left(\begin{array}{c}X\\ Z\end{array}\right)$$因此最后计算出来的ucoords为u方向坐标$f_x\frac{X}{Z}+c_x$和图像宽度的比值，而zcoords则为深度$\lambda$和深度范围的比值，最后通过F.grid_sample对BEV下的特征图进行采样。F.grid_sample的用法可以参考PyTorch中grid_sample的使用方法。以上就完成了通过MLP将PV特征投影到BEV的全过程。

4. Transformer Based——BEVFormer

BEVFormer发表于2022年ECCV，该论文的方法和2021年Tesla AI Day上介绍的方案非常相似，主要通过Transformer将BEV和PV上的Feature进行关联。基于Transformer的的方法在BEVFormer之前类似的方法有DETR 3D，DETR 3D和原始的DETR方法比较接近，每个Query代表一个检测目标，这些Query是稀疏的，具体可以参考计算机视觉算法——基于Transformer的目标检测（DETR / Deformable DETR / DETR 3D），而BEVFormer则利用稠密的Query提取了一个稠密的BEV Feature，使得网络可以方便的进行时序融合以及兼容分割任务，BEVFormer的网络结构如下：

如上图所示，这里我们不对Temporal Self-Attention（时序融合部分）深入展开，主要看下Spatial Cross-Attention（特征投影部分）的实现方式：
首先如上图所示，Spatial Cross Attention会首先在BEV上初始化一系列带有位置先验信息的Query，然后再将这些Query的分布到不同的高度上，从代码上看同一位置不同高度的Query是相同的，

# ref_3d 坐标生成
zs = torch.linspace(0.5, Z - 0.5, num_points_in_pillar, dtype=dtype, device=device).view(-1, 1, 1).expand(num_points_in_pillar, H, W) / Z
xs = torch.linspace(0.5, W - 0.5, W, dtype=dtype, device=device).view(1, 1, W).expand(num_points_in_pillar, H, W) / W
ys = torch.linspace(0.5, H - 0.5, H, dtype=dtype, device=device).view(1, H, 1).expand(num_points_in_pillar, H, W) / H
ref_3d = torch.stack((xs, ys, zs), -1)  # (4, 200, 200, 3)  (level, bev_h, bev_w, 3) 3代表 x,y,z 坐标值
ref_3d = ref_3d.permute(0, 3, 1, 2).flatten(2).permute(0, 2, 1)  # (4, 200 * 200, 3)
ref_3d = ref_3d[None].repeat(bs, 1, 1, 1)  # (1, 4, 200 * 200, 3)

# (level, bs, cam, num_query, 4)
reference_points_cam = torch.matmul(lidar2img.to(torch.float32), reference_points.to(torch.float32)).squeeze(-1)
eps = 1e-5
bev_mask = (reference_points_cam[..., 2:3] > eps)  # (level, bs, cam, num_query, 1)
reference_points_cam = reference_points_cam[..., 0:2] / torch.maximum(reference_points_cam[..., 2:3], torch.ones_like(reference_points_cam[..., 2:3]) * eps)

# reference_points_cam = (bs, cam = 6, 40000, level = 4, xy = 2)
reference_points_cam[..., 0] /= img_metas[0]['img_shape'][0][1]  # 坐标归一化
reference_points_cam[..., 1] /= img_metas[0]['img_shape'][0][0]

# bev_mask 用于评判某三维坐标点 是否落在了二维坐标平面上
# bev_mask = (bs, cam = 6, 40000, level = 4)
bev_mask = (bev_mask & (reference_points_cam[..., 1:2] > 0.0)
                     & (reference_points_cam[..., 1:2] < 1.0)
                     & (reference_points_cam[..., 0:1] < 1.0)
                     & (reference_points_cam[..., 0:1] > 0.0))

其中lidar2img矩阵就是BEV坐标系到图像系的变换矩阵，这里想提及的两点是：（1）在DETR 3D中参考点的坐标是在Query的基础上通过MLP生成的，而BEV Former的Reference Point位置和Query本身的值无关；（2）从3D到2D的投影过程中是用到了标定的内外参的，在后序的一些工作中，有尝试将这部分也通过网络进行学习，例如BEVSegFormer等。我们可以想到，如果将上述所有的BEV Query投影到各个相机上进行Cross Attention计算量会非常大，因此代码中这里计算了各个相机投影覆盖的bev_mask，然后利用bev_mask去除无效BEV Query以减小计算量，如下：

indexes = []
# 根据每张图片对应的`bev_mask`结果，获取有效query的index
for i, mask_per_img in enumerate(bev_mask):
    index_query_per_img = mask_per_img[0].sum(-1).nonzero().squeeze(-1)
    indexes.append(index_query_per_img)

queries_rebatch = query.new_zeros([bs * self.num_cams, max_len, self.embed_dims])
reference_points_rebatch = reference_points_cam.new_zeros([bs * self.num_cams, max_len, D, 2]) 

for i, reference_points_per_img in enumerate(reference_points_cam):
    for j in range(bs):
        index_query_per_img = indexes[i]

        # 重新整合 `bev_query` 特征，记作 `query_rebatch
        queries_rebatch[j * self.num_cams + i, :len(index_query_per_img)] = query[j, index_query_per_img]

        # 重新整合 `reference_point`采样位置，记作`reference_points_rebatch`
        reference_points_rebatch[j * self.num_cams + i, :len(index_query_per_img)] = reference_points_per_img[j, index_query_per_img]

然后根据重整后的query_rebatch和reference_points_rebatch计算Weight和Offset，在Deformable Transformer中，Weight和Offset都是基于Query通过线性层直接获得的，在Cross Attention的过程中逐渐更新Query进而更新Weight和Offset，这部分代码如下：

 # sample 8 points for single ref point in each level.

# sampling_offsets: shape = (bs, max_len, 8, 4, 8, 2)
sampling_offsets = self.sampling_offsets(query).view(bs, num_query, self.num_heads, self.num_levels, self.num_points, 2)
attention_weights = self.attention_weights(query).view(bs, num_query, self.num_heads, self.num_levels * self.num_points)

attention_weights = attention_weights.softmax(-1)

# attention_weights: shape = (bs, max_len, 8, 4, 8)
attention_weights = attention_weights.view(bs, num_query,
                                           self.num_heads,
                                           self.num_levels,
                                           self.num_points)

offset_normalizer = torch.stack([spatial_shapes[..., 1], spatial_shapes[..., 0]], -1)

reference_points = reference_points[:, :, None, None, None, :, :]
sampling_offsets = sampling_offsets / offset_normalizer[None, None, None, :, None, :]
sampling_locations = reference_points + sampling_offsets

最后就是将sample_location以attention_weights送入封装好的Deformable Attention模块中与图像的特征value进行Cross Attention，最后得到的Attention值在BEV下求平均就得到下一轮的BEV Query：

output = MultiScaleDeformableAttnFunction.apply(value, spatial_shapes, level_start_index, sampling_locations,
                attention_weights, self.im2col_step)

for i, index_query_per_img in enumerate(indexes):
    for j in range(bs):  # slots: (bs, 40000, 256)
        slots[j, index_query_per_img] += queries[j * self.num_cams + i, :len(index_query_per_img)]

count = bev_mask.sum(-1) > 0
count = count.permute(1, 2, 0).sum(-1)
count = torch.clamp(count, min=1.0)
slots = slots / count[..., None]  # maybe normalize.
slots = self.output_proj(slots)

以上操作重复六次后最后得到的BEV Query就是对外输出的BEV Feature。以上就是将图像Feature通过Transformer投影到BEV的基本逻辑。在BEV Former的论文中正好对LSS和VPN算法（和PON同类型）进行了对比，结果如下：

可以看到，BEV Former的计算量相对会更大，在论文中有介绍在V100上BEV Former的FPS只能到1~2Hz左右。除此之外，2023年的BEV Former又出了一个V2的版本，投影的基本思路不变，主要的优化点是增加了PV的监督，并将一阶段PV的Proposal补充作为二阶段BEV检测的Query，从而使得性能进一步提升，具体可以直接看论文《BEVFormer v2: Adapting Modern Image Backbones to Bird’s-Eye-View Recognition via Perspective Supervision》

5. Transformer Based——Translating Image into Maps

Translating Image into Maps是CVPR 2022的Best Paper，这篇Paper同样是基于Transformer实现的，但是其思路和BEV Former却完全不同，更像是PON的升级版，PON是通过MLP将PV的Feature映射到BEV上然后再进行采样，而本方法则是将MLP更换为了Transfomer的Encoder和Decoder，下面是该方法的网络结构：

这里我们先看下论文中对该方法的描述，如上图所示，投影过程分为Inter-plane Attention和Polar Ray Self-attention，所谓Inter-plane Attention指的是将图像特征按列划分进行输入Transformer Encoder进行Self Attention后得到$\mathbf{h}\in {\mathbb{R}}^{H\times C}$，然后将其和大小为$\mathbf{y}\in {\mathbb{R}}^{r\times C}$的Query送入Transformer Decoder进行Cross Attention，其中$r$为每个polay ray的深度。我们知道，为了使得最后的结果具备全局信息，在Transformer Decoder的每层Cross Attention中通常会带有Self Attention，这个就被定义为Polay Ray Self-attention。

经过上述Transfomer Encoder-Decoder，得到的就是类似于PON中MLP处理后的一个BEV Feature，然后经过基于内外参生成的Grid采样后就可以得到最后的BEV Feature。在源码中实现的模型架构非常多，如下是PyrOccTranDetr_S_0904_old_rep100x100_out100x100版本的前向推理部分：

def forward(self, image, calib, grid):
    N = image.shape[0]
    # Normalize by mean and std-dev
    image = (image - self.mean.view(3, 1, 1)) / self.std.view(3, 1, 1)

    # Frontend outputs
    feats = self.frontend(image)

    # Crop feature maps to certain height
    feat8 = feats["0"][:, :, self.h_start[0] : self.h_end[0], :]
    feat16 = feats["1"][:, :, self.h_start[1] : self.h_end[1], :]
    feat32 = feats["2"][:, :, self.h_start[2] : self.h_end[2], :]
    feat64 = feats["3"][:, :, self.h_start[3] : self.h_end[3], :]

    # Apply Transformer
    tgt8 = torch.zeros_like(feat8[:, 0, :1]).expand(
        -1, self.z_idx[-1] - self.z_idx[-2], -1
    )
    tgt16 = torch.zeros_like(feat16[:, 0, :1]).expand(
        -1, self.z_idx[-2] - self.z_idx[-3], -1
    )
    tgt32 = torch.zeros_like(feat32[:, 0, :1]).expand(
        -1, self.z_idx[-3] - self.z_idx[-4], -1
    )
    tgt64 = torch.zeros_like(feat64[:, 0, :1]).expand(-1, self.z_idx[-4], -1)

    qe8 = (self.query_embed(tgt8.long())).permute(0, 3, 1, 2)
    qe16 = (self.query_embed(tgt16.long())).permute(0, 3, 1, 2)
    qe32 = (self.query_embed(tgt32.long())).permute(0, 3, 1, 2)
    qe64 = (self.query_embed(tgt64.long())).permute(0, 3, 1, 2)

    tgt8 = (tgt8.unsqueeze(-1)).permute(0, 3, 1, 2)
    tgt16 = (tgt16.unsqueeze(-1)).permute(0, 3, 1, 2)
    tgt32 = (tgt32.unsqueeze(-1)).permute(0, 3, 1, 2)
    tgt64 = (tgt64.unsqueeze(-1)).permute(0, 3, 1, 2)

    bev8 = checkpoint(
        self.tbev8,
        self.trans_reshape(feat8),
        self.pos_enc(self.trans_reshape(tgt8)),
        self.trans_reshape(qe8),
        self.pos_enc(self.trans_reshape(feat8)),
    )
    bev16 = checkpoint(
        self.tbev16,
        self.trans_reshape(feat16),
        self.pos_enc(self.trans_reshape(tgt16)),
        self.trans_reshape(qe16),
        self.pos_enc(self.trans_reshape(feat16)),
    )
    bev32 = checkpoint(
        self.tbev32,
        self.trans_reshape(feat32),
        self.pos_enc(self.trans_reshape(tgt32)),
        self.trans_reshape(qe32),
        self.pos_enc(self.trans_reshape(feat32)),
    )
    bev64 = checkpoint(
        self.tbev64,
        self.trans_reshape(feat64),
        self.pos_enc(self.trans_reshape(tgt64)),
        self.trans_reshape(qe64),
        self.pos_enc(self.trans_reshape(feat64)),
    )

    # Resample polar BEV to Cartesian
    bev8 = self.sample8(self.bev_reshape(bev8, N), calib, grid[:, self.z_idx[2] :])
    bev16 = self.sample16(
        self.bev_reshape(bev16, N), calib, grid[:, self.z_idx[1] : self.z_idx[2]]
    )
    bev32 = self.sample32(
        self.bev_reshape(bev32, N), calib, grid[:, self.z_idx[0] : self.z_idx[1]]
    )
    bev64 = self.sample64(
        self.bev_reshape(bev64, N), calib, grid[:, : self.z_idx[0]]
    )

    bev = torch.cat([bev64, bev32, bev16, bev8], dim=2)

    # Apply DLA on topdown
    down_s1 = checkpoint(self.topdown_down_s1, bev)
    down_s2 = checkpoint(self.topdown_down_s2, down_s1)
    down_s4 = checkpoint(self.topdown_down_s4, down_s2)
    down_s8 = checkpoint(self.topdown_down_s8, down_s4)

    node_1_s1 = checkpoint(
        self.node_1_s1,
        torch.cat([self.id_node_1_s1(down_s1), self.up_node_1_s1(down_s2)], dim=1),
    )
    node_2_s2 = checkpoint(
        self.node_2_s2,
        torch.cat([self.id_node_2_s2(down_s2), self.up_node_2_s2(down_s4)], dim=1),
    )
    node_2_s1 = checkpoint(
        self.node_2_s1,
        torch.cat(
            [self.id_node_2_s1(node_1_s1), self.up_node_2_s1(node_2_s2)], dim=1
        ),
    )
    node_3_s4 = checkpoint(
        self.node_3_s4,
        torch.cat([self.id_node_3_s4(down_s4), self.up_node_3_s4(down_s8)], dim=1),
    )
    node_3_s2 = checkpoint(
        self.node_3_s2,
        torch.cat(
            [self.id_node_3_s2(node_2_s2), self.up_node_3_s2(node_3_s4)], dim=1
        ),
    )
    node_3_s1 = checkpoint(
        self.node_3_s1,
        torch.cat(
            [self.id_node_3_s1(node_2_s1), self.up_node_3_s1(node_3_s2)], dim=1
        ),
    )

    # Predict encoded outputs
    batch, _, depth_s8, width_s8 = down_s8.size()
    _, _, depth_s4, width_s4 = node_3_s4.size()
    _, _, depth_s2, width_s2 = node_3_s2.size()
    _, _, depth_s1, width_s1 = node_3_s1.size()
    output_s8 = self.head_s8(down_s8).view(batch, -1, 1, depth_s8, width_s8)
    output_s4 = self.head_s4(node_3_s4).view(batch, -1, 1, depth_s4, width_s4)
    output_s2 = self.head_s2(node_3_s2).view(batch, -1, 1, depth_s2, width_s2)
    output_s1 = self.head_s1(node_3_s1).view(batch, -1, 1, depth_s1, width_s1)

    return (
        output_s1.squeeze(2),
        output_s2.squeeze(2),
        output_s4.squeeze(2),
        output_s8.squeeze(2),
    )

其中tbev8、tbev16、tbev32、tbev64即不同分辨率下的Transfomer投影函数，sample完成后最后是通过DLA的Backbone在BEV Feature进行进一步特征提取。

在论文中除了提出了这种基于列的Transformer投影方式，还进一步讨论了Monotonic Attention机制，大概含义是指通过Monotonic Attention可以更好的利用图像中越上越远这种先验，具体实现就是将上述Transfomer模块更换为TransofemerMA模块，这里比较细节就不进一步展开，感兴趣的同学可以打开代码再学习下。

以上就完成了目前主流的几种BEV投影方式的原理分析和代码解读，目前工业上用得比较多的还是PON和LSS的方法，BEV Former的方法受限于计算量和Deformable Attention算子化实现，Translating Image into Maps的方法论文效果很好但目前还没有看到太多相关的讨论，有了解原因的读者欢迎补充~