文章目录
- 【`获取资源`请见文章第5节:资源获取】
- 1. 原始COA算法
- 1.1 开发阶段
- 1.2 探索阶段
- 2. 改进后的ICOA算法
- 2.1 Circle映射种群初始化
- 2.2 Levy飞行策略
- 2.3 透镜成像折射反向学习策略
- 3. 部分代码展示
- 4. 仿真结果展示
- 5. 资源获取
【获取资源请见文章第5节:资源获取】
1. 原始COA算法
长鼻浣熊优化算法(Cоati Optimization Algorithm,COA)是一种启发式优化算法,灵感来源于长鼻浣熊(Coati)的行为策略。长鼻浣熊优化算法基于长鼻浣熊在觅食过程中的特性和行为模式。长鼻浣熊是一种树栖动物,具有长而灵活的鼻子,用于觅食和捕食。它们通过嗅觉感知周围环境,利用敏锐的视觉和协调的运动能力来寻找食物。
1.1 开发阶段
这个阶段模拟的是浣熊对鬣蜥的攻击策略,对搜索空间中的种群更新的第一个阶段进行建模。在这个策略中,一群浣熊会爬上树,对着一只鬣蜥,并吓唬它,其他几个浣熊会在树下等待鬣蜥掉下来。当鬣蜥掉下来之后,浣熊就会攻击并猎杀它。这个策略使得COA在搜索空间中移动到不同的位置,说明COA在问题解决空间中的全局搜索能力。
在COA的设计中,种群中的最佳位置被假定为鬣蜥的位置。此外,还假设有一般的浣熊能爬上树,另一半在地上等待鬣蜥掉下来。因此,浣熊在树上的位置可以用以下公式描述:

鬣蜥落地后,将其放置在搜索空间中的任意位置。基于这种随机位置,地面上的浣熊可以在搜索空间中移动,用下列公式来描述:

对于每个浣熊计算的新位置,如果它改善了目标函数的值,那么就会被接受,否则,浣熊将保持原先的位置,此过程用以下公式来表示。这个可以被视为贪婪法则。

这里
x
i
P
1
x_{i}^{P1}
xiP1是计算第
i
i
i个浣熊的新位置,
x
i
,
j
P
1
x_{i,j}^{P1}
xi,jP1是它的第
j
j
j维,
F
i
P
1
F_{i}^{P1}
FiP1是它的目标函数值,
r
r
r是
[
0
,
1
]
[0,1]
[0,1]区间内的随机实数。
I
g
u
a
n
a
Iguana
Iguana代表鬣蜥在搜索空间中的位置,这实际上是指种群中最佳个体的位置;
I
g
u
a
n
a
j
Iguana_{j}
Iguanaj是它的第
j
j
j维,
j
j
j是一个整数,从集合{1,2}中随机选择,
I
g
u
a
n
a
G
Iguana^{G}
IguanaG是在地面上的位置,它是随机生成的。
I
g
u
a
n
a
j
G
Iguana_{j}^{G}
IguanajG蠢晰是它的第
j
j
j维,
F
I
g
u
a
n
a
G
F_{Iguana}^{G}
FIguanaG是它的目标函数值。
1.2 探索阶段
在第二阶段即探索阶段的过程中,位置更新模拟的是浣熊在遇到捕食者和逃避捕食者的行为。当食肉动物攻击浣熊时,浣熊就会从它的位置上逃走。浣熊在该策略中的移动使其处于接近其当前位置的安全位置,这代表这COA的局部开发能力。为了模拟这种行为,COA在每个长鼻浣熊个体附近生成一个随机位置,公式如下所示:

与开发阶段中类似,同样使用贪婪选择来决定是替换还是保留原先的位置。
2. 改进后的ICOA算法
2.1 Circle映射种群初始化
Circle混沌映射在混沌理论研究、密码学、随机数生成和通信系统中具有一定的应用。它展示了非线性系统中的复杂动力学行为,并且可以用来生成具有高度随机性的序列。
Circle的公式如下:

2.2 Levy飞行策略
在COA浣熊开发阶段的位置更新公式中,会根据目前的个体最优值来更新自己的位置,也容易陷入局部最优,此时可以使用莱维飞行策略进行位置更新使得这部分个体去到更广的搜索空间:

2.3 透镜成像折射反向学习策略
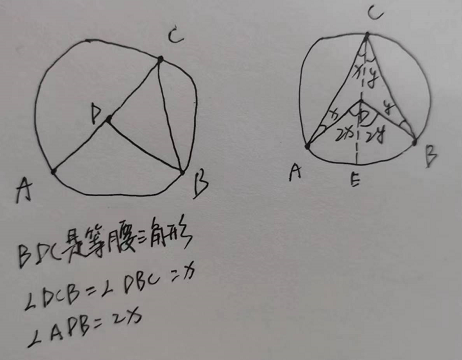
透镜成像折射反向学习策略的思想来自于凸透镜成像的原理。通过基于当前坐标生成一个反向位置来扩展搜索范围,如图1所示。

在二维坐标中,x轴的搜索范围为(a, b), y轴表示一个凸透镜。假设物体A在x轴上的投影为x,高度为h,通过透镜成像,另一侧的图像为A*, A在x轴上的投影为x,高度为h*。通过以上分析,我们可以得到如下公式:
(
a
+
b
)
/
2
−
x
x
∗
−
(
a
+
b
)
/
2
=
h
h
∗
(1)
\frac{(a+b)/2-x}{x^{*}-(a+b)/2 }=\frac{h}{h^{*}} \tag1
x∗−(a+b)/2(a+b)/2−x=h∗h(1)
对公式(1)进行转换,即可得到反向解x*的表达式为:
x
∗
=
a
+
b
2
+
a
+
b
2
k
−
x
k
(2)
x^{*} =\frac{a+b}{2}+\frac{a+b}{2k}-\frac{x}{k} \tag2
x∗=2a+b+2ka+b−kx(2)
其中,
k
=
h
/
h
∗
k=h/h^{*}
k=h/h∗,
a
a
a和
b
b
b可以视为某维度的上下限。本文中的
k
k
k是一个与迭代次数相关的动态自适应值。
3. 部分代码展示
Fun_name='F1'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Coati (population members)
Max_iterations=500; % maximum number of iteration
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name); % Object function information
[Best_score_COA,Best_pos_COA,COA_curve]=COA(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness); % Calculating the solution of the given problem using COA
[Best_score_GWO,Best_pos_GWO,GWO_curve]=GWO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness); % 灰狼优化算法
[Best_score_WOA,Best_pos_WOA,WOA_curve]=WOA(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness); % 鲸鱼优化算法
[Best_score_SSA,Best_pos_SSA,SSA_curve]=SSA(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness); % 麻雀搜索算法
[Best_score_ICOA,Best_pos_ICOA,ICOA_curve]=ICOA(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
%%
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(Fun_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])
subplot(1,2,2);
% 灰狼优化算法
semilogy(GWO_curve,'Color','b','LineWidth',2)
hold on
% 鲸鱼优化算法
semilogy(WOA_curve,'Color','g','LineWidth',2)
hold on
% 麻雀搜索算法
semilogy(SSA_curve,'Color','m','LineWidth',2)
hold on
semilogy(COA_curve,'Color','k','LineWidth',2)
hold on
semilogy(ICOA_curve,'Color','r','LineWidth',2)
title(Fun_name)
xlabel('Iteration');
ylabel('Best fitness function');
axis tight
legend('GWO','WOA','SSA','COA','ICOA')
4. 仿真结果展示









5. 资源获取
可以获取完整代码资源。