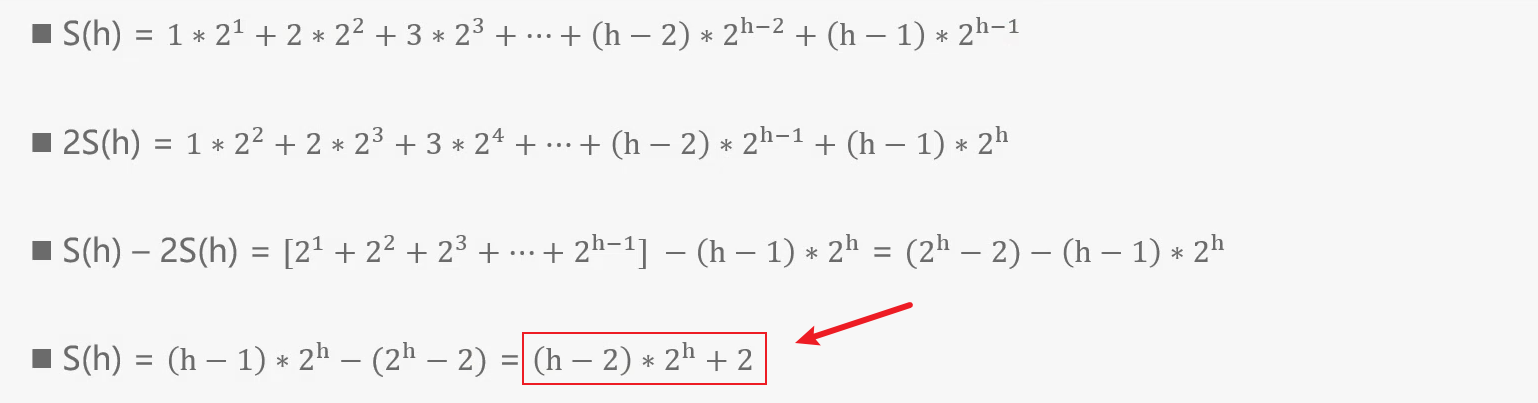二叉堆
我们现在有一个需求,用来存放整数,要求需要提供三个接口
- 添加元素
- 获取最大值
- 删除最大值
我们可以用我们熟悉的数据结构去解决这些问题
| 获取最大值 | 删除最大值 | 添加元素 | 描述 | |
|---|---|---|---|---|
| 动态数组/双向链表 | O(n) | O(n) | O(1) | O(n) 复杂度太高了 |
| (有序)动态数组/双向链表 | O(1) | O(1) | O(n) | 全排序有点浪费 |
| BBST | O(logn) | O(logn) | O(logn) | 杀鸡用了牛刀 |
| 堆 | O(1) | O(logn) | O(logn) | 最优 |

我们思考一下:
- 有序动态数组/双向链表:会全排序,我们其实更需要的是偏序
- BBST:每次二分,复杂度
O(logn),但是BBST太复杂了
那有没有更优的数据结构呢?当然有,那就是堆
1. Top K问题&二叉堆
1.1 Top K问题
我们将从海量数据中找出前K个数据的问题称之为Top K问题
例如从100w个整数中找出最大的100个整数。Top K问题的解法之一,就可以使用堆(heap)来解决
1.2 二叉堆
二叉堆的逻辑结构就是一棵
完全二叉树,所以也叫完全二叉堆
- 基于完全二叉树的特性,二叉堆的底层可以使用数组实现
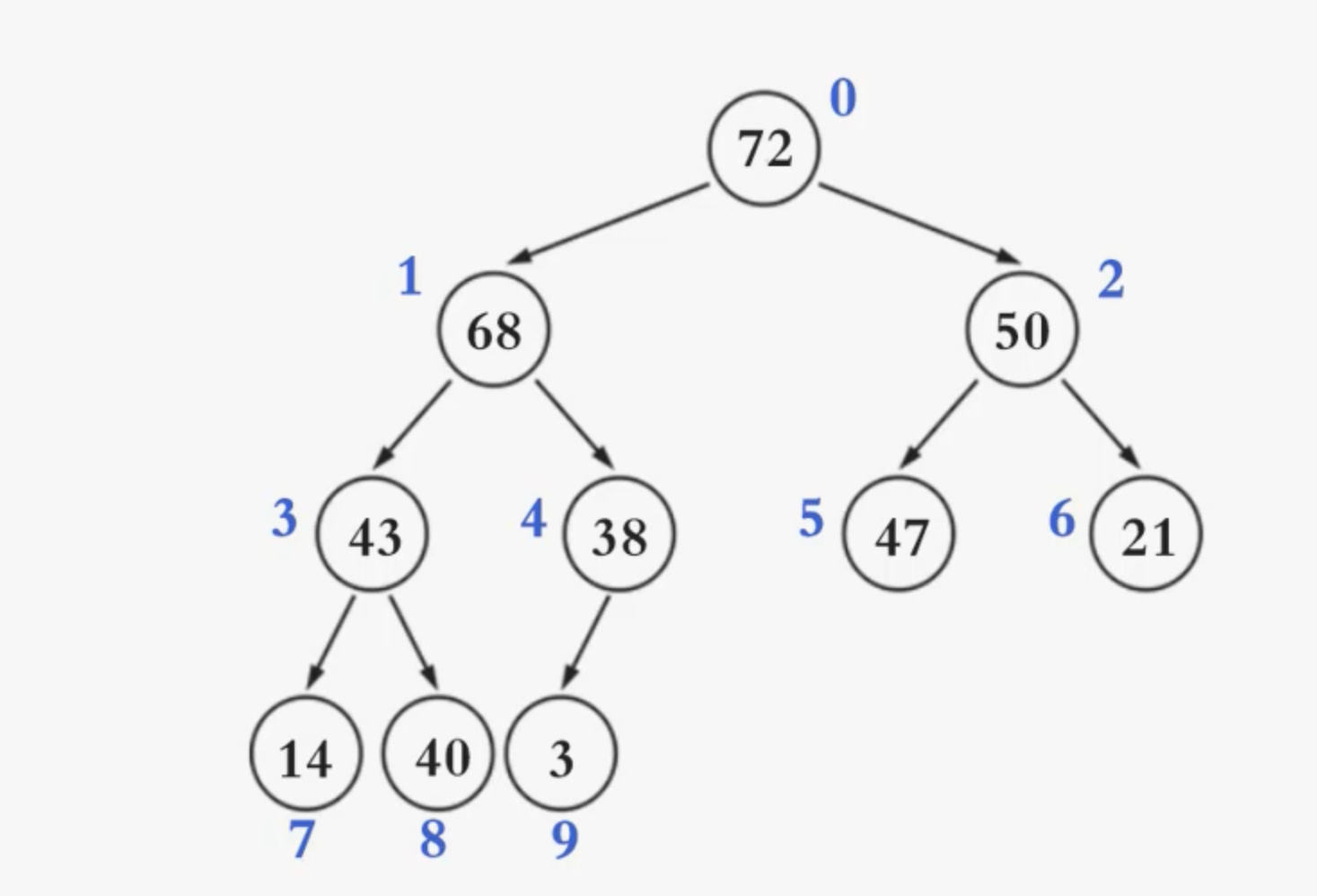
使用数组进行实现,相较于BBST来说较为简单,例如上面的堆我们用数组进行存储的实现为:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 72 | 68 | 50 | 43 | 38 | 47 | 21 | 14 | 40 | 3 |
观察索引i我们可以发现一些规律
- 如果
i = 0,它就是根结点 - 如果
i > 0,它的父结点编号为floor((i - 1) / 2) - 如果
2i + 1 <= n - 1,它的左子节点编号为2i + 1(n为堆元素的个数) - 如果
2i + 1 > n - 1,它无左子节点 - 如果
2i + 2 <= n - 1,它的右子节点编号为2i + 2 - 如果
2i + 2 > n - 1,它无右子节点
例如索引为5的结点的父结点的索引就是(5 - 1) / 2 = 2,值就是50;例如值为47的结点,序号为5,2 * 5 + 1 = 11 < 9,所以没有左子节点;例如值为38的结点,序号为4,2 * 4 + 1 = 9 <= 9,所以有左子节点,并且节点为2 * 4 + 1 = 9
1.3 堆(Heap)
堆(Heap)是一种树状的数据结构(不要跟内存模型中的
堆空间混淆),常见的堆有:
- 二叉堆(Binary Heap,完全二叉堆)
- 多叉堆(D-heap、D-ary Heap)
- 索引堆(Index Heap)
- 二项堆(Binomial Heap)
- 斐波拉契堆(Fibonacci Heap)
- 左倾堆(Leftist Heap,左式堆)
- 斜堆(Skew Heap)
堆最重要的性质是:任意结点的值总是大于或小于
子结点的值
- 如果任意结点的值总是
大于子结点,称为:最大堆、大根堆、大顶堆- 如果任意结点的值总是
小于子结点,称为:最小堆、小根堆、小顶堆
2. 实现
2.1 二叉堆基本接口
int size(); // 元素的数量
boolean isEmpty(); // 是否为空
void clear(); // 清空
void add(E element); // 添加元素
E get(); // 获得堆顶元素
E remove(); // 删除堆顶元素
E replace(E element); // 删除堆顶元素的同时插入一个新元素
2.2 二叉堆添加逻辑
假设我们现在有一棵二叉堆
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 72 | 68 | 50 | 43 | 38 | 47 | 21 | 14 | 40 | 3 |
现在需要添加一个元素80,如果按照数组进行实现,那么我们肯定首先是加上数组的最后面,即这样子:
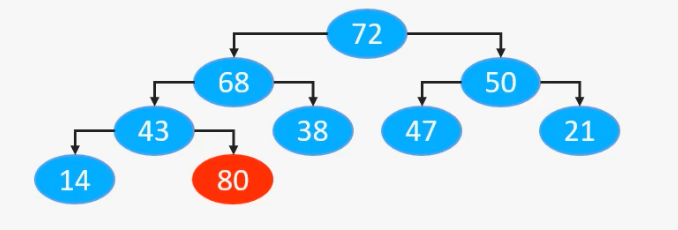
当然显然这样是不对的,不能满足二叉堆的性质,所以我们需要做的就是让添加的元素跟父结点进行比较,因为二叉堆性质就是父结点要比子结点大,即结点43要和14、80,进行比较,如果比子结点小,即交换位置
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 72 | 68 | 50 | 43 | 38 | 47 | 21 | 14 | 40 | 3 | 80 |
进行交换
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 72 | 68 | 50 | 80 | 38 | 47 | 21 | 14 | 40 | 3 | 43 |
然后发现还是比父结点大,则继续交换。知道比父结点小或者称为根结点为止
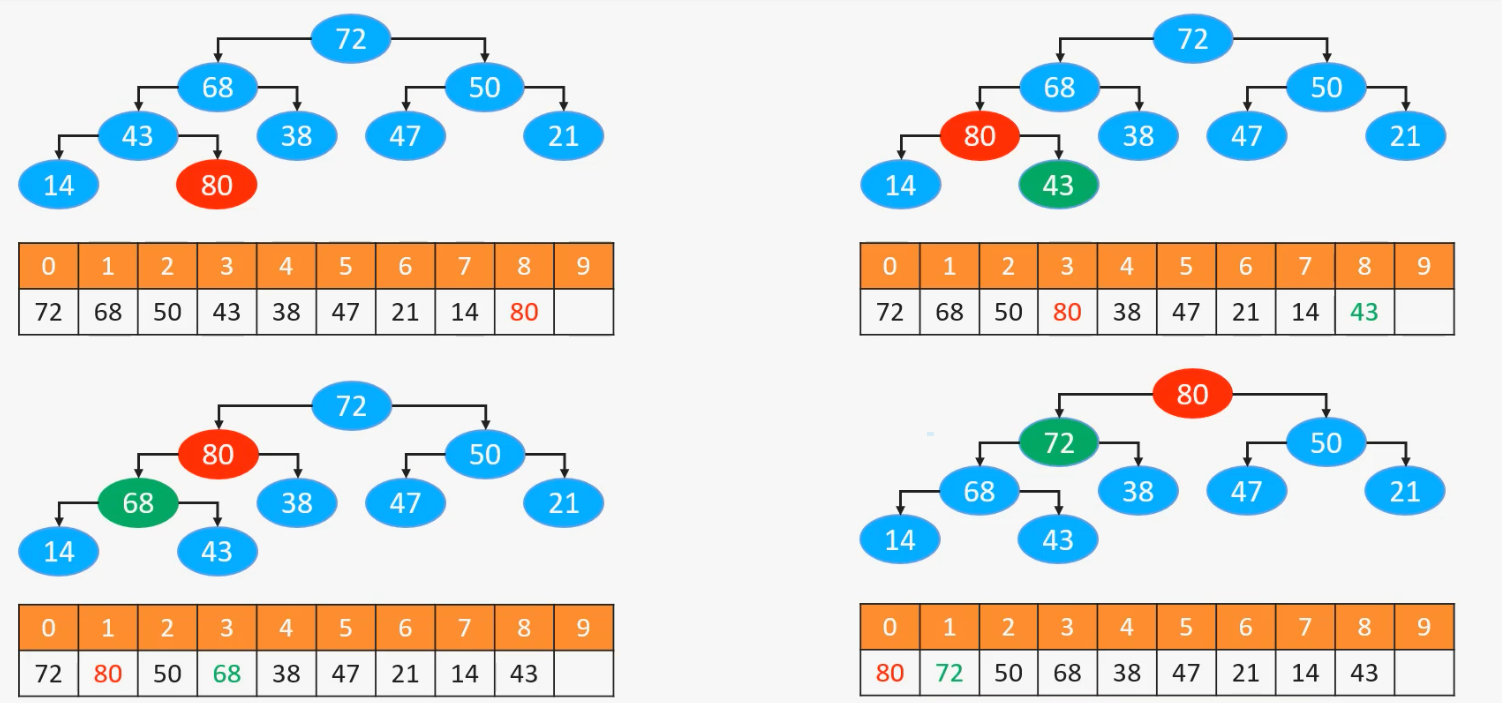
总结一下:
循环执行以下操作(图中的
80简称为 node)
- 如果node
>父结点,则与父结点交换位置- 如果node
<=父结点,或者node成为根结点,则退出循环我们将这个过程称为
上滤(Sift Up),时间复杂度为:O(logn)
写一下逻辑
/**
* 让index上的元素进行上滤
*
* @param index 元素在数组中的索引
*/
private void siftUp(int index) {
while (index > 0) {
// 检查父结点是否小于该元素
// 父结点编号为`floor(i - 1) / 2`
int parentIndex = (index - 1) >> 1;
if (compare(elements[index], elements[parentIndex]) <= 0) {
break;
}
// 交换元素
E tmp = elements[parentIndex];
elements[parentIndex] = elements[index];
elements[index] = tmp;
index = parentIndex;
}
}
@SuppressWarnings("unchecked")
private int compare(E e1, E e2) {
return comparator != null ? comparator.compare(e1, e2) : ((Comparable<E>) e1).compareTo(e2);
}
测试一下
@Test
public void TestSiftUp() {
BinaryHeap<Integer> heap = new BinaryHeap<>();
int[] arr = new int[]{68, 72, 43, 50, 38};
for (int i : arr) {
heap.add(i);
}
BinaryTrees.println(heap);
}
// 输出
┌─72─┐
│ │
┌─68─┐ 43
│ │
50 38
当然交换时候的代码还可以再优化一下
/**
* 让index上的元素进行上滤
*
* @param index 元素在数组中的索引
*/
private void siftUp(int index) {
E element = elements[index];
while (index > 0) {
int parentIndex = (index - 1) >> 1;
E parent = elements[parentIndex];
if (compare(element, parent) <= 0) break;
// 将父元素存储在index位置
elements[index] = parent;
// 重新赋值index
index = parentIndex;
}
elements[index] = element;
}
完整代码:
package com.fx.heap;
import com.fx.printer.BinaryTreeInfo;
import java.util.Arrays;
import java.util.Comparator;
/**
* <p>
* 默认为最大堆(大顶堆)
* </p>
*
* @author eureka
* @since 2023/5/18 21:42
*/
public class BinaryHeap<E> implements Heap<E>, BinaryTreeInfo {
private E[] elements;
private int size;
private Comparator<E> comparator;
private static final int DEFAULT_CAPACITY = 10;
@SuppressWarnings("unchecked")
public BinaryHeap(Comparator<E> comparator) {
this.comparator = comparator;
this.elements = (E[]) new Object[DEFAULT_CAPACITY];
}
@SuppressWarnings("unchecked")
public BinaryHeap() {
this.elements = (E[]) new Object[DEFAULT_CAPACITY];
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
Arrays.fill(elements, null);
return size == 0;
}
@Override
public void clear() {
size = 0;
}
@Override
public void add(E element) {
checkElementNotNull(element);
ensureCapacity(size + 1);
elements[size++] = element;
siftUp(size - 1);
}
@Override
public E get() {
checkEmpty();
return elements[0];
}
@Override
public E remove() {
return null;
}
@Override
public E replace(E element) {
return null;
}
/**
* 让index上的元素进行上滤
*
* @param index 元素在数组中的索引
*/
private void siftUp(int index) {
E element = elements[index];
while (index > 0) {
int parentIndex = (index - 1) >> 1;
E parent = elements[parentIndex];
if (compare(element, parent) <= 0) break;
// 将父元素存储在index位置
elements[index] = parent;
// 重新赋值index
index = parentIndex;
}
elements[index] = element;
}
@SuppressWarnings("unchecked")
private int compare(E e1, E e2) {
return comparator != null ? comparator.compare(e1, e2) : ((Comparable<E>) e1).compareTo(e2);
}
private void checkEmpty() {
if (size == 0) {
throw new IndexOutOfBoundsException("heap is empty");
}
}
private void checkElementNotNull(E element) {
if (element == null) {
throw new IllegalArgumentException("there element not null");
}
}
/**
* 保证集合容量足够
*/
private void ensureCapacity(int capacity) {
int oldCapacity = elements.length;
if (capacity < oldCapacity) return;
// 扩容1.5倍
int newCapacity = oldCapacity + (oldCapacity >> 1);
elements = Arrays.copyOf(elements, newCapacity);
}
@Override
public Object root() {
return 0;
}
@Override
public Object left(Object node) {
Integer index = (Integer) node;
int leftIndex = (index << 1) + 1;
return leftIndex >= size ? null : leftIndex;
}
@Override
public Object right(Object node) {
Integer index = (Integer) node;
int rightIndex = (index << 1) + 2;
return rightIndex >= size ? null : rightIndex;
}
@Override
public Object string(Object node) {
return elements[(Integer) node];
}
}
2.3 删除逻辑
我们发现我们的删除接口是这样的:
E remove(); // 删除堆顶元素
我们发现删除时我们并没有传入索引,因为我们只需要删除最大的元素即可。如果我们按照数组的删除逻辑,那就是直接将index为0的元素删除,然后其他元素往前移动,这样当然是没有什么问题的,但是这样的时间复杂度就是O(n)级别了,不满足我们log(n)的要求
那么如果我们将index为0的元素和最后面的元素交换,然后删除最后一个元素的话,这样可以吗?
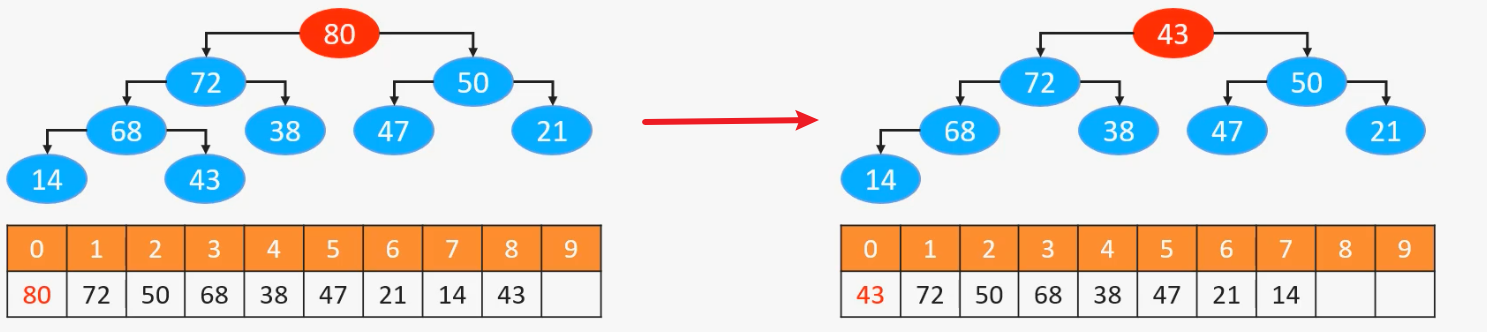
我们会发现我们这样做的话,43会变成根结点,但是不满足堆的性质了
这时候我们需要将根结点和最大的子结点进行交换,知道交换不了为止,也就是下面的过程
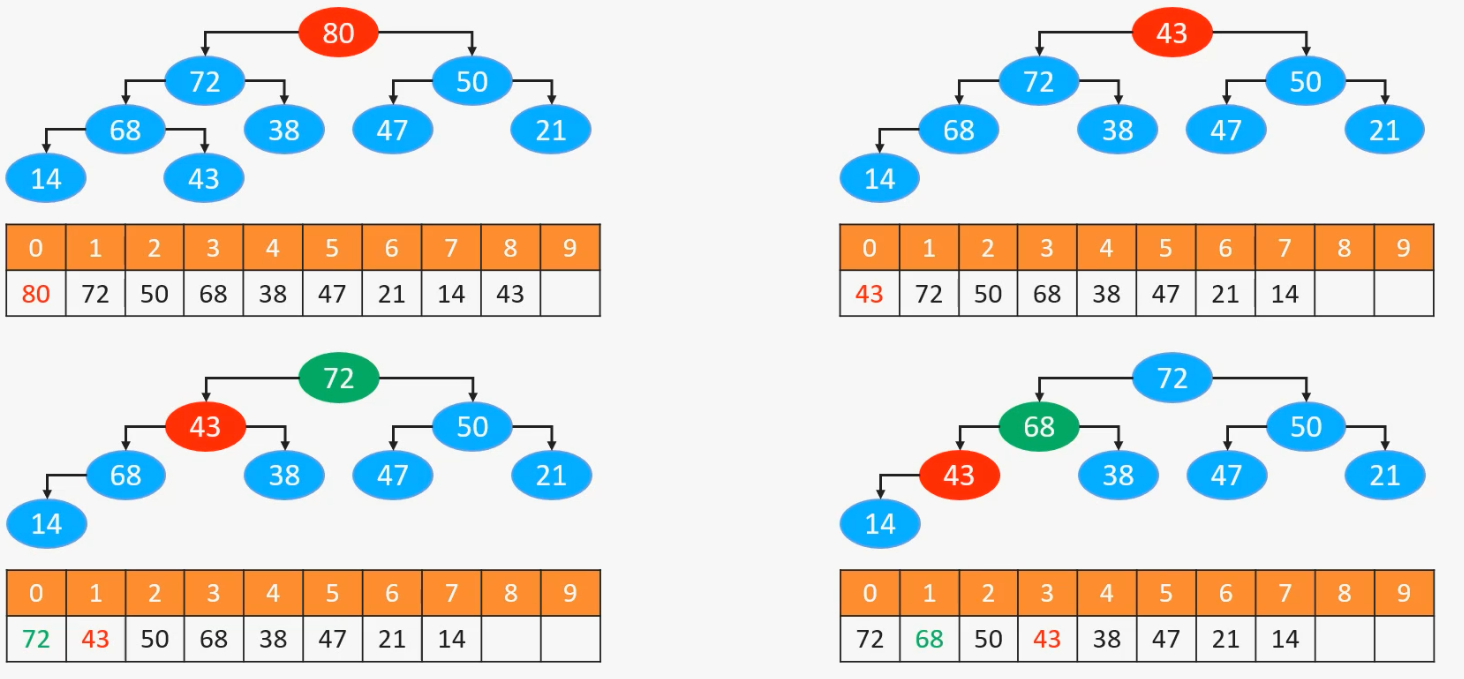
当交换完成之后,堆的性质将得到维护,我们总结一下过程:
- 用最后一个结点覆盖根结点
- 删除最后一个结点
- 循环以下的步骤(图中的
43简称为node)
我们将这个过程称之为下滤(Sift Down),时间复杂度log(n)
在下滤的过程中,我们需要注意要下滤的结点必须要有子结点,即不能是叶子结点,根据完全二叉树的性质:
-
如果当前结点为叶子结点,那么后面的结点也都是叶子节点
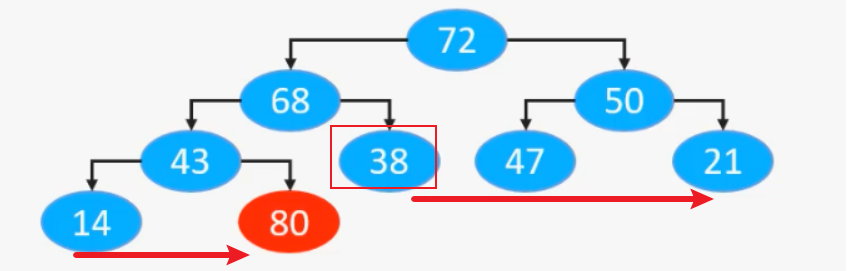
-
第一个叶子结点的索引等于非叶子结点的数量
-
非叶子结点的数量等于
floor(n / 2)
我们来写一下代码:
@Override
public E remove() {
checkEmpty();
// 用最后一个结点覆盖根结点
E root = elements[0];
// size也要减一
elements[0] = elements[size - 1];
elements[size - 1] = null;
size--;
// 进行下滤
siftDown(0);
return null;
}
/**
* 下滤
*
* @param index 结点的索引
*/
private void siftDown(int index) {
// 不能是叶子结点(必须要有子结点)
int half = size >> 1;
E element = elements[index];
while (index < half) {
// index 的节点有两种情况
// 1. 只有左子节点 2. 同时有左右子节点
// 默认跟左子节点进行比较
int childIndex = (index << 1) + 1;
E childElement = elements[childIndex];
// 右子节点
int rightIndex = childIndex + 1;
// 选出左右子节点中最大的
if (rightIndex < size && compare(elements[rightIndex], elements[childIndex]) > 0) {
childIndex = rightIndex;
childElement = elements[rightIndex];
}
if (compare(element, childElement) >= 0) {
break;
}
// 将子结点存放到index位置
elements[index] = childElement;
index = childIndex;
}
elements[index] = element;
}
测试
@Test
public void TestSiftUp() {
BinaryHeap<Integer> heap = new BinaryHeap<>();
int[] arr = new int[]{68, 72, 43, 50, 38, 30, 12, 15, 78};
for (int i : arr) {
heap.add(i);
}
BinaryTrees.println(heap);
System.out.printf("删除结点%s后\n", heap.remove());
BinaryTrees.println(heap);
}
// 输出
┌───78──┐
│ │
┌─72─┐ ┌─43─┐
│ │ │ │
┌─68─┐ 38 30 12
│ │
15 50
删除结点78后
┌───72──┐
│ │
┌─68─┐ ┌─43─┐
│ │ │ │
┌─50 38 30 12
│
15
2.4 replace逻辑
replace逻辑是先删除堆顶元素,然后再将要替换的元素放入堆中(相当于将堆顶元素替换,然后下滤)
我们可以先调用remove()方法,再调用add()方法,但是这样时间复杂度有两个log(n),所以我们可以这样写:
public E replace(E element) {
checkElementNotNull(element);
E root = null;
if (size == 0) {
elements[0] = element;
size++;
} else {
root = elements[0];
elements[0] = element;
siftDown(0);
}
return root;
}
2.5 Heapify批量建堆
什么是
Heapify批量建堆呢?我们将无序的数组快速转换为堆的过程称之为
Heapify(批量建堆)
我们第一时间想到的肯定是直接调用add方法,比如这样:
@Test
public void TestHeapify() {
BinaryHeap<Integer> heap = new BinaryHeap<>();
int[] arr = new int[]{75, 57, 65, 13, 34, 79, 9, 23, 31, 27, 7, 3, 37, 90, 48, 95, 11, 32, 41};
for (int i : arr) {
heap.add(i);
}
BinaryTrees.println(heap);
}
// 打印
┌───────95──────┐
│ │
┌────90────┐ ┌──79──┐
│ │ │ │
┌───57──┐ ┌─34─┐ ┌─65─┐ ┌─75─┐
│ │ │ │ │ │ │ │
┌─31─┐ ┌─41─┐ 27 7 3 37 9 48
│ │ │ │
13 11 23 32
这样当然可以,其实也就相当于自上而下的上滤,对于批量建堆,我们一般有两种办法:
- 自上而下的上滤
- 自下而上的下滤
2.5.1 自上而下的上滤
自上而下的上滤很简单,只需要从第二个元素开始每个元素都进行上滤操作(第一个元素不需要)
整个过程是这样的
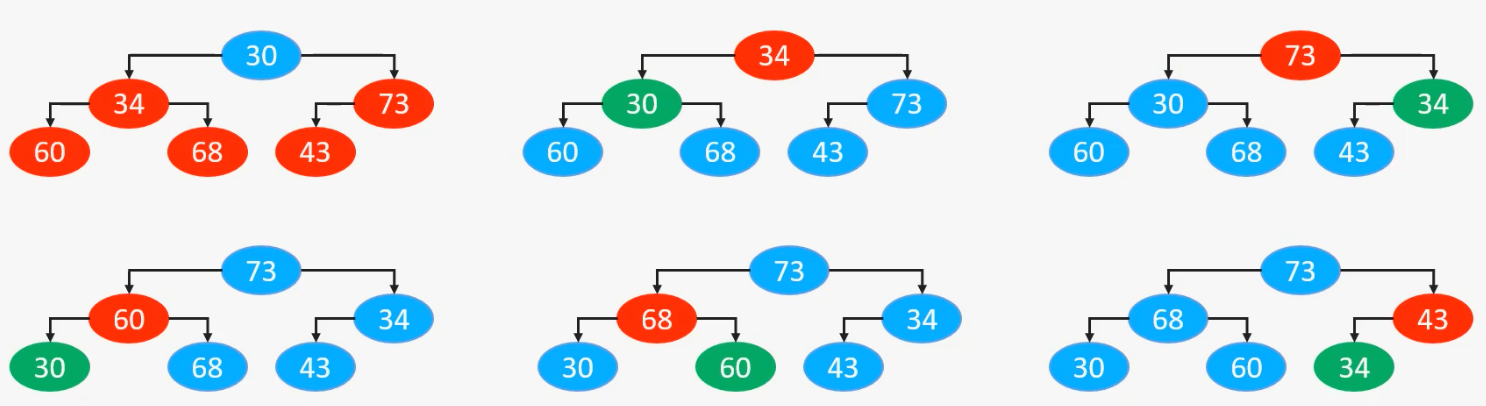
伪代码如下:
// 注意这里i是从1开始的哦
for(int i = 1; i < size; i++) {
siftUp(i);
}
2.5.2 自下而上的下滤
自下而上的下滤的过程也比较简单,从最后一个元素开始下滤,但是这里需要注意的是,叶子结点是不需要下滤的,因为不能往下了已经,所以关键代码是:
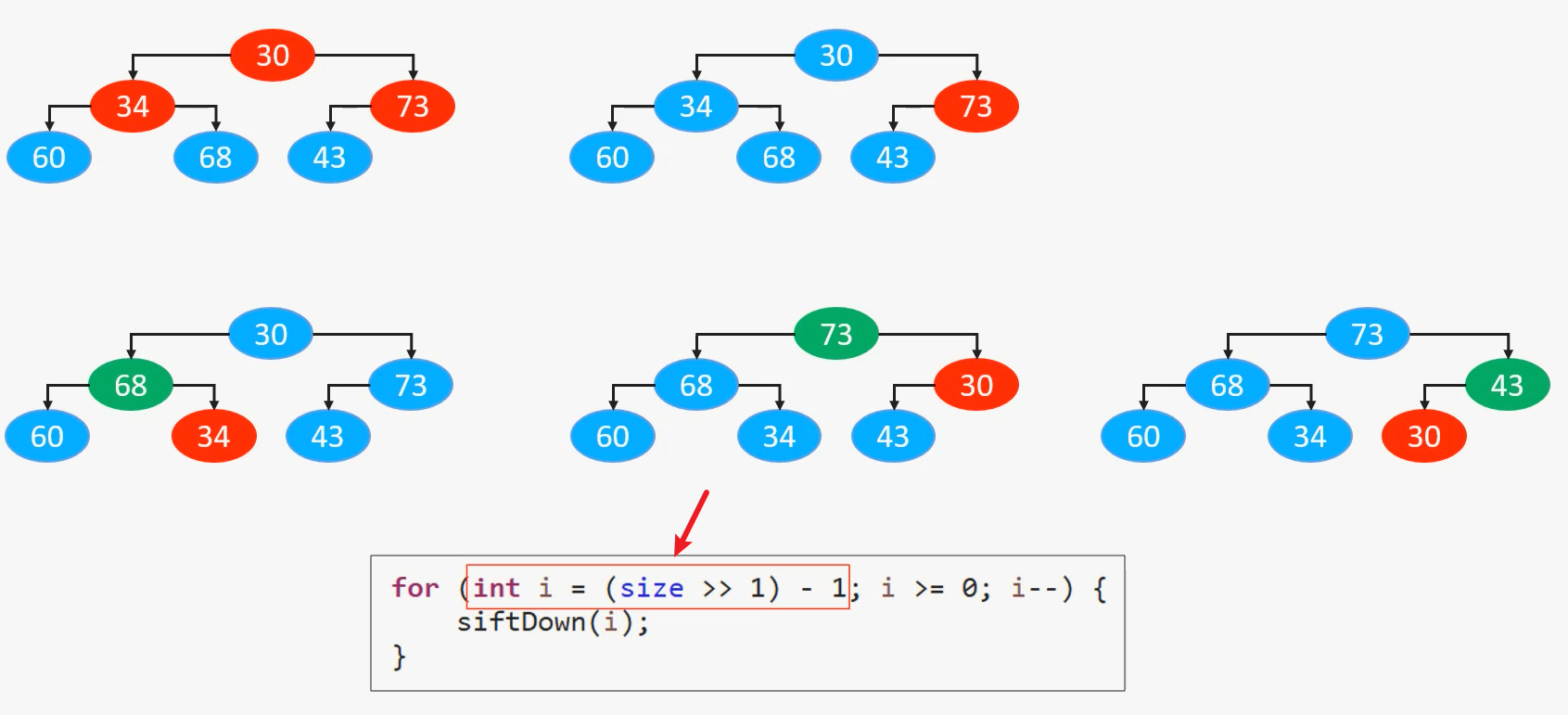
关键代码如下:
private void heapify() {
// 自下而上的下滤
for (int i = (size >> 1) - 1; i >= 0; i--) {
siftDown(i);
}
}
2.5.3 两种方式对比
两种方式进行批量建堆的时间复杂度如下,可以看出由于在自下而上的下滤中,叶子结点是不需要进行下滤操作的,并且只有尽可能少的结点需要完成尽可能复杂的下滤操作,所以时间复杂度较优
为什么自上而下的上滤复杂度比较高呢?这是因为相当于做了全排序,但是二叉堆其实是偏序的
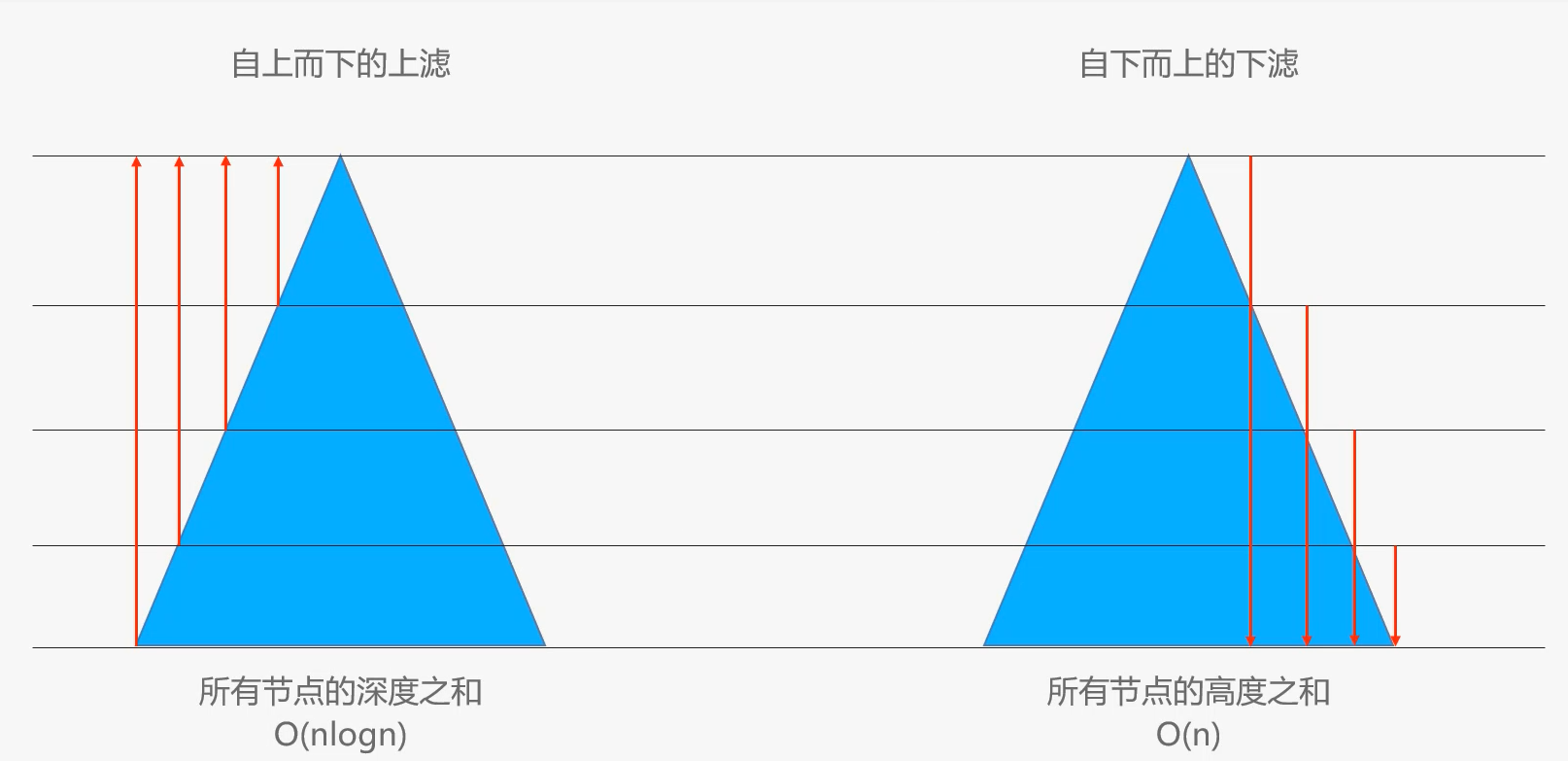
自上而下的上滤相当于所有结点的深度之和
- 仅仅是叶子节点,就有近 n/2 个,而且每一个叶子节点的深度都是 O(logn) 级别的
- 因此,在叶子节点这一块,就达到了 O(nlogn) 级别
- O(nlogn) 的时间复杂度足以利用排序算法对所有节点进行全排序
自下而上的下滤相当于所有结点的高度之和,时间复杂度推导过程如下
其中第三步,中括号里面的其实就是一个等差数列和一个等比数列的乘积求通项公式的问题,可以使用
错位相减法
2.6 最小堆
我们只需要改变我们的比较逻辑,即可变为最小堆
@Test
public void Test() {
Integer[] arr = new Integer[]{75, 57, 65, 13, 34, 79, 9, 23, 31, 27, 7, 3, 37, 90, 48, 95, 11, 32, 41};
BinaryHeap<Integer> heap = new BinaryHeap<>(arr, (o1, o2) -> o2 - o1);
BinaryTrees.println(heap);
}
// 输出
┌─────────3────────┐
│ │
┌─────7────┐ ┌───9───┐
│ │ │ │
┌───11──┐ ┌─27─┐ ┌─37─┐ ┌─48─┐
│ │ │ │ │ │ │ │
┌─13─┐ ┌─31─┐ 57 34 79 65 90 75
│ │ │ │
95 23 32 41
3. TopK问题
TopK问题指的是:从n个整数中,找到最大的前k个数(k远远小于n)的问题
- 使用排序算法(例如快排),最优需要
O(nlogn)的时间复杂度- 使用二叉堆,时间复杂度为
O(nlogk)这里因为k远远小于n,所以二叉堆更优
如果我们从海量数据里找最大的数,其实我们使用的是小顶堆来实现,步骤如下:
- 新建一个小顶堆
- 扫描n个整数
- 先将遍历到的前k个数放入堆中
- 从第
k+1个数开始,如果大于堆顶元素,就使用replace操作(删除堆顶元素,将第k+1个数添加到堆中)
- 扫描完毕后,堆中剩下的就是最大的前k个数了
同理,如果我们需要找到最小的前k个数,就使用大顶堆,如果小于堆顶元素,则使用replace操作
@Test
public void TestTopK() {
Integer[] arr = new Integer[]{75, 57, 65, 13, 34, 79, 9, 23, 31, 27, 7, 3, 37, 90, 48, 95, 11, 32, 41};
BinaryHeap<Integer> heap = new BinaryHeap<>((o1, o2) -> o2 - o1);
int k = 5;
for (int i = 0; i < arr.length; i++) {
if (heap.size() < k) { // 前k个数添加到小顶堆
heap.add(arr[i]);
} else if (arr[i] > heap.get()) { // 如果是第k+1个数
heap.replace(arr[i]);
}
}
BinaryTrees.println(heap);
// 输出最大的前五个
Arrays.stream(arr)
.sorted((o1, o2) -> o2 - o1)
.limit(k)
.forEach(e -> System.out.print("\t" + e));
}
// 输出
┌─65─┐
│ │
┌─75─┐ 95
│ │
90 79
95 90 79 75 65
4. 堆排序
public class HeapSort {
public static void sort(int[] arr) {
int n = arr.length;
// 建立最大堆
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 一个个从堆顶取出元素,并放到数组末尾
for (int i = n - 1; i > 0; i--) {
// 把堆顶和当前未排定区域的最后一个元素交换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 对剩下的元素重新建立最大堆
heapify(arr, i, 0);
}
}
private static void heapify(int[] arr, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// 如果左子节点比根节点大,则将左子节点设为最大值
if (left < n && arr[left] > arr[largest])
largest = left;
// 如果右子节点比根节点大,则将右子节点设为最大值
if (right < n && arr[right] > arr[largest])
largest = right;
// 如果最大值不是根节点,则交换它们的位置
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// 递归调用,保证交换后的子树仍满足最大堆性质
heapify(arr, n, largest);
}
}
}
测试
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
HeapSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
// 输出
11, 12, 22, 25, 34, 64, 90
附录:源码地址
- 堆