文章目录
- 1. 图像超分辨率(Super Resolution)
- 1.1 概念
- 1.2 目标
- 1.3 应用
- 1.4 分类
- 1.4-2 单图超分的解决思路
- 1.5 ill-posed problem和算子
- 2. 经典超分辨率算法(稀疏编码Sparse Coding)
- 2.1 基本概念
- 2.2 基本流程
- 2.3 缺点
- 3. 深度学习时代的超分辨率算法
- 3.1 SRCNN
- 3.1.1 基本网络模型
- 3.1.2 三个卷积层的作用
- 3.1.3 训练和评价
- 3.1.4 效果展示
- 3.1.5 缺点
- 3.2 FSRCNN(Fast SRCNN2016)
- 3.2.1 转置卷积
- 3.2.2 模型
- 3.2.3 FSRCNN的优势
- 3.2.4 转置卷积的缺陷(FSRCNN的缺陷)
- 3.2.5 SRResNet2016(使用resnet和次像素卷积)
- 3.3 损失函数
- 3.3.1 均方误差
- 3.3.2 感知损失
- 3.4 对抗生成网络GAN简介
- 3.4.1 概念
- 3.4.2 应用
- 3.4.3 用神经网络表示和学习数据分布(GAN)
- 3.5 基于GAN的模型SRGAN
- 3.6 基于GAN的模型ESRGAN
- 3.5 视频超分辨率介绍
- 4. 实践MMEditing 1
视频链接:底层视觉与MMEditing
主讲:吕健勤 南洋理工大学副教授
1. 图像超分辨率(Super Resolution)
1.1 概念

- 图像超分辨率技术:把图像从低分辨率重构成高分辨率图像,有难度;
- 上面左图存在大量低频信息,但是高频信息非常少,在没有任何背景/先验知识的情况下,其实很难恢复到右边的样子(这其实就是下面单图超分不适定问题的解决思路,利用先验知识)
1.2 目标

最简单的提高图像分辨率的方法就是插值,
- 常见的就是双线性或者双立方插值
- 但是这种传统的插值方法并不能恢复图像的高频细节,只是对低分辨率的图做了比较好的等比例放大,低分辨率图不包含的高频细节,插值后的结果也不会凭空产生
1.3 应用

经典游戏高清重制

动画高清重制

照片修复

节省传输带宽(视频、图像等,改善用户体验,加载问题)
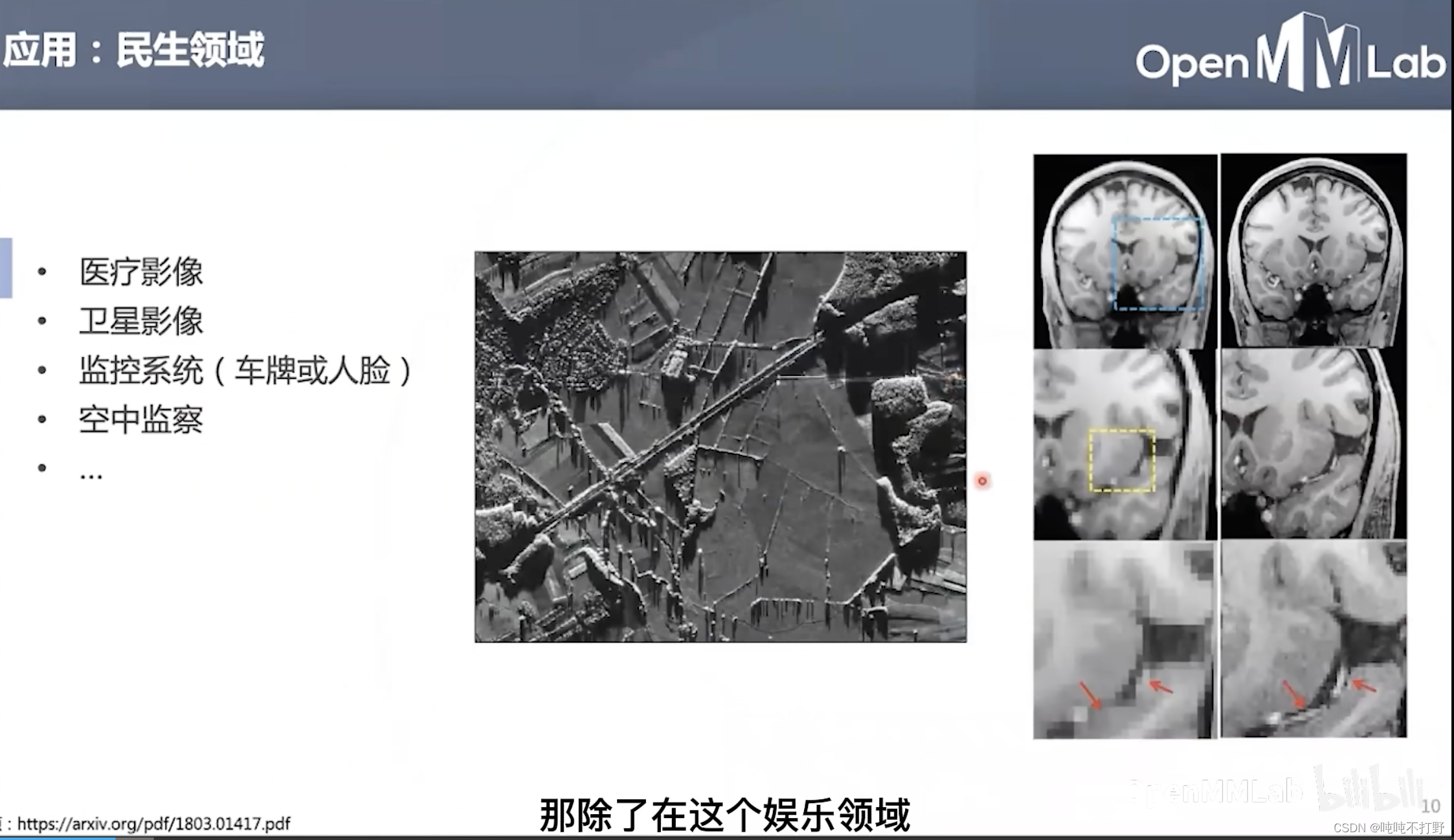
民生领域:
- 医疗影像和卫星影像
- 监控(车牌/人脸)
- 空中侦查
1.4 分类
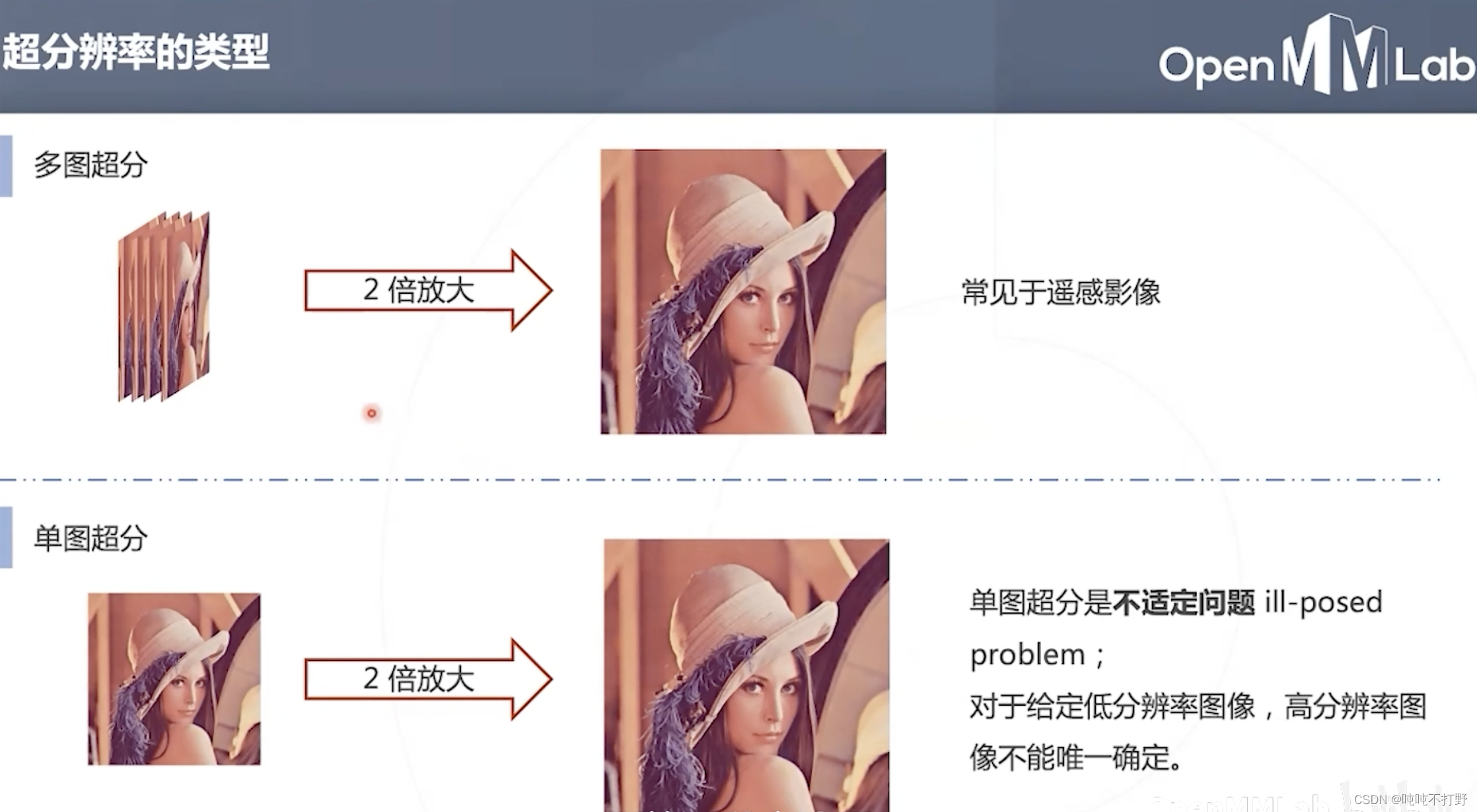
第一种:利用多张图(多帧)进行分辨率放大
- 利用多帧低清晰度的图像,通过一定的重建算法,得到高清晰度的图像
- 有点像之前3D姿态估计,利用多张图去进行估计,还是利用多帧比单帧会有更多信息的优势
- 常见于遥感影像或者视频超分
第二种:单图超分
- 单图超分是一个不适定问题(ill-posed problem,名词解释详见1.5 ill-posed problem)
- 即:对于一个给定的低分辨率图像,其重建后的高分辨率图像并不唯一(相当于一个函数,输入同一个x,得到了不同的y,这就不是函数)
1.4-2 单图超分的解决思路
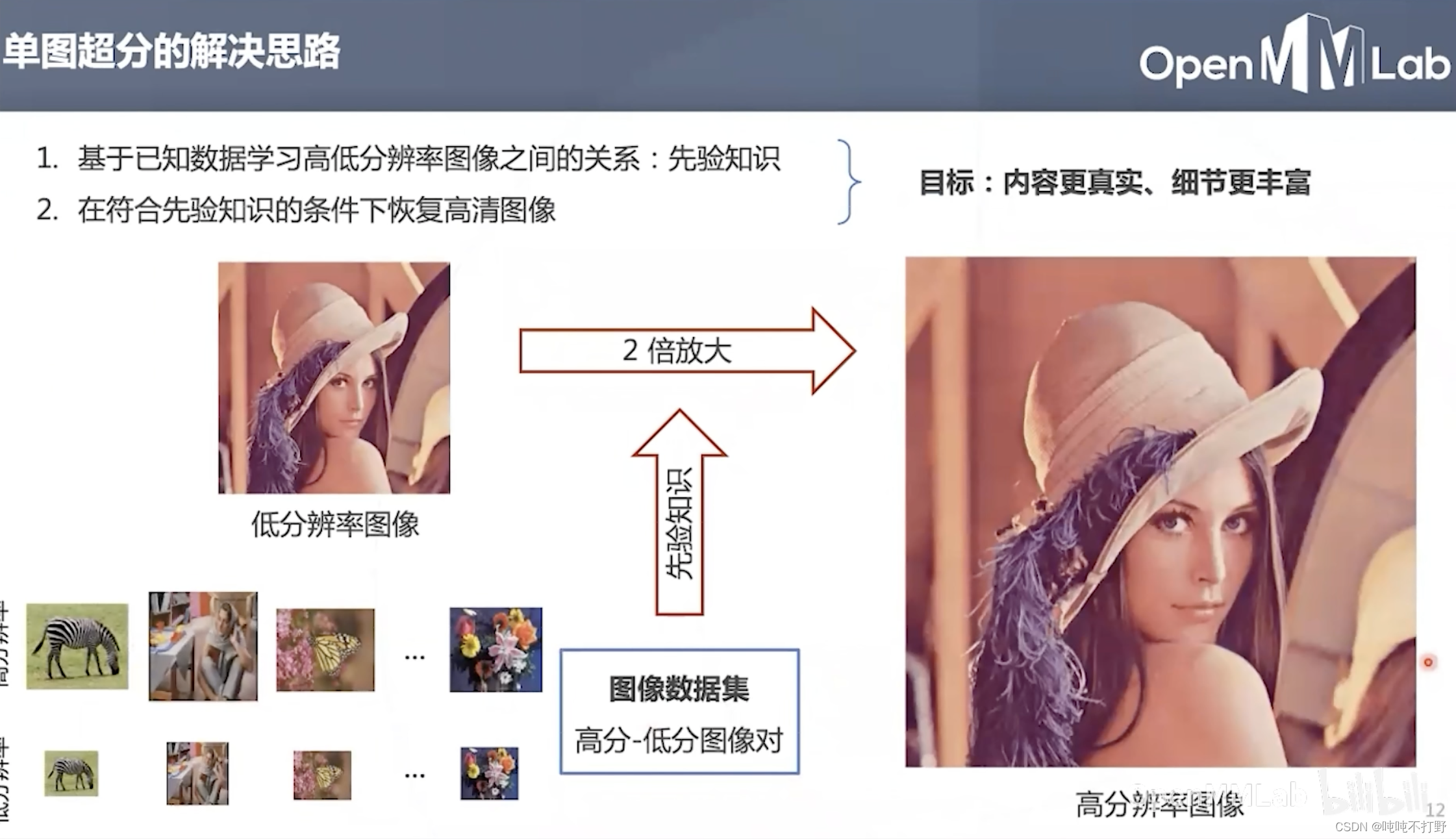
虽然单图超分是个不适定问题/病态问题,但是也有一定的方法可以解决,比如:利用先验知识
- 高分辨率和低分辨率图像对之间存在一些内部规律,学习这些规律作为先验知识
- 在符合先验知识的条件下恢复高清图像
即:单图超分是个病态问题,输入同一个低分辨率图像,可能会输出多种高分辨率图像
- 如何从多个输出中选出最合适的那一个,就是要解决的问题
- 这里的解决方案是:如果恢复出的图像符合先验知识,那么它就是最合适的那个
- 符合先验知识,则重建出的高分辨率图像的内容就会更真实,细节也会更丰富
- 所以需要保证先验知识是朝着这内容真实、细节丰富着两个目标去的
1.5 ill-posed problem和算子

在mmpose视频中,那个老师说 从2D图像得到3D姿态估计就是个病态问题,这里的病态指的就是解不唯一
可以想一下高数里函数的概念:

输入一个2d图像,经过模型,得到的3D姿态估计结果不唯一,所以不符合函数/映射的定义,是个病态问题

映射也称为算子,所以之前那些什么canny边缘算子,sober算子就是种映射,同时由于全是实数域,所以就是个函数
以下内容转自:计算机视觉中的不适定问题(ill-posed problem)
- 适定问题(well-posed problem)和不适定问题(ill-posed problem)都是数学领域的术语。
- 前者需满足三个条件,若有一个不满足则称为"ill-posed problem":
- a solution exists
解必须存在 - the solution is unique
解必须唯一 - the solution’s behavior changes continuously with the initial conditions.
解能根据初始条件连续变化,不会发生跳变,即解必须稳定
- a solution exists
- 在计算机视觉中,有很多任务不满足“适定”条件,通常不满足第二条和第三条。
- 比如用GAN“伪造”图像的时候,这个任务就不满足“解的唯一性”。
- 做图像超分辨率,或者对图像去雨去雾去模糊等等任务时,这些都没有一个标准答案,解有无数种。更重要的是,这些解都是不稳定的。
- 不适定问题就是:一个输入图像会对应多个合理输出图像,而这个问题可以看作是从多个输出中选出最合适的那一个。
2. 经典超分辨率算法(稀疏编码Sparse Coding)
2.1 基本概念
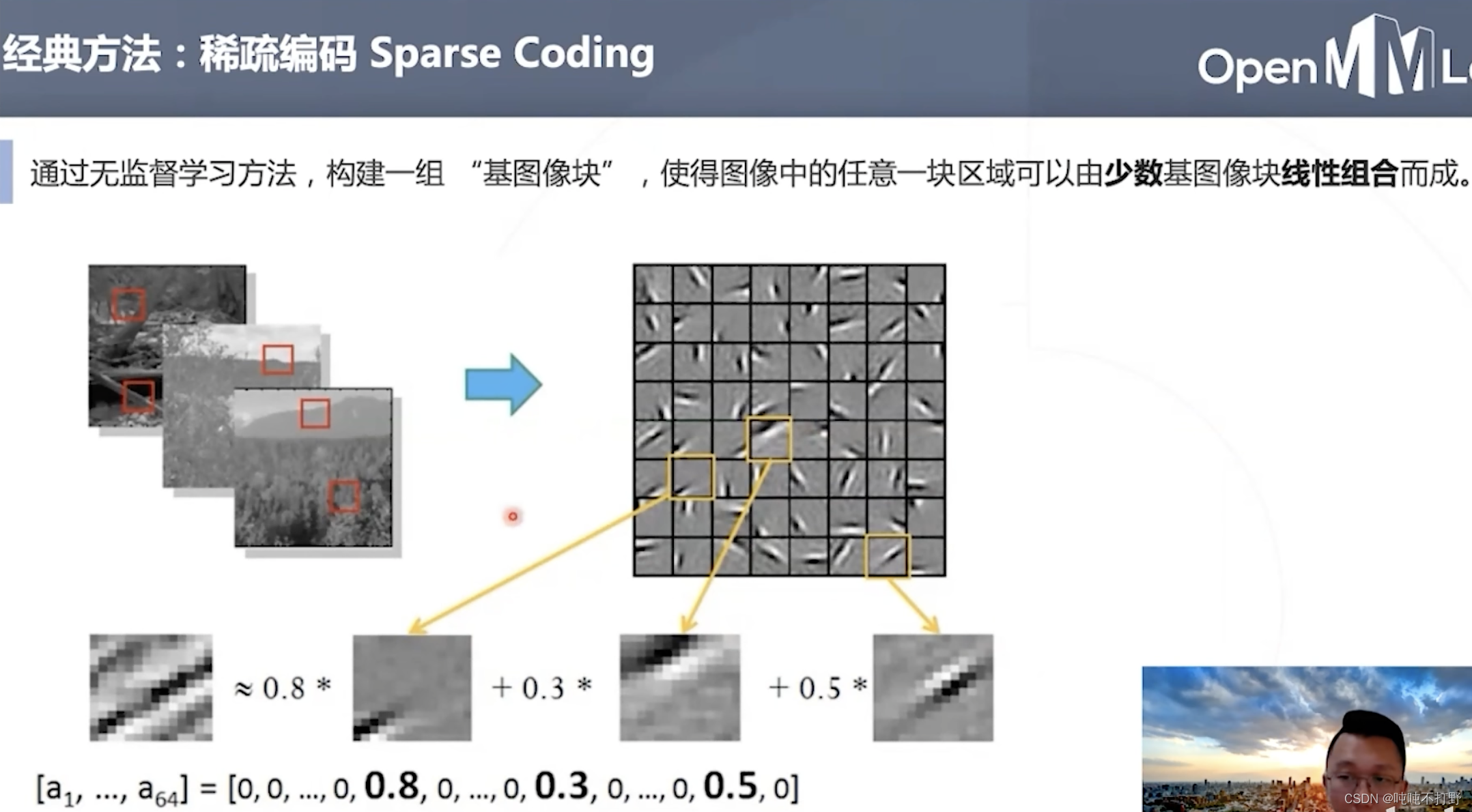
传统的超分算法主要是基于稀疏编码,关于稀疏编码:
- 是一种无监督方法,
- 针对图像,构建一组字典,使得图像中任意一块区域可以由字典中少量的基图像块线性组合而成。
- 相当于一个向量可以由一个坐标系里的基向量构成(坐标系里任意一个向量=基向量的线性组合)
- 这里就是图像中任意一个区域,由字典里的基图像构成(图像中任意一个区域=基图像的线性组合)
- 上图右边就是构建的基图像字典,左边就是原图,下面的公式就表示左图中的一个区域用基图像的线性组合表示
- 傅里叶变换好像也是把一个波分解成多个基础波,挺像的其实
2.2 基本流程
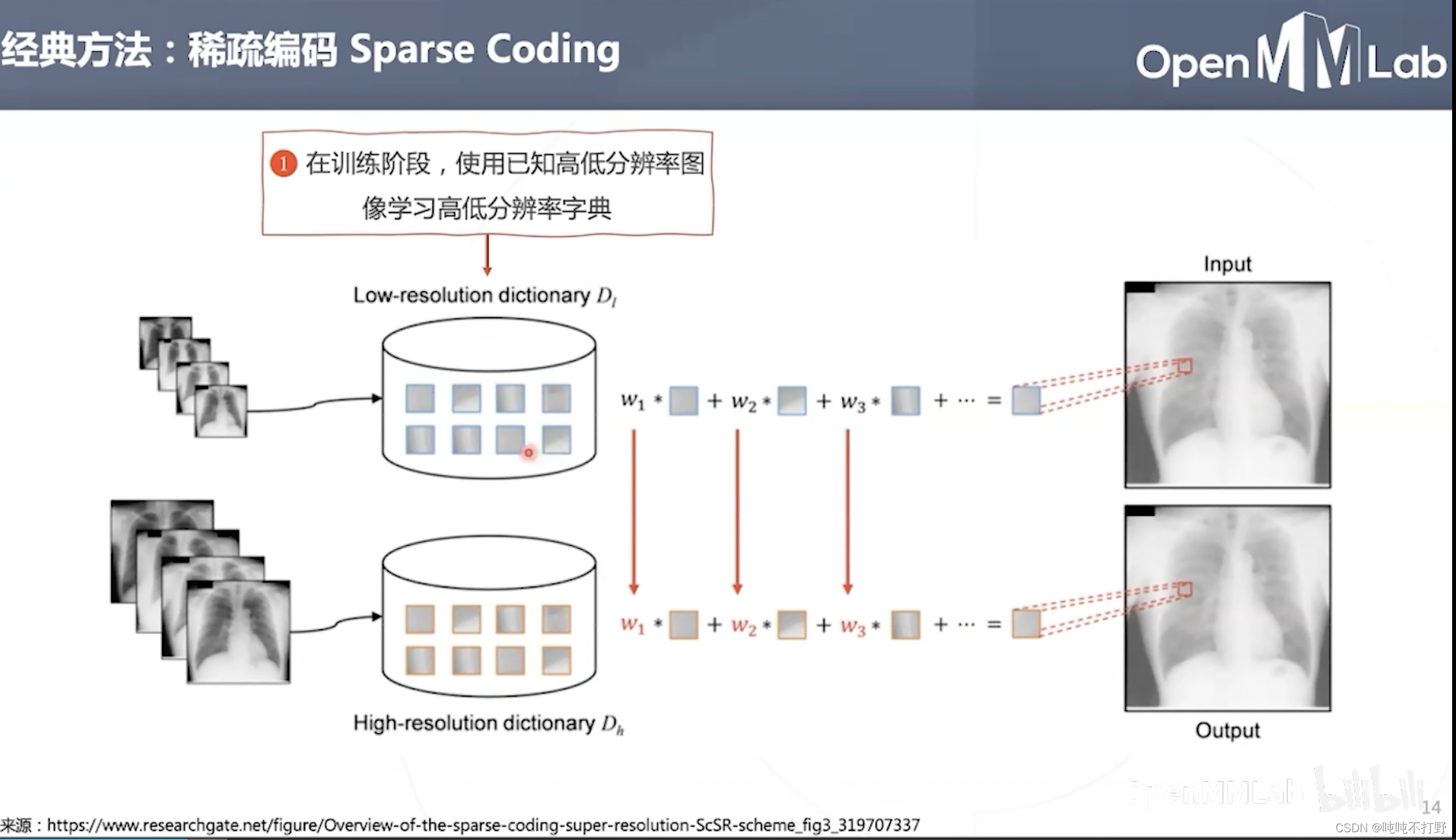
完整步骤:
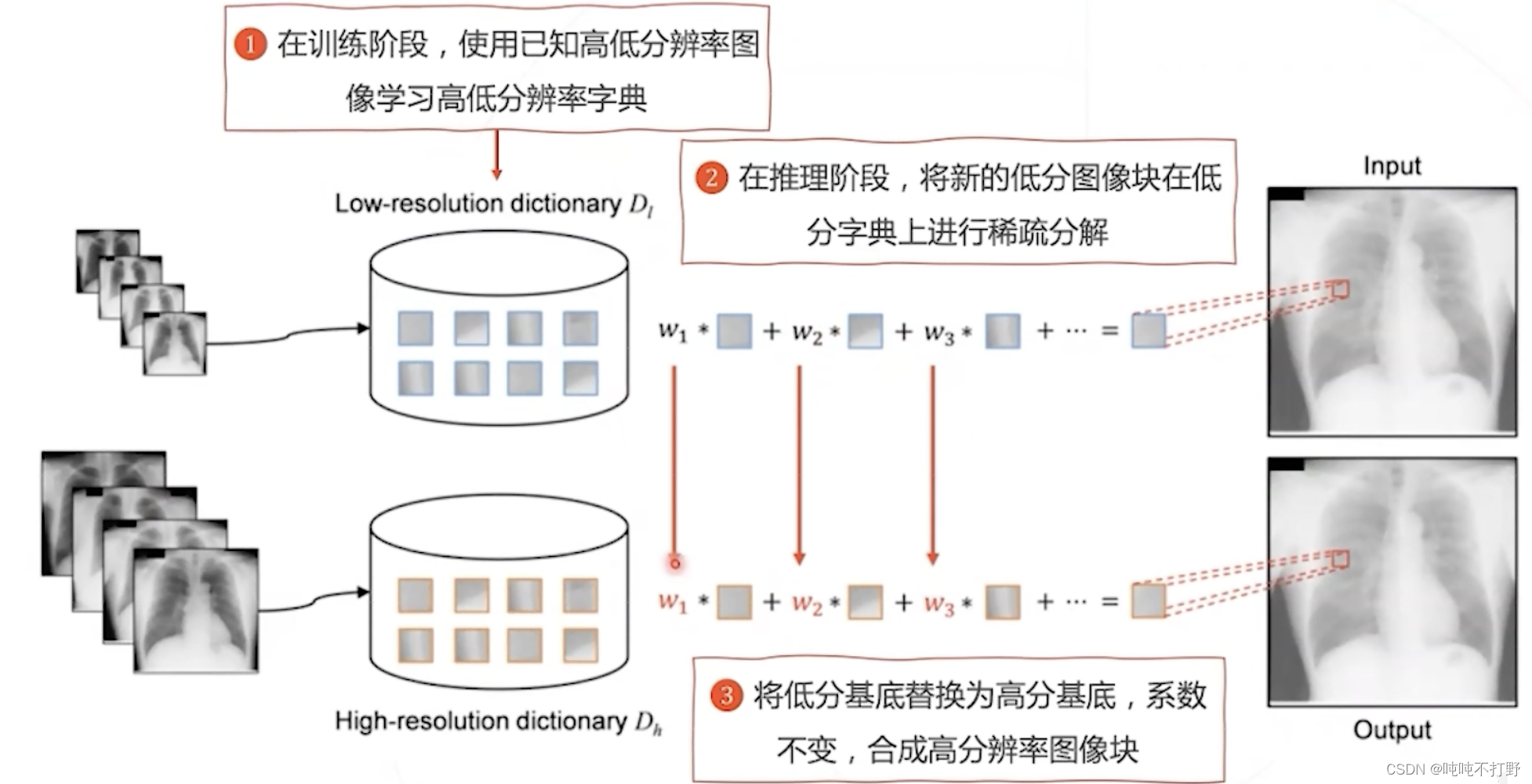
上面说到超分是个不适定问题,需要用强先验来约束这个解。可以回想一下 拉格朗日约束求极值,详见:动手学深度学习V2.0(Pytorch)——12. 权重衰退中3 拉格朗日约束求极值 扩展
- 在训练阶段:为了得到先验,需要我们有高低分辨率配对的图像(输入),使用已知的高低分辨率图像分别训练高低分辨率字典(用高分辨率图像学习高分辨率字典,低分辨率同理)
- 在推理阶段:
- 将新的低分辨率图像(待推理图像),在低分字典上进行稀疏分解,相当于得到低分辨率图像基图像的线性表示。
- 将低分基底替换成高分基底,系数不变,得到高分辨率图像块。
- 有点像坐标系变换的感觉,比如,有个向量在A坐标系下坐标是(1,3,8),将其进行旋转,只需要修改坐标系,就可以继续保持其坐标是(1,3,8)。表示/描述方法变了,但是本质特征没变。有个研究方向就是表示学习,比如NLP的词袋模型、word2vec都属于表示方法

- 这里低分辨率是原始的表示,高分辨率是我们希望得到的更好的表示
2.3 缺点

- 对低分辨率图像块进行系数分解,得到系数仍然是一个相对复杂的优化问题。(有一丢丢矩阵分解的感觉,哈哈哈,推荐系统里,不过还不太一样)
- 训练和推理阶段都很耗时
3. 深度学习时代的超分辨率算法

一般有两个方向:
- 使用卷积神经网络和普通损失函数,端到端从低分辨率图像恢复高分辨率图像,例如:SRCNN和FSRCNN
- 使用生成对抗网络
3.1 SRCNN
3.1.1 基本网络模型
arxiv论文:Image Super-Resolution Using Deep Convolutional Networks
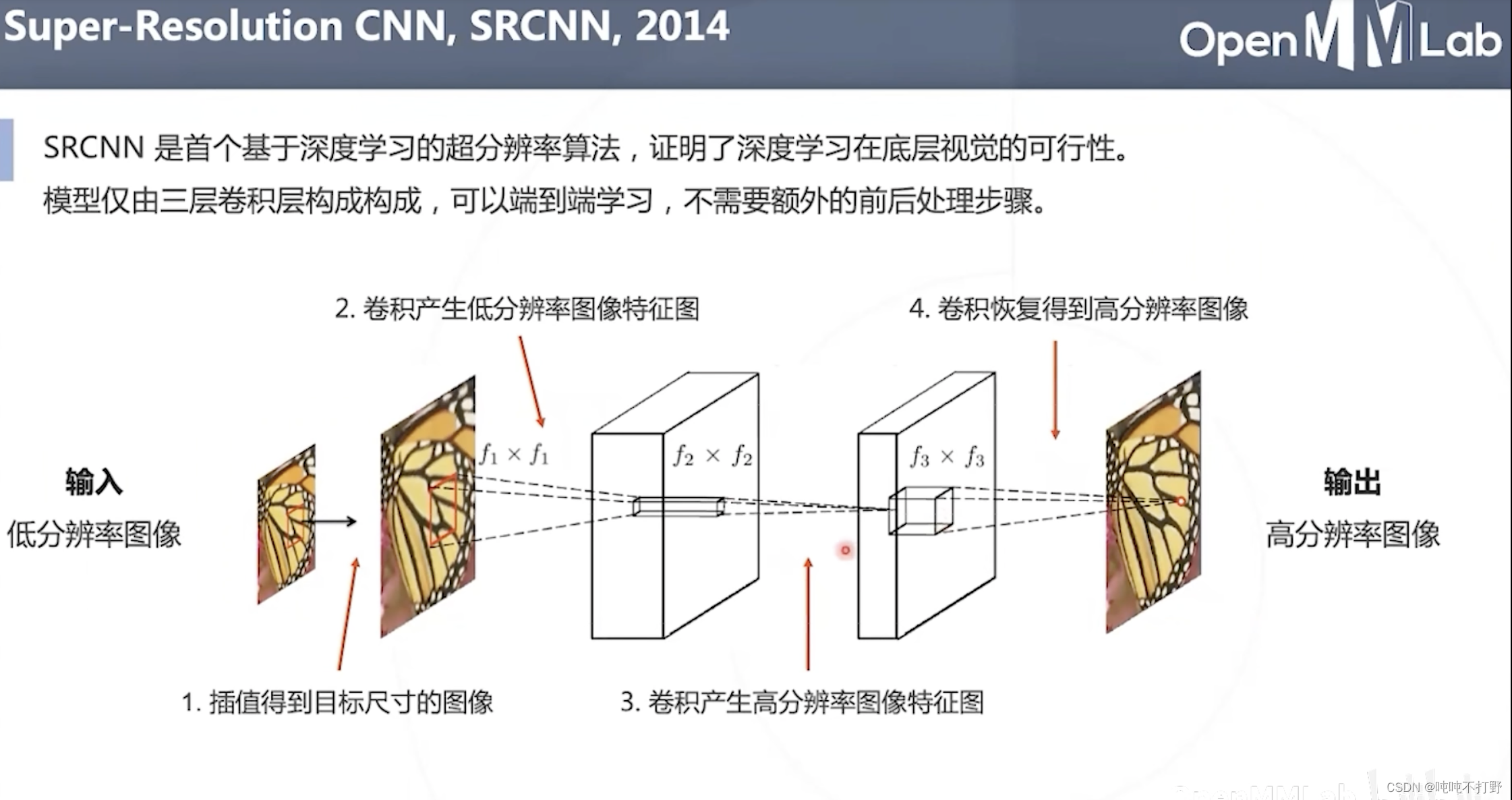
SRCNN(super Resolution CNN,2014年,作者里有Kaiming He),证明了深度学习在底层视觉的可行性。
模型很简单,只有3层卷积:
- 在输入卷积网络之前,先把原始低分辨率图像进行插值,得到目标尺寸(高分辨率对应的尺寸)图像
- 第一层卷积:提取特征
- 第二层卷积:卷积产生高分辨率图像特征(把低分辨率的feature map通过非线性方式映射为高分辨率的表示)
- 第三层卷积:根据空间上的相邻关系把预测组合成最终的高分辨率图像。
- 训练目的就是学习这三层卷积的 f f f,也就是把低分辨率的 Y Y Y,经过 F F F,生成最终的高分辨率 F ( Y ) F(Y) F(Y)
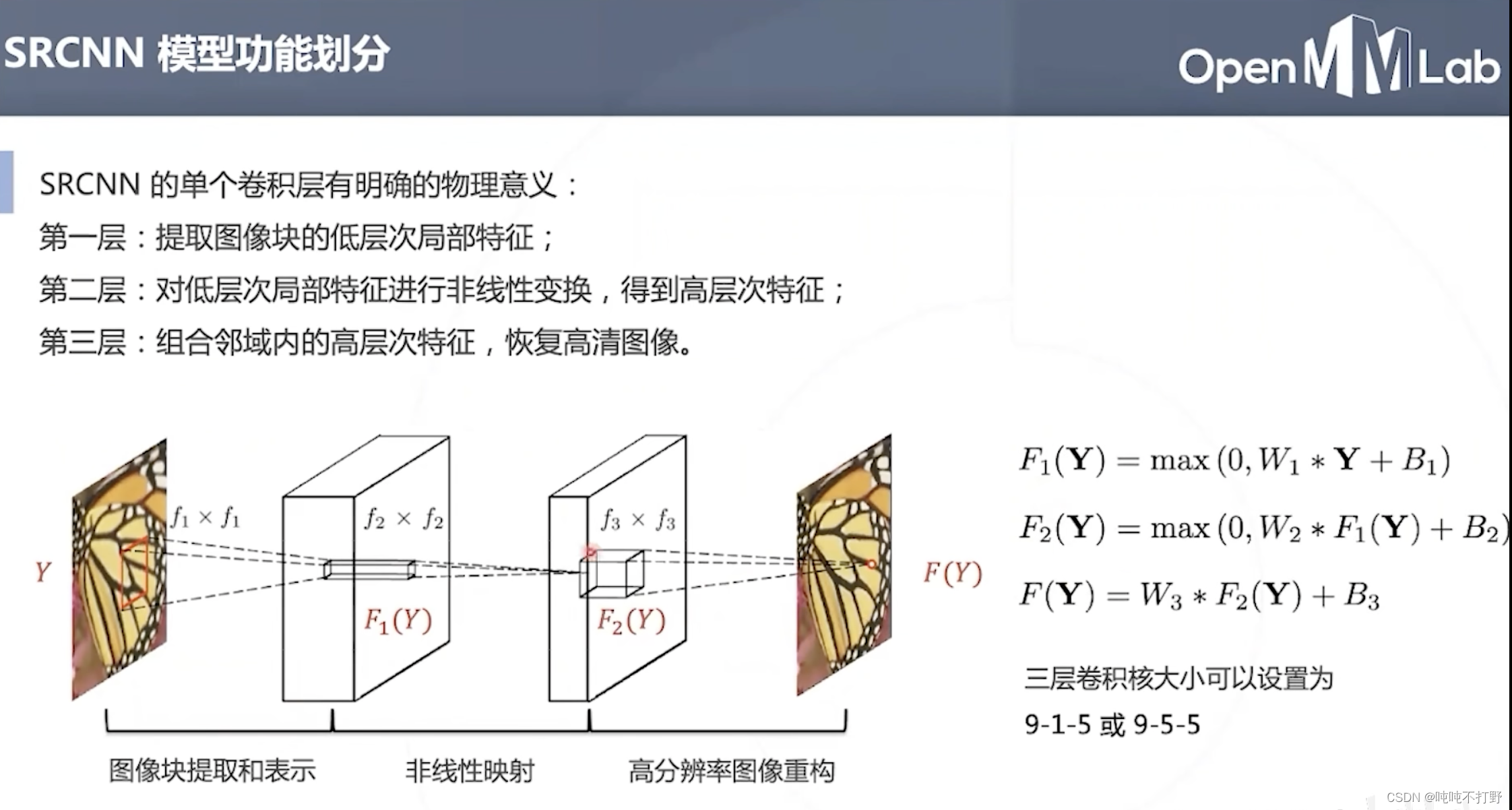
SRCNN的每个卷积层都有明确的物理意义:
- 第一层:提取低分辨率的特征
- 第二层:对低分辨率特征进行变换,得到高分辨率特征
- 这里其实有点像经典的Sparse coding方法中低分辨率字典基底换成高分辨率字典基底的感觉,
- 只是获取那个低分辨率基底的方法不是分解求系数,而是直接用CNN提取特征了
- 另外替换不是保持系数不变,而是用非线性映射了。
- 所以CNN优化和上面sparse coding的优化,后者一定更为复杂吗??
- 第三层:组合邻域内的高分辨率特征,恢复高清图像
可以分别用 F 1 F_1 F1和 F 2 F_2 F2,表示每层的输出特征图的映射, F F F表示卷积神经网络输入到输出的映射
- 不难看出, F 1 F_1 F1和 F 2 F_2 F2这两个卷积层都用的relu激活函数,第三层没有使用激活函数
- 可以看看这篇解读:超分算法之SRCNN
3.1.2 三个卷积层的作用
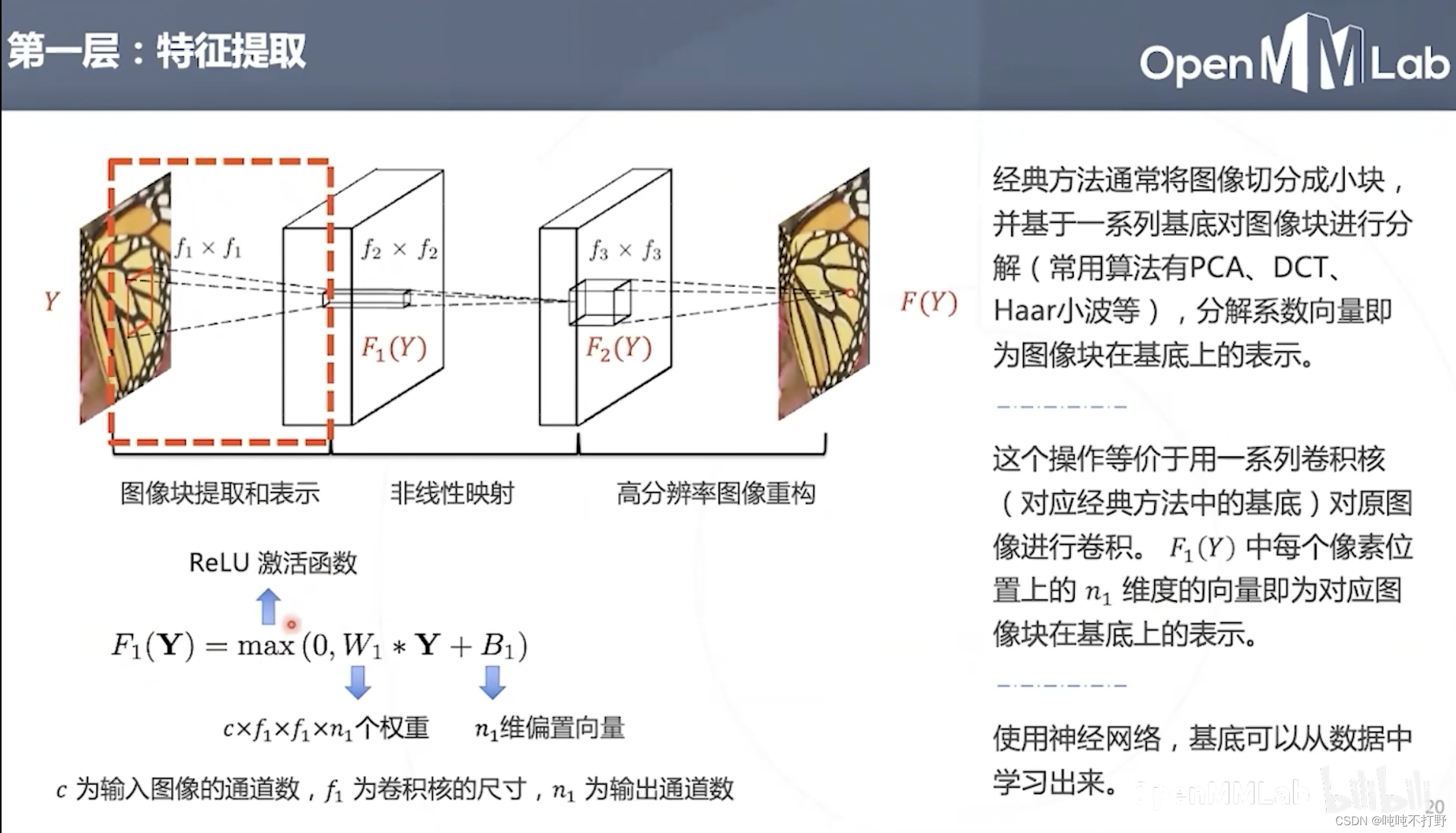
第一层特征提取,relu激活函数,
W
1
W_1
W1就是卷积核,是一个多输出的卷积核,
- 所以其维度: c × f 1 × f 2 × n 1 c\times f_1\times f_2\times n_1 c×f1×f2×n1中,
- c c c是输入通道数, n 1 n_1 n1是输出通道数,卷积后相加的 B 1 B_1 B1,是一个 n 1 n_1 n1维度的向量,即对 F 1 ( Y ) F_1(Y) F1(Y)的特征图的空间分辨率上每一个点(都是 n 1 n_1 n1维度的向量),对应相加。
- 卷积核=Sparse coding中的基图像,
- F 1 ( Y ) F_1(Y) F1(Y)的特征图是 n 1 n_1 n1个通道,特征图上每个像素对应一个 n 1 n_1 n1维度的向量,对应基底向量的系数
- 使用神经网络的好处就是:基底和对应的系数表示可以从数据中端到端的学习出来
关于多输出卷积核,详见:
- 动手学深度学习V2.0(Pytorch)——21. 卷积层里的多输入多输出通道-1.3 多输出卷积部分,
- 图示:相关-21. 卷积的示意图(普通卷积,多通道卷积等)及Featur Map可视化

三个卷积层的卷积核大小可以设置为:9-1-5,或者9-5-5
则对学到的卷积核(9x9大小)进行可视化,可以看到
- 有些是类似于边缘检测的卷积核,有些是纹理检测的卷积核,还有些是类似拉普拉斯/高斯滤波的卷积核
- 下面是原论文里的截图(上采样系数为3)

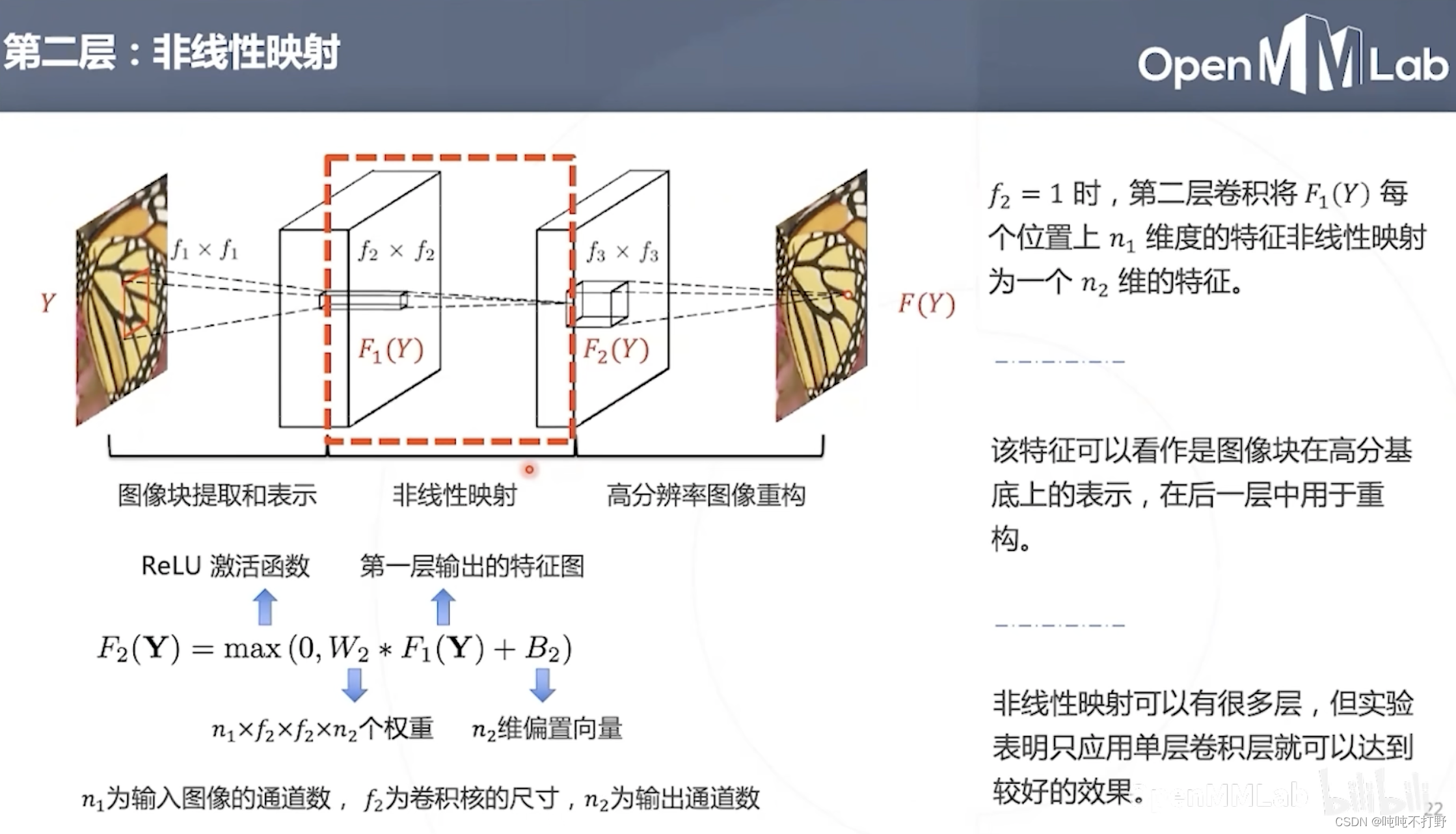
第二层:
- 结构上和第一层很像,也是relu激活函数,也是多输入输出通道。
- 这层的意义是:把低分辨率的基底通过非线性函数映射为高分辨率的基底。
- 这里的非线性映射,有点类似于之前经典稀疏编码方法的系数不变,基底从低换成高
- 非线性映射可以有很多层,不过实验表明,只用单层卷积就可以达到比较好的效果
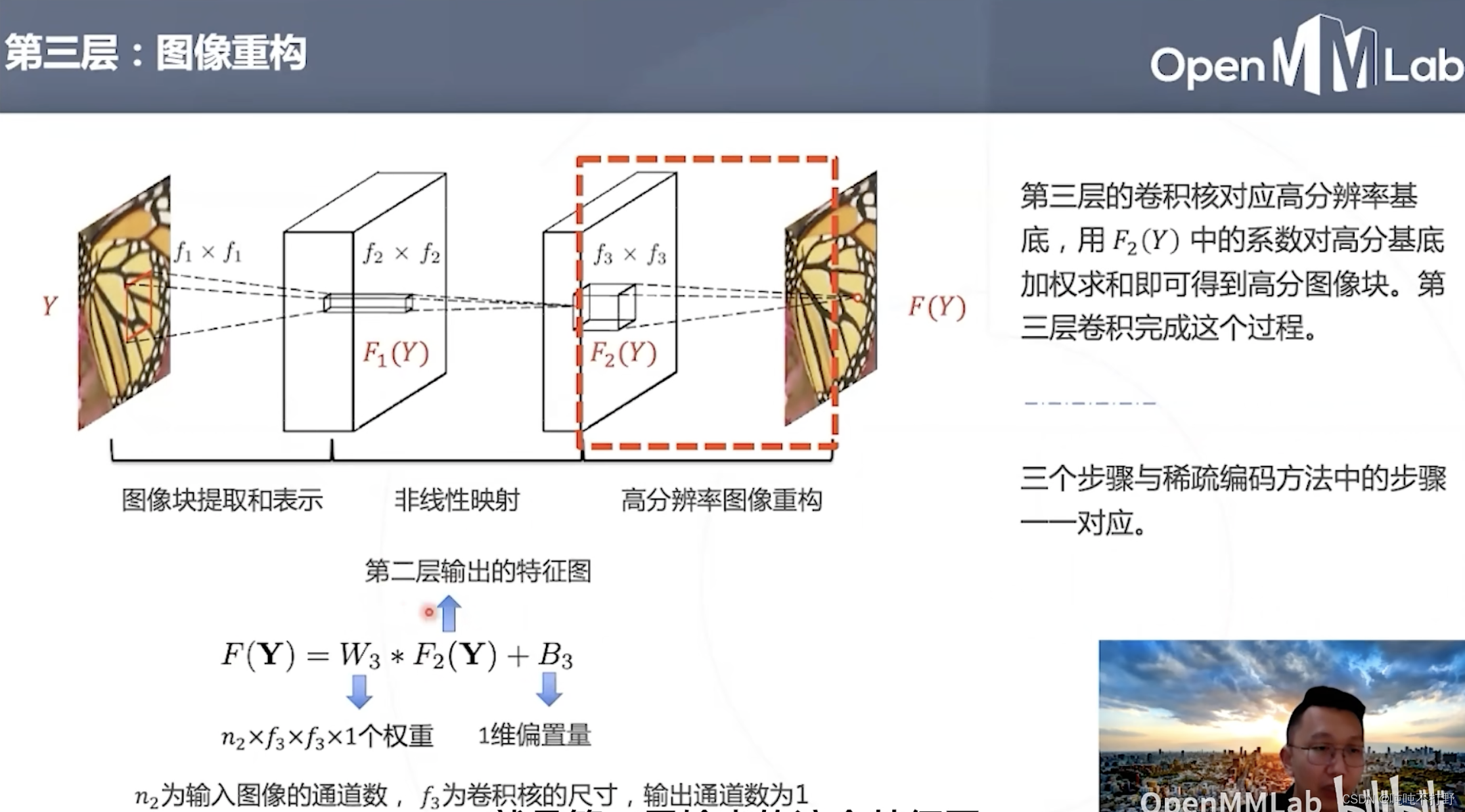
第三层可以看到,是加了个系数(加权求和),第三层其实是获取高分辨率图像对应的基底。
所以整体其实是:
输入(低分辨率图像)
→
\rightarrow
→ 低分辨率的基底(第一个卷积层
f
1
f_1
f1)
→
\rightarrow
→低分辨率基底和高分辨率(第二个卷积层
f
2
f_2
f2)基底映射
←
\leftarrow
←高分辨率的基底(第三个卷积层
f
3
f_3
f3)
→
\rightarrow
→真值(高分辨率图像,输出)
和之前的低分辨率学习低基底,高分辨率学习高基底,其实结构非常类似。
TBD 详情可见下图:
3.1.3 训练和评价

- 数据:高分数据是ImageNet的原图,降采样再插值升采样的图作为低分图像(降采样就会丢失图像的高频信息了,在此基础上就算再升采样也是无法复原的,所以这个作为低分图像是没问题的),只是这种低分图像和实际的低分图像模式会一样吗???数据分布/直方图方面
- 学习参数:要学习的就是三个卷积层的卷积核和偏置
- 损失函数:用最简单的MSE即可
- 优化算法:使用标准的SGD随机梯度下降算法
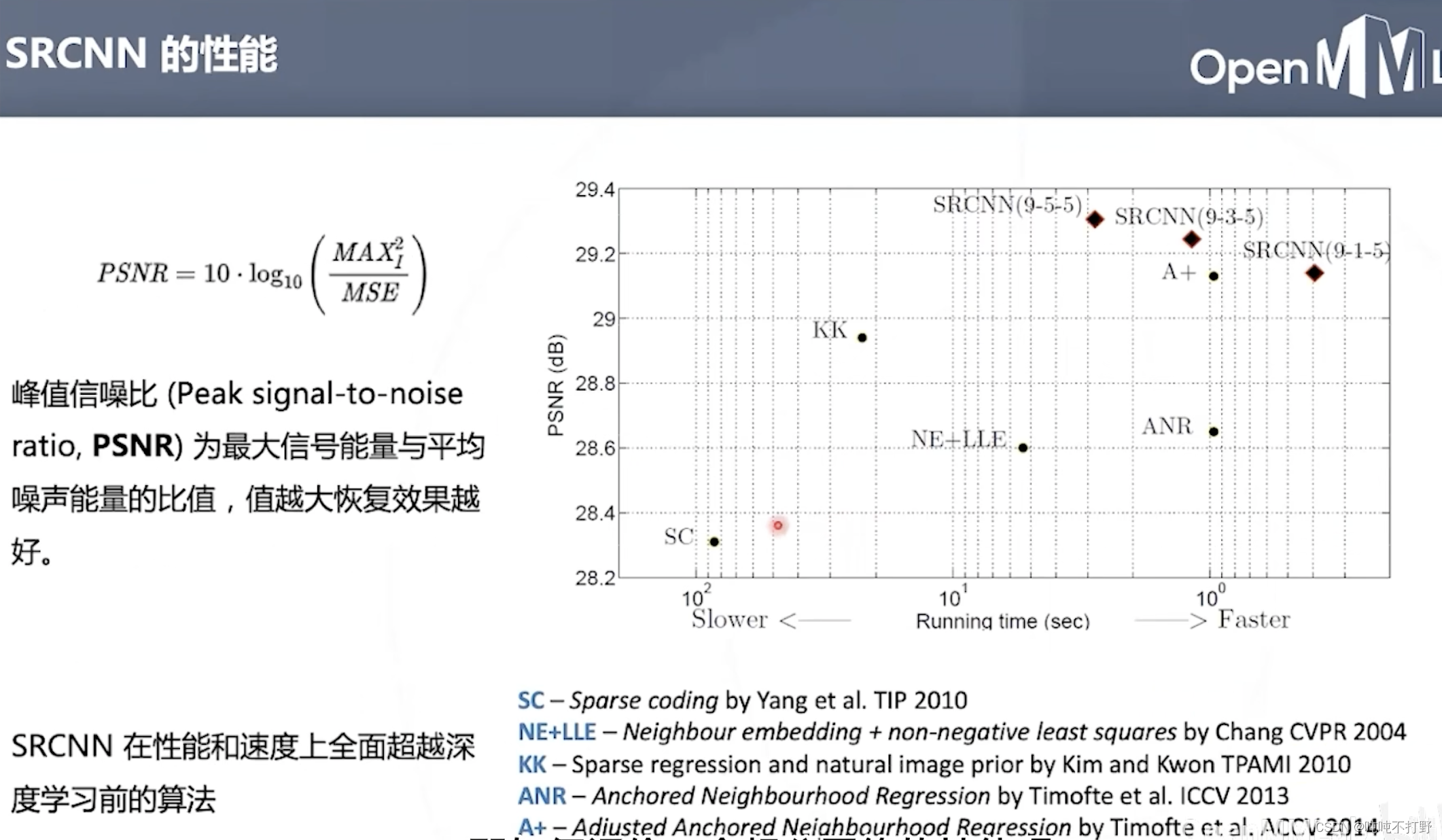
评价指标:PSNR
- 所以卷积核设置,第二层卷积核从9-3-1,精度变化不大,但是时间差距挺大,所以权衡之下,9-1-5的SRCNN就可以了。
- 可以看看百度百科:峰值信噪比
- 之前还有个类似的概念:半峰全宽
3.1.4 效果展示

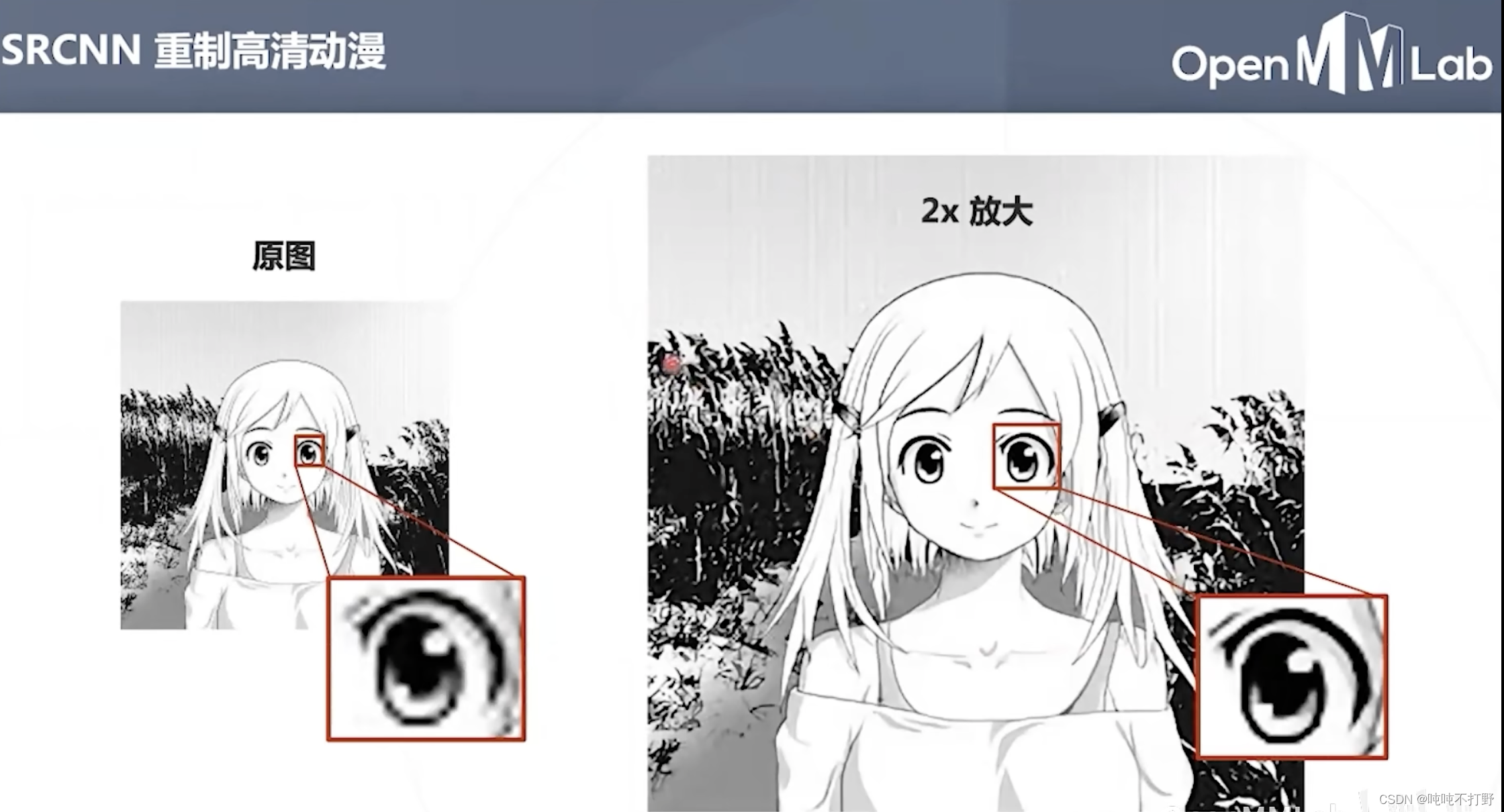
3.1.5 缺点
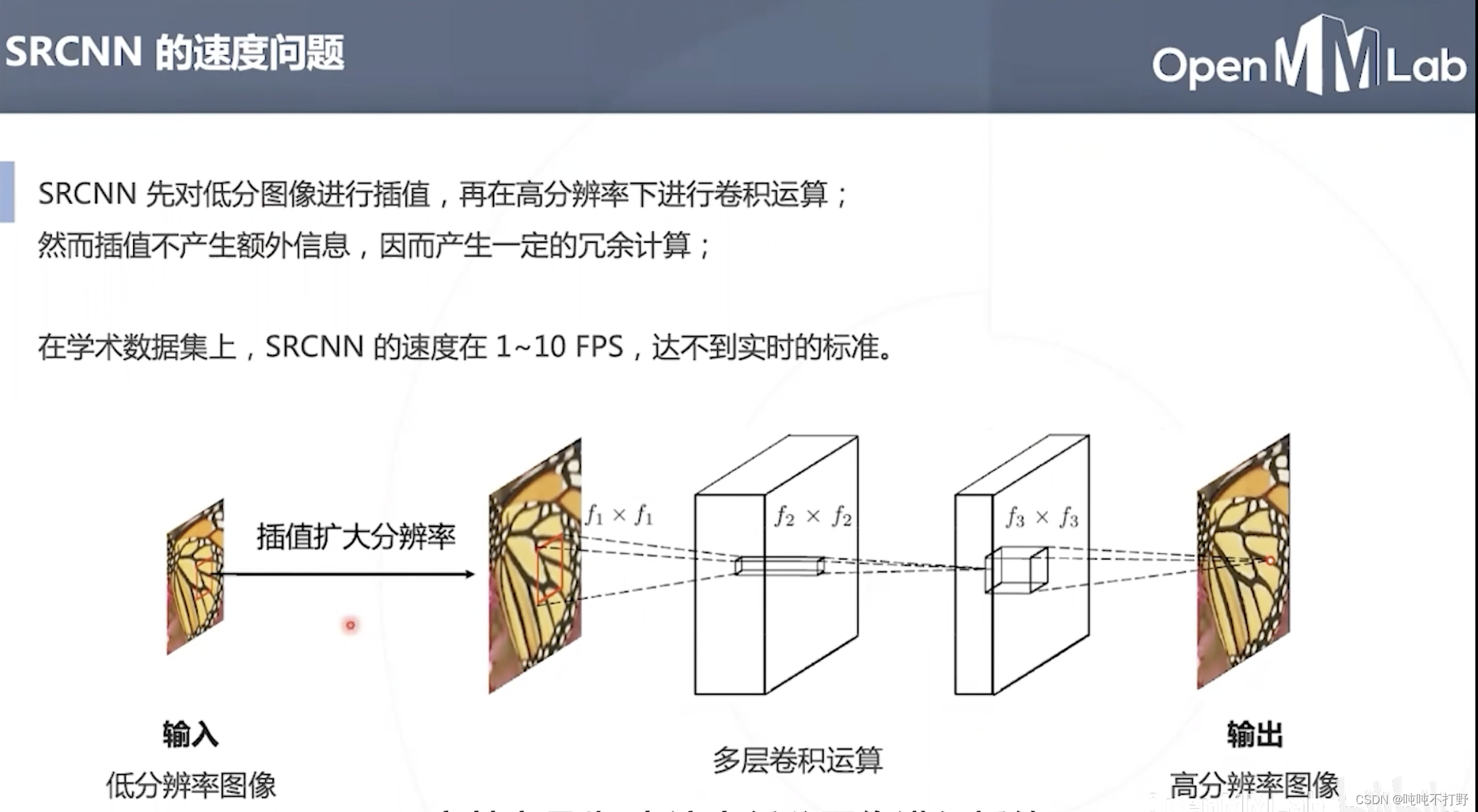
- 在输入卷积网络前,用插值方法扩大分辨率,由于插值并不会引入有用的图像信息,所以这里其实会有一些冗余计算。
- 速度比较慢,每秒1-10张图的处理速度,达不到实时标准。
3.2 FSRCNN(Fast SRCNN2016)
arxiv论文链接:Accelerating the Super-Resolution Convolutional Neural Network

FSRCNN在SRCNN的基础上对速度进行了改进:
- 不使用插值进行预处理,直接在低分辨率图像上完成卷积运算,降低运算量
- 用1x1的卷积层对特征图的通道数进行压缩,进一步降低卷积的运算量
- 若干卷积层后再通过转置卷积(反卷积,上采样)提高图像分辨率
3.2.1 转置卷积
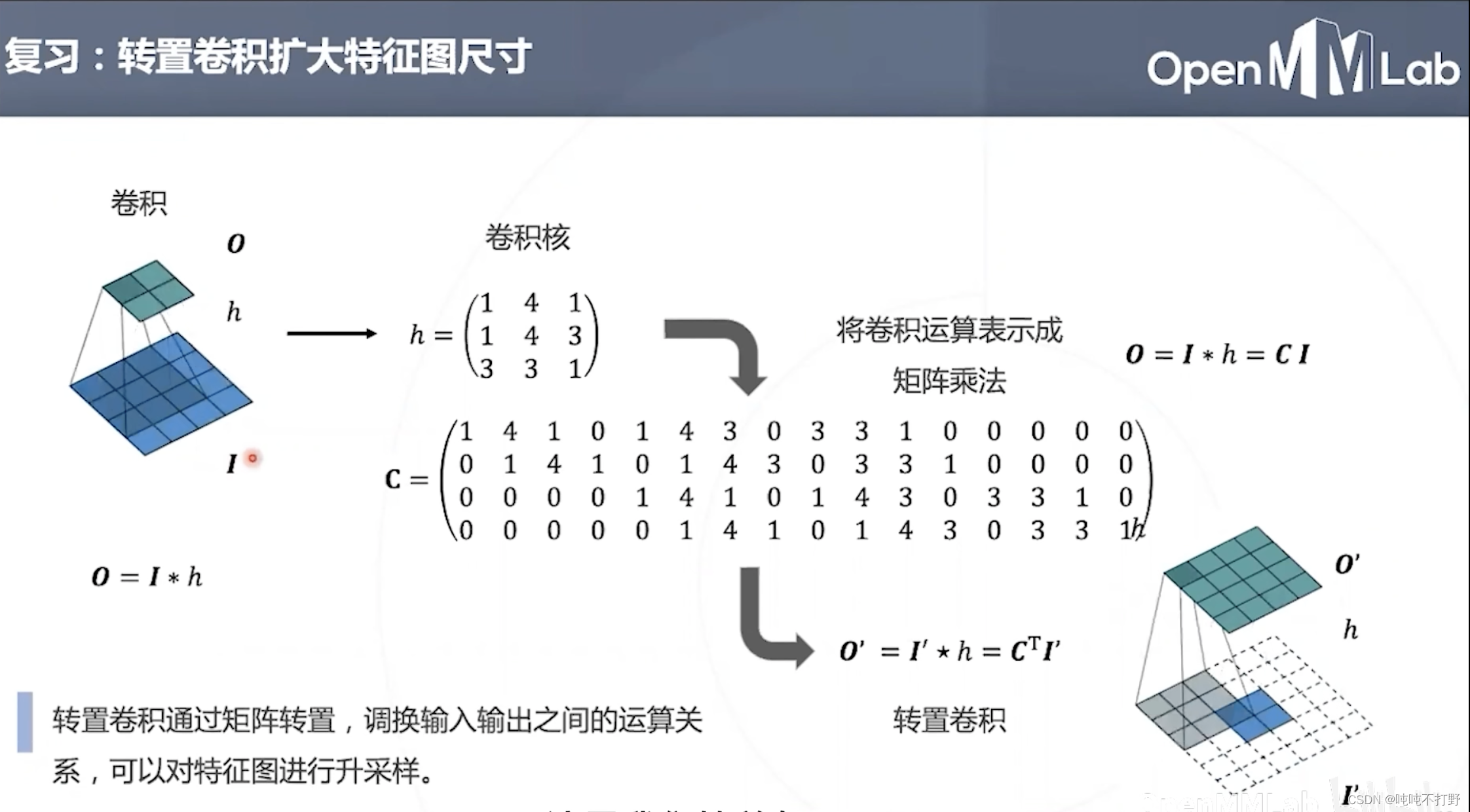
之前在OpenMMLab-AI实战营第二期——5-1.语义分割与MMSegmentation的2.2.1 全卷积网络中提到过,
- 转置卷积(Transposed Convolution),又称为升卷积(Upconvolution),或者反卷积(Deconvolution)
- TBD 系统看一下转置卷积
参考:
- 卷积操作总结(三)—— 转置卷积棋盘效应产生原因及解决,其中卷积操作总结(二)是原理讲解,
- 二中给出了https://github.com/naokishibuya/deep-learning/blob/master/python/transposed_convolution.ipynb
- 以及:https://github.com/vdumoulin/conv_arithmetic,这里有个论文链接: A guide to convolution arithmetic for deep learning
3.2.2 模型
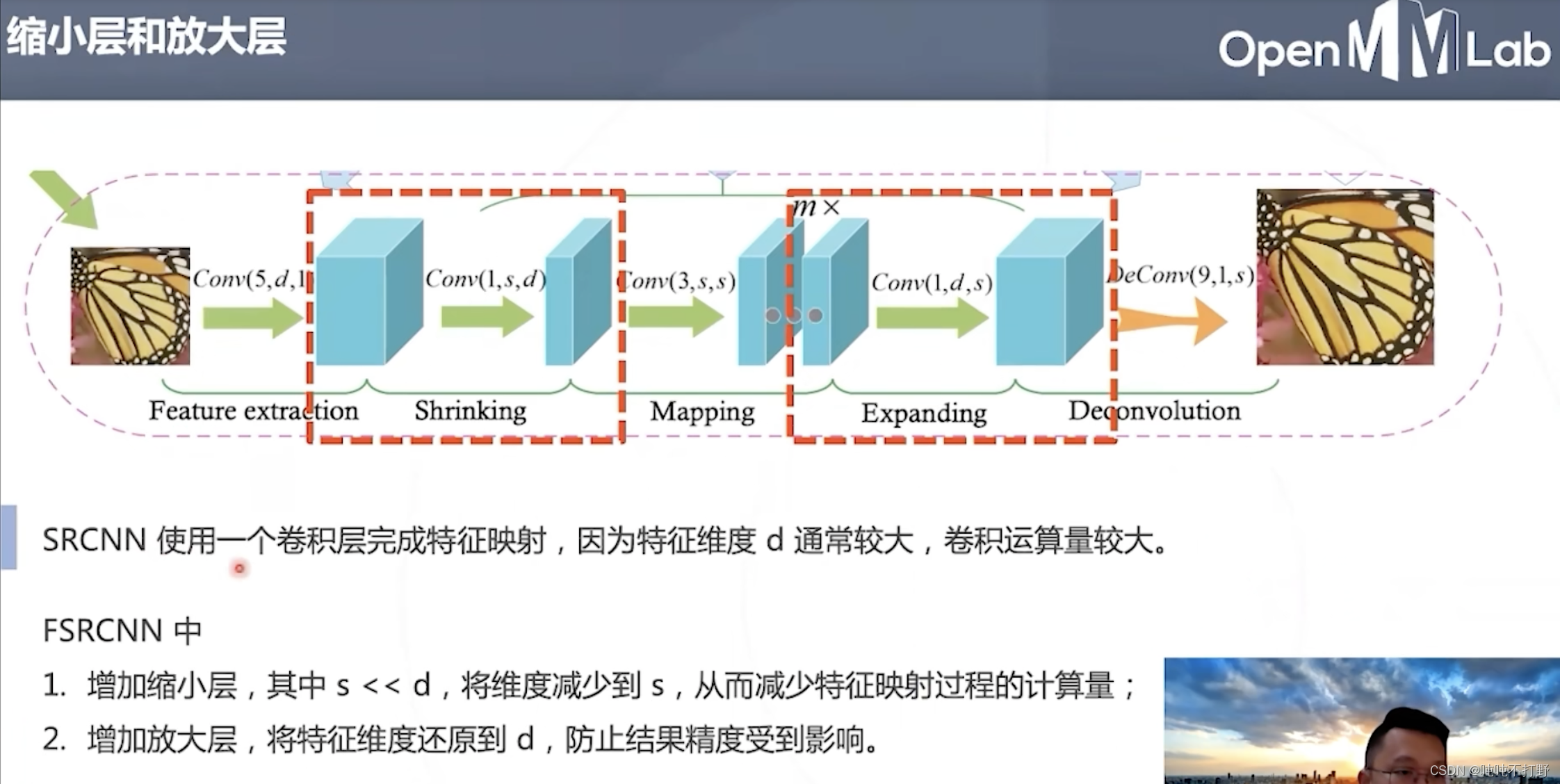
这里是缩小层和放大层,想起之前的SE模块(Squeeze and Extraction),详见:最后一届ImageNet冠军模型:SENet
论文里使用 C o n v ( f i , n i , c i ) Conv(f_i,n_i,c_i) Conv(fi,ni,ci)表示卷积层,其中 f i f_i fi表示卷积核尺寸, n i n_i ni表示卷积核个数, c i c_i ci表示通道数
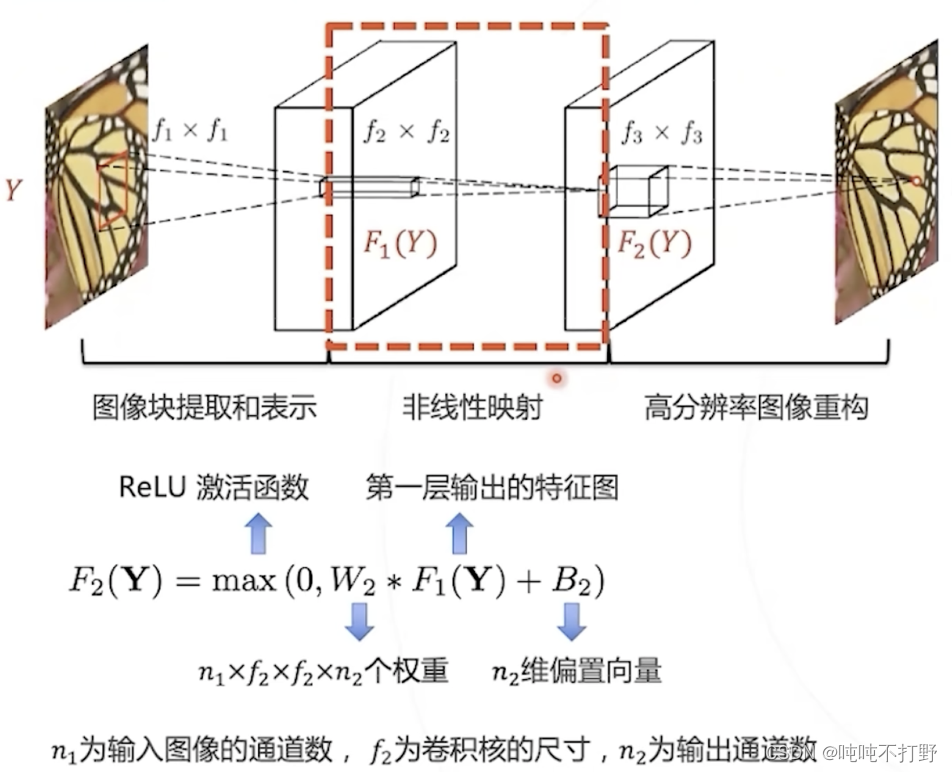
- 在SRCNN中,使用一个卷积层完成特征映射,如下图:(这里
n
1
n_1
n1和
n
2
n_2
n2就是通道数,
n
2
n_2
n2就是上图说的
d
d
d)
- 在FSRCNN中,①增加缩小层(Shrinking),其中s<<d,将维度减少到s,从而减少特征映射过程的计算量;② 增加放大层(Expanding),将特征维度还原到d,防止结果精度受到影响。
- 这也是一种有效的帮助超分模型减少计算量的方式,之前大卷积核变成两个小卷积核,计算量也是减少的,VGG网络的点,详见:动手学深度学习V2.0(Pytorch)——25. 使用块的网络 VGG中4.2 VGG其它讲解部分内容
3.2.3 FSRCNN的优势
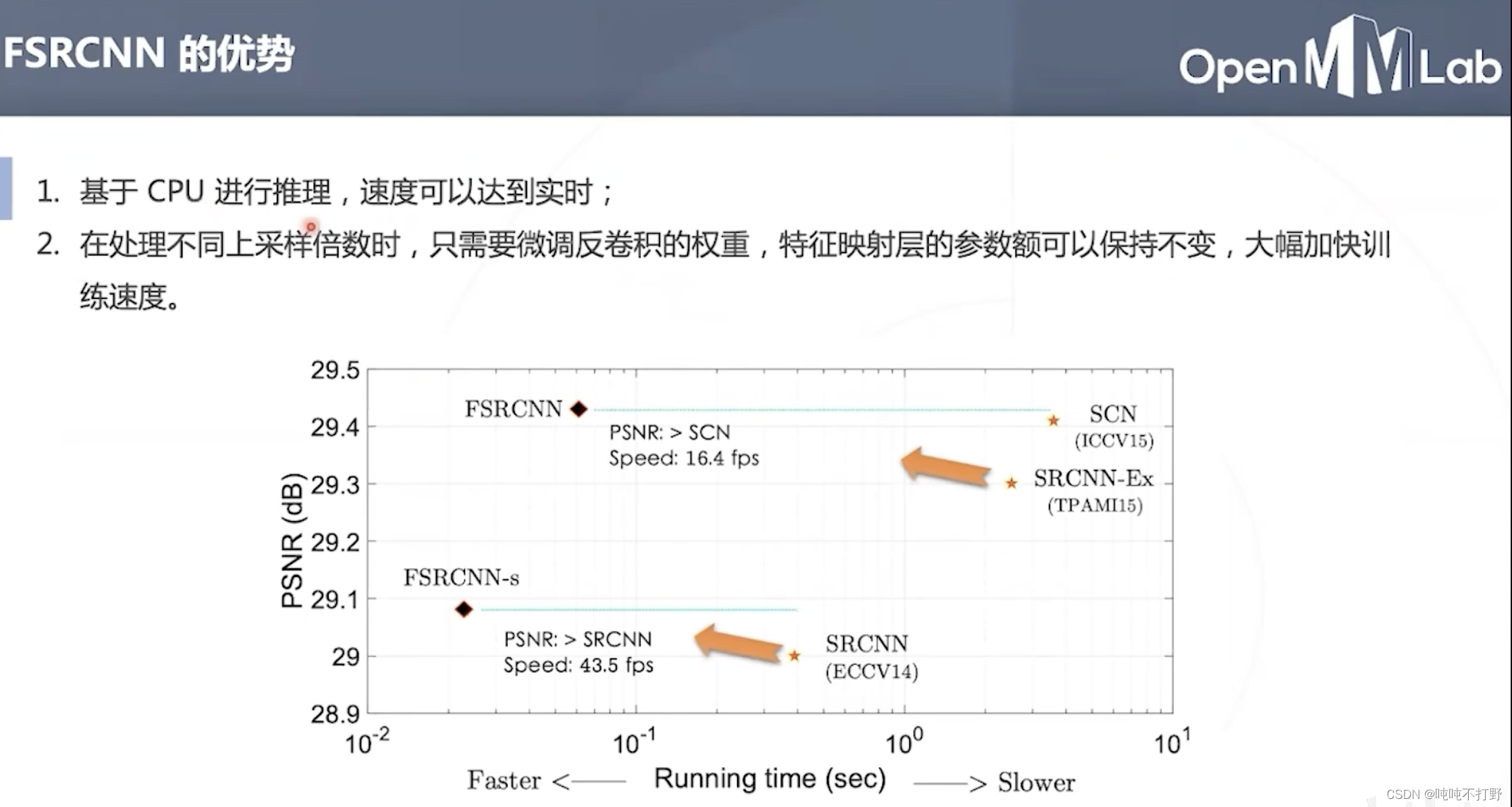
FSRCNN的优势:
- CPU推理已经可以达到实时
- 处理不同上采样倍数时(即低分辨率到超分辨率的分辨率差距),只需要微调反卷积层的权重,特征映射层的参数权重可以保持不变,大幅加快训练速度。就好像目标检测任务可以固定backbone的权重,只调节head部分的权重。
3.2.4 转置卷积的缺陷(FSRCNN的缺陷)
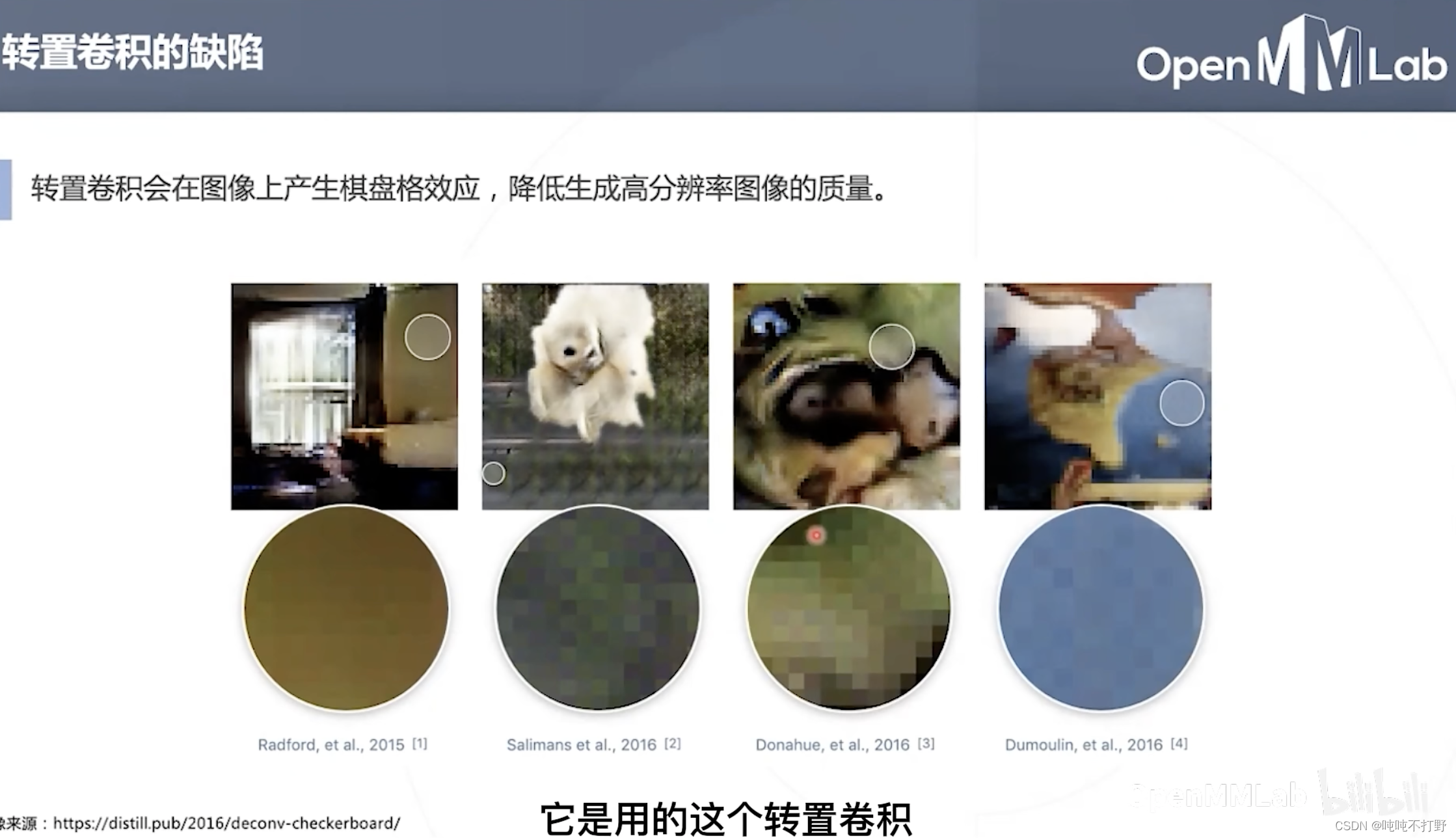
结合3.2.1转置卷积部分的参考去看
- 转置卷积会在图像上产生棋盘格效应,降低生成高分辨率图像的质量
- 而且棋盘格效应,往往会出现在图像上最显著的地方(颜色比较强烈的地方)
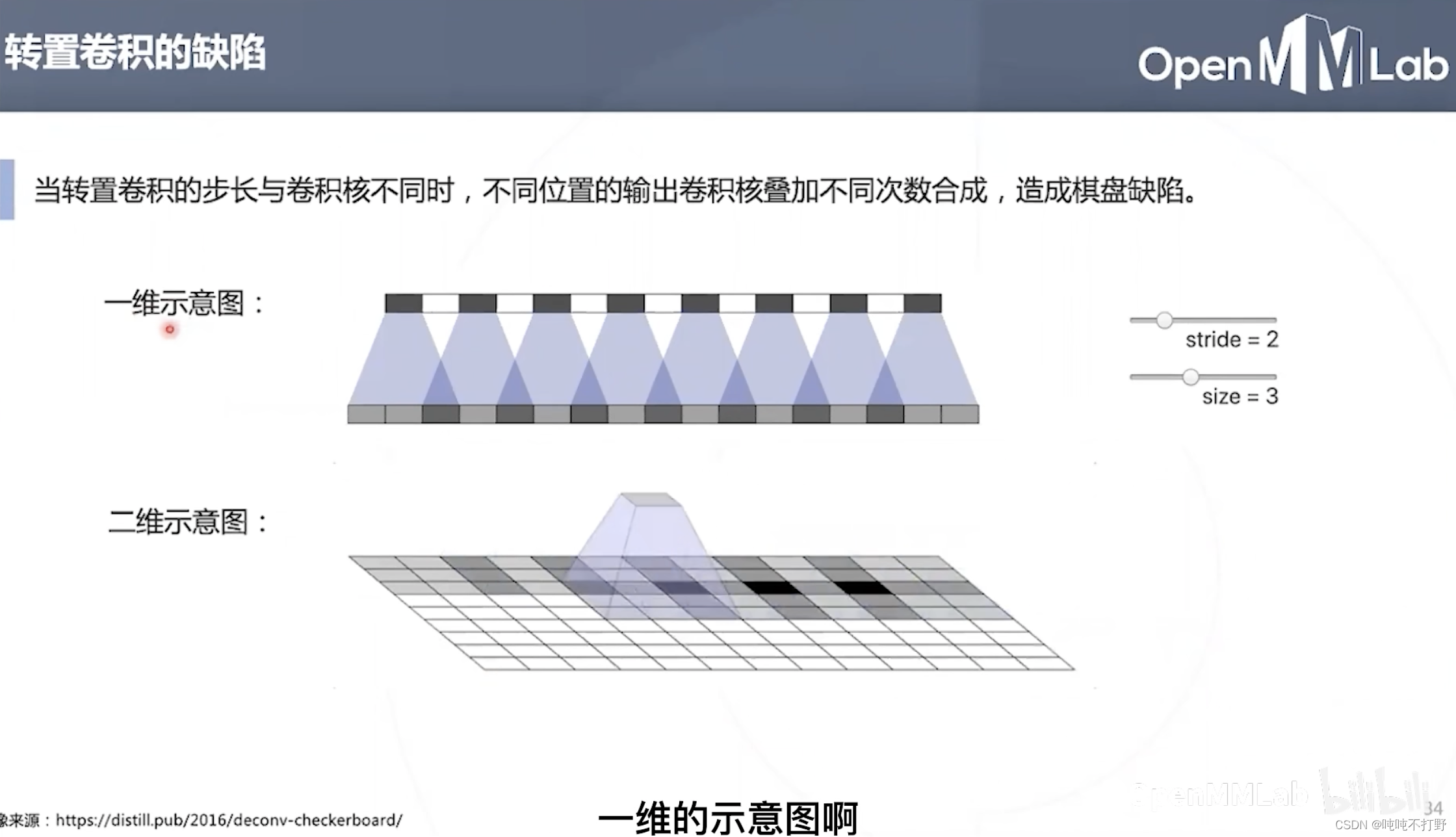
转置卷积会出现棋盘格效应的原因在于:转置卷积的步长,和卷积核不同,导致不同位置输出的卷积核叠加不同次数合成,形成缺陷
如上图:卷积核大小是3,步长是2,则每次计算时都会有。一维和二维都会存在这个情况
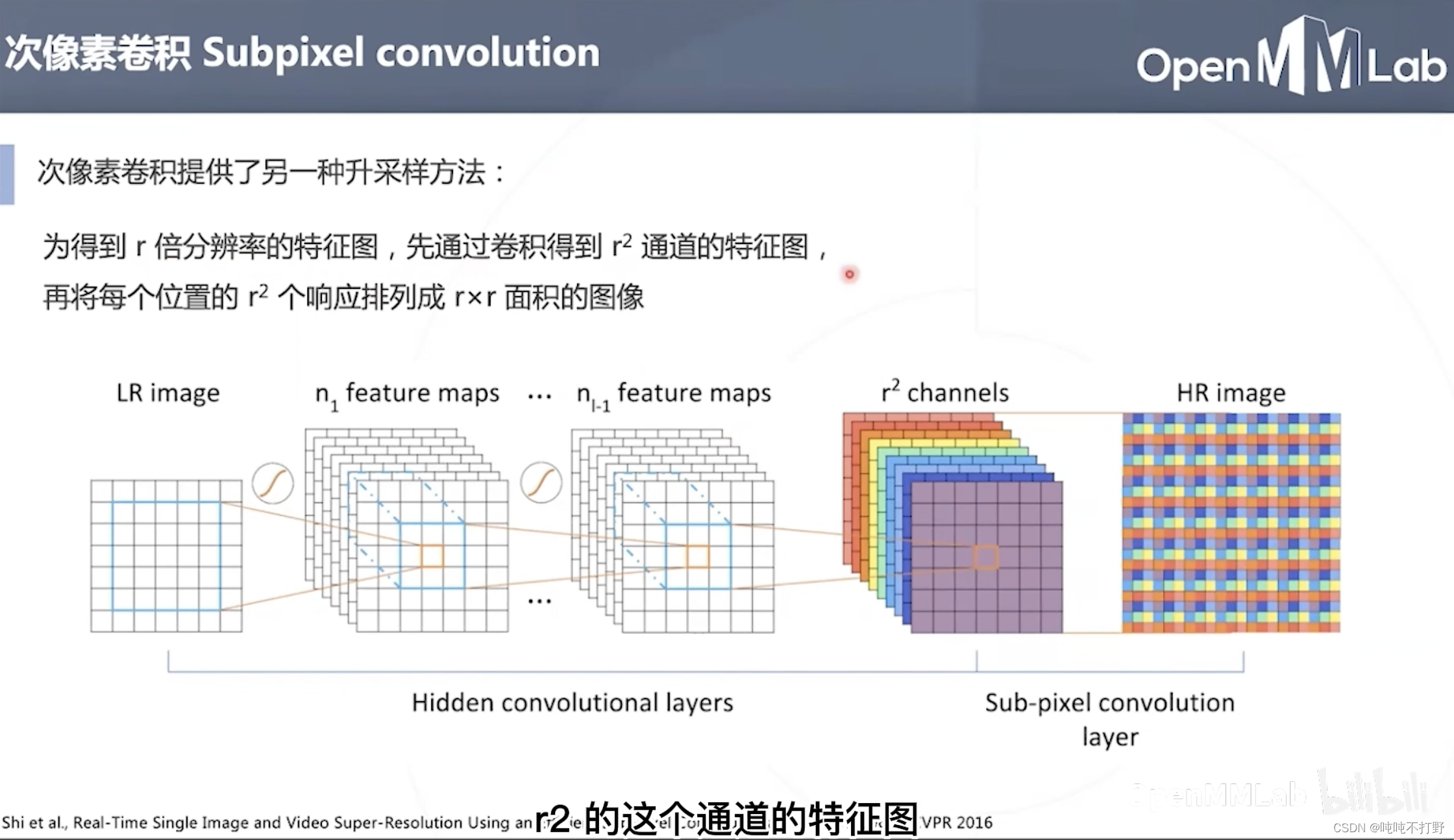
LR Image就是low resolution image,HR 就是 high resolution image。
解决方法转置卷积这个缺陷的方法其实有两种(都是不使用转置卷积,换了别的方式,所以本质上并不是解决转置卷积方法的缺陷,而是找了别的上采样方案):
- 利用插值进行上采样,在插值后的图像上进行卷积(这不就又回到老路上了。。)
- 次像素卷积:
- 如果想得到r倍分辨率的特征图,先通过卷积得到 r 2 r^2 r2通道的特征图
- 再将每个位置的 r 2 r^2 r2个响应排列成 r × r r\times r r×r面积的图像
3.2.5 SRResNet2016(使用resnet和次像素卷积)
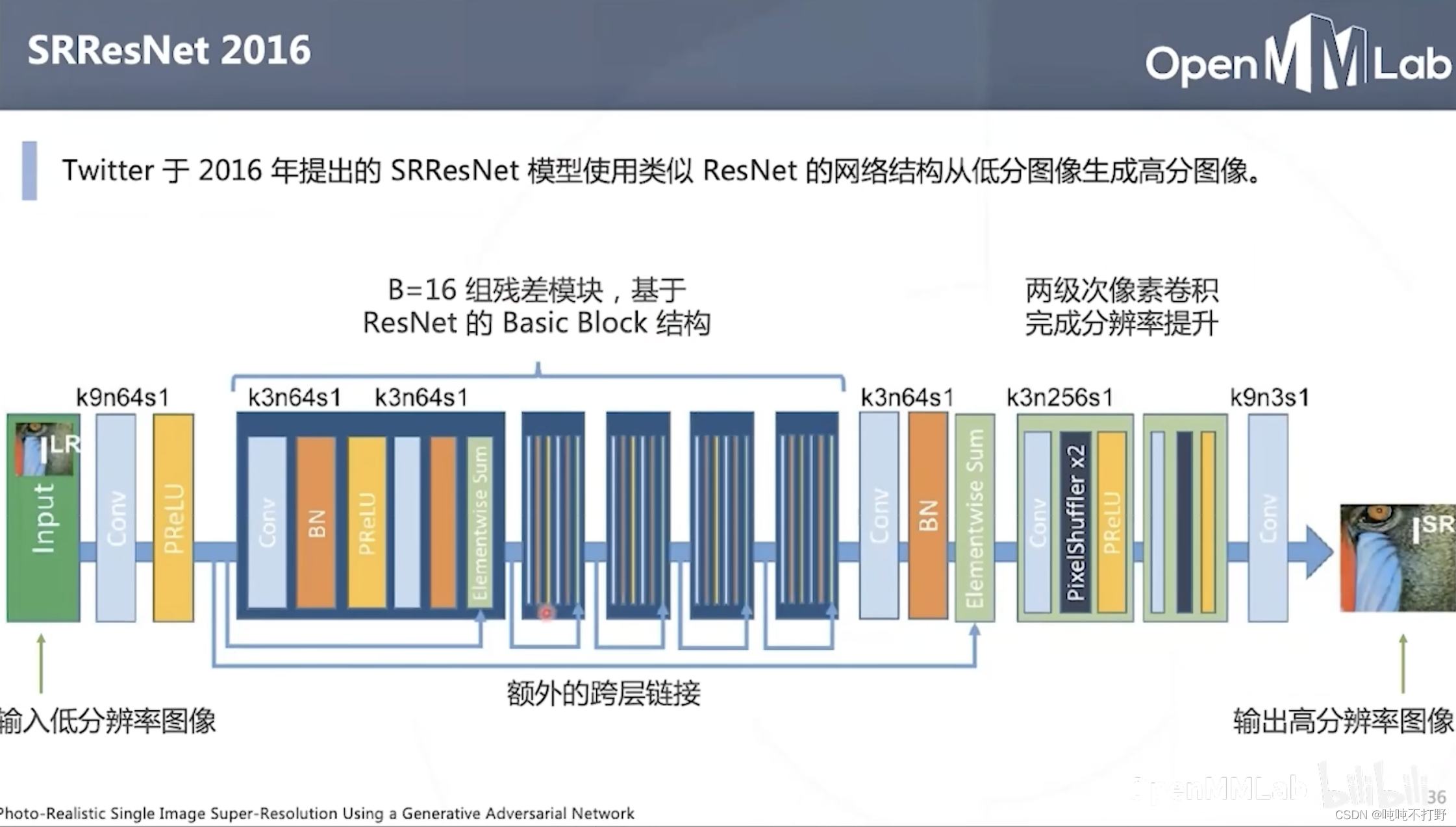
3.3 损失函数

逐像素计算的损失函数,这个比较常见。
感知损失函数,可以看看
- 【论文精读】AI滤镜前置科技树-感知损失函数 Perception Loss
- 损失函数——感知损失(Perceptual Loss)
3.3.1 均方误差
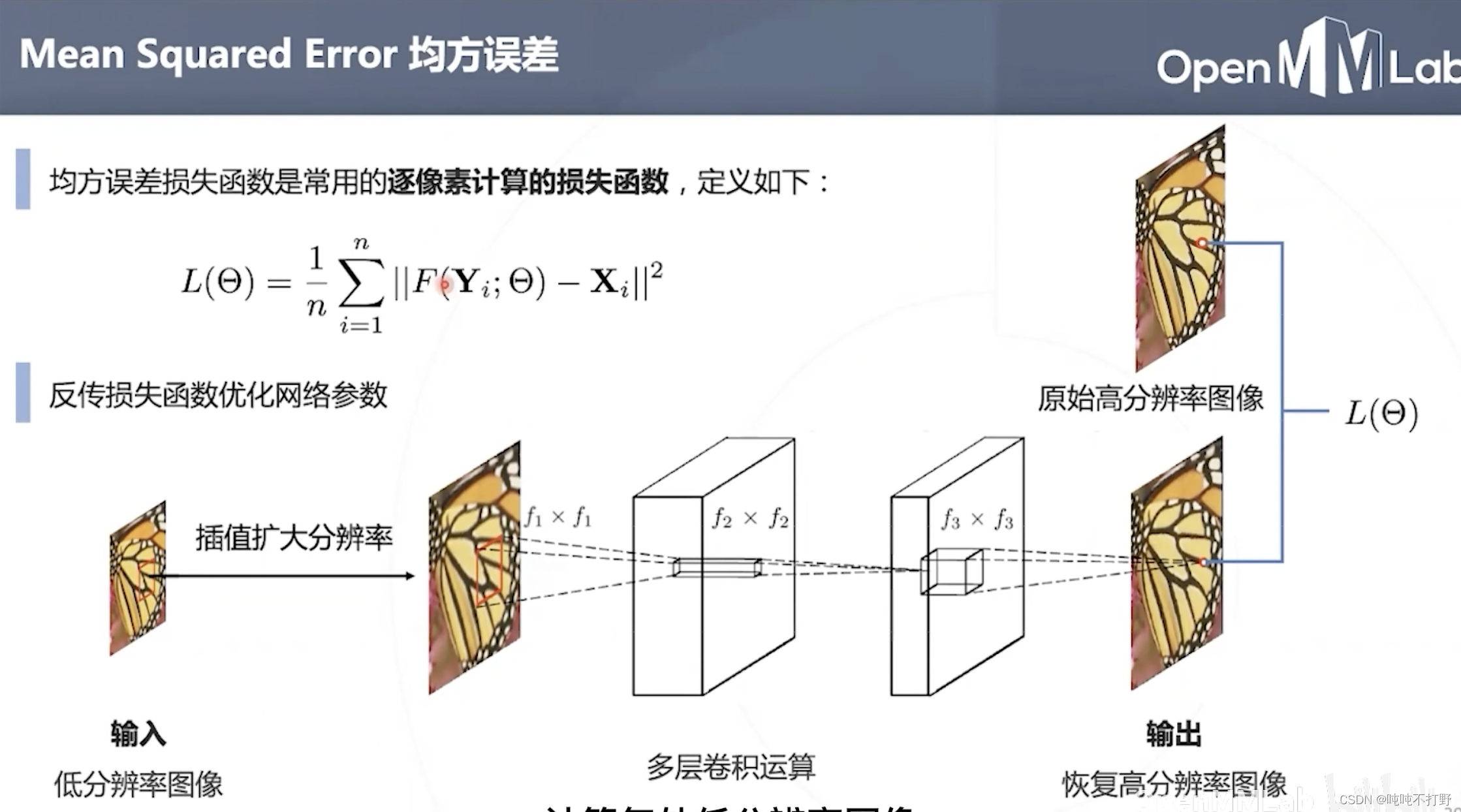
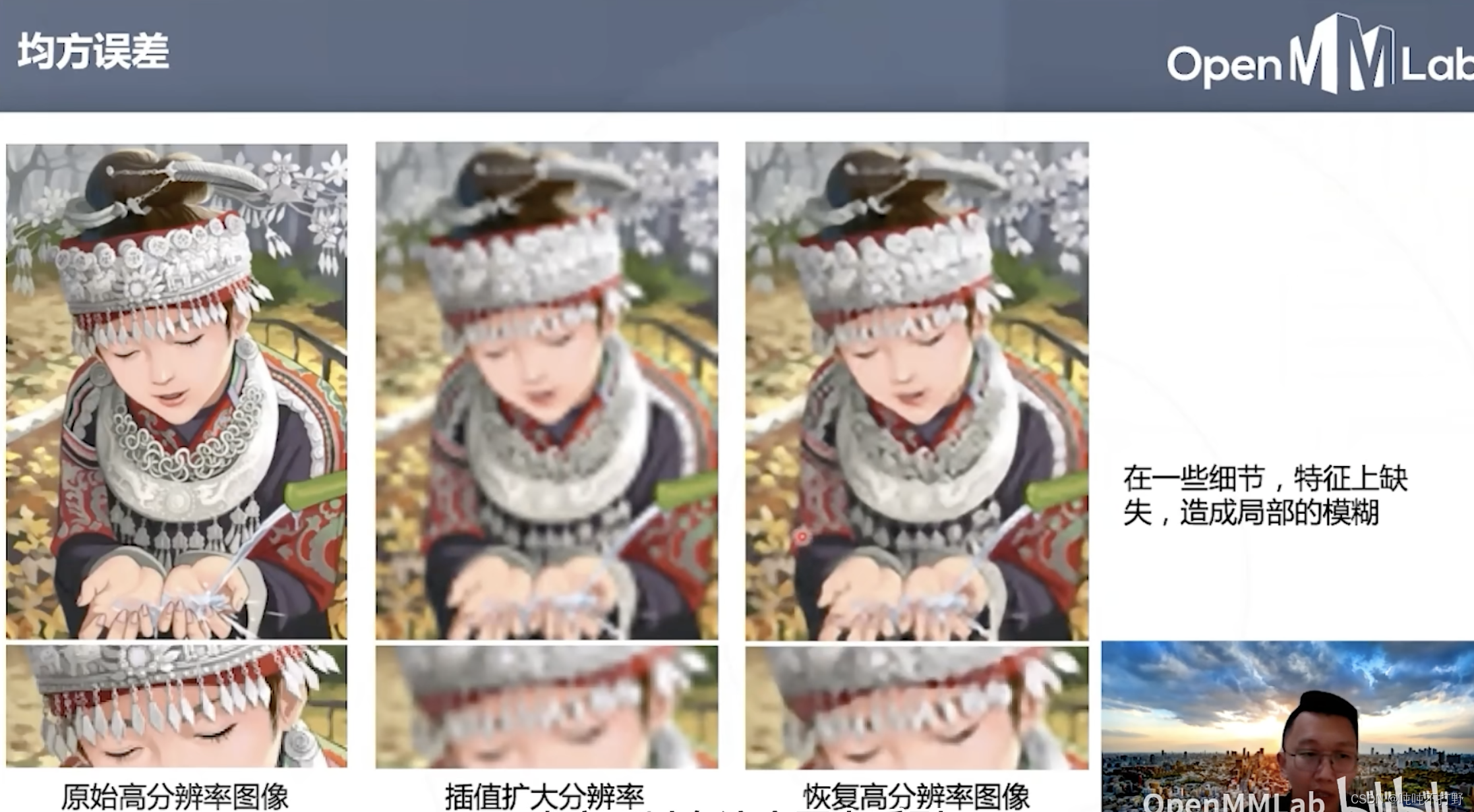
使用均方误差作为损失函数,在一些细节,特征上缺失,会有局部的模糊
3.3.2 感知损失
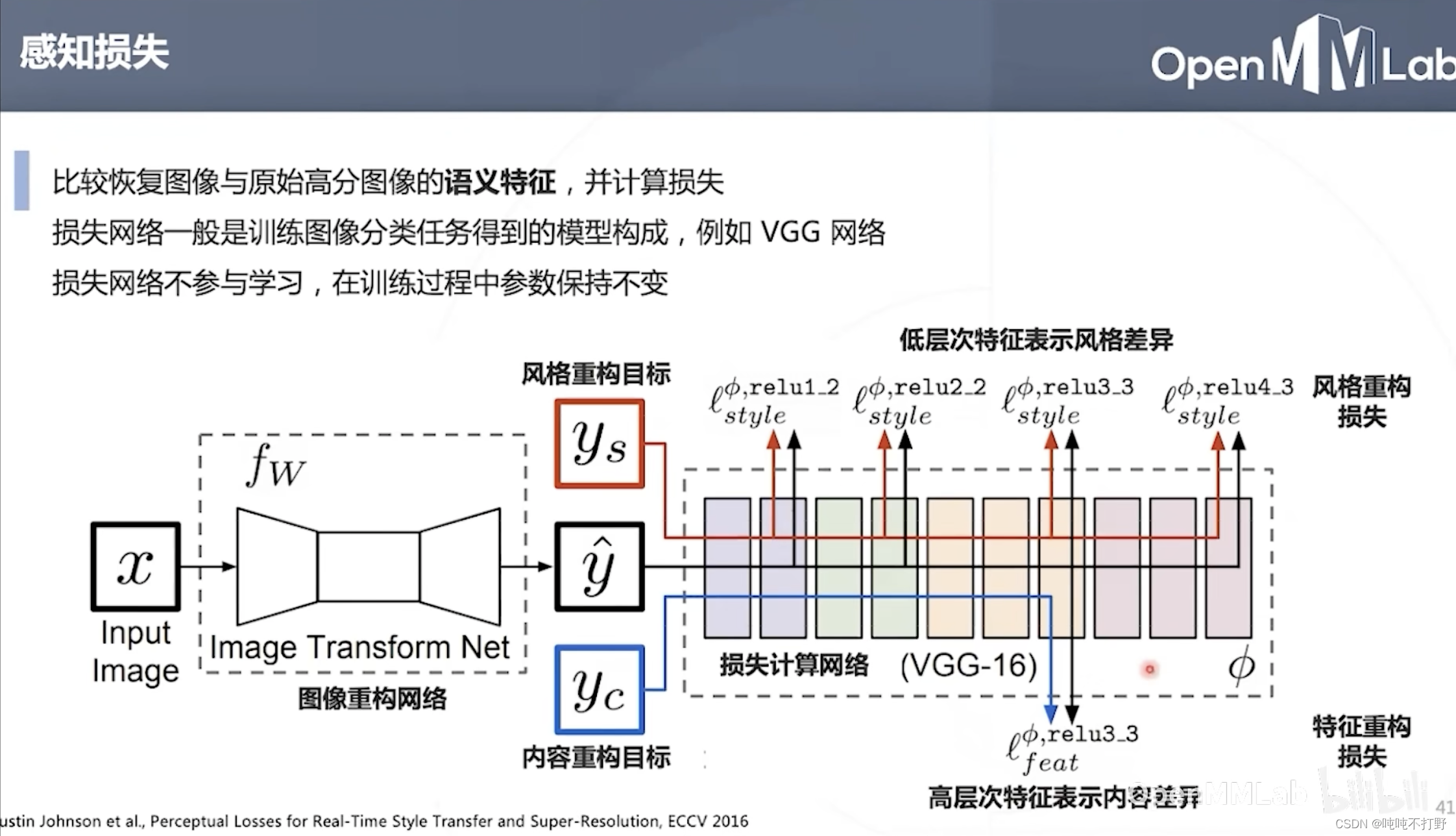
因此2016年,李飞飞团队提出了感知损失。
- 用一个预训练模型,一般是训练分类任务得到的模型,比如Imagenet上训练的VGG网络。
- 这里只需要看 y ^ \hat y y^和 y c y_c yc比较,要的是哪个特征重构损失。
- 训练期间这个损失计算网络的参数不会改变,不参与梯度更新
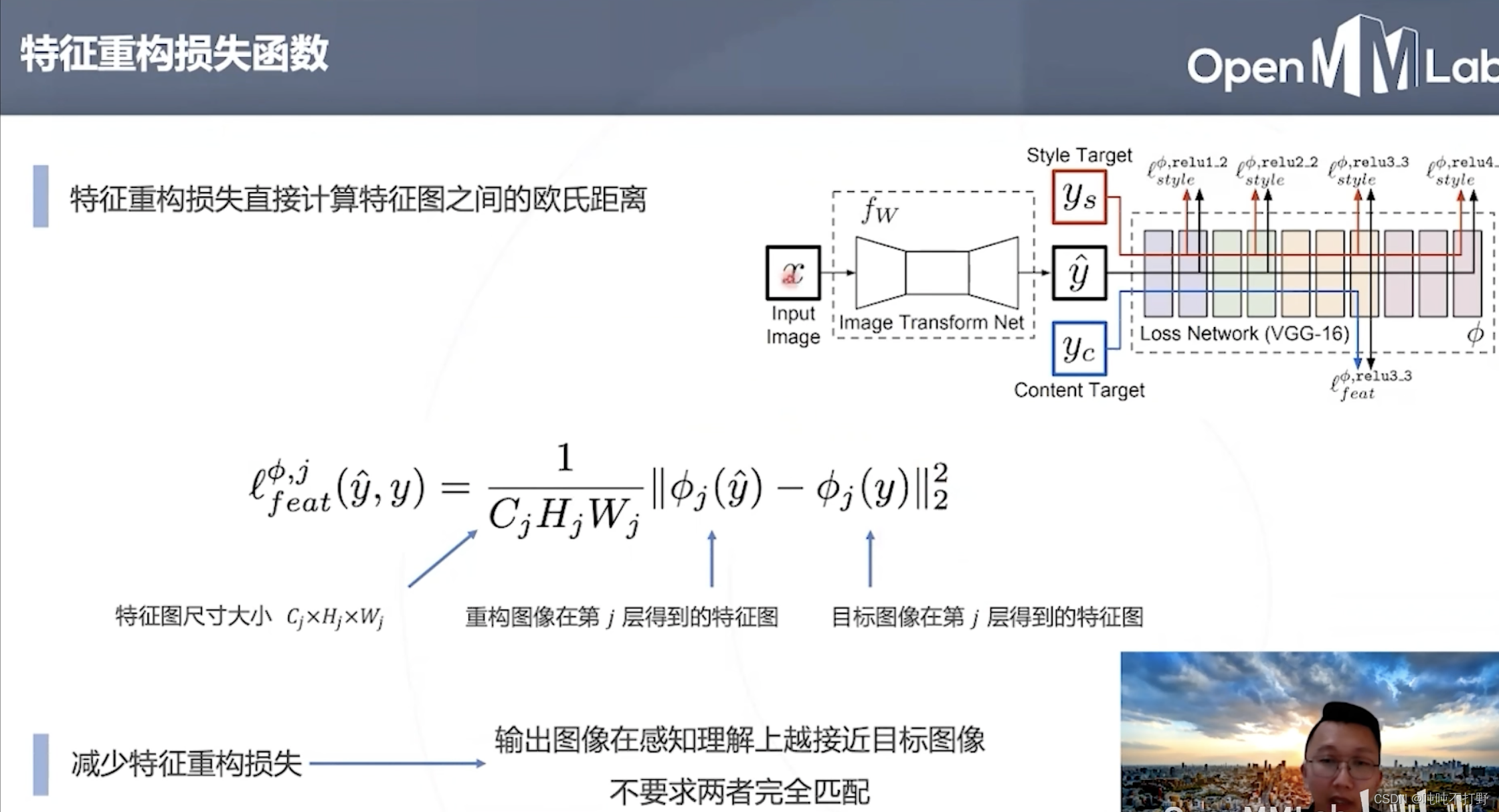
特征重构损失函数:直接计算特征图之间的欧式距离,对应特征图的对应位置相减
- 使用这个损失函数,可以减少特征重构损失,
- 让模型朝着感知理解的方向去接近目标图像,而不是在像素值上完全匹配,即让输出图像在感知理解上接近目标图像(让重构出的图像更真实,细节更丰富)

现在的超分网络都使用了均方误差和感知损失,可以看到,感知损失恢复的高分辨率图像保留了更多的细节
3.4 对抗生成网络GAN简介
GAN(generateive adversarial network)是一种无监督的网络,在超分任务上有广泛的应用。
3.4.1 概念
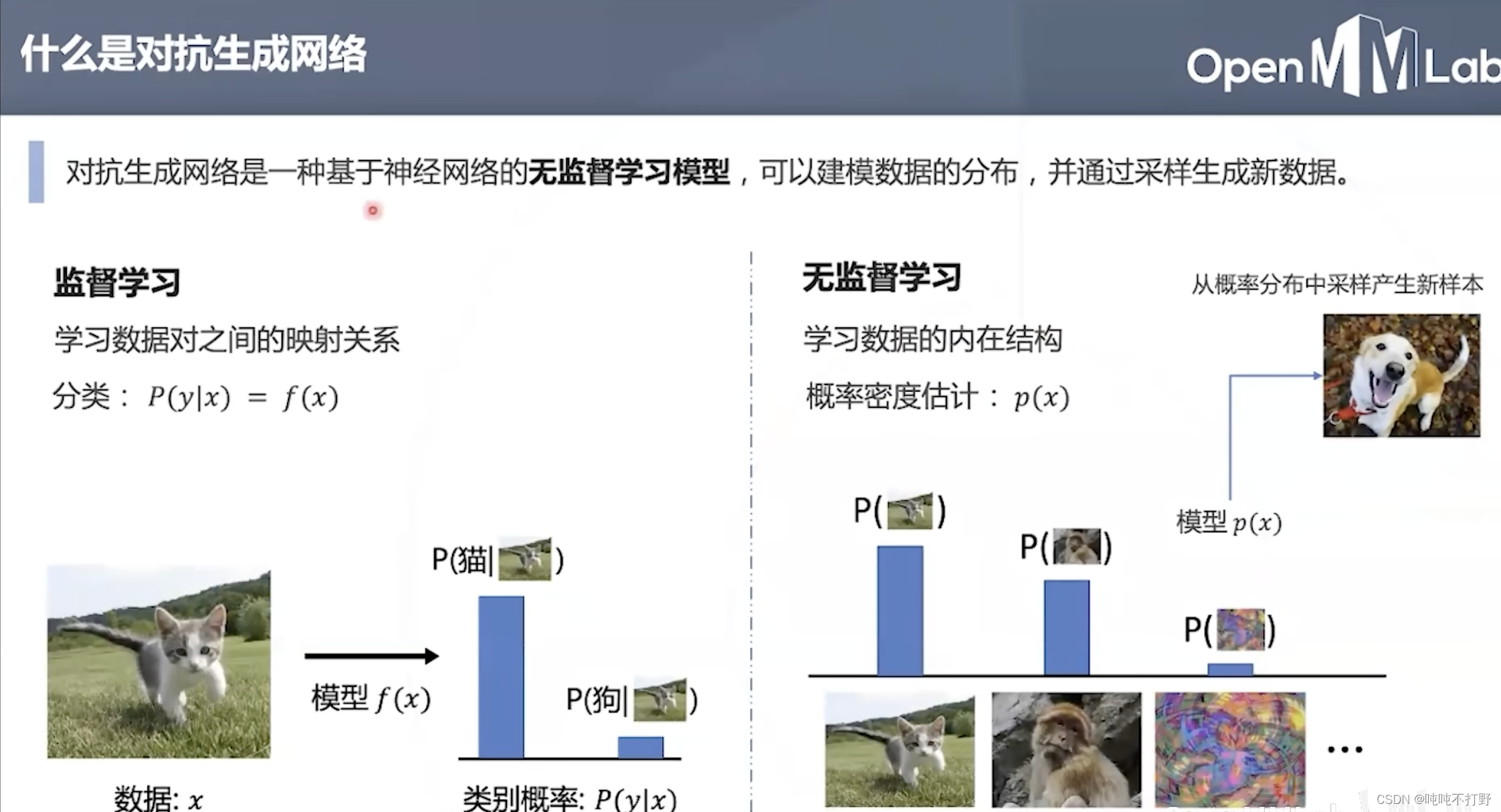
- 监督学习学的其实是:输入输出这种数据对之间的映射关系
- 无监督学习学的其实是:数据的内在结构(内在关联,比如数据分布等,一般可以认为是学习一个概率密度估计, p ( x ) p(x) p(x))
3.4.2 应用
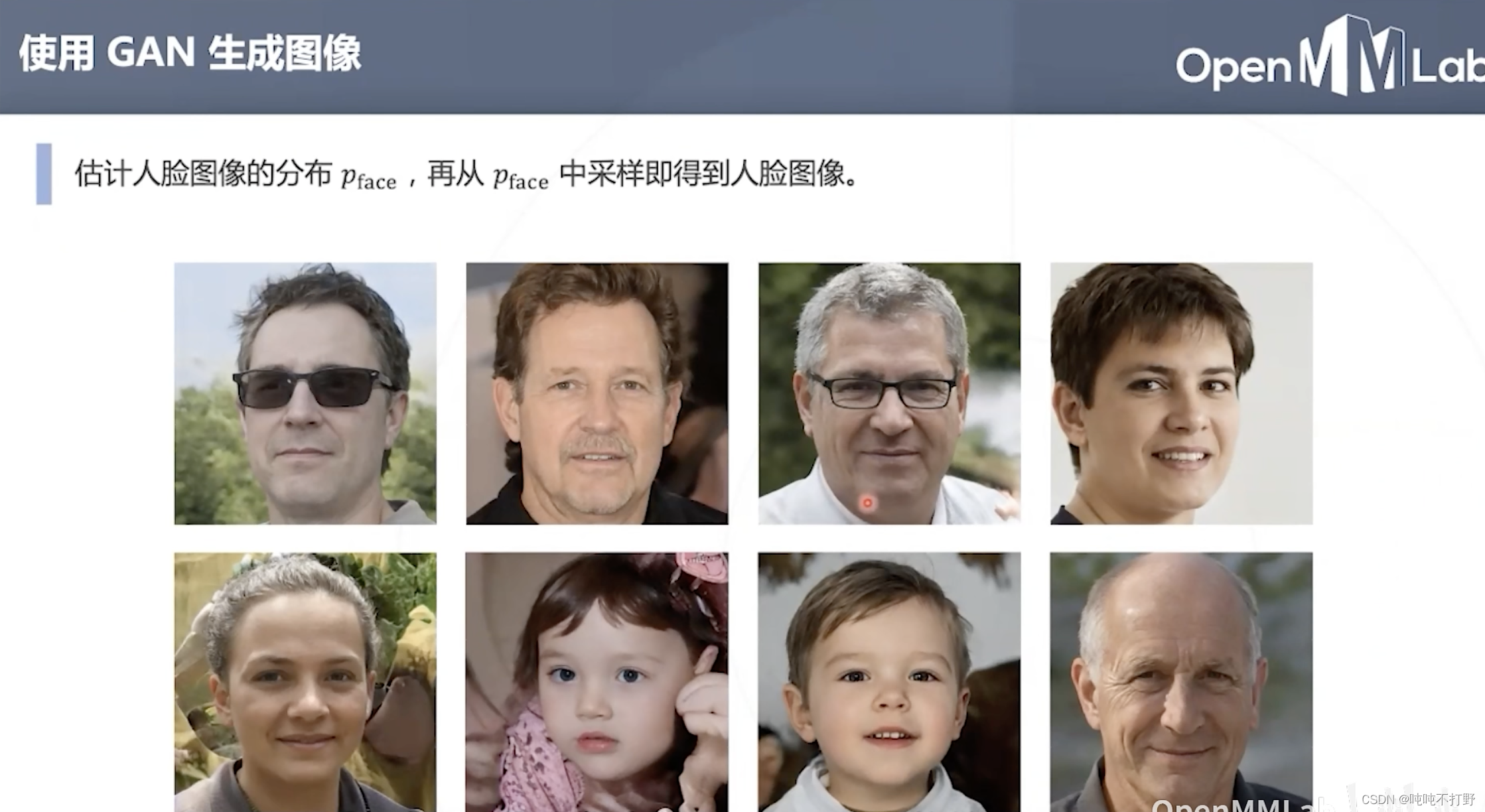
用GAN拟合人脸的数据分布,再从分布中采样,就可以得到这些看起来非常真实的图像

利用GAN转译图像

以及用GAN进行超分任务,图三和图二相比,SRGAN的细节是优于SRResNet的(图四是原图)
3.4.3 用神经网络表示和学习数据分布(GAN)
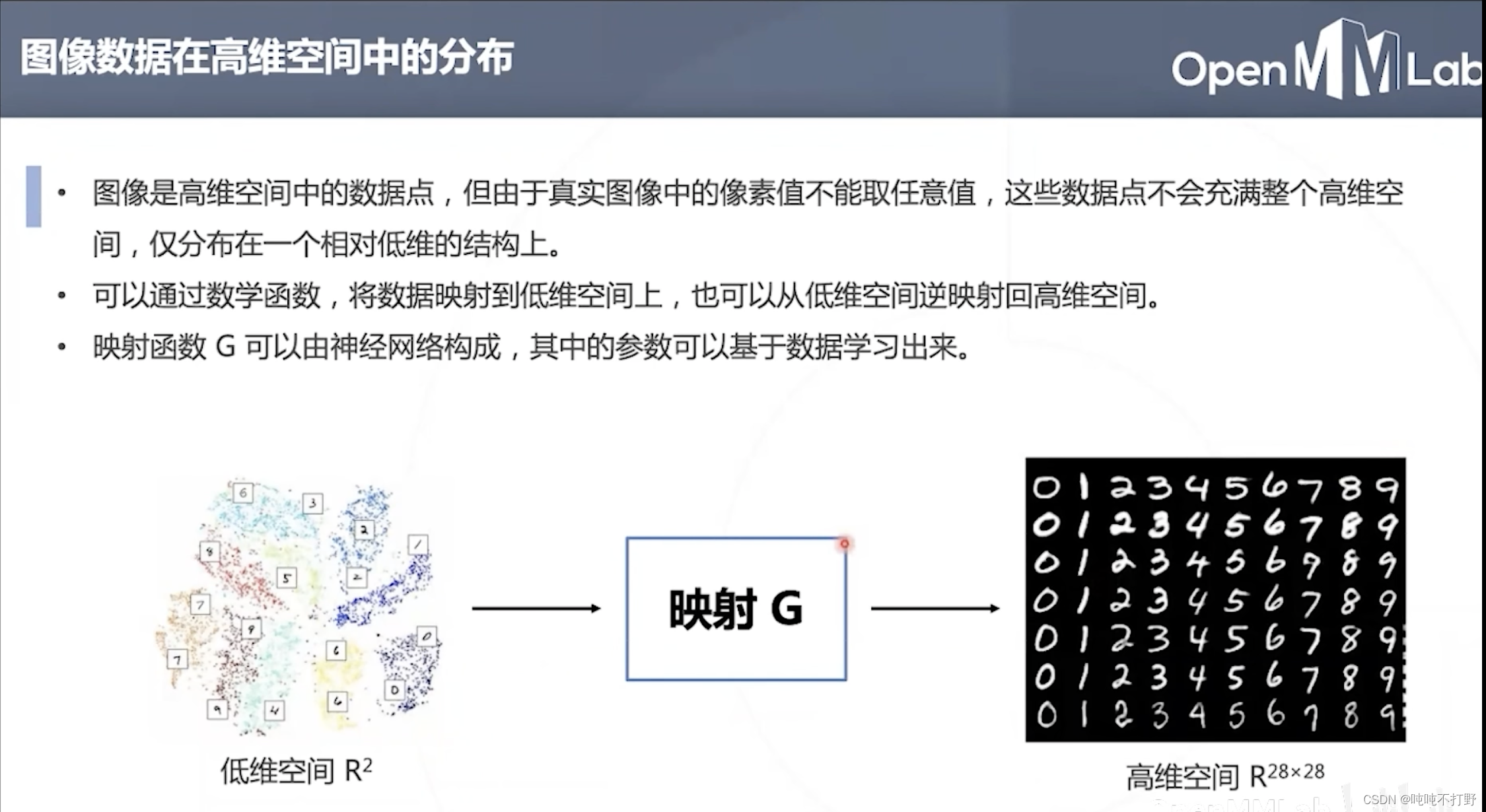
映射G就是对抗生成网络里的生成器,

如何用神经网络表示数据分布?
- 先假设数据分布是高斯或者均匀分布,以这个分布去生成随机向量
- 用生成网络 G G G对上一步生成的随机变量进行变换,产生一个复杂的概率分布 p x p_x px
- 调整 G G G网络的参数,使得 p x p_x px拟合 p d a t a p_{data} pdata
- 直到 p z p_z pz+ G G G可以隐式表示 p d a t a p_{data} pdata,即:从 p z p_z pz采样,再经过 G G G网络变换( p x p_x px概率分布调整),等效于从 p d a t a p_{data} pdata采样。
- 也就是输入网络的随机向量基于的简单分布 p z p_z pz,和网络 G G G生成的概率分布 p x p_x px,来共同拟合 p d a t a p_{data} pdata,用两个串联的分布来拟合一个分布。
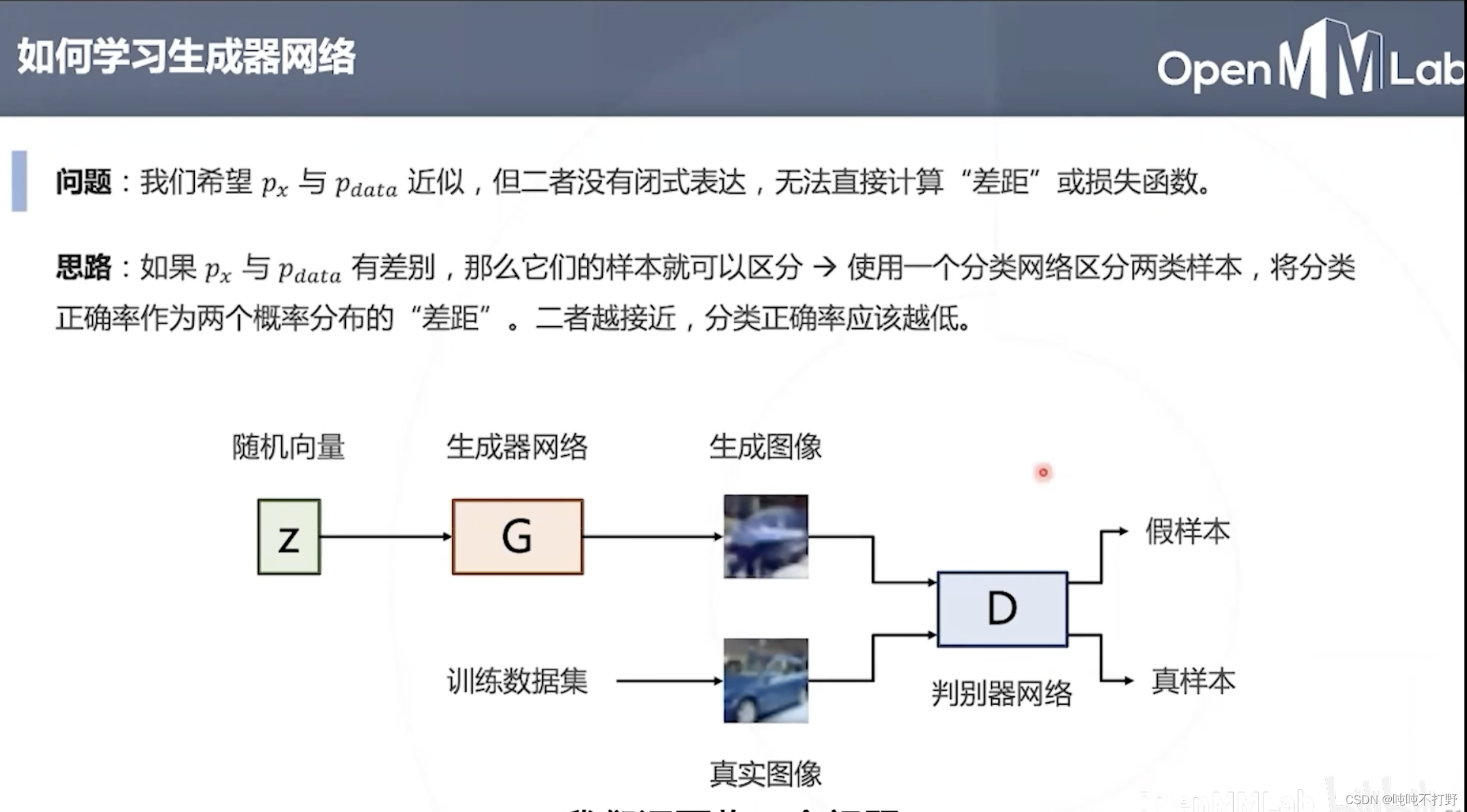
由于
p
x
p_x
px这个分布是神经网络表示的,
p
d
a
t
a
p_{data}
pdata是一个未知分布(与现有已知的分布都不符合的,通常不可解析表示)。
- 所以无法直接计算这两个分布的差距,或者损失函数(比如:KL散度,详见百度百科-相对熵)
- 因此,如果无法直接衡量这两个分布的差异,可以去衡量从他们分布中采样出的样本的差异。(比如:衡量均匀分布和正态分布的差距,可以去比较他们每次生成的随机数的差异)
- 可以使用一个分类网络(判别器网络),将分类正确率作为两个概率分布的差距
- 如果生成器生成的图像和真实图像会被这个分类网络分成一类(分类正确率越低),说明训练效果越好。即: p x p_x px和 p d a t a p_{data} pdata这两个分布越接近
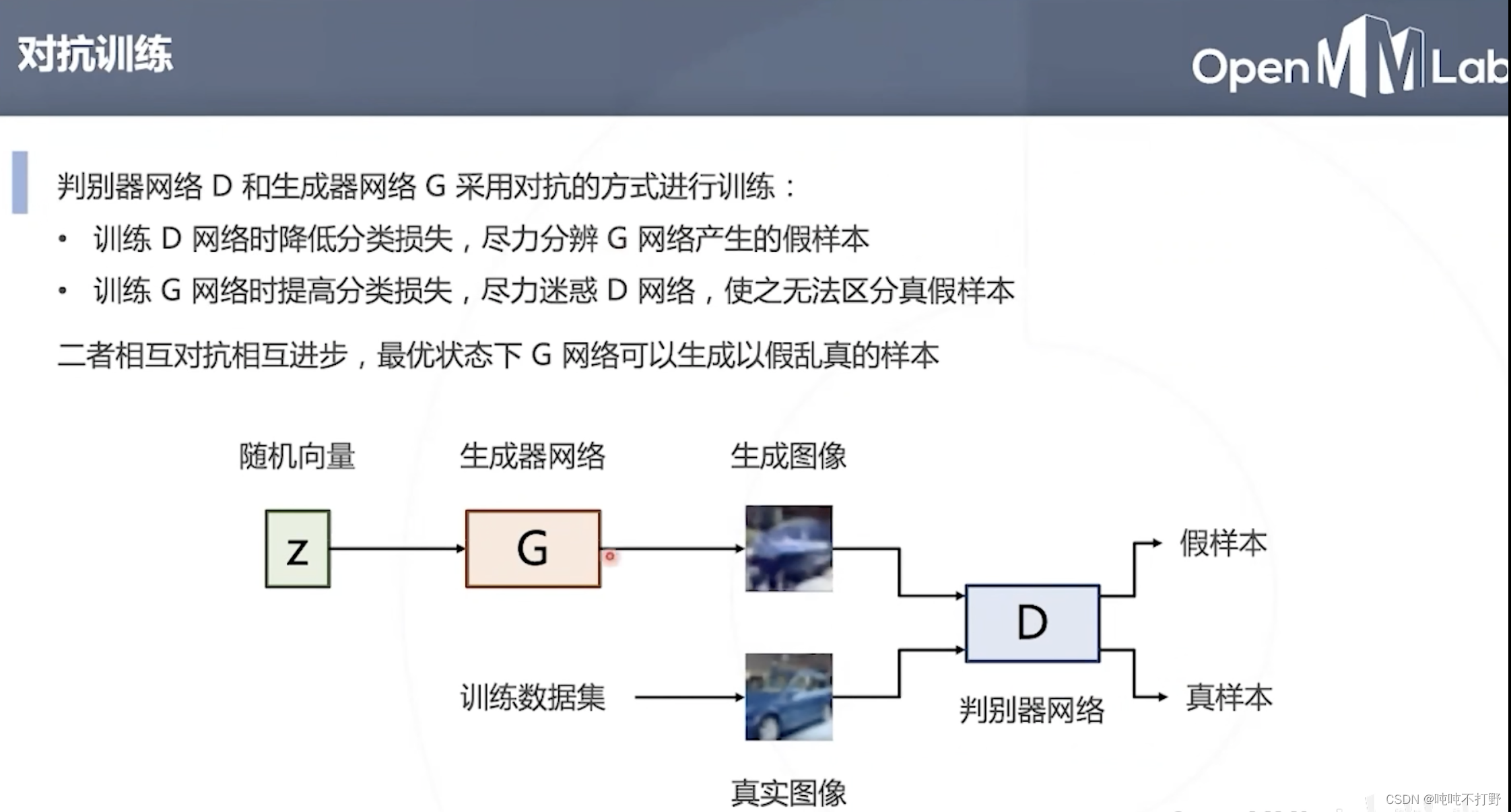
训练生成器网络G和判别器网络D时采取对抗的方式进行训练:
- 训练判别器网络D时,尽力降低分类损失,尽力分辨生成器网络G生成的假样本
- 训练生成器网络时,尽量提高分类损失(迷惑判别器网络D,使其把生成的样本和真实样本归为1类,使得生成的样本越来越接近真实样本-以假乱真)

- 对于给定的生成器网络(G),训练出最佳判别器网络,记录对应的分类损失(的负值),

![C国演义 [第三章]](https://img-blog.csdnimg.cn/48fe918b9d0c4f47a9e5a56a7a3aa117.png)