第三章
- 组合
- 分析
- 步骤
- 递归函数的返回值和参数
- 递归结束的条件
- 单层逻辑
- 组合总和 III
组合
力扣链接
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
- 提示:
1 <= n <= 20
1 <= k <= n
分析
暴力解法当然是用 for循环 :
n = 4, k = 2时:
int n = 4;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
cout << i << " " << j << endl;
}
}
n = 100, k = 3时:
int n = 100;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
for (int u = j + 1; u <= n; n++) {
cout << i << " " << j << " " << u << endl;
}
}
}
如果 k = 50呢? 就要用50个for循环. 有一个问题; 我们如何控制 50 个for循环呢
为了解决这种情况: 我们采用 回溯
回溯也是一种暴力, 但是可以用递归次数来解决for循环的层数
🗨️它是如何解决for循环的层数呢?
- 递归里面套用for循环 — — 每一次递归套用一个for循环, 那么我们解决递归的层数来控制for循环的层数
过程是非常抽象的, 但是递归的过程可以用 二叉树来做一个形象的理解
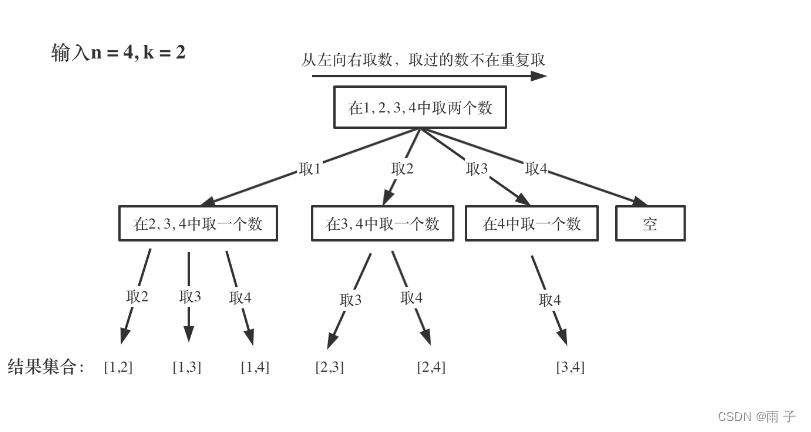
先看一个分支(纵向):
集合是 [1, 2, 3, 4], 从中任选一个 , 以取 1 为例子
然后集合是 [2, 3, 4], 从中任选一个就已经达到目标了, [1, 2], [1, 3], [1, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 2 为例子
然后集合是 [3, 4], 从中任选一个就已经达到目标了, [2, 3], [2, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 3为例子
然后集合是[ 4 ], 从中任选一个就已经达到目标了, [3, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 4为例子
然后集合是[ ], 就不能继续递归下去了
🗨️为啥集合是 [1, 2, 3, 4], 取 2, 然后剩余集合是 [3, 4]. 为啥不是[1. 3. 4 ]?
- 因为求的是
组合, 所以不用注意相同数值的顺序
如果剩余集合是 [1, 3, 4], 那么叶子结点就是 [2, 1], [2, 3], [2, 4]
这个时候, [1, 2] 和 [2, 1] 是重复的
⇒所以我们需要一个变量来控制下一层递归的开头
每次从集合中选取元素, 下一层递归的范围随着选取元素而缩减
步骤
递归函数的返回值和参数
一般回溯的返回值都是 void, 除非有特殊要求
需要定义两个全局变量, 一个来记录单层结果, 一个来记录全部结果
vector<int> path; // 记录单层结果
vector<int<vector<int>> result; // 记录全部结果
虽然这两个变量也可以放在参数列表里面, 但是这会导致参数列表过于冗杂, 而看不清回溯的逻辑
数组大小n 和 结果大小k 肯定是在参数列表中的
为了避免结果有重复的, 需要有一个变量来控制每一层递归的区间集合(开头), 我们一般用 startindex
⇒ 所以我们的递归函数应该如下:
vector<int> path;
vector<vector<int>> result;
void backtracking(int n, int k, int startindex )
递归结束的条件
path是用来记录单层结果的, 根据题目要求,
递归结束的条件是: path的大小是2
那么我们就把path收入result里面, 并不继续向下递归
if(path.size()) == k)
{
result.push_back(path);
return;
}
单层逻辑
单层逻辑肯定是一个for循环
for循环的起始点是 startindex, 终止点是 n
for(int i = startindex; i <= n; i++ )
{
}
我们先把沿途的数值收入path
for(int i = startindex; i <= n; i++ )
{
path.push_back(i);
}
继续向下递归, 此时的起始点就变成 i + 1
for(int i = startindex; i <= n; i++ )
{
path.push_back(i);
backtracking(n, k, i + 1);
}
回溯, 让一棵树的情况更加完整
for(int i = startindex; i <= n; i++ ) // 控制横向遍历
{
path.push_back(i); // 处理节点
backtracking(n, k, i + 1); // 纵向递归
path.pop_back(); // 回溯, 撤销处理的节点
}```
## 代码
```cpp
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n, int k, int startindex)
{
// 终止条件
if(path.size() == k)
{
result.push_back(path);
return ;
}
// 单层逻辑
for(int i = startindex; i <= n; i++)
{
path.push_back(i);
backtracking(n, k, i + 1);
path.pop_back(); // 回溯
}
}
vector<vector<int>> combine(int n, int k)
{
backtracking(n, k, 1);
return result;
}
};

组合总和 III
力扣链接
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
- 提示:
2 <= k <= 9
1 <= n <= 60
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n, int k, int startindex, int sum)
{
if(path.size() == k && sum == n)
{
result.push_back(path);
return ;
}
for(int i = startindex; i <= 9; i++)
{
path.push_back(i);
sum += i;
backtracking(n, k, i + 1, sum);
sum -= i;
path.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n)
{
backtracking(n, k, 1, 0);
return result;
}
};