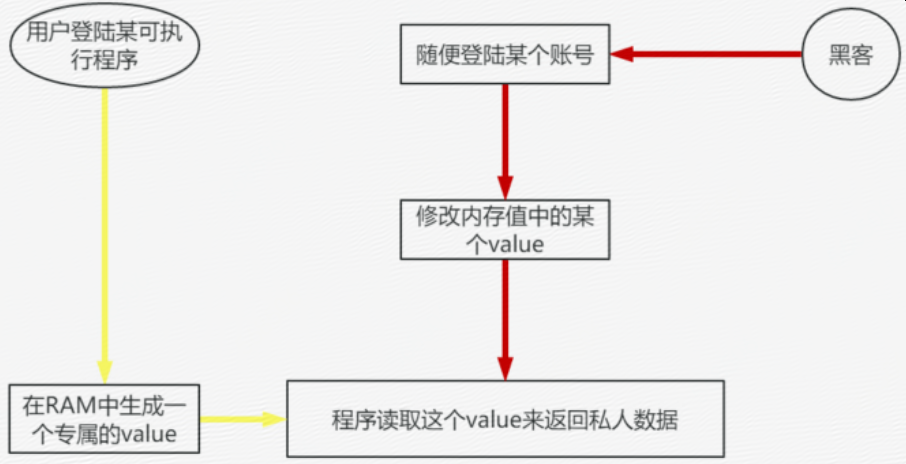
栈和队列基本概念
栈(Stack)和队列(Queue)都是常见的数据结构,用于存储和操作一组元素。它们在结构和操作方式上有所不同。
栈的基本概念:
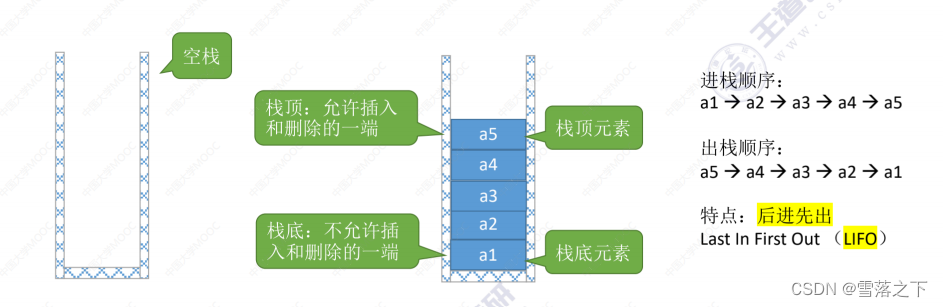
- 栈是一种线性数据结构,具有后进先出(LIFO)的特点。即最后入栈的元素最先被访问或移除。
- 栈有两个基本操作:压栈(push)和弹栈(pop)。压栈将元素添加到栈顶,而弹栈则将栈顶的元素移除并返回。
- 栈的插入和删除操作只能在栈顶进行,因此栈是一个只能从一端访问的数据结构。
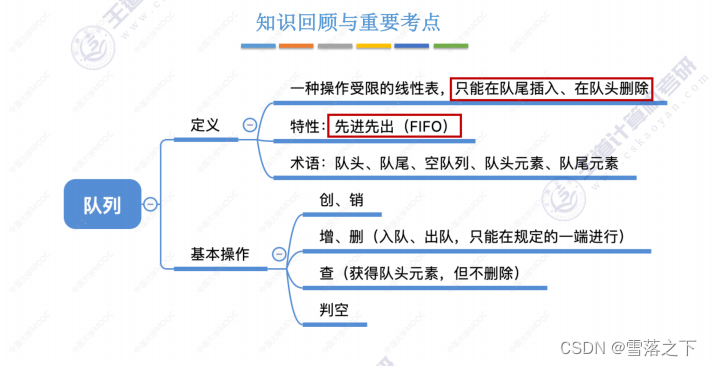
队列的基本概念:
- 队列是一种线性数据结构,具有先进先出(FIFO)的特点。即最早进入队列的元素最先被访问或移除。
- 队列有两个基本操作:入队(enqueue)和出队(dequeue)。入队将元素添加到队列的末尾,而出队则将队列的第一个元素移除并返回。
- 队列的插入操作在队列的末尾进行,而删除操作在队列的头部进行,因此队列是一个可以从两端访问的数据结构。
栈和队列的对比:
- 结构:栈和队列都是线性结构,但栈只有一个入口(栈顶)和一个出口(栈顶),而队列有一个入口(队尾)和一个出口(队头)。
- 插入和删除操作:栈的插入和删除操作只能在栈顶进行,而队列的插入操作在队尾进行,删除操作在队头进行。
- 访问顺序:栈按照后进先出的顺序访问元素,而队列按照先进先出的顺序访问元素。
- 应用场景:栈常用于函数调用、表达式求值、回溯算法等场景,而队列常用于任务调度、消息传递、缓冲区管理等场景。
总之,栈和队列都是重要的数据结构,在不同的应用场景中发挥着关键的作用。它们的不同特点和操作方式使得它们适用于不同的问题求解和算法设计。
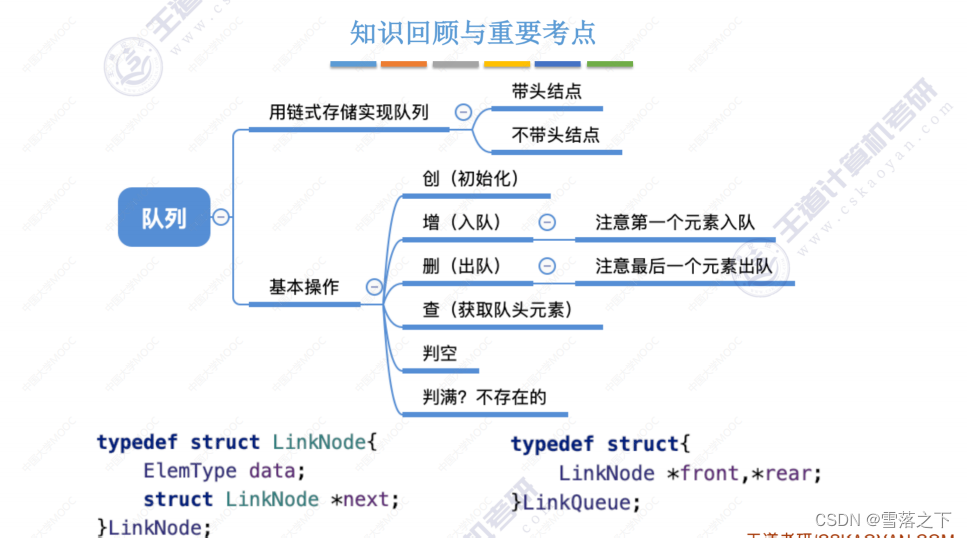
存储结构
栈和队列都是常见的数据结构,可以使用不同的存储结构进行实现,包括顺序存储结构和链式存储结构。下面是它们的定义、特点以及对比:
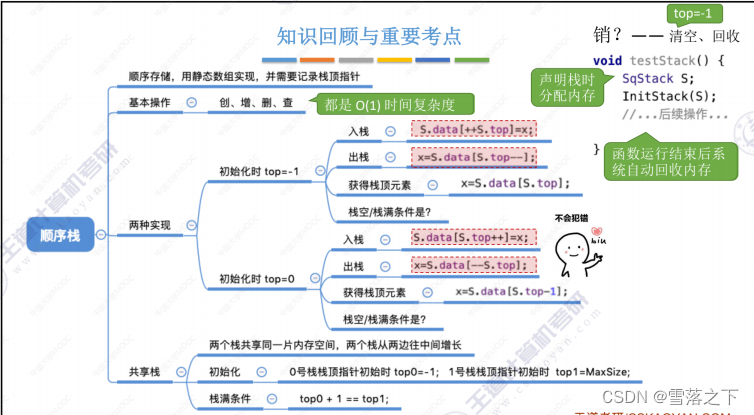
栈的顺序存储结构:
- 使用数组作为底层数据结构。
- 栈顶元素存储在数组的末尾,栈底元素存储在数组的开头。
- 使用一个指针来指示栈顶元素的位置。
- 插入和删除操作只发生在栈顶,时间复杂度为 O(1)。
栈的链式存储结构:
- 使用链表作为底层数据结构。
- 每个节点包含存储元素的数据域和指向下一个节点的指针域。
- 栈顶元素对应链表的头节点。
- 插入和删除操作通过修改链表的头节点来实现,时间复杂度为 O(1)。
队列的顺序存储结构:
- 使用数组作为底层数据结构。
- 队头元素存储在数组的开头,队尾元素存储在数组的末尾。
- 使用两个指针分别指示队头和队尾的位置。
- 插入操作在队尾进行,删除操作在队头进行,时间复杂度为 O(1)。
队列的链式存储结构:
- 使用链表作为底层数据结构。
- 每个节点包含存储元素的数据域和指向下一个节点的指针域。
- 队头对应链表的头节点,队尾对应链表的尾节点。
- 插入操作在链表尾部进行,删除操作在链表头部进行,时间复杂度为 O(1)。
顺序存储结构和链式存储结构的对比:
- 空间复杂度:顺序存储结构需要预先分配一定大小的连续内存空间,因此在空间利用上可能存在浪费。而链式存储结构则根据实际需要动态分配内存空间,更加灵活。
- 插入和删除操作:顺序存储结构的插入和删除操作通常需要移动元素,时间复杂度较高。链式存储结构通过改变指针的指向来实现插入和删除,时间复杂度为 O(1)。
- 扩展性:顺序存储结构的扩展性有限,当存储空间不足时需要进行重新分配。链式存储结构则可以根据需要动态添加节点,具有更好的扩展性。
- 内存效率:链式存储结构由于需要额外的指针域,相对于顺序存储结
构会占用更多的内存空间。
5. 访问效率:顺序存储结构的元素在内存中是连续存储的,对于 CPU 缓存等硬件有较好的利用效率,因此在访问速度上可能更快。而链式存储结构的元素在内存中是分散存储的,可能对 CPU 缓存不友好,访问速度稍慢。
选择顺序存储结构还是链式存储结构取决于具体的应用场景和需求。顺序存储结构适合于已知大小、频繁访问元素的场景。链式存储结构适合于频繁插入和删除操作、大小不确定的场景。
操作
以下是使用 C 语言实现栈和队列的基本操作的示例代码:
栈的操作
#include <stdio.h>
#define MAX_SIZE 100
typedef struct {
int data[MAX_SIZE];
int top;
} Stack;
void initStack(Stack *stack) {
stack->top = -1;
}
int isEmpty(Stack *stack) {
return stack->top == -1;
}
int isFull(Stack *stack) {
return stack->top == MAX_SIZE - 1;
}
void push(Stack *stack, int element) {
if (isFull(stack)) {
printf("Error: Stack is full\n");
return;
}
stack->top++;
stack->data[stack->top] = element;
}
int pop(Stack *stack) {
if (isEmpty(stack)) {
printf("Error: Stack is empty\n");
return -1;
}
int element = stack->data[stack->top];
stack->top--;
return element;
}
int peek(Stack *stack) {
if (isEmpty(stack)) {
printf("Error: Stack is empty\n");
return -1;
}
return stack->data[stack->top];
}
int main() {
Stack stack;
initStack(&stack);
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Peek: %d\n", peek(&stack)); // 输出:Peek: 30
printf("Pop: %d\n", pop(&stack)); // 输出:Pop: 30
printf("Pop: %d\n", pop(&stack)); // 输出:Pop: 20
printf("Is Empty: %d\n", isEmpty(&stack)); // 输出:Is Empty: 0
return 0;
}
队列的操作
#include <stdio.h>
#define MAX_SIZE 100
typedef struct {
int data[MAX_SIZE];
int front;
int rear;
} Queue;
void initQueue(Queue *queue) {
queue->front = -1;
queue->rear = -1;
}
int isEmpty(Queue *queue) {
return queue->front == -1;
}
int isFull(Queue *queue) {
return (queue->rear + 1) % MAX_SIZE == queue->front;
}
void enqueue(Queue *queue, int element) {
if (isFull(queue)) {
printf("Error: Queue is full\n");
return;
}
if (isEmpty(queue)) {
queue->front = 0;
}
queue->rear = (queue->rear + 1) % MAX_SIZE;
queue->data[queue->rear] = element;
}
int dequeue(Queue *queue) {
if (isEmpty(queue)) {
printf("Error: Queue is empty\n");
return -1;
}
int element = queue->data[queue->front];
if (queue->front == queue->rear) {
queue->front = -1;
queue->rear = -1;
} else {
queue->front = (queue->front + 1) % MAX_SIZE;
}
return element;
}
int front(Queue *queue) {
if (isEmpty(queue)) {
printf("Error: Queue is empty\n");
return -1;
}
return queue->data[queue->front];
}
int main() {
Queue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&
queue, 30);
printf("Front: %d\n", front(&queue)); // 输出:Front: 10
printf("Dequeue: %d\n", dequeue(&queue)); // 输出:Dequeue: 10
printf("Dequeue: %d\n", dequeue(&queue)); // 输出:Dequeue: 20
printf("Is Empty: %d\n", isEmpty(&queue)); // 输出:Is Empty: 0
return 0;
}
以上代码分别实现了栈和队列的基本操作,包括初始化、判断是否为空、判断是否为满、入栈/入队、出栈/出队、获取栈顶/队首元素等。在 main 函数中,通过调用这些函数对栈和队列进行操作,并输出结果。
逐行分析
以下是逐行分析提供的栈和队列操作的C语言代码:
#include <stdio.h>
#define MAX_SIZE 100
typedef struct {
int data[MAX_SIZE];
int top;
} Stack;
void initStack(Stack *stack) {
stack->top = -1;
}
代码的第一行包含了 <stdio.h> 头文件,用于输入输出操作。第二行定义了一个宏 MAX_SIZE,表示栈的最大大小。
接下来,定义了一个结构体 Stack,用于表示栈。该结构体包含一个整型数组 data,用于存储栈中的元素,以及一个整型变量 top,用于表示栈顶的索引。
initStack 函数用于初始化栈。它将栈顶 top 设置为 -1,表示栈为空。
int isEmpty(Stack *stack) {
return stack->top == -1;
}
int isFull(Stack *stack) {
return stack->top == MAX_SIZE - 1;
}
isEmpty 函数用于判断栈是否为空。它通过比较栈顶 top 的值是否等于 -1 来判断栈是否为空。如果相等,则返回 1,表示栈为空;否则返回 0。
isFull 函数用于判断栈是否已满。它通过比较栈顶 top 的值是否等于 MAX_SIZE - 1 来判断栈是否已满。如果相等,则返回 1,表示栈已满;否则返回 0。
void push(Stack *stack, int element) {
if (isFull(stack)) {
printf("Error: Stack is full\n");
return;
}
stack->top++;
stack->data[stack->top] = element;
}
int pop(Stack *stack) {
if (isEmpty(stack)) {
printf("Error: Stack is empty\n");
return -1;
}
int element = stack->data[stack->top];
stack->top--;
return element;
}
int peek(Stack *stack) {
if (isEmpty(stack)) {
printf("Error: Stack is empty\n");
return -1;
}
return stack->data[stack->top];
}
push 函数用于将元素压入栈中。它首先调用 isFull 函数判断栈是否已满。如果栈已满,则输出错误信息并返回;否则,将栈顶 top 加一,然后将元素存入数组 data 中的相应位置。
pop 函数用于弹出栈顶元素并返回。它首先调用 isEmpty 函数判断栈是否为空。如果栈为空,则输出错误信息并返回 -1;否则,将栈顶元素保存到变量 element 中,然后将栈顶 top 减一,最后返回 element。
peek 函数用于获取栈顶元素,但不弹出。它首先调用 isEmpty 函数判断栈是否为空。如果栈为空,则输出错误信息并返回 -1
;否则,直接返回栈顶元素。
int main() {
Stack stack;
initStack(&stack);
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Peek: %d\n", peek(&stack)); // 输出:Peek: 30
printf("Pop: %d\n", pop(&stack)); // 输出:Pop: 30
printf("Pop: %d\n", pop(&stack)); // 输出:Pop: 20
printf("Is Empty: %d\n", isEmpty(&stack)); // 输出:Is Empty: 0
return 0;
}
在 main 函数中,首先声明了一个 Stack 结构体变量 stack,然后调用 initStack 函数初始化栈。
接下来,通过调用 push 函数三次,将元素 10、20 和 30 压入栈中。
然后,使用 peek 函数获取栈顶元素并打印出来。预期输出为 “Peek: 30”。
接着,使用 pop 函数两次弹出栈顶元素并打印出来。预期输出为 “Pop: 30” 和 “Pop: 20”。
最后,使用 isEmpty 函数判断栈是否为空,并打印结果。预期输出为 “Is Empty: 0”,表示栈不为空。
整个程序执行完毕后,返回 0,表示正常退出。
多维数组的存储
多维数组是指包含多个维度的数组,例如二维数组、三维数组等。多维数组的存储可以通过两种常见的方式实现:行主序(Row-major order)和列主序(Column-major order)。
-
行主序(Row-major order)存储:
- 在行主序存储中,多维数组的元素按行进行存储。
- 对于二维数组,内存中的元素按行排列,即先存储第一行的所有元素,然后是第二行的所有元素,依此类推。
- 对于三维数组,元素的存储顺序是先按照第一维度的顺序存储,然后在每个一维数组内按行存储。
- 行主序存储的优势是可以提高缓存命中率,因为相邻元素在内存中的距离更近,更容易被缓存。
-
列主序(Column-major order)存储:
- 在列主序存储中,多维数组的元素按列进行存储。
- 对于二维数组,内存中的元素按列排列,即先存储第一列的所有元素,然后是第二列的所有元素,依此类推。
- 对于三维数组,元素的存储顺序是先按照第三维度的顺序存储,然后在每个一维数组内按列存储。
- 列主序存储在某些应用中可能更为常见,例如在某些科学计算中,对于矩阵运算等有较好的效率。
在实际编程中,多维数组的存储方式可以通过对下标的访问顺序来体现。在大多数编程语言中,多维数组都是按行主序存储的,例如 C、C++、Java 等。但也有一些编程语言支持列主序存储,例如 Fortran。
需要注意的是,多维数组的存储方式可能会影响程序的性能,特别是对于大型多维数组和对数组访问频繁的场景。选择合适的存储方式可以提高访问效率和性能。
特殊矩阵的压缩存储
特殊矩阵的压缩存储是一种优化矩阵存储方式,适用于稀疏矩阵(大部分元素为0)或具有特定规律的矩阵。
常见的特殊矩阵压缩存储方式有三种:行压缩存储、列压缩存储和十字链表存储。
-
行压缩存储(Compressed Row Storage,CRS):
- 该存储方式适用于稀疏矩阵。
- 矩阵的非零元素按行依次存储,同时记录每行中非零元素的列索引和值。
- 使用三个数组来存储矩阵的非零元素,以及每行的起始位置和结束位置。
- 优点是节省了存储空间,但访问元素的时间复杂度较高。
-
列压缩存储(Compressed Column Storage,CCS):
- 该存储方式同样适用于稀疏矩阵。
- 矩阵的非零元素按列依次存储,同时记录每列中非零元素的行索引和值。
- 使用三个数组来存储矩阵的非零元素,以及每列的起始位置和结束位置。
- 优点是节省了存储空间,同时访问元素的时间复杂度较低,但插入和删除操作较复杂。
-
十字链表存储:
- 该存储方式适用于具有特定规律的矩阵,如对称矩阵或带状矩阵。
- 使用两个链表来存储非零元素,分别按行和列连接,同时记录每个非零元素的行索引、列索引和值。
- 优点是适用于特定规律的矩阵,存储和访问效率较高,但实现相对复杂。
特殊矩阵的压缩存储可以大幅减少存储空间的占用,提高存储效率,并在某些情况下加速矩阵的运算和操作。选择适当的压缩存储方式取决于矩阵的特点和需要进行的操作。
栈,队列和数组的应用
栈、队列和数组是常用的数据结构,它们在计算机科学和软件开发中有广泛的应用。下面是它们的一些应用示例:
-
栈的应用:
- 表达式求值:栈可用于实现算术表达式的求值,如中缀表达式转换为后缀表达式并计算结果。
- 函数调用:函数调用时使用栈来存储局部变量、参数、返回地址等信息。
- 括号匹配:栈可以用于检查表达式中的括号是否匹配。
- 浏览器的前进后退:浏览器的前进后退功能可以使用栈来实现。
- 撤销操作:在文本编辑器、图形编辑器等应用中,撤销操作可以使用栈来管理历史操作记录。
-
队列的应用:
- 广度优先搜索:在图的遍历中,广度优先搜索算法可以使用队列来管理待访问的节点。
- 缓冲区管理:队列可以用于实现缓冲区,例如网络数据包传输中的数据缓冲队列。
- 多线程任务调度:多线程环境下,可以使用队列来实现任务调度,保证任务按顺序执行。
- 消息传递:在消息传递系统中,队列可用于在发送者和接收者之间传递消息。
-
数组的应用:
- 数据存储:数组是一种最基本的数据结构,用于存储和访问一组元素。
- 矩阵和图的表示:二维数组可以用于表示矩阵和图等数据结构。
- 排序算法:许多排序算法,如快速排序、归并排序等,都使用数组作为基本的数据结构。
- 搜索算法:在一维或二维数组中进行搜索,如二分查找、矩阵搜索等。
- 动态规划:动态规划算法中常常使用数组来存储中间计算结果。
这只是栈、队列和数组的一些常见应用示例,它们在实际应用中还有许多其他用途。栈、队列和数组的特点使它们在不同场景下具有优势,并为解决实际问题提供了方便和效率。