[细读经典]Megatron论文和代码详细分析(1)

前言

作为一款支持multi-node，multi-GPU的可以直接用来训练GPT3等世界上超大规模的自然语言模型的开源代码，Megatron值得被深入分析。

https://github.com/NVIDIA/Megatron-LMgithub.com/NVIDIA/Megatron-LM

我使用的版本是2020年9月12号最后commit的版本，在这里：

Xianchao-Wu/Megatron-LMgithub.com/Xianchao-Wu/Megatron-LM正在上传…重新上传取消

除了上面的代码部分，我主要参照的是：

一，论文：

https://arxiv.org/pdf/1909.08053.pdfarxiv.org/pdf/1909.08053.pdf

二，论文作者（Raul Puri）的演讲video（），在GTC2020（PPT时间是2020年3月6日）上面的讲解视频：

https://developer.nvidia.com/gtc/2020/video/s21496#developer.nvidia.com/gtc/2020/video/s21496#

三，论文作者（DR. MOHAMMAD SHOEYBI）另外一个video（登录姓名邮箱之后，可以免费观看），PPT上的时间是2019年10月17日：

Training Multi-Billion Parameter Language Models with Megatroninfo.nvidia.com/training-language-models-megatron-Reg-Page.html?ondemandrgt=yes正在上传…重新上传取消

第一部分：意义何在？

想玩转GPT3这样的超大规模模型（例如175billion parameters=1750亿），那就有必要详细了解一下multi-node（多机） multi-gpu（多卡）的工作原理和细节。

这里不过多探讨是否模型就如阿凡达胯下的鸟一样，越大越好，只是纯技术探讨。

通过对Megatron的学习，期望掌握的是：

Transformer如何通过multi-node, multi-GPU实现，例如其中的multi-head attention layer, point-wise feed-forward network；
如何实现三种并行：数据并行（mini-batch)，Tensor并行（把一个张量切成若干部分），和Pipeline并行（把一个网络的多个层进行按层切割），以及这三种并行的综合使用；
训练，重训，fine-tuning,多语言扩展等方面的具体的应用。

第二部分：论文的精细化解读

如果直接看论文，其实很多时候，即使多年从事NLP的researcher/engineer，估计也有一定的困难。因为从GPU并行的视角写的NLP的论文，本来就不多，这个论文还是侧重“模型并行”中的“张量Tensor并行”的实现方法。

第2.1节：先解释几个概念：

一，intra-layer model parallel approach和inter-layer model parallel approach的区别。猛一看，这两个的中文翻译都是“层内模型并行方法”。其实它们是有区别的：

即，inter-layer 并行，对应的是pipeline并行。例如上图右上方的6层网络，前三层给一个GPU，后三层给另外一个GPU。

而另外一个是intra-layer并行，对应的是tensor并行。例如上图右下方的6层网络，横向切一刀，即一个tensor张量，会被分配到不同的GPU上面。

二，orthogonal and complimentary 正交和互补

这个概念我看第一遍论文的时候，完全不理解。其实就是上面的两个图，竖向切了一刀vs.横向切了一刀，那么这两个切法，就是“正交的”（夹角90度）。而且这两个方法可以同时在一个代码中实现，具有“互补”的关系，即：

三，scaling efficiency的计算公式

76%这个数字在论文中出现了若干次，具体是怎么计算出来的呢？

前提条件：

条件一：512个GPU；通过Megatron的提案并行方法，达到的实际的整体算力是：15.1 PetaFLOPs per second（即，15.1*1000 TeraFLOPs）；

条件二：单个NVIDIA V100 32GB GPU，训练1.2 billion参数的模型的时候，算力为39 TeraFLOPs；

所以计算公式是： 15.1×100039×512=75.6% 。这个类似于衡量在多机多卡并行的时候，GPU的“利用率”的度量。

第2.2节：Model Parallel Transformers

直接看最核心的地方：

Model Parallel Transformers (模型并行Transformers，特别指的是Tensor Parallel，即Intra-layer）

Transformer中有两类比较重要的sublayers，一个是MLP（即双层线性层，张量的最后一个dimension从h到4h，然后再从4h回到h）；而另外一个是multi-head attention layer（多头注意力层）。

问题：怎么把这两种sublayers给切开到不同的GPU卡上？

第2.3节：MLP的多GPU实现

2.3.1 先看一个简单的问题，如何用多GPU来计算两个张量的乘积？（并行线性层）

假设公式为Y = XW，这里X是输入，W是权重，Y是输出；这是最简单的一个线性层。我们侧重看权重W被怎么切，因为这个是一个矩阵，其负责对张量X的最后一个维度进行“变形”。显然，我们可以：

横向切W，得到

或者，

纵向切W，得到W=[W1, W2]。

W的切分（二分为例）	示例	倒退X的切法
横向	[W1 W2]	[X1, X2]
纵向	[W1, W2]	X

这里有意思的地方在于，

当横向切分W，得到上下两个W1, W2子矩阵的时候，为了保证XW的运算结果，我们只能是对X进行纵向切割，并要求：

X1的最后一个维度=W1的最前一个维度；

X2的最后一个维度=W2的最前一个维度。

即：

这样的话，我们就可以把X1和W1放到一个GPU上；把X2和W2放到另外一个GPU上。它们都计算完毕之后，再相加（一个同步点），然后把相加的结果，回传给这两个GPU（如果有必要的话）。

上面是直观的示例，能不能拔高一些，来点更具有概括性的，有格调的？

当然可以，首先需要对X纵向切分，我们需要一个函数f来做这个事情，输入是X，而输出是X1, X2，且X=[X1, X2]。

这个函数，前向forward的时候，是对X进行切割split，（最后一个维度），例如(32, 100, 1024)被切割为两个(32, 100, 512)的形状的张量。那backward的时候呢？直观考虑，应该是切割的反操作，即拼接，我们就是要按照最后一列对“梯度”拼接了，类似于：

之后，我们还需要一个函数g，来对X1W1和X2W2相加。这个函数，前向forward是负责相加（每个gpu上的运算结果相加到一起，会涉及到gpu的wait，即一个gpu运行完毕之后，需要等待），这个可以通过pytorch的all-reduce函数实现；而backward的时候，鉴于X1W1和X2W2的形状相同，那么就是把相加之后的张量的梯度，原封不动的传递给每个gpu，继续反向传播的过程。即：

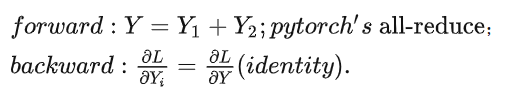
使用一个图形来表示这个所谓“row parallel linear layer”，我们就有：

而，当纵向切分W，得到左右W1, W2两个子矩阵的时候，鉴于W1, W2的第一个维度（行数）都没有变化，那么X的最后一个维度也不能边，从而有：

这样的话，同样的，我们可以把X和W1的乘积运算放一个GPU上；把X和W2的乘积运算放另外一个GPU上。

类似于前面的"row parallel lineary layer"，这里，纵刀流，我们称为“column parallel linear layer"，而其中我们也需要自定义两个函数，来实现多gpu并行下实现：

f函数，前向forward，因为每个gpu都是直接拿到X，所以forward就是identity function，相当于分发X到不同的gpu；

而backward的时候，每个gpu上的关于X的梯度，会相加得到新的关于X的梯度，即需要的是pytorch的all-reduce函数：总结即：

��:�(��);��:∂�∂�=∂�∂�|1+∂�∂�|2. ��ℎ′� all-reduce.

g函数，前向forward是需要实现对XW1和XW2的按照最后一个维度的拼接，即out=[XW1, XW2]；反向backward是一个简单的切割，类似于对 ∂�∂� 进行切分，得到每个gpu上都有一份： ∂�∂�� 。即：

��:�=[�1,�2];��ℎ′� all-gather;��:∂�∂��(��).

使用图形示例就是：

也就是说，我们有上面两种方法来实现一个最简单的“线性层”。

2.3.2 MLP的多GPU实现

先看MLP的部分：

在原始的Transformer中，MLP，即point-wise feed forward sublayer，是包括了两个线性层的，实现了hidden.size -> 4*hidden.size -> hidden.size的这样的变换的神经网络。

具体为：

XA -> RELU -> Dropout -> XB

（这里的A和B分别是线性层中的变换矩阵）

对应的超级简化后的代码为：

迷途小书僮：The Annotated Transformer的中文注释版（2）74 赞同 · 32 评论文章正在上传…重新上传取消

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."
    def __init__(self, d_model, d_ff, dropout=0.1):
        # d_model = 512
        # d_ff = 2048 = 512*4
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        # 构建第一个全连接层，(512, 2048)，其中有两种可训练参数：
        # weights矩阵，(512, 2048)，以及
        # biases偏移向量, (2048)
        self.w_2 = nn.Linear(d_ff, d_model)
        # 构建第二个全连接层, (2048, 512)，两种可训练参数：
        # weights矩阵，(2048, 512)，以及
        # biases偏移向量, (512)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        # x shape = (batch.size, sequence.len, 512)
        # 例如, (30, 10, 512)
        return self.w_2(self.dropout(F.relu(self.w_1(x))))
        # x (30, 10, 512) -> self.w_1 -> (30, 10, 2048)
        # -> relu -> (30, 10, 2048) 
        # -> dropout -> (30, 10, 2048)
        # -> self.w_2 -> (30, 10, 512)是输出的shape

上面的代码中，给定输入张量x，其shape为(batch.size, sequence.length, hidden.size)，然后首先经历self.w_1，之后是relu这个非线性函数，再走dropout，最后扔给的是第二个线性层，即self.w_2。

怎么安排XA和XB这两个线性层的并行性？是用“横刀流”，还是“纵刀流”？我们用笨方法思考，大不了四个组合形式了：横横，横纵，纵横，纵纵。

第一个线性层上：

按照对横刀流的思考，如果横向切割A，那么必须要纵向切割X，并且为了保证XA的完整性，需要X1A1+X2A2，即：

这就是说，横向切割权重A，必然需要一个同步点，如果这个同步点后面遇到的是线性函数，那当然可以把线性函数放这个同步点的前面，例如假设线性函数是y=ax，那么可以在X1A1和X2A2相加之前，先执行y=ax，并分别得到：aX1A1和aX2A2这两个分别的结果，然后它们再相加，也不影响最后的结果。

但是，relu或者bert中的gelu都是非线性函数，那么我们无法先执行这个非线性函数，然后再相加，即gelu(X1A1)+gelu(X2A2) != gelu(X1A1+X2A2）。即需要在gelu之前，设置一个同步点，从而让不同的gpu之间交互信息。

结论是什么？

如果第一个线性层，使用横刀流，则需要在gelu之前加一个”同步点“（gpu停下手中的计算任务，把数据交换了再说，如果有结束的早的gpu，那就wait到其他的gpu的结果计算出来为止。。。这会导致一定程度的gpu浪费）。

反过来看第一个线性层y=XA，如果使用纵刀流，结果会怎样呢？

鉴于XA1和XA2是通过最后一个维度拼接的，那么我们当然可以先计算gelu(XA1）和gelu(XA2)，然后把gelu(XA1)和gelu(XA2)拼接，这不影响最终的结果。这个就有意思了，可以看到为了计算gelu这个非线性函数，我们不需要设置一个同步点了！

所以，第一层线性层，我们优先选择纵刀流（纵向切割权重A）。

第二个线性层呢？

现在看看，当第一个线性层选了纵刀流的时候，结果就是传递给第二个线性层的X'是已经纵向切割的了，我们当然可以对B继续使用纵刀流，分别对XA1和XA2进行处理，这个时候就需要对B切三刀，得到四块了，有些琐碎。还有一个方法，就是对B使用横刀流，类似于：

这样，可以继续在gpu1上运行(XA1)*B1，以及在GPU2上运行(XA2)*B2。只有到最后计算完毕之后，才需要一个同步点，把两个gpu上分别的计算结果加在一起。

所以，第二层线性层，我们优先选择横刀流（横向切割权重B）。

总结起来，得到论文中的下图：

MLP的概要图，f和g是两个关键的函数，其中f来自“纵刀流”的f；而g来自“横刀流”的g

上图中：

一，X，表示输入张量，例如其shape为（batch.size, sequence.length, hidden.size)，例如取值为(32, 100, 1024)；

二，f，自定义的激活函数，forward就是identity 函数，即X传播到不同的GPU上面(copy-style)，而其backward则是类似于：

∂�∂�=∂�∂�|1+∂�∂�|2

这样的all_reduce函数（pytorch自己带的）；

这个函数，使用了前面讲述的"column parallel linear layer"的f函数！即：

只要纵刀流的f函数

三，XA1, XA2，即通过对A纵向一刀，得到的在两个gpu上运行的结果。当然，如果不是只切一刀，那当然可以使用更多的gpu来分别计算XA1, XA2, XA3, XA4...

四，GELU,非线性激活函数，Y1=GeLU(XA1)；Y2=GeLU(XA2)；

五，Y1B1和Y2B2，即通过对B横向一刀，得到的在两个gpu上运行的结果。当然可以切很多刀，把更小的块，扔给一个个gpu。

六：g，自定义的激活函数，前向forward的时候，是需要按照最后一个维度把Z1和Z2相加起来，即Z=Z1 + Z2，pytorch中的all_reduce函数可以实现这个“归约”操作；

而后向backward的时候，是类似identity的操作，即把一个完整的梯度张量，直接分发给各个gpu： ∂�∂��=∂�∂�(��) 。

这个函数，使用了前面讲述的"row parallel linear layer"的g函数！即：

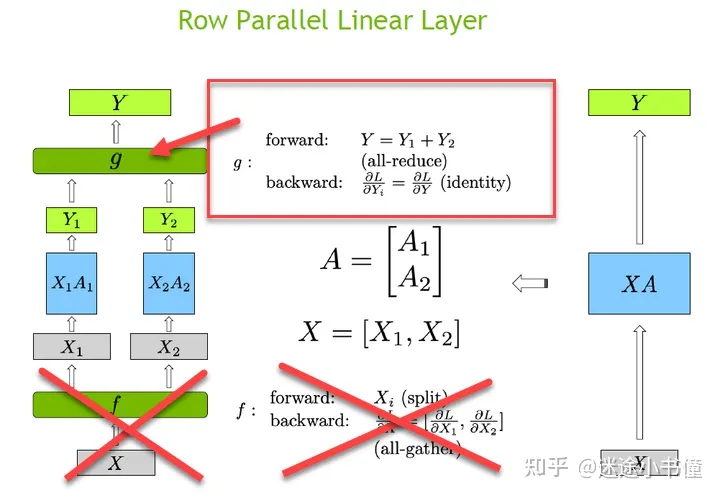
只要横刀流的g函数

把两个图放一起，更加直观一些：

两种线性层和最终MLP的应用的关系的示意图

2.3.3 MLP的pytorch代码实现

这样的话，我们看看MLP的代码实现。

显然，MLP先是使用了"column parallel linear layer"（纵刀流线性层），其次使用了"row parallel linear layer"（横刀流线性层）。

我们先看看column parallel linear layer的forward函数的代码实现：

（megatron/mpu/layers.py）

def forward(self, input_):
        # Set up backprop all-reduce. 输入的是整体h，输出的是4h/p被按照gpu分割之后的！
        input_parallel = copy_to_tensor_model_parallel_region(input_) 
        # 前向复制identity，后向全归约all-reduce（论文中的Figure 3.a中的f）
        # 原因：X在多个GPU上被简单复制（没有进行任何切割），类似X -> f -> [X, X, ..., X]
        # 这样的话，反向的时候，就是多个gpu上的X的整体，
        # 通过all_reduce合并到一起
        #（例如相加然后平均，或者直接element-wise相加 -> 这里是使用element-wise相加）
        # Matrix multiply.

        bias = self.bias if not self.skip_bias_add else None 
        # 当不“忽略bias”的时候，带上self.bias
        output_parallel = F.linear(input_parallel, self.weight, bias) 
        # import torch.nn.functional as F
        # X * A_i^T = (b, s, h) * (h, 4h/p) = (b, s, 4h/p) = output_parallel

        if self.gather_output: 
            # 作为独立的'column parallel linear layer'所需要的g函数，
            # 即forward使用all-gather：
            # All-gather across the partitions.
            output = gather_from_tensor_model_parallel_region(output_parallel) 
            # 前向拼凑，后向切割
            # 前向把各个GPU上的Y_i，进行拼凑，得到Y；
            # 即，从(b, s, 4h/p)拼凑到(b, s, 4h)的过程。
            # 后向的时候，把Y按照GPU的数量，进行切割，
            # 并送回到各个GPU。即，从(b, s, 4h)切割到(b, s, 4h/p)的过程。
        else:
            output = output_parallel 
            # 当前的'column parallel linear layer'
            # 作为GPU并行Transformer中的MLP的一部分的时候的用法：
            # TODO 注意，如果不gather，则实际在这里输出的是4h/p，
            # 是一个gpu上的结果！而不是整体的4h!
            # 这个部分非常重要，有助于理解selfattention中的每个tensor的维度！
        output_bias = self.bias if self.skip_bias_add else None
        return output, output_bias

或者使用下图示意：

下面继续看row parallel lineary layer的forward函数部分（横刀流的线性层）：

（megatron/mpu/layers.py）

    def forward(self, input_):
        # Set up backprop all-reduce. 输入的tensor是被分割到每个gpu的，
        # 输出的tensor是整体all-reduce之后的！
        if self.input_is_parallel: # Transformer's MLP使用这个部分:
            input_parallel = input_
        else: # 作为独立的row parallel线性层，使用这个部分：
            input_parallel = scatter_to_tensor_model_parallel_region(input_) 
            # 前向切割，后向拼凑
            # 如果有必要，先把输入inputs_=X按照?（应该是最后一列，即4h -> 4h/p）切割，
            # 按照gpu的数量。
            # 得到的是X_1, ..., X_p这样的，shape是?
            # (batch, seq, 4*hidden/p) 或者(seq, batch, 4*hidden/p)

        # Matrix multiply. [Y1*B1] to [Yi*Bi] in Figure 3(a):
        output_parallel = F.linear(input_parallel, self.weight) 
        # 注意，输入是X_i，而且经历的weight是A_i
        # 从4h/p -> h的linear (是对tensor的最后一列进行变换的！
        # 至于mini-batch方面，则是data-parallel的问题，这里不考虑！)
        # 相当于从X_i=(b, s, 4h/p) * A_i^T=(4h/p, h) -> (b, s, h)这样的结果。
        # 可以看到X按照最后一个维度被切割成了p份（gpu的数量); 
        # 然后经过线性层，从4h/p维度，被映射成了h维度。所以，最后的输出是(b, s, h).

        # All-reduce across all the partitions. [g function in Figure 3(a)]
        output_ = reduce_from_tensor_model_parallel_region(output_parallel) 
        # 前向全归约，后向复制(Figure 3(a) right-hand-side)
        # 对每个gpu上的(b, s, h)进行all_reduce，叠加（求平均），
        # 然后得到的是(b, s, h)，每个gpu上面都保持了最新的结果。

        if not self.skip_bias_add: # add:
            output = output_ + self.bias if self.bias is not None else output_ 
            # 把bias加到output_上
            output_bias = None
        else: # not add:
            output = output_
            output_bias = self.bias
        return output, output_bias

使用图示表示，即：

最后看看MLP(class ParallelMLP)中的forward函数：

（megatron/model/transformer.py）

    def forward(self, hidden_states):

        # [s, b, 4hp] (序列长度，批大小，4*一个划分上的隐层维度hp)? TODO-okay
        # 这里应该是一个整体的隐层维度大小（所有gpu的整体）[s, b, 4*h] 
        # -> NO, is [s, b, 4h/p] for one gpu!
        intermediate_parallel, bias_parallel = self.dense_h_to_4h(hidden_states)

        if self.bias_gelu_fusion:
             intermediate_parallel = \
                     bias_gelu_impl(intermediate_parallel, bias_parallel) # TODO
        else:
            intermediate_parallel = \
                self.activation_func(intermediate_parallel + bias_parallel)

        # [s, b, h] (序列长度，皮大小，隐层整体维度？！居然不是hp? TODO-okay) 
        # -> 应该不是hp; 应该是4hp -> h
        # RowParallelLinear : 负责对整体的hidden size，按照gpu进行切割处理
        output, output_bias = self.dense_4h_to_h(intermediate_parallel) 
        # is from [s, b, 4hp] to [s, b, h] (入分，出和)
        return output, output_bias

使用图示即：

（特别需要注意的是，首先使用的是“纵刀流”的f函数；其次使用的是“横刀流”的g函数）：

MLP的forward函数的代码截图

小结：

其一，在column parallel linear layer中，考虑了这个线性层独立使用，或者作为MLP的前半部分使用的情况；

其二，同样的，在row parallel linear layer中，考虑了这个线性层独立使用，或者作为MLP的后半部分使用的情况。

其三，ParallelMLP，就是把上面的两个线性层给“连起来”。图示为：

这里的f，来自column parallel linear layer；（纵刀流）

g，来自row parallel linear layer。（横刀流）。

2.3.4 Multi-head self-attention sublayer的实现

分析清楚了MLP的多gpu的实现之后，multi-head self-attention sublayer就相对简单一些了，因为其中的四个线性层，都可以复用已有的column/row parallel linear layers。

论文中的思想是每个head的计算，独立到一个gpu上面，类似于下面的示意：

上图的左边是通过f，先把X分发到多个GPU上（直接copy）。然后每个head相关的三个线性层转换Q, K, V，这三个都是用的“纵刀流linear layer”。在代码中，可以是使用一个h到3h的linear layer，最后再按照最后一个维度三等分，得到Q, K, V。

之后，计算 �1⊤�1 ，之后扔给softmax，再给dropout，之后就是V1和这个attention score进行乘积。得到Y1，再走一个“横刀流”的linear layer。

当然，实际在代码实现的时候，不一定是一个head占一个gpu，也可以是一个gpu上有若干head，然后每个head的hidden.size和gpu中head的数量，合在一起，进行linear layers和multi-head self-attention的计算。

下面是相对详细的代码部分：

def forward(self, hidden_states, attention_mask, layer_past=None,
                get_key_value=False):
        # hidden_states: [sq, b, h]

        # =====================
        # 1. Query, Key, and Value
        # =====================

        # Attention heads [sq, b, h] --> [sq, b, (np * 3 * hn)], 
        # np=每个gpu上head的数量, hn=每个head的隐层维度，np*3*hn=3h/p是一个gpu上的！
        # 不应该在这里的啊！这里的应该是3h作为输出的维度 TODO-okay（这里是“总调度”，
        # 不是各个gpu上的并行）
        # n/p * 3 * h/n = 3h/p finally 
        # (is actually for one gpu's hidden dimension!)
        # 纵刀流：三个linear layer都是纵刀流
        mixed_x_layer, _ = self.query_key_value(hidden_states) 
        # from h to 3h，这里还是整体的变换（非也，是h -> 3h/p）

        # ...

        # [sq, b, np, 3 * hn] --> 3 [sq, b, np, hn]， 
        # 每个gpu上的head的个数，之后是每个head对应的隐层的维度
        # 也就是说，head的数量，应该>= GPU的数量！
        (query_layer,
         key_layer,
         value_layer) = mpu.split_tensor_along_last_dim(mixed_x_layer, 3) 
        # 按照最后一列维度，三等分


        # ...

        # ===================================
        # 2. Raw attention scores. [b, np, s, s] 完成的是Q*K^T的运算！
        # ===================================
        
        # [b, np, sq, sk]
        output_size = (query_layer.size(1), 
                       query_layer.size(2), 
                       query_layer.size(0), # sq = sequench length of q
                       key_layer.size(0)) # sk = sequence length of k
        
        # [sq, b, np, hn] -> [sq, b * np, hn] 
        # batch * num_head_per_gpu -> 相乘之后，类似于组成了新的batch!
        query_layer = query_layer.view(output_size[2],
                                       output_size[0] * output_size[1], -1) 
        # [sq, b*np, hn]

        key_layer = key_layer.view(output_size[3],
                                   output_size[0] * output_size[1], -1) 
        # [sk, b*np, hn]

        # preallocating result tensor: [b * np, sq, sk]
        matmul_result = torch.empty(
            output_size[0]*output_size[1], 
            output_size[2], 
            output_size[3],
            dtype=query_layer.dtype, 
            device=torch.cuda.current_device())

        # Raw attention scores. matmul_result's shape=[b*np, sq, sk]
        matmul_result = torch.baddbmm(matmul_result, 
            query_layer.transpose(0, 1),   # from [sq, b*np, hn] to [b*np, sq, hn]
            key_layer.transpose(0,1).transpose(1, 2),  
            # from [sk, b*np, hn] to [b*np, sk, hn] and to  [b*np, hn, sk]
            beta=0.0, alpha=(1.0/self.norm_factor))
        # 得到的结果是: [b*np, sq, hn] * [b*np, hn, sk] -> [b*np, sq, sk]

        # change view to [b, np, sq, sk]
        attention_scores = matmul_result.view(*output_size)

        # ...
        # ===========================
        # 3. Attention probs and dropout
        # ===========================

        # attention scores and attention mask [b, np, sq, sk]
        attention_probs = self.scale_mask_softmax(attention_scores,
                                                  attention_mask)

        # This is actually dropping out entire tokens to attend to, which might
        # seem a bit unusual, but is taken from the original Transformer paper.
        # TODO where? to confirm?
        with mpu.get_cuda_rng_tracker().fork():
            attention_probs = self.attention_dropout(attention_probs) 

        # =========================
        # 4. Context layer. [sq, b, hp]
        # =========================

        # value_layer -> context layer.
        # [sk, b, np, hn] --> [b, np, sq, hn]

        # context layer shape: [b, np, sq, hn]
        output_size = (value_layer.size(1), 
                       value_layer.size(2), 
                       query_layer.size(0), 
                       value_layer.size(3)) 

        # change view [sk, b * np, hn] 
        value_layer = value_layer.view(value_layer.size(0),
                                       output_size[0] * output_size[1], -1)
        
        # change view [b * np, sq, sk]
        attention_probs = attention_probs.view(output_size[0] * output_size[1],
                                               output_size[2], -1)
        
        # matmul: [b*np, sq, sk] * [b*np, sk, hn] -> [b * np, sq, hn]
        context_layer = torch.bmm(attention_probs, value_layer.transpose(0,1)) 


        # =================
        # 5. Output. [sq, b, h], sq=sequence length of q, b=batch size, 
        # h=hidden size
        # =================

        # 也就是说，这里扔给self.dense的时候的, 
        # context_layer是已经被切割之后的了！所以其最后一个维度是hp=h/p，而不是h!
        output, bias = self.dense(context_layer) 
        # h-> h 的线性映射，RowParallelLinear

        if get_key_value:
            output = [output, present]

        return output, bias

如果把上面的代码进一步简化，其实是如下五步：

一，mixed_x_layer, _ = self.query_key_value(hidden_states) # h->3h的纵刀流；然后按照最后一个维度切割成三份：

(query_layer, key_layer, value_layer)=mpu.split_tensor_along_last_dim(mixed_x_layer,3)

二，Query和Key的attention score的计算：

matmul_result = torch.baddbmm(matmul_result,

query_layer.transpose(0,1), # from [sq, b*np, hn] to [b*np, sq, hn]

key_layer.transpose(0,1).transpose(1,2), # from [sk, b*np, hn] to [b*np, sk, hn] and to [b*np, hn, sk]

beta=0.0, alpha=(1.0/self.norm_factor)) # 得到的结果是: [b*np, sq, hn] * [b*np, hn, sk] -> [b*np, sq, sk]

三，attention mask和dropout的计算：

attention_probs = self.scale_mask_softmax(attention_scores, attention_mask) # This is actually dropping out entire tokens to attend to,

with mpu.get_cuda_rng_tracker().fork():

attention_probs = self.attention_dropout(attention_probs)

四，attention score和value.tensor的乘积：

context_layer = torch.bmm(attention_probs, value_layer.transpose(0,1))

五，输出的时候，最后加一个row parallel linear layer：

output, bias = self.dense(context_layer)# h-> h 的线性映射，RowParallelLinear

2.3.4 一个Transformer Layer的代码实现

即class ParallelTransformerLayer里面的代码分析：

在__init__函数里面有如下若干object:

        self.input_layernorm = LayerNorm(
            args.hidden_size,
            eps=args.layernorm_epsilon)

        # self attention:
        self.attention = ParallelSelfAttention(attention_mask_func, init_method,
                                               output_layer_init_method,
                                               layer_number)

        self.post_attention_layernorm = LayerNorm(
            args.hidden_size,
            eps=args.layernorm_epsilon)

        # MLP, h->4h->h
        self.mlp = ParallelMLP(init_method,
                               output_layer_init_method)

下面看其forward函数（精简之后的）：

    def forward(self, hidden_states, attention_mask, layer_past=None,
                get_key_value=False):
        # hidden_states: [b, s, h]
        # Layer norm at the begining of the transformer layer.
        
        ### 其一，layernorm
        layernorm_output = self.input_layernorm(hidden_states) # 输入layernorm

        ### 其二， Self attention.
        attention_output, attention_bias = \
            self.attention(layernorm_output,
                           attention_mask,
                           layer_past=layer_past,
                           get_key_value=get_key_value)

        ### 其三，Residual connection.
        if self.apply_residual_connection_post_layernorm: 
            # layernorm之后是残差链接(bert的原来的做法)
            residual = layernorm_output # 用的是layernorm之后的结果作为x
        else:
            residual = hidden_states # 原来的输入x

        ### 其四，MLP.
        mlp_output, mlp_bias = self.mlp(layernorm_output)

        ### 其五，Second residual connection.
        if self.apply_residual_connection_post_layernorm:
            residual = layernorm_output
        else:
            residual = layernorm_input

        ### 其六，re-enable torch grad to enable fused optimization.
        with torch.enable_grad():
            output = bias_dropout_add_func(
                mlp_output,
                mlp_bias.expand_as(residual),
                residual,
                self.hidden_dropout)

        if get_key_value:
            output = [output, presents]

        return output

2.3.5 最终的Transformer的实现

我们再看ParallelTransformer的实现代码：

即class ParallelTransformer(MegatronModule):

"""Transformer class."""

中的代码实现：

这里会涉及到pipeline并行的思想，即对输入的batch，再进行细分，让不同的mini-batch分别顺次执行，得到进一步的gpu使用率的优化。

这通过如下的代码实现：

# Number of layers.
assert args.num_layers % mpu.get_pipeline_model_parallel_world_size() == 0, \
            'num_layers must be divisible by pipeline_model_parallel_size'
    self.num_layers = args.num_layers // mpu.get_pipeline_model_parallel_world_size()

然后就是构造若干个ParallelTransformerLayer：

        # Transformer layers.
        def build_layer(layer_number):
            return ParallelTransformerLayer(
                attention_mask_func, init_method,
                output_layer_init_method, layer_number)
        offset = mpu.get_pipeline_model_parallel_rank() * self.num_layers
        self.layers = torch.nn.ModuleList(
            [build_layer(i + 1 + offset) for i in range(self.num_layers)])

接着看比较有嚼头的，forward函数：

    def forward(self, hidden_states, attention_mask, layer_past=None,
                get_key_value=False):

        # Checks.
        if layer_past is not None:
            assert get_key_value, \
                'for not None values in layer_past, ' \
                'expected get_key_value to be set'
        if get_key_value:
            assert not self.checkpoint_activations, \
                'get_key_value does not work with ' \
                'activation checkpointing'

        if mpu.is_pipeline_first_stage():
            # Data format change to avoid explicit tranposes : [b s h] --> [s b h].
            # If the input flag for fp32 residual connection is set, 
            # convert for float.
            if self.fp32_residual_connection:
                hidden_states = hidden_states.transpose(0, 1).contiguous().float() 
            # possibly from fp16 to fp32
            # Otherwise, leave it as is.
            else:
                hidden_states = hidden_states.transpose(0, 1).contiguous()

        if self.checkpoint_activations: 
            # 另外一种模型并行的方法 (Chen, T., Xu, B., Zhang, C., and 
            # Guestrin, C. Training
            # deep nets with sublinear memory cost. CoRR,
            # abs/1604.06174, 2016. URL http://arxiv:org/abs/1604:06174.)
            hidden_states = self._checkpointed_forward(hidden_states,
                                                       attention_mask)
        else:
            if get_key_value:
                presents = []
            for index in range(self.num_layers):
                layer = self._get_layer(index) # return self.layers[layer_number]
                past = None
                if layer_past is not None:
                    past = layer_past[index]

                ### 调用ParallelTransformerLayer的forward函数：###
                hidden_states = layer(hidden_states,
                                      attention_mask,
                                      layer_past=past,
                                      get_key_value=get_key_value)
                if get_key_value:
                    hidden_states, present = hidden_states
                    presents.append(present)
        
        # Final layer norm.
        if mpu.is_pipeline_last_stage(): 
            # 即当前gpu的rank = world_size - 1! 
            # 也就是说当前的gpu是"gpu并行群组"的最后一个
            # defined in megatron/mpu/initialize.py
            # Reverting data format change [s b h] --> [b s h].
            hidden_states = hidden_states.transpose(0, 1).contiguous()
            output = self.final_layernorm(hidden_states)
        else:
            output = hidden_states
        if get_key_value:
            output = [output, presents]

        return output

可以看到，除了最核心的:

### 调用ParallelTransformerLayer的forward函数：###

之外，还有不少零碎，例如判定是否是Pipeline并行的打头的或者结尾的网络层之类的。这些操作，留待下次分解。

码字不易，老铁们一键三联~~~ 吐槽拍砖，俺也坦然接受~~

导航：

迷途小书僮：[细读经典]Megatron论文和代码详细分析(2)102 赞同 · 41 评论文章