认识感知机
感知机接收多个输入信号,输出一个信号
感知机的信号只有“流/不流”(1/0)两种取值
0对应“不传递信号”,1对应“传递信号”。
输入信号被送往神经元时,会被分别乘以固定的权重。神经元会计算传送过来的信号的综合,只有当这个综合超过了某个界限值时,才会输出1。这也叫“神经元被激活”。界限值也叫阈值
在感知机中,“输入”也作为神经元节点,标为“输入单元”。感知机仅有两层:分别是输入层和输出层。输入层里的“输入单元”只负责传输数据,不做计算。输出层里的“输出单元”则需要对前面一层的输入进行计算。
感知机模型
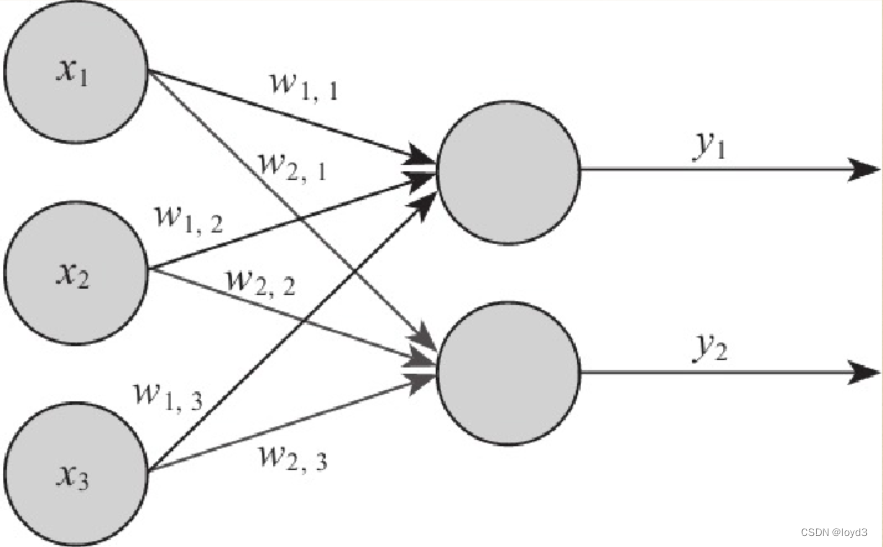
简单逻辑电路
与门(AND gate) :仅在两个输人均为1时输出1,其他时候则输出0。
与非门(NAND gate): 仅当书和同时为1时输出0其他时候则输出1。
或门:只要有一个输入信号是1,输出就为1
AND函数实现
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
b是偏置,w称为权重
偏置的值决定了神经元被激活的容易程度。
权重控制输入信号的重要性
与非门的实现
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
或门的实现
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
异或门XOR
异或门也被称为逻辑异或电路,仅当x1或x2中的一方为1时,才会输出1
用前面介绍的感知机是无法实现这个异或门的,因为异或门是非线性的而感知机只能表示由一条直线分割的空间
由曲线分制而成的空间非线性空间,由直线分割而成的空间称为线性空间。
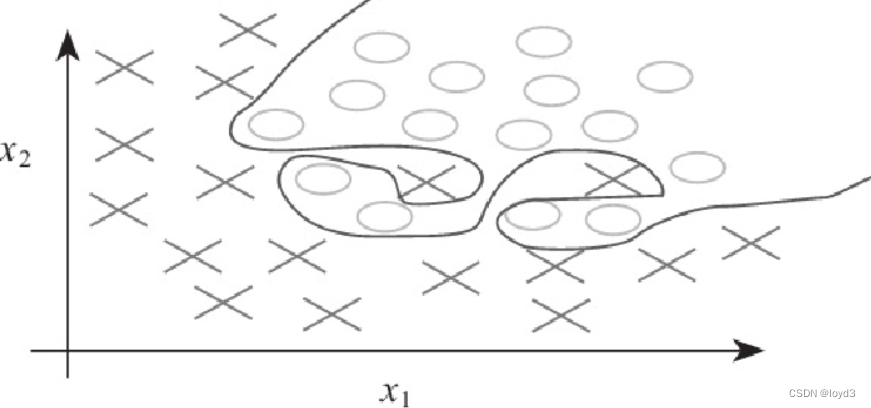
但是可以通过叠加层实现
实现如下:
def XOR(x1,x2):
s1= NAND(x1, x2)
s2= OR(x1, x2)
y= AND(x1, x2)
return y
异或门是一种多层结构的神经网络
将最左边的列称为第0层,中间的一列称为第1层,最右边的一列称为第2层。
叠加了多层的感知机也称为多层感知机
感知机通过叠加层能够进行非线性的标识,理论上还可以标识计算机进行的处理