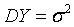---

• 压缩感知系列博客：
• 压缩感知入门①从零开始压缩感知
• 压缩感知入门②信号的稀疏表示和约束等距性
• 压缩感知入门③基于ADMM的全变分正则化的压缩感知重构算法

---

1. Problem

---

一个经典的压缩感知重构问题可以表示为

$$\underset{x}{\min }||x|{|}_{1}s.t.Ax=b+e\text{\hspace{1em}(1)}$$

其中，$A\in {\mathbb{R}}^{M\times N}$表示观测矩阵，$x\in {\mathbb{R}}^{N\times 1}$表示待求解信号，$b\in {\mathbb{R}}^{M\times 1}$表示测量向量，$e\in {\mathbb{R}}^{M\times 1}$表示测量噪声，其中$M<N$。这是一个典型的基于优化算法的压缩感知重构问题，它考虑了信号测量过程中引入的误差。

然而，在实际的使用过程中，通常观测矩阵本身也是存在误差的。在通信或雷达系统中，这种误差可能由时延、多普勒频移等引起，在测量系统中，可能由于观测矩阵的“失配”引起¹。该问题在数学上可以表示为

$$\underset{x}{\min }||x|{|}_{1}s.t.(A+E)x=b+e\text{\hspace{1em}(2)}$$

其中，$E\in {\mathbb{R}}^{M\times N}$表示观测矩阵受到的扰动。传统的压缩感知重构算法²对这一类扰动具有一定的鲁棒性³，但是针对观测矩阵扰动较大的情况，传统的算法可能会失效。因此，针对这种情况，需要设计一种同时考虑测量向量噪声和观测矩阵噪声的压缩感知重构算法。

不失一般性，可以先考虑$E$和$e$服从独立同高斯分布的情况，为了尽可能使得两种扰动最小，需要针对优化目标函数添加约束，即

$$\underset{x}{\min }\lambda ||x|{|}_1+||[Ee]|{|}_2^{2}s.t.(A+E)x=b+e\text{\hspace{1em}(3)}$$

这是一个总体最小二乘问题¹，可以等价为

$$\underset{x}{\min }\lambda ||x|{|}_1+\frac{||Ax-b|{|}_2^2}{||x|{|}_2^2+1}\text{\hspace{1em}(4)}$$

具体证明过程可参考⁴。其中$||x|{|}_1$是非光滑函数，而$\frac{||Ax-b|{|}_2^2}{||x|{|}_2^2+1}$是非凸函数，因此无法直接采用梯度下降法进行求解。

针对包含非光滑目标函数的优化问题，近端梯度下降法（Proximal Gradient Descent，PGD）提供了一个求解框架。其核心思想是，将目标函数拆解成光滑函数和不光滑函数两个部分，针对光滑部分可以直接求其梯度，针对不光滑部分则采用近端算子进行近似求解。其几何原理如图所示，第$k$次迭代时找一个近似函数去逼近原函数，求该近似函数的最优值，再去反推原函数的最优值。

不妨令

$$f(x)=\frac{||Ax-b|{|}_2^2}{||x|{|}_2^2+1}\text{\hspace{1em}(5)}$$

$$h(x)=\lambda ||x|{|}_1\text{\hspace{1em}(6)}$$

则原优化问题可重写为

$$\underset{x}{\min }f(x)+h(x)\text{\hspace{1em}(7)}$$

根据近端梯度法，有

$$z_k=x_k-{\mu }_k{g}_k\text{\hspace{1em}(8)}$$

x k + 1 = p r o x μ k h { z k } = a r g   m i n   { μ k h ( x ) + 1 2 ∣ ∣ z k − x ∣ ∣ 2 2 } (9) x_{k+1}=prox_{\mu_kh} \{z_k\}=arg\ min\ \{\mu_kh(x)+\frac 12||z_k-x||_2^2\}\tag{9} xk+1​=proxμk​h​{zk​}=arg min {μk​h(x)+21​∣∣zk​−x∣∣22​}(9)

该优化问题是典型的LASSO问题，利用软阈值函数能够实现快速求解。它的解为

p r o x μ k h { z k } = w t h r e s h ( x k − μ k g k , μ k λ ) (10) prox_{\mu_kh} \{z_k\}=wthresh(x_k-\mu_k g_k,\mu_k \lambda)\tag{10} proxμk​h​{zk​}=wthresh(xk​−μk​gk​,μk​λ)(10)

其中函数$f(x)$在$x_k$点的梯度为

$$g_k=\frac{2}{(||x_k|{|}_2^2+1{)}^2}[(||x_k|{|}_2^2+1)A^T(A{x}_k-b)-||A{x}_k-b|{|}_2^2{x}_k]\text{\hspace{1em}(11)}$$

在进行近端梯度迭代下降的过程中，迭代步长的选择将直接关系到算法收敛的速率。采用基于最速下降步长${\mu }_{s,k}$和最小化残差步长${\mu }_{m,k}$的自适应迭代步长，能够加快收敛速率

$${\mu }_k=\{\begin{array}{ll}{\mu }_{m,k}& \frac{{\mu }_{m,k}}{{\mu }_{s,k}}>\frac{1}{2}\\ {\mu }_{s,k}-\frac{{\mu }_{m,k}}{2}& \frac{{\mu }_{m,k}}{{\mu }_{s,k}}⩽\frac{1}{2}\end{array}\text{\hspace{1em}(12)}$$

其中，

$${\mu }_{s,k}=\frac{||x_k-x_{k-1}|{|}_2^2}{(x_k-x_{k-1}{)}^T(g_k-g_{k-1})}\text{\hspace{1em}(13)}$$

$${\mu }_{m,k}=\frac{(x_k-x_{k-1}{)}^T(g_k-g_{k-1})}{||g_k-g_{k-1}|{|}_2^2}\text{\hspace{1em}(14)}$$

采用了回溯线搜索来将步长的值限制在其稳定的下降区域中，每次迭代时检查线搜索条件

$$f(x_{k+1})<f(x_k)+(x_{k+1}-x_k{)}^T{g}_k+\frac{1}{2{\mu }_k}||x_{k+1}-x_k|{|}_2^2\text{\hspace{1em}(15)}$$

如果该条件不满足，则将${\mu }_k$收缩到原来的$\frac{1}{2}$并重复计算近端梯度直至满足该条件为止。理论上可以证明，选择的步长小于梯度$g_k$的利普西茨常数的倒数时，条件(15)都能够满足。

2. 仿真结果

---

测试输入采用随机生成的稀疏序列，序列长度100，稀疏度10，采样率50%。
观测矩阵采用随机高斯矩阵，对照算法采用经典的L1基追踪算法，对观测矩阵和测量向量分别添加-20 dB的高斯噪声，观察两种算法受到噪声的干扰程度。

从仿真结果可以看到，两种算法均能够恢复出原始信号的大致轮廓。但是基于Proximal Gradient Descent的算法具有更强的抗噪声性能，主要表现为其PSNR相比于L1算法高，且输出信号的平坦区域受到噪声干扰更小。

3. MATLAB算法

---

clear
close all
M=50;
N=100;
K=10;
%% Generate signal
% x=zeros(N,1);
% ind=randperm(N);
% x(ind(1:K))=randn(K,1);
% A=randn(M,N);% 
% A=A/max(abs(A(:)));% normalized
% x=x/max(abs(x(:)));% normalized
%% load default sensing matrix and signal
load input_dat.mat
snr_A=20;
snr_b=20;
sA=1/(10^(snr_A/10));
sb=1/(10^(snr_b/10));
%% Generate nosie matrix and noise array
E=sA*randn(size(A));
b=(A+E)*x+sb*randn(M,1);
%% signal reconstruction using L1 method and Proximal Gradient Descent method
x0=CS_linprog(A,b);
x1=PGD_TLS(A,b,N,0.01,0.1,10000);
%% error analysis
subplot(211)
plot(x,'*');hold on
plot(x0)
ylim([-1.2 1.2])
title(sprintf('PSNR of L1: %.2f dB',psnr(x0,x)));
subplot(212)
plot(x,'*');hold on
plot(x1)
ylim([-1.2 1.2])
title(sprintf('PSNR of PGD: %.2f dB',psnr(x1,x)));

function x=PGD_TLS(A,b,N,lam,mu0,ni)
AA=A'*A;
Ab=A'*b;
x0=zeros(N,1);
g=-2*Ab;
x=wthresh(-mu0*g,'s',mu0*lam);
y=1/(x'*x+1);
c=y*norm(A*x-b)^2;
for nn=1:ni
    g0=g;
    c0=c;
    g=2*y*(AA*x-Ab-c0*x);
    if (x-x0)'*(g-g0)==0
        mu=mu0;
    else
        mus=((x-x0)'*(x-x0))/((x-x0)'*(g-g0));
        mum=((x-x0)'*(g-g0))/((g-g0)'*(g-g0));
        if mum/mus>.5
            mu=mum;
        else
            mu=mus-mum/2;
        end
        if mu<=0
            mu=mu0;
        end
    end
    while 1
        z=wthresh(x-mu*g,'s',mu*lam);
        y=1/(z'*z+1);
        c=y*norm(A*z-b)^2;
        if c<=c0+(z-x)'*g+norm(z-x)^2/(2*mu)
            break
        end
        mu=mu/2;
    end
    mu0=mu;
    x0=x;
    x=z;
end

4. 源码地址

---

https://github.com/dwgan/Proximal-Gradient-method-for-Total-Least-Squares-problem

参考文献

---

1. Zhu, Hao, Geert Leus, and Georgios B. Giannakis. “Sparsity-cognizant total least-squares for perturbed compressive sampling.” IEEE Transactions on Signal Processing 59.5 (2011): 2002-2016. ↩︎ ↩︎

2. Chi, Yuejie, et al. “Sensitivity to basis mismatch in compressed sensing.” IEEE Transactions on Signal Processing 59.5 (2011): 2182-2195. ↩︎

3. Herman, Matthew A., and Thomas Strohmer. “General deviants: An analysis of perturbations in compressed sensing.” IEEE Journal of Selected topics in signal processing 4.2 (2010): 342-349. ↩︎

4. https://blog.csdn.net/qq_39942341/article/details/126436980 ↩︎