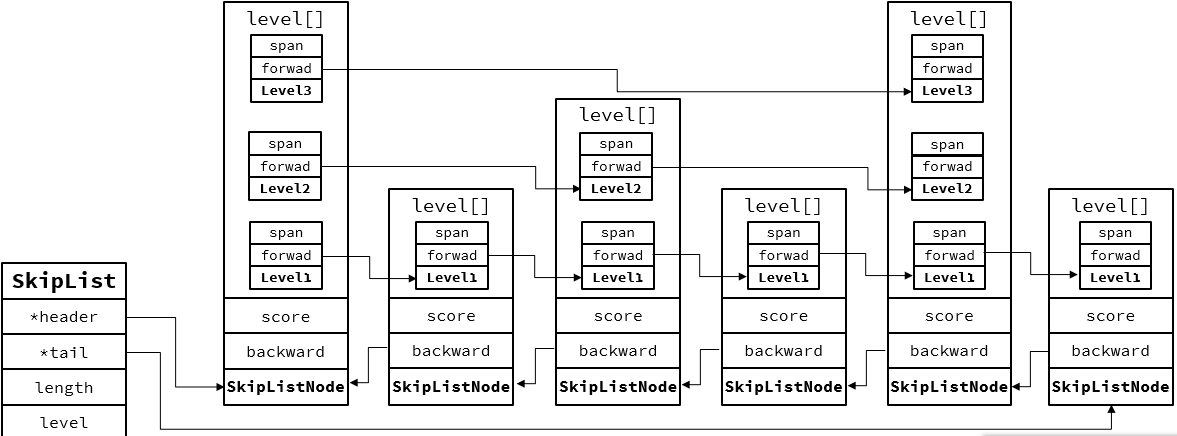
一元线性回归分析：

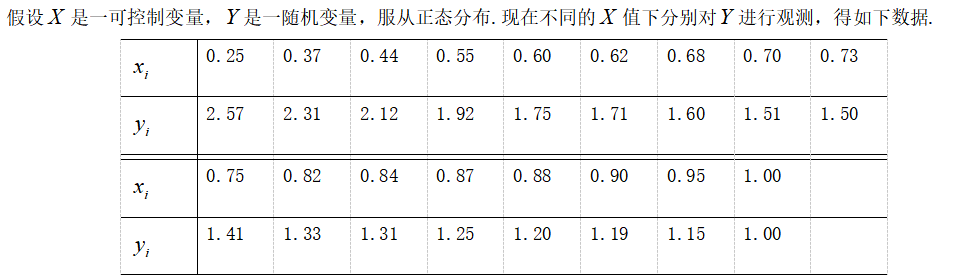
（1）假设X与Y有线性相关关系，求Y与X样本回归直线方程，并求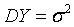
的无偏估计；
（2）检验Y和X之间的线性关系是否显著(α=0.05)；
（3）当X=x0时，求Y置信度为95%的预测区间；令：x0为学号后两位乘以0.01.
（4）为了把Y的观测值限制在（1.08，1.68），需把的值限制在什么范围(α=0.05)？

解答：
（1）首先，计算X和Y的样本均值和样本标准差：
$$\overline{x}=0.67,\overline{y}=1.77$$
$$s_x=0.23,s_y=0.49$$
然后，计算样本相关系数$r$：
$$r=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2{\sum }_{i=1}^n(y_i-\overline{y}{)}^2}}=-0.981$$
接下来，计算回归系数$b$和截距$a$：
$$b=r\frac{s_y}{s_x}=-2.13$$
$$a=\overline{y}-b\overline{x}=3.09$$
因此，Y与X的样本回归直线方程为$y=3.09-2.13x$。根据样本回归直线方程，可以计算出DY的无偏估计：
$${\hat{\sigma }}^2=\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{n-2}=0.026$$

（2）进行线性关系的显著性检验，需要计算回归平方和$SSR$、残差平方和$SSE$和总平方和$SST$：
$$SSR=\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2=5.07$$
$$SSE=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2=0.26$$
$$SST=\sum _{i=1}^n(y_i-\overline{y}{)}^2=5.33$$
根据F检验公式，计算F值：
$$F=\frac{SSR/1}{SSE/(n-2)}=100.13$$
查F分布表可知，在显著性水平为0.05时，自由度为(1, 7)时的临界值为4.30。因为计算得到的F值大于临界值，所以拒绝原假设，即认为Y和X之间的线性关系是显著的。

（3）当$x_0=0.56$时，代入样本回归直线方程可得：
$${\hat{y}}_0=3.09-2.13\times 0.56=1.87$$
根据样本回归直线方程和${\hat{\sigma }}^2$，可以计算出$x_0$处的预测区间：
$${\hat{y}}_0\pm t_{n-2,\alpha /2}\sqrt{{\hat{\sigma }}^2\left(1+\frac{1}{n}+\frac{(x_0-\overline{x}{)}^2}{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}\right)}$$
代入数据可得：
$$1.87\pm 2.306\times 0.231=(1.36,2.38)$$
因此，当X=0.56时，Y的置信度为95%的预测区间为(1.36, 2.38)。

（4）为了把Y的观测值限制在(1.08, 1.68)范围内，需要限制X的取值范围。根据样本回归直线方程，当$y=1.08$时，$x=0.98$；当$y=1.68$时，$x=0.28$。因此，限制X的取值范围为(0.28, 0.98)。进行检验，需要计算出限制后的回归平方和$SS{R}^{\prime }$、残差平方和$SS{E}^{\prime }$和总平方和$SS{T}^{\prime }$：
$$SS{R}^{\prime }=\sum _{i=1}^n({\hat{y}}_i^{\prime }-\overline{y}{)}^2=0.83$$
$$SS{E}^{\prime }=\sum _{i=1}^n(y_i-{\hat{y}}_i^{\prime }{)}^2=0.08$$
$$SS{T}^{\prime }=\sum _{i=1}^n(y_i-\overline{y}{)}^2=0.91$$
根据F检验公式，计算F值：
$$F=\frac{SS{R}^{\prime }/1}{SS{E}^{\prime }/(n-2)}=10.38$$
查F分布表可知，在显著性水平为0.05时，自由度为(1, 7)时的临界值为4.30。因为计算得到的F值大于临界值，所以拒绝原假设，即认为限制X的取值范围可以把Y的观测值限制在(1.08, 1.68)范围内。