【正项级数】敛散性判别

news2024/11/27 0:46:05

Hi！😊🥰大家好呀！欢迎阅读本篇文章正项级数敛散性判别。由于最近时间比较紧张，所以几乎没有使用公式编辑器，更多的内容多以图片形式呈现，希望本篇内容对你有帮助呀！
可能对你有帮助的：
【数项级数】无穷个数相加一定是个数吗？
【数项级数】敛散性判别

正项级数敛散性判别

相关定理
- - 例子
判别法
- - 前言
- 比较原则
- - 例题（利用比较原则）
- 比式判别法(达朗贝尔判别法)
- 根式判别法（柯西判别法）
- - 例题（使用比式/根式判别法）

之前我们宏观的了解到了数项级数，其定义，其判断其敛散性的方法，定理，推论等等……
当然这些定理准则对所有的数项级数都适用。
但我们希望在级数宏大的体系中，我们可以更加具体地研究某一类，各个击破。
最容易想到的一类就是求和的各项都是正的，即正项级数。求和的各项都是正的，其部分和只会单调增，我们只需要证明其有界即可。
即：
对于

\sum a_{n}(a_{n}≥0)，S_{n+1}=S_{n}+a_{n}≥S_{n}

S_{n}

}单调递增

判别法

前言

通过前面的定理，我们了解了正向级数的一些性质，以及如何判断正向级数时候收敛，即求部分和，若部分和构成的数列收敛到某一个值，则该正项级数收敛，且收敛值为部分和构成的数列的上确界。
但是，我们更希望，可以更加直接地根据a_{n}的性质，来直接判断一个级数是否收敛。
我们知道，当n→ $+\infty$ ，a_{n}→0,是级数收敛的必要条件。但是却不能根据a_{n}→0来判断一个级数是否收敛，所以我们希望可以有判别法来直接对a_{n}进行判断。
首先，举个例子， $a_{n}=\frac{1}{n}，\sum a_{n}发散，b_{n}=\frac{1}{n^2},\sum b_{n}收敛$ 。
当n趋于正无穷时， $a_{n} 和 b_{n}$ 都是无穷小量，那为什么一个收敛一个发散呢？
这是因为一个级数的敛散性不仅仅与n趋于正无穷时，数列必须是无穷小量有关，更与它趋于0的速度相关。正是因为， $a_{n} 和 b_{n}$ 趋于0的速度不一样快，结果导致一个收敛，一个发散。
由于我们知道 $\sum \frac{1}{n},\sum \frac{1}{n^2},\sum \frac{1}{n^α}$ …的敛散性，从而，我们可以将它们作为“标杆”，来判断一个级数的敛散性。

比较原则

在这里插入图片描述
在实际使用中，比较原则的极限更加方便。

例题（利用比较原则）

利用比较原则判断下列级数的敛散性。
(1)
在这里插入图片描述
（2）

（3）

（4）

（5）

（6）

（7）

（8）

（9）

根据比较原则，我们可以利用已知收敛或者发散级数作为比较对象来判别其他级数的敛散性。下面我们可以根据等比级数作为比较对象得到比式判别法和根式判别法

比式判别法(达朗贝尔判别法)

比式判别法是将等比级数作为比较对象得到的，在等比数列中，两项的商总是一个常数，所以称作公比。但是一般情况是，当n充分大时，两项之比不太可能总是一个数，但是在所有的数中，总会有一个上界，记作q，只要q小于1,那么就可称级数收敛。
比式判别法定义如下：
在这里插入图片描述
证明如下：

而对于一个级数是否收敛，对于有限项，我们是不太关心的，即使前有限项中，有的不满足前一项比后一项的比q＜1,我们可以改变，调整一下它，就好了。（因为改变有限项并不影响连三星期，只是收敛的会发生变化）我们关心当n充分大时的情况。
所以下面是比式判别法的极限形式。
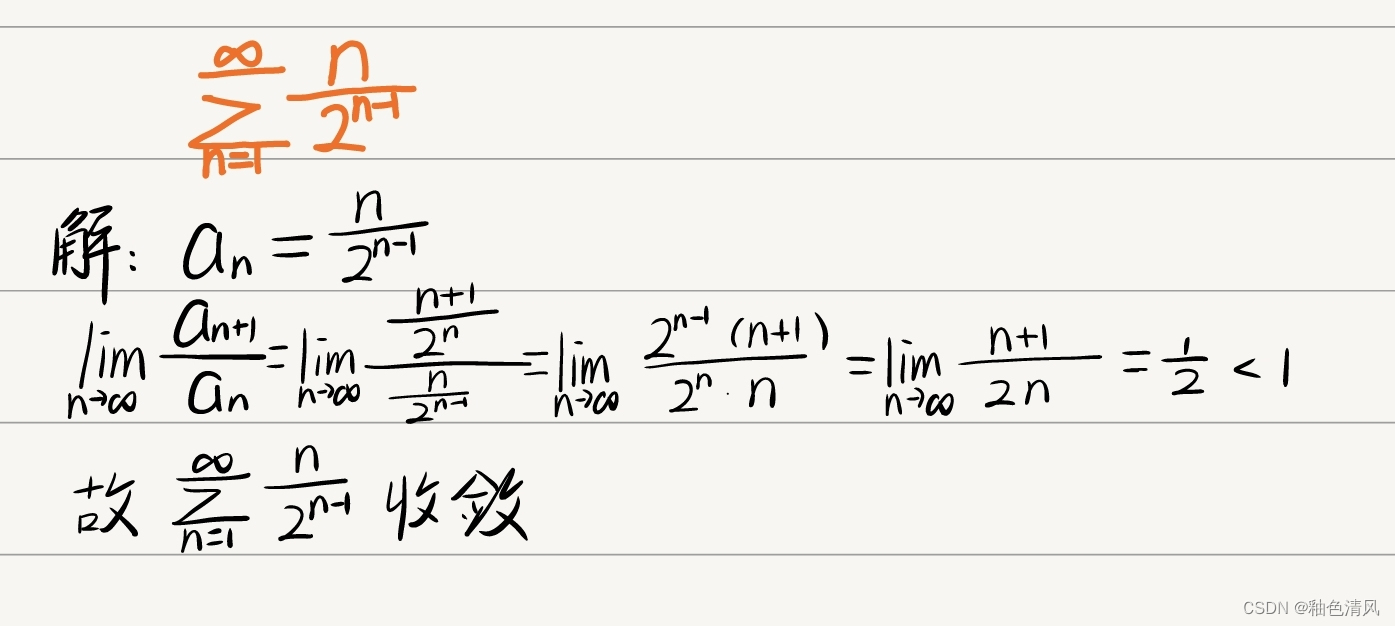
在这里插入图片描述