分类目录：《深入理解深度学习》总目录

相关文章：
·注意力机制（Attention Mechanism）：基础知识
·注意力机制（Attention Mechanism）：注意力汇聚与Nadaraya-Watson核回归
·注意力机制（Attention Mechanism）：注意力评分函数（Attention Scoring Function）
·注意力机制（Attention Mechanism）：Bahdanau注意力
·注意力机制（Attention Mechanism）：自注意力（Self-attention）
·注意力机制（Attention Mechanism）：多头注意力（Multi-head Attention）
· 注意力机制（Attention Mechanism）：带掩码的多头注意力（Masked Multi-head Attention）
·注意力机制（Attention Mechanism）：位置编码（Positional Encoding）
· Transformer：编码器（Encoder）部分

下图展示了Transformer模型中的编码器和解码器。我们可以看到，每个解码器中的多头注意力层都有两个输入：一个来自带掩码的多头注意力层，另一个是编码器输出的特征值。

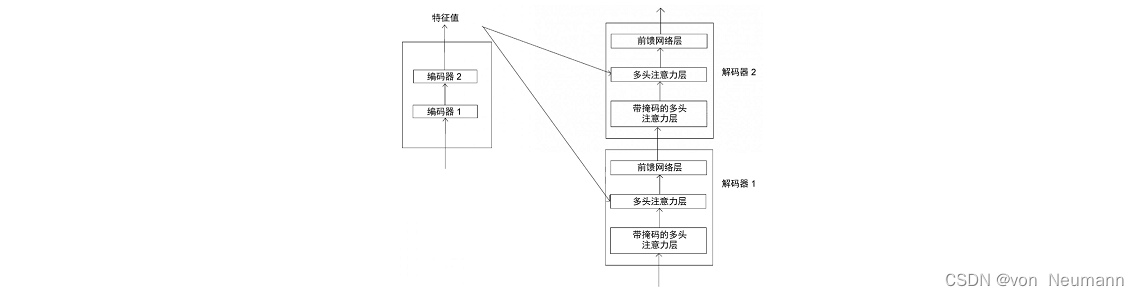
我们用$R$来表示编码器输出的特征值，用$M$来表示由带掩码的多头注意力层输出的注意力矩阵。由于涉及编码器与解码器的交互，因此这一层也被称为编码器—解码器注意力层。让我们详细了解该层究竟是如何工作的。多头注意力机制的第1步是创建查询矩阵、键矩阵和值矩阵。我们已知可以通过将输入矩阵乘以权重矩阵来创建查询矩阵、键矩阵和值矩阵。但在这一层，我们有两个输入矩阵：一个是$R$（编码器输出的特征值），另一个是$M$（前一个子层的注意力矩阵）。我们使用从上一个子层获得的注意力矩阵$M$创建查询矩阵$Q$，使用编码器输出的特征值$R$创建键矩阵和值矩阵。由于采用多头注意力机制，因此对于头$i$，需做如下处理：

• 查询矩阵$Q_i$通过将注意力矩阵$M$乘以权重矩阵$W_i^q$来创建。
• 键矩阵$K_i$和值矩阵$V_i$通过将编码器输出的特征值$R$分别与权重矩阵$W_i^k$、$W_i^r$相乘来创建，如下图所示。
  
  之所以用$M$计算查询矩阵，而用$R$计算键矩阵和值矩阵，是因为查询矩阵是从$M$求得的，所以本质上包含了目标句的特征。键矩阵和值矩阵则含有原句的特征，因为它们是用$R$计算的。为了进一步理解，让我们来逐步计算。第1步是计算查询矩阵与键矩阵的点积。查询矩阵和键矩阵如下图所示。需要注意的是，这里使用的数值是随机的，只是为了方便理解。
  
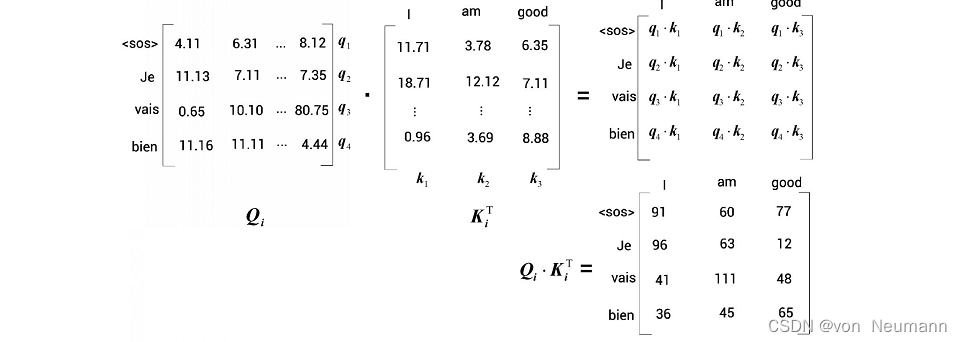
  通过观察上图中的矩阵$Q_i{K}_i^T$，我们可以得出以下几点。
• 从矩阵的第1行可以看出，其正在计算查询向量$q_1$（<sos>）与所有键向量$k_1$（I）、$k_2$（am）和$k_3$（good）的点积。因此，第1行表示目标词<sos>与原句中所有的词（I、am和good）的相似度。
• 同理，从矩阵的第2行可以看出，其正在计算查询向量$q_2$（Je）与所有键向量$k_1$（I）、$k_2$（am）和$k_3$（good）的点积。因此，第2行表示目标词Je与原句中所有的词（I、am和good）的相似度。
• 同样的道理也适用于其他所有行。通过计算$Q_i{K}_i^T$，可以得出查询矩阵（目标句特征）与键矩阵（原句特征）的相似度。

计算多头注意力矩阵的下一步是将$Q_i{K}_i^T$除以$\sqrt{d_k}$，然后应用Softmax函数，得到分数矩阵。接下来，我们将分数矩阵乘以值矩阵$V_i$，得到注意力矩阵$Z_i$，如下图所示。

目标句的注意力矩阵$Z_i=[z_1,z_2,z_3,z_4{]}^T$是通过分数加权的值向量之和计算的。为了进一步理解，让我们看看Je这个词的自注意力值$z_2$的计算方法：
$$z_2=0.98\times v_{\text{I}}+0.02\times v_{\text{am}}+0.00\times v_{\text{good}}$$

Je的自注意力值$z_2$是通过分数加权的值向量之和求得的。因此，$z_2$的值将包含98%的值向量$v_{\text{I}}$和2%的值向量$v_{\text{am}}$。这个结果可以帮助模型理解目标词Je指代的是原词I。同样，我们可以计算出$h$个注意力矩阵，将它们串联起来。然后，将结果乘以一个新的权重矩阵$W_0$，得出最终的注意力矩阵，如下所示：
$$\text{Muti-head Attention}=\text{Concatenate}(Z_1.Z_2,\cdots ,Z_h)W_0$$

将最终的注意力矩阵送入解码器的下一个子层，即前馈网络层。

参考文献：
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015
[2] Aston Zhang, Zack C. Lipton, Mu Li, Alex J. Smola. Dive Into Deep Learning[J]. arXiv preprint arXiv:2106.11342, 2021.
[3] 车万翔, 崔一鸣, 郭江. 自然语言处理：基于预训练模型的方法[M]. 电子工业出版社, 2021.
[4] 邵浩, 刘一烽. 预训练语言模型[M]. 电子工业出版社, 2021.
[5] 何晗. 自然语言处理入门[M]. 人民邮电出版社, 2019
[6] Sudharsan Ravichandiran. BERT基础教程：Transformer大模型实战[M]. 人民邮电出版社, 2023
[7] 吴茂贵, 王红星. 深入浅出Embedding：原理解析与应用实战[M]. 机械工业出版社, 2021.