前篇讨论了TD算法将MC同Bootstrap相结合,拥有很好的特性。本节所介绍的Eligibility Traces,其思想是多个TD(n)所计算预估累积收益按权重进行加权平均,从而得到更好的累积收益预估值。
价值预估模型的参数更新式子可以调整为:
1. Off-line λ-return
从式子中可以看出,必须要在一个episode结束后,才能计算各个时刻t下的值,因此同MC算法一样,模型在episode期间参数是不更新,所以该算法称之为off-line λ-return algorithm。
从式子上看,λ-return算法可以视为通过调整值到达TD(1)~TD(n)的中间状态。当
时,此时
,即为TD(1)。而当
时,此时
,即为MC算法。
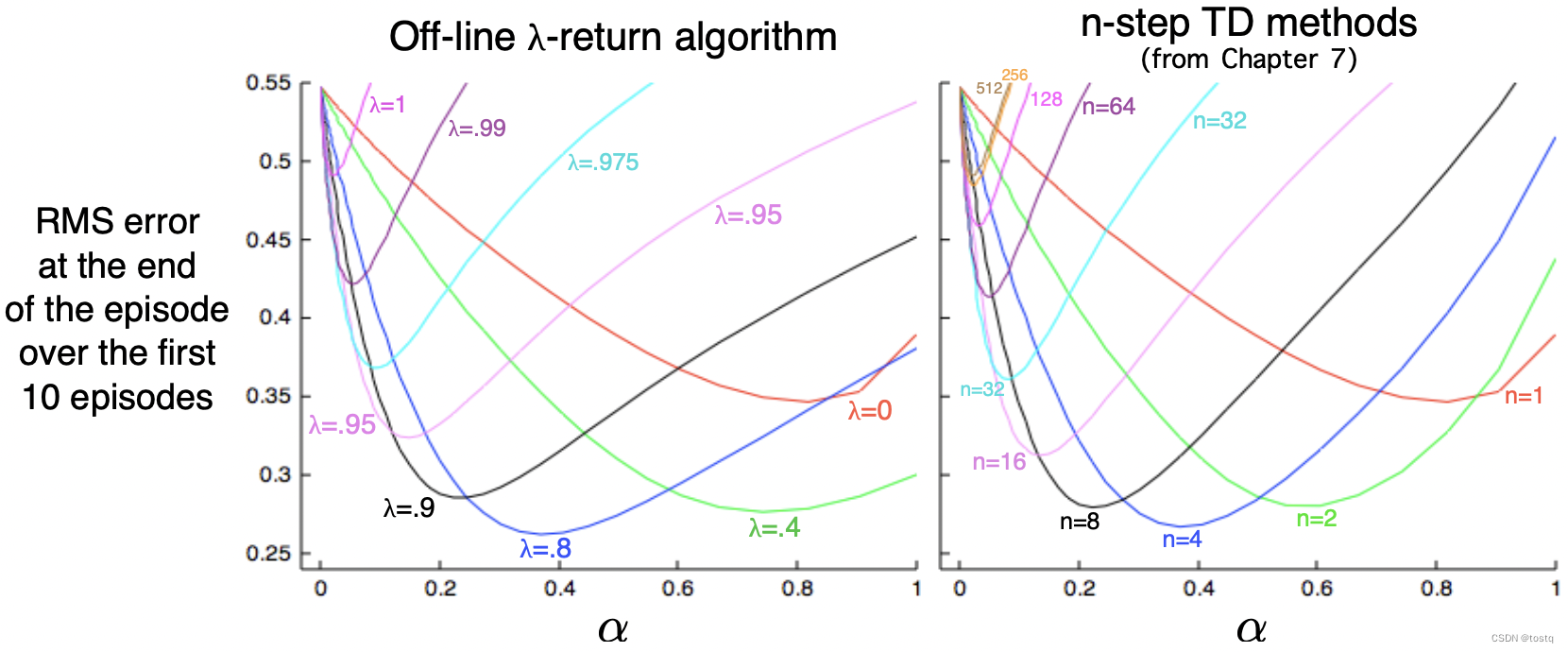
下图比较Off-line λ-return算法同TD算法效果,可以看出特别当值较高时,而n相对较少时,λ-return算法的效果要好于TD算法。
2. TD(λ)
TD(λ)相比于Off-line λ-return主要有三点升级:
-
TD(λ)可以在episode期间每个时刻t都更新,因此可以加速模型训练。
-
TD(λ)的计算被平均分配在episode期间每个时刻t,而不是在episode结束后统一计算
-
TD(λ)可以于连续场景下,Off-line λ-return的
计算必须要终态,否则是无法计算的
TD(λ)在每个episode开始时,会初始化eligibility trace向量
价值预估模型的参数更新式子可以调整为:
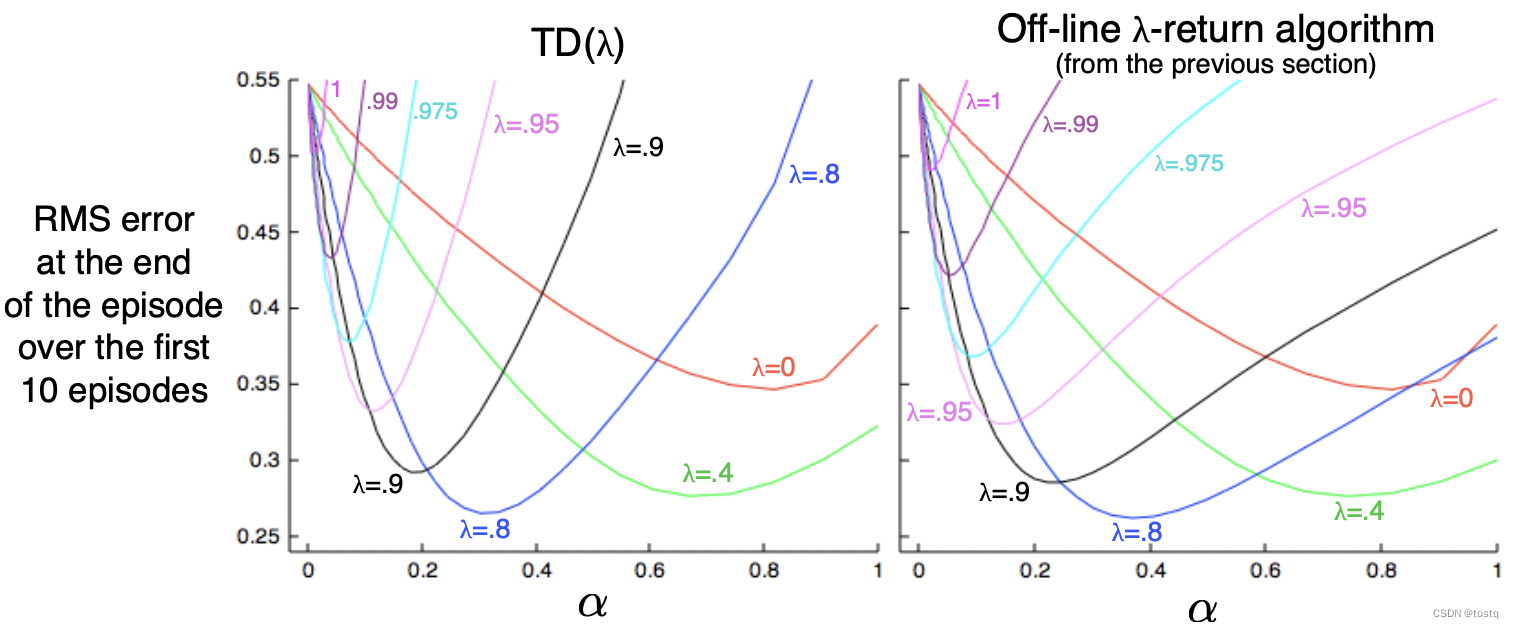
我们从式子上直观看,TD(λ)实际上是添加梯度更新的动量,其同Momentum优化器思想是相似的。下图比较了TD(λ)和Off-line λ-return算法,可以看出当较大时,TD(λ)效果是不如的,但当
较小时,两者的效果是接近的。
3. The Online λ-return Algorithm
对于某些连续场景(没有终态),很难直接通过Off-line λ-return进行计算,Truncated λ-return方法通过某个固定窗口h来截断,此时就不需要等待episode结束后才能更新。
基于这种思想,Online λ-return算法在episode期间时刻t都可以根据当前,通过Truncated λ-return来更新模型参数。假设当前位于某episode的时刻h,此时会进行如下更新过程:
可以看出仅在episode的时刻h就涉及了h次参数更新,Online λ-return算法相比于offline方法,其计算量是指数级提升,但是从下图的效果比较上看,Online λ-return方法是要优于offline方法的。
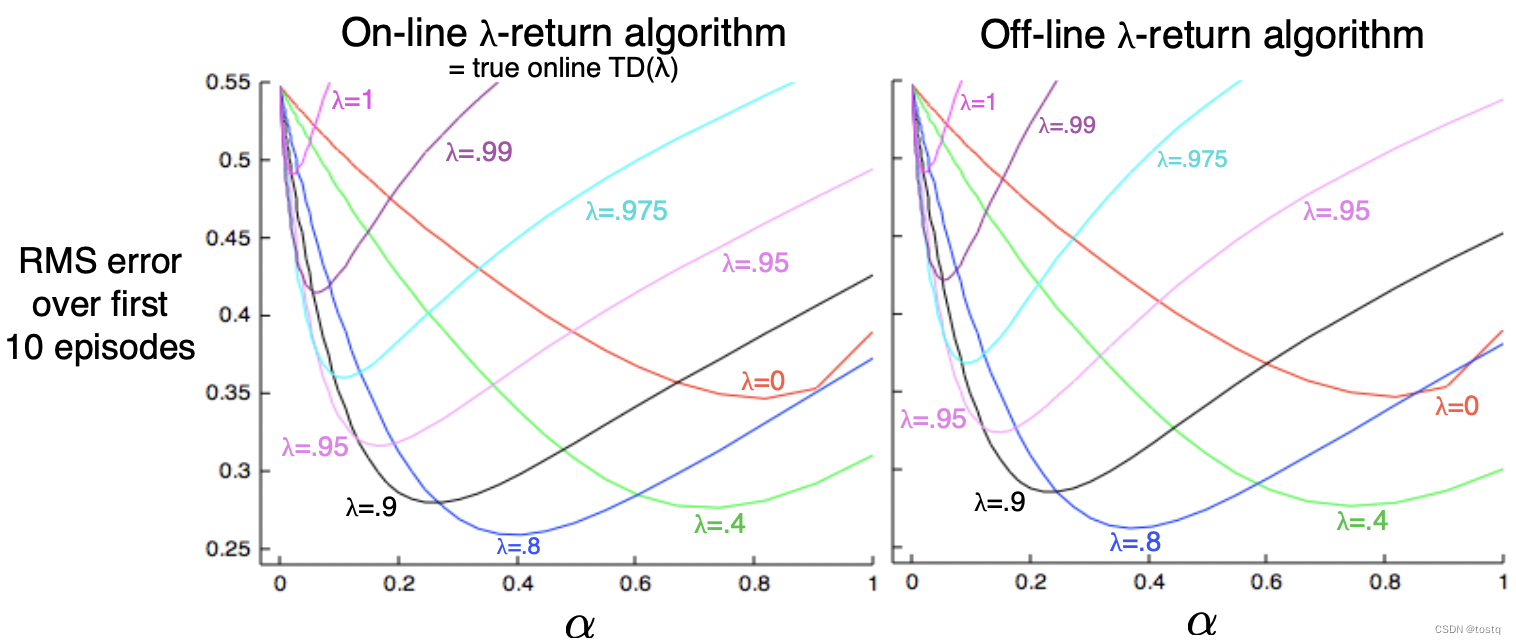
4. True Online TD(λ)