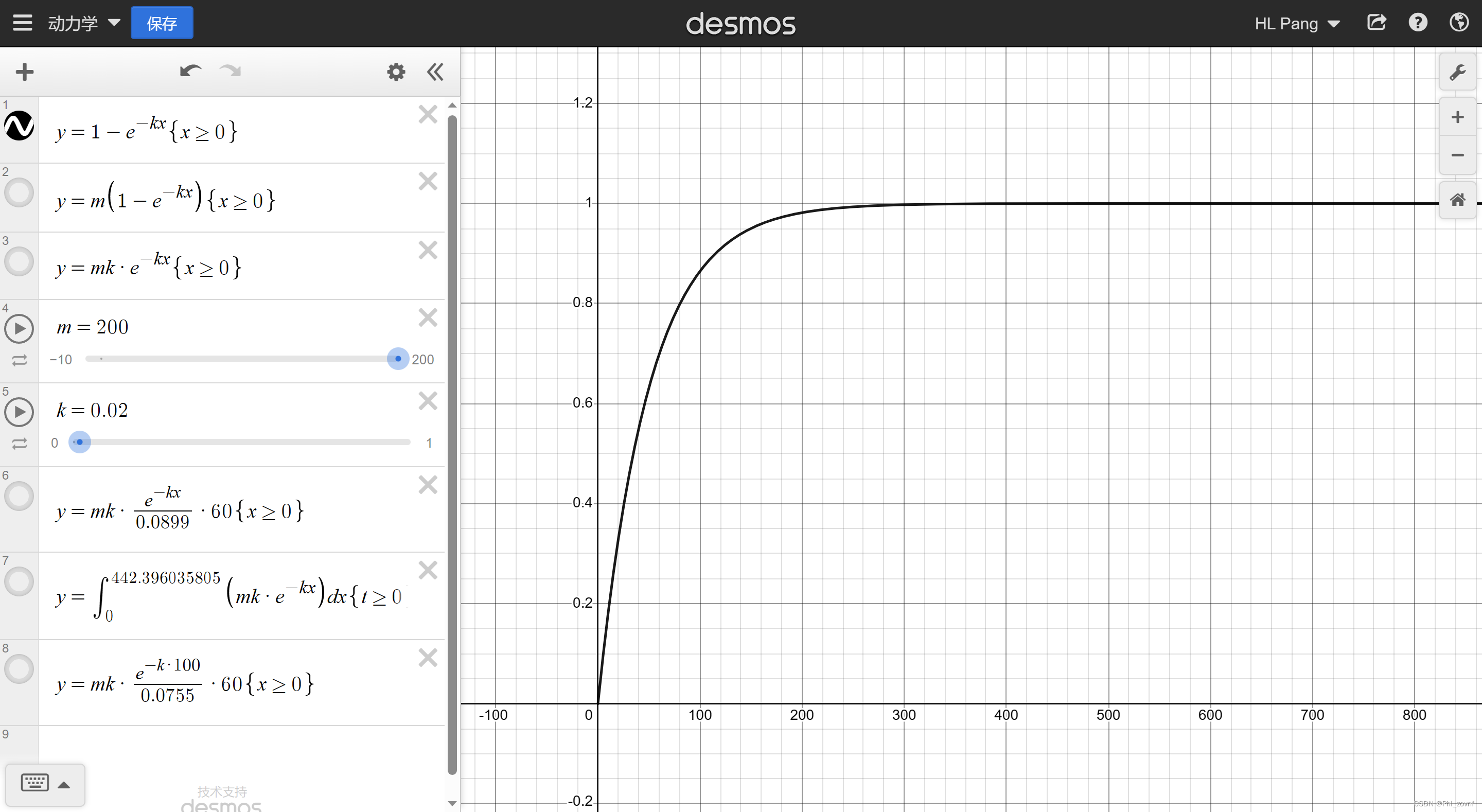
在经典的合金氢化物动力学描述中，有一种是用JMAK方程来描述和拟合合金的吸放氢过程，方程很简洁：，其中是反应程度或者百分比，表示合金氢化物吸氢或者放氢的程度，是该合金吸氢或放氢的一种特征常数，经常是通过实验测得动力学曲线后进行拟合得到，是时间。该方程的曲线形状如下图所示。

 

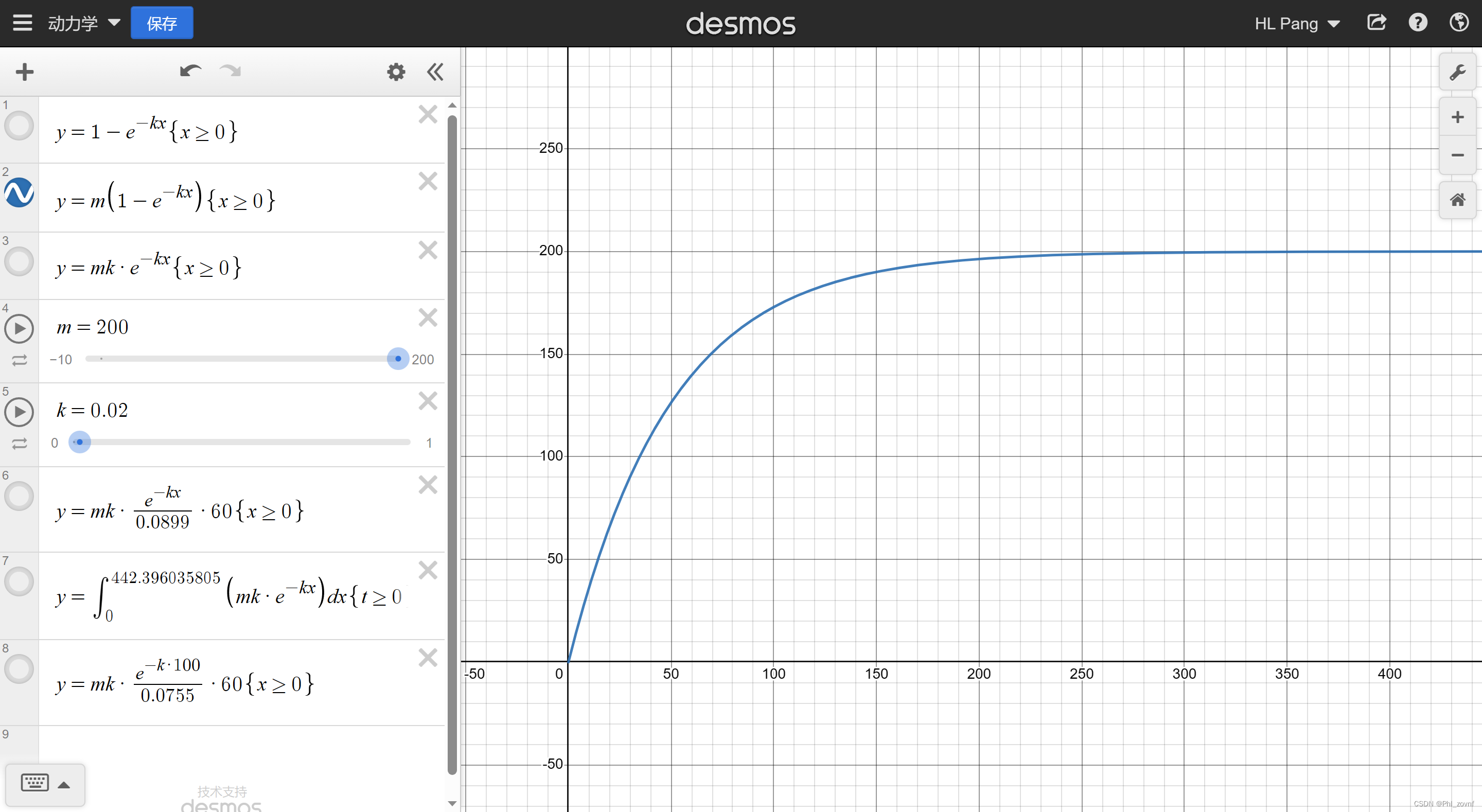
        由于 是反应程度，因此假设合金最终能放出千克的氢气，则方程可变为，该方程对时间进行求导，可得，该曲线即为瞬时质量流量曲线，其曲线形状如下图，越大，初始瞬时流量越大，放氢时间越短。实测可取值0.00005~0.05之间。

        合金放氢后，使得容器内压力上升，根据，是放氢总质量，在这里，我假设，利用，，，，设时间小量，可知，由此得

        参照之前《恒容容器放气的瞬时流量的计算》文章，链接如下。恒容容器放气的瞬时流量的计算https://blog.csdn.net/qq_24800941/article/details/130911222?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22130911222%22%2C%22source%22%3A%22qq_24800941%22%7D

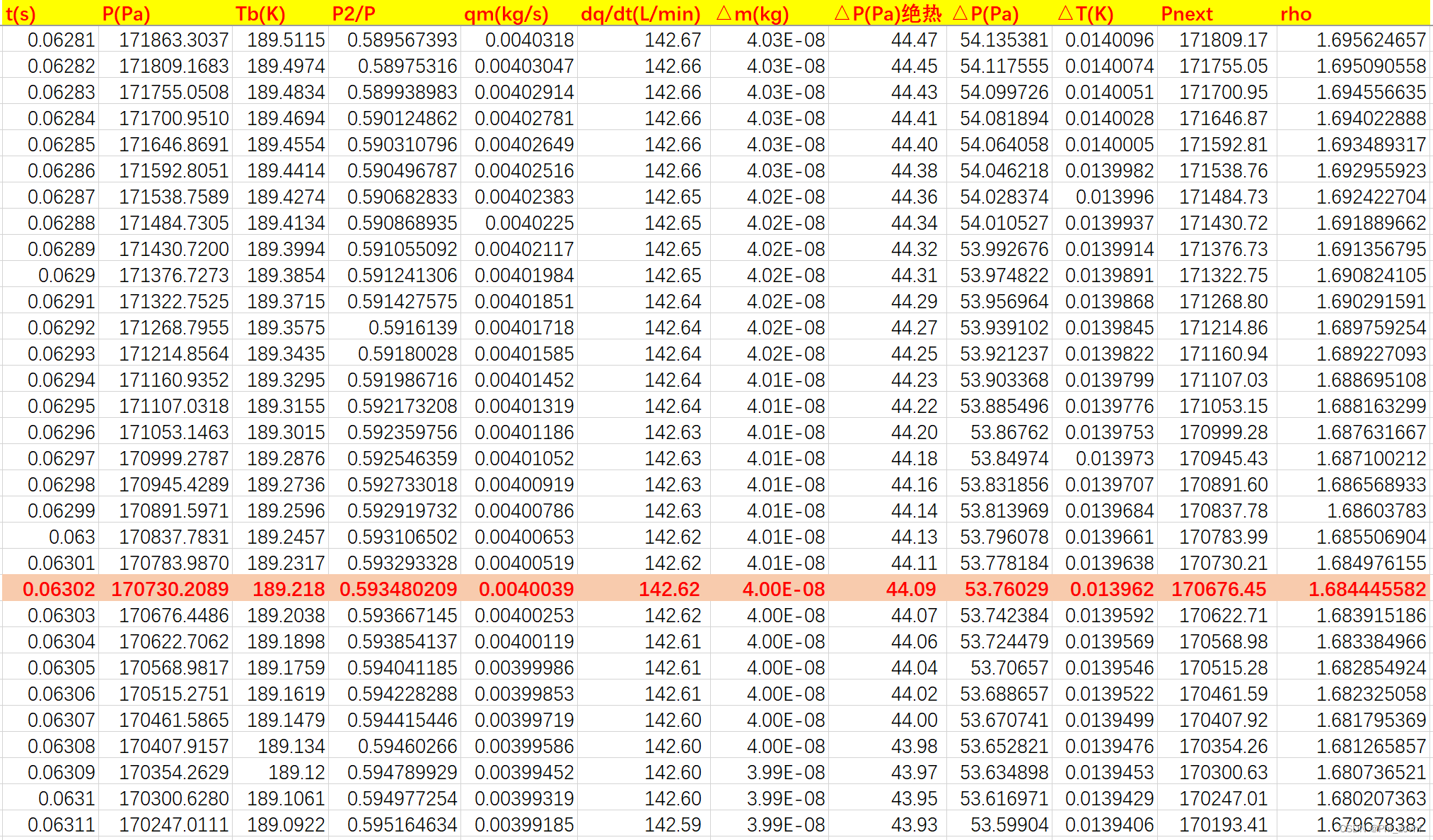
        根据第三种方法的数值计算结果，可以知道在非壅塞流状态下，大概0.063s时，容器内流失的质量或者压降才跟上述计算的结果在数量级上接近。        很多时候，我们在测量合金放氢量的时候，不是在平衡压力下放氢，而是使盛装合金的容器在一定的温度下，使其腔内压力人为控制在大于该温度平衡氢压之上一定的数值，如等。然后放气过程阀门全开，测量瞬时流量随时间的变化，此时不可避免就会遇到壅塞流和亚声速流的情况。根据上一篇文章中小孔放气模型的分析，排气到大气压的整个排气过程时间在左右，又根据，，得到放出的氢气质量占总质量储氢量的0.2%，可见占比是非常小的。同时，根据上一篇文章数值计算结果，不计合金放氢过程，放出的氢有。也就是说，这样在容器较小、合金储氢量比较大时的放氢的过程中，对合金整体的脱氢瞬时流量随时间变化的曲线影响不是很大。很多时候，流量计的记录数据的间隔为，因此，记录的曲线也近似认为就是合金的瞬时流量随时间变化的曲线。

        当然，笔者也很好奇，将合金释放的氢气代入到瞬时流量计算的公式里面，到底会发生什么？算出来的跟JMAK方程求导后得到瞬时流量随时间关系的曲线是否有很大出入？既然产生了问题，那就试试把数据代入方程中，算一算。

        首先回顾一下，算的方程组有哪些，这里用的是《恒容容器放气的瞬时流量的计算》中第二种方法，原因在于，笔者认为温度到最后会上升，不是单纯的绝热过程计算。

流量公式组：，合金公式组：

        由于要用数值求解法，因此在这里我先假设一个时间小量，并给出以下边界条件：初始压力，初始温度，初始，这是因为临界压力比为，比热比取，，，截面，合金方面，动力学中的，储氢总量。

         另外，合金一开始就放氢，使容器内压力上升，因此我每一步都让合金产生的压升直接加在当前压力那一列，即，首先计算当前时间的瞬时流量，利用，得到，利用得到，所以有，。数值计算结果如下图，仅列出部分值。注意，，是“rho”那一列数据。

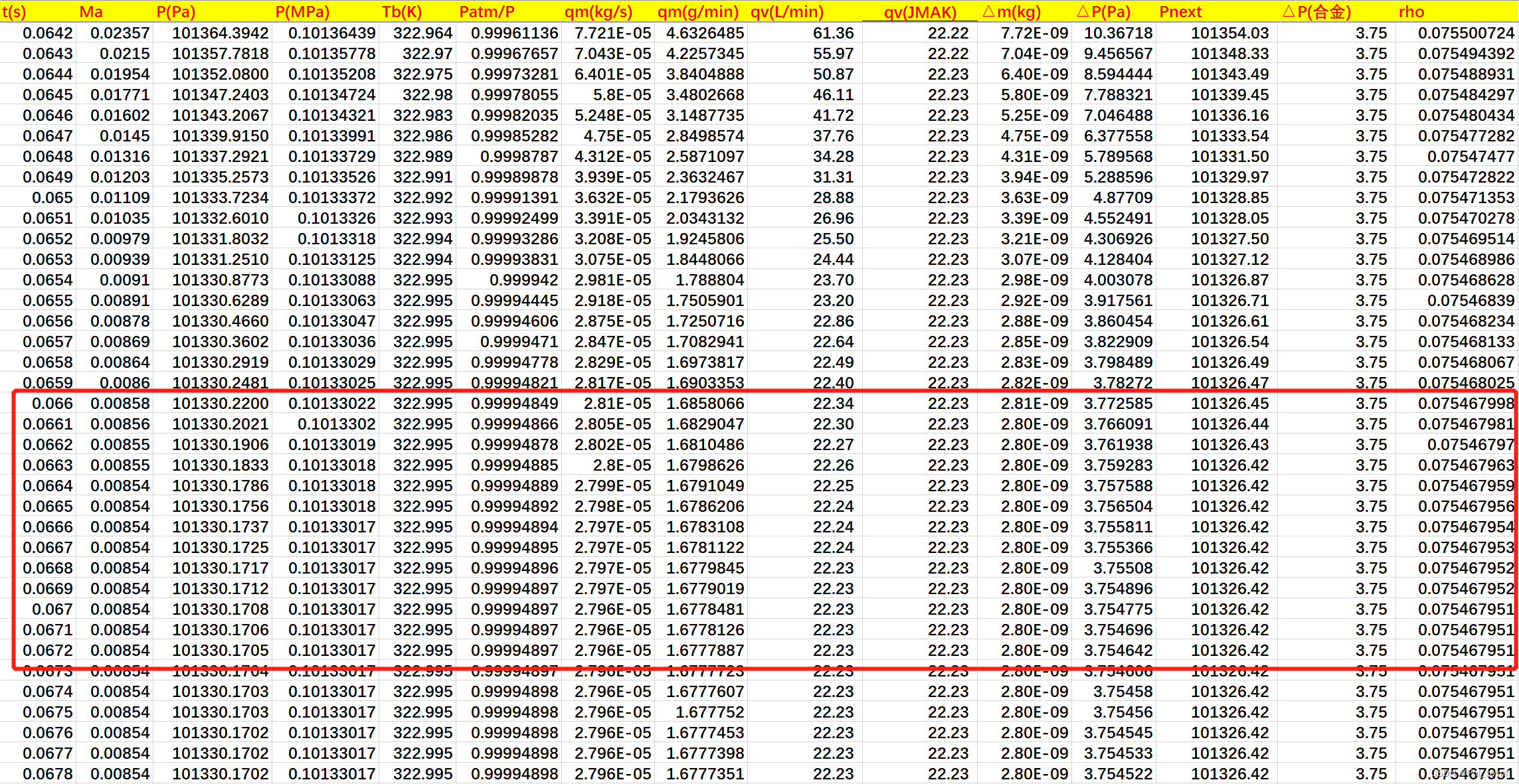
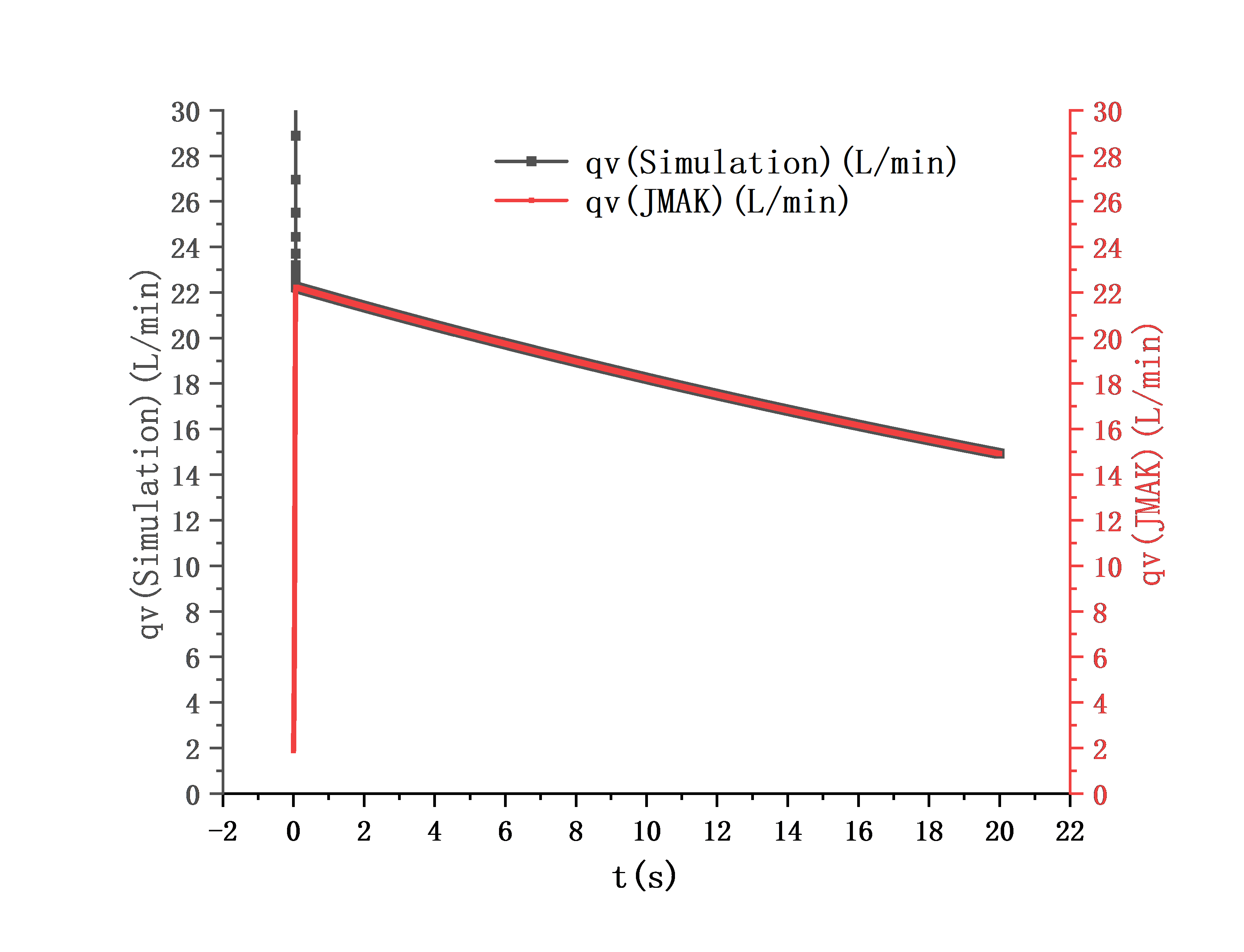
        从结果来看，数值计算的在基本快要降至时，瞬时流量值才与基本一致，笔者觉得挺神奇的，从的式子，可以看出压力当接近时，压力贡献项就基本只有合金的放氢过程了，相当于似乎在说，前面放气阶段，合金放氢过程可以忽略不计，完全是容器内非合金部分气体的快速放气过程，而且经过壅塞流和亚声速流状态。然后，接下来的阶段就是合金放氢过程为主导，瞬时流量基本就是JMAK方程解出的数值解。

        另外，很多时候，燃料电池不同功率下都会有一个氢气流速要求（如：1L/min等），合金储氢怎么去匹配这个氢气流速，这完全取决于合金的动力学性能。不过，对于不同的场景，不同的需求，合金会存储在不同的尺寸的罐子里面，加上材料本身的性质、热管理手段的不同、结构的不同，导致合金动力学性能曲线也会有所不一样。这时候，就要适当利用仿真软件进行模拟现实情况了，而且实测试验也会少不了，对数据进行合理的修正。当然，动力学方程不仅仅只有JMAK方程，还有很多数学模型来拟合，当中的学问深之又深，有种物理模型的尽头就是搞数学一样，跨学科的感觉就此而来。

结束语：感谢阅读至此，希望这篇文章对你有所启发和帮助，欢迎大佬私信交流。