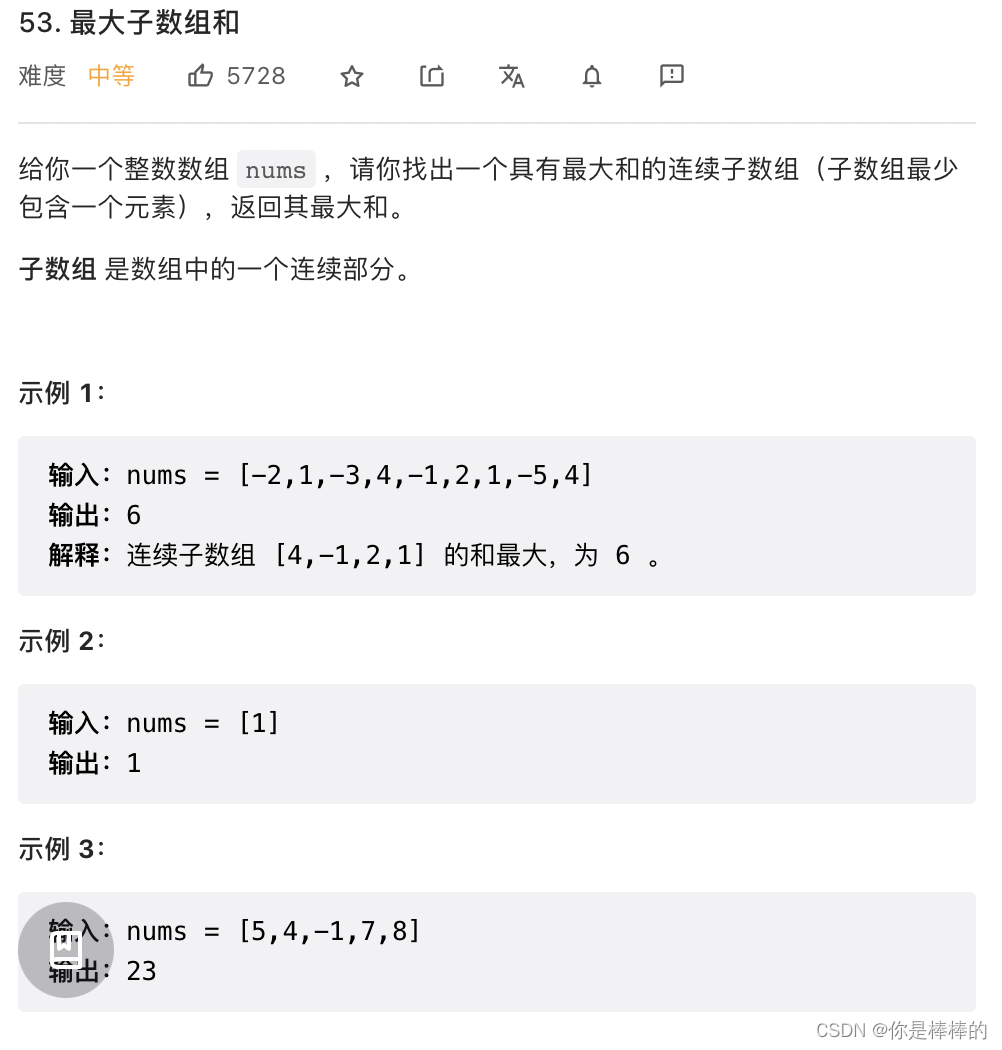
贪心算法

• 时间复杂度：代码中只有一个循环，循环次数为数组的长度，因此时间复杂度为 O(n)，其中 n 是数组的长度。
• 空间复杂度：代码中只使用了常数级别的额外空间，因此空间复杂度为 O(1)。

这段代码使用贪心算法的思想，通过遍历数组的过程中不断更新当前子数组的和，以获得最大的子数组和。

具体流程如下：

1. 定义变量 maxAns，用于记录最大子数组和的初始值，初始化为一个极小值。
2. 获取数组的长度，并定义变量 ans 用于存储当前子数组和的值，begin 用于记录当前子数组的起始位置，le 用于记录最大子数组和的起始位置，ri 用于记录最大子数组和的结束位置。
3. 遍历数组，从第一个元素开始。
4. 更新当前子数组和的值，累加当前元素到 ans。
5. 如果当前子数组和大于等于最大子数组和，则更新最大子数组和的值、起始位置和结束位置。
6. 如果当前子数组和小于0，则将当前子数组和

func main(){
	nums:=[]int{2,6,3,4,7}
	ans:=maxSubArray(nums)
	fmt.Println(ans)
}

func maxSubArray(nums []int) int {
	maxAns := -99999999999 // 定义变量 maxAns，用于存储最大子数组和的初始值，初始化为一个极小值

	m := len(nums) // 获取数组的长度
	ans := 0       // 定义变量 ans，用于存储当前子数组和的值
	begin := 0     // 定义变量 begin，表示当前子数组的起始位置
	le := 0        // 定义变量 le，用于记录最大子数组和的起始位置
	ri := m - 1    // 定义变量 ri，用于记录最大子数组和的结束位置

	for i := 0; i < m; i++ { // 遍历数组
		ans = ans + nums[i] // 更新当前子数组和的值

		if ans >= maxAns { // 如果当前子数组和大于等于最大子数组和
			maxAns = ans // 更新最大子数组和的值
			le = begin   // 更新最大子数组和的起始位置
			ri = i       // 更新最大子数组和的结束位置
		}

		if ans < 0 { // 如果当前子数组和小于0
			ans = 0       // 将当前子数组和重置为0
			begin = i + 1 // 更新子数组的起始位置为下一个元素的位置
		}
	}

	fmt.Println(maxAns, le, ri) // 打印最大子数组和、起始位置和结束位置
	return maxAns                // 返回最大子数组和的结果
}