一、Mathf
(一)Mathf 和 Math
Math 是 C# 中封装好的用于数学计算的工具类 —— 位于 System 命名空间中
Mathf 是 Unity 中封装好的用于数学计算的工具结构体 —— 位于 UnityEngine 命名空间中
他们都是提供来用于进行数学相关计算的
Mathf 和 Math 中的相关方法几乎一样
但 Mathf 是 Unity 专门封装的,不仅包含 Math 中的方法,还多了一些适用于游戏开发的方法
所以我们在进行 Unity 游戏开发时,使用 Mathf 中的方法用于数学计算即可
(二)常用方法
-
PI
print(Mathf.PI);
2.Abs - 取绝对值
print(Mathf.Abs(-10)); // 10
print(Mathf.Abs(-20)); // 20
print(Mathf.Abs(1)); // 1
3.CeilToInt - 向上取整
float f = 1.3f;
int i = (int)f;
print(i); // 1
print(Mathf.CeilToInt(f)); // 2
print(Mathf.CeilToInt(1.00001f)); // 2
4.FloorToInt - 向下取整
print(Mathf.FloorToInt(9.6f)); // 9
5.Clamp - 钳制函数
print(Mathf.Clamp(10, 11, 20)); // 11
print(Mathf.Clamp(21, 11, 20)); // 20
print(Mathf.Clamp(15, 11, 20)); // 15
6.Max / Min - 获取最大 / 小值
print(Mathf.Max(1, 2, 3, 4, 5, 6, 7, 8)); // 8
print(Mathf.Max(1, 2)); // 2
print(Mathf.Min(1, 2, 3, 4, 545, 6, 1123, 123)); // 1
print(Mathf.Min(1.1f, 0.4f)); // 0.4
7.Pow - 一个数的 n 次幂
print(Mathf.Pow(4, 2)); // 16
print(Mathf.Pow(2, 3)); // 8
8.RoundToInt - 四舍五入
print(Mathf.RoundToInt(1.3f)); // 1
print(Mathf.RoundToInt(1.5f)); // 2
9.Sqrt - 返回一个数的平方根
print(Mathf.Sqrt(4)); // 2
print(Mathf.Sqrt(16)); // 4
print(Mathf.Sqrt(64)); // 8
10.IsPowerOfTwo - 判断一个数是否是 2 的 n 次方
print(Mathf.IsPowerOfTwo(4)); // true
print(Mathf.IsPowerOfTwo(8)); // true
print(Mathf.IsPowerOfTwo(3)); // false
print(Mathf.IsPowerOfTwo(1)); // true
11.Sign - 判断正负数
print(Mathf.Sign(0)); // 0
print(Mathf.Sign(10)); // 1
print(Mathf.Sign(-10)); // -1
print(Mathf.Sign(3)); // 1
print(Mathf.Sign(-2)); // -1
(三)Lerp 方法
Lerp 函数公式:result = start + (end - start) * t
其中,t 为插值系数,取值范围为 0 ~ 1
函数调用:result = Mathf.Lerp(start, end, t);
// 插值运算用法一
// 每帧改变start的值——变化速度先快后慢,位置无限接近,但是不会得到end位置
start = Mathf.Lerp(start, 10, Time.deltaTime);
// 插值运算用法二
// 每帧改变t的值——变化速度匀速,位置每帧接近,当t>=1时,得到结果
time += Time.deltaTime;
result = Mathf.Lerp(start, 10, time);
应用:控制物体移动
public Transform B; // 目标物体位置
public float moveSpeed; // 移动速度
private Vector3 bNowPos; // B 当前的位置
private Vector3 pos; // 该物体的位置
private Vector3 startPos; // 每次运动的起始位置
private float time;
// 第一种 先快后慢的形式
pos = this.transform.position;
pos.x = Mathf.Lerp(pos.x, B.position.x, Time.deltaTime * moveSpeed);
pos.y = Mathf.Lerp(pos.y, B.position.y, Time.deltaTime * moveSpeed);
pos.z = Mathf.Lerp(pos.z, B.position.z, Time.deltaTime * moveSpeed);
this.transform.position = pos;
// 第二种 匀速运动
if (bNowPos != B.transform.position) {
time = 0;
bNowPos = B.transform.position;
startPos = transform.position;
}
time += Time.deltaTime;
pos.x = Mathf.Lerp(startPos.x, bNowPos.x, time);
pos.y = Mathf.Lerp(startPos.y, bNowPos.y, time);
pos.z = Mathf.Lerp(startPos.z, bNowPos.z, time);
transform.position = pos;
(四)三角函数
// 弧度转角度
float rad = 1;
float anger = rad * Mathf.Rad2Deg;
print(anger);
// 角度转弧度
anger = 1;
rad = anger * Mathf.Deg2Rad;
print(rad);
// 注意:Mathf中的三角函数相关函数,传入的参数需要时弧度值
print(Mathf.Sin(30 * Mathf.Deg2Rad)); // 0.5
print(Mathf.Cos(60 * Mathf.Deg2Rad)); // 0.5
// 注意:反三角函数得到的结果是 正弦或者余弦值对应的弧度
rad = Mathf.Asin(0.5f);
print(rad * Mathf.Rad2Deg);
rad = Mathf.Acos(0.5f);
print(rad * Mathf.Rad2Deg);
二、坐标系
(一)世界坐标系
原点:世界的中心点
轴向:世界坐标系的三个轴向是固定的
// 目前学习的和世界坐标系相关的
this.transform.position; // 坐标
this.transform.rotation; // 旋转角度
this.transform.eulerAngles; // 欧拉角度
this.transform.lossyScale; // 本地缩放大小
// 修改他们 会是相对世界坐标系的变化
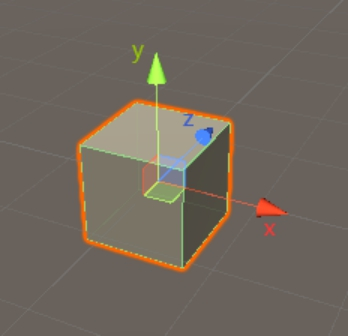
(二)物体坐标系
原点:物体的中心点(建模时决定)
轴向:
物体右方为 x 轴正方向
物体上方为 y 轴正方向
物体前方为 z 轴正方向
// 相对父对象的物体坐标系的位置 本地坐标 相对坐标
this.transform.localPosition;
this.transform.localEulerAngles;
this.transform.localRotation;
this.transform.localScale;
// 修改他们 会是相对父对象物体坐标系的变化
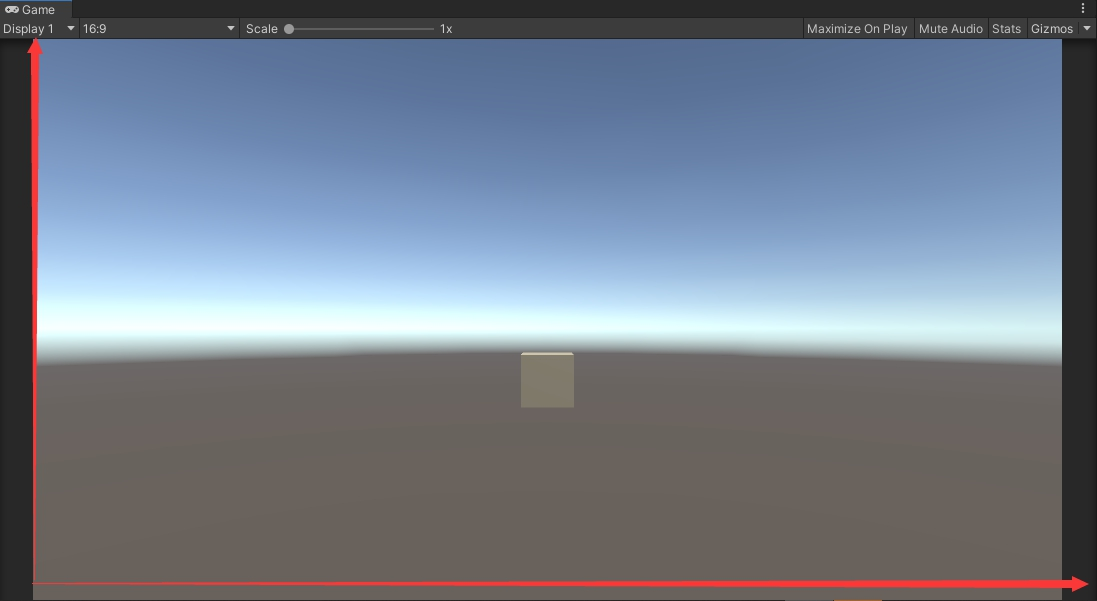
(三)屏幕坐标系
原点:屏幕左下角
轴向:
向右为 x 轴正方向
向上为 y 轴正方向
最大宽高:
Screen.width
Screen.height
Input.mousePosition; // 鼠标位置
Screen.width; // 屏幕宽
Screen.height; // 屏幕高
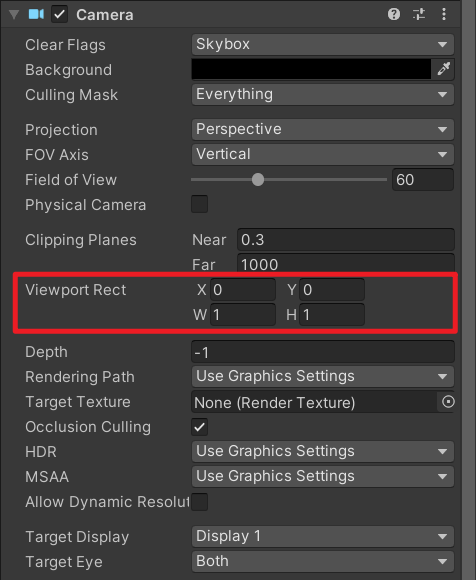
(四)视口坐标系
原点:屏幕左下角
轴向:
向右为 x 轴正方向
向上为 y 轴正方向
特点:
左下角为(0, 0)
右上角为(1, 1)
和屏幕坐标类似,将坐标单位化
(五)坐标转换
// 世界转本地
this.transform.InverseTransformDirection
this.transform.InverseTransformPoint
this.transform.InverseTransformVector
// 本地转世界
this.transform.TransformDirection
this.transform.TransformPoint
this.transform.TransformVector
// 世界转屏幕
Camera.main.WorldToScreenPoint
// 屏幕转世界
Camera.main.ScreenToWorldPoint
// 世界转视口
Camera.main.WorldToViewportPoint
// 视口转世界
Camera.main.ViewportToWorldPoint
// 视口转屏幕
Camera.main.ViewportToScreenPoint
// 屏幕转视口
Camera.main.ScreenToViewportPoint;
三、向量 Vector3
(一)向量模长和单位向量
// Vector3中提供了获取向量模长的成员属性
// magnitude
print(AB.magnitude);
Vector3 C = new Vector3(5, 6, 7);
print(C.magnitude);
print(Vector3.Distance(A, B));
// Vector3中提供了获取单位向量的成员属性
// normalized
print(AB.normalized);
print(AB / AB.magnitude);
(二)调试画线
// 画线段
// 前两个参数 分别是 起点 终点
Debug.DrawLine(this.transform.position, this.transform.position + this.transform.forward, Color.red);
// 画射线
// 前两个参数 分别是 起点 方向
Debug.DrawRay(this.transform.position, this.transform.forward, Color.white);
(三)向量点乘
public Transform target;
// 得到两个向量的点乘结果
// 向量 a 点乘 AB 的结果
float dotResult = Vector3.Dot(transform.forward, target.position - transform.position);
if (dotResult >= 0) print("它在我前方");
else print("它在我后方");
// 通过点乘推导公式算出夹角
// 1.用单位向量算出点乘结果
dotResult = Vector3.Dot(transform.forward, (target.position - transform.position).normalized);
// 2.用反三角函数得出角度
print(Mathf.Acos(dotResult) * Mathf.Rad2Deg);
// Vector3中提供了 得到两个向量之间夹角的方法
print(Vector3.Angle(transform.forward, target.position - transform.position));
(四)向量叉乘
// 假设向量 A和B 都在 XZ平面上
// 向量A 叉乘 向量 B
// y大于0 证明 B在A右侧
// y小于0 证明 B在A左侧
Vector3 C = Vector3.Cross(B.position, A.position);
if (C.y > 0) print("A在B的右侧");
else print("A在B的左侧");
(五)向量插值运算
-
线性插值
public Transform target; // 目标物体位置
public Transform A; // 先快后慢移动到 Target
public Transform B; // 匀速运动到 Target
private Vector3 nowTarget; // 当前 B 的位置
private Vector3 startPos; // 每次运行时 B 的起始位置
private float time;
// Start is called before the first frame update
private void Start() {
startPos = B.position;
}
// Update is called once per frame
private void Update() {
// result = start + (end - start) * t
// 1.先快后慢 每帧改变start位置 位置无限接近 但不会得到end位置
A.position = Vector3.Lerp(A.position, target.position, Time.deltaTime);
// 2.匀速 每帧改变时间 当t>=1时 得到结果
// 这种匀速移动 当time>=1时 我改变了 目标位置后 它会直接瞬移到我们的目标位置
if (nowTarget != target.position) {
nowTarget = target.position;
time = 0;
startPos = B.position;
}
time += Time.deltaTime;
B.position = Vector3.Lerp(startPos, nowTarget, time);
}
-
球形插值
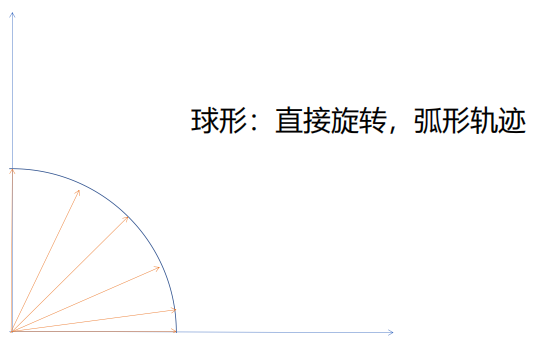
position = Vector3.Slerp(Vector3.right * 10, Vector3.left * 10 + Vector3.up * 0.1f, time * 0.01f);
四、四元数 Quaternion
(一)欧拉角
由三个角度 (x, y, z) 组成 ,在特定坐标系下用于描述物体的旋转量
空间中的任意旋转都可以分解成绕三个互相垂直轴的三个旋转角组成的序列
heading-pitch-bank 是一种最常用的旋转序列约定,即 Y - X - Z 约定
heading:物体绕自身的对象坐标系的 Y 轴,旋转的角度
pitch:物体绕自身的对象坐标系的 X 轴,旋转的角度
ban:物体绕自身的对象坐标系的 Z 轴,旋转的角度
Inspector 窗口中调节的 Rotation 就是欧拉角
this.transform.eulerAngles 得到的就是欧拉角角度
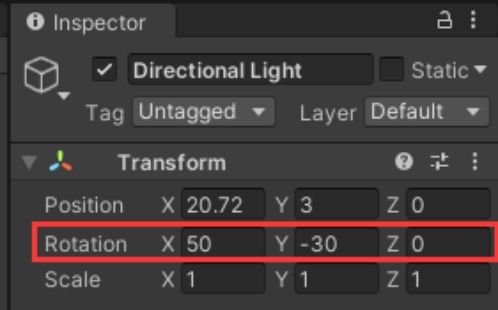

-
优点:
-
直观、易理解
-
存储空间小(三个数表示)
-
可以进行从一个方向到另一个方向旋转大于180度的角度
-
-
缺点:
-
同一旋转的表示不唯一
例如,Rotation(x, y, z) = Rotation(x + 360, y + 360, z + 360)
-
万向节死锁
-
(二)万向节死锁
万向节死锁的意义就是在 X 轴转 90度的情况下,后面左乘 Z(绕基坐标下 Z)与右乘 Y(绕自身 Y,实际与基坐标 Z 一样了)实际效果是相同的,丧失了自由度。
例如,在 Unity 中,将 Rotation 中的 X 设置为 90,之后调节 Y 和调节 Z 的大小,物体的转动都会是沿一个角度的。
(三)四元数简介
四元数是简单的超复数,由实数加上三个虚数单位组成 主要用于在三维空间中表示旋转
四元数原理包含大量数学相关知识,较为复杂,比如:复数、四维空间等等
因此此处我们只对其基本构成和基本公式进行讲解,如想深入了解数学原理请从数学层面去查找资料了解它
-
四元数的构成
一个四元数包含一个标量和一个 3D 向量
[w, v],w为标量,v为 3D 向量,即[w, (x, y, z)]
对于给定的任意一个四元数: 表示 3D 空间中的一个旋转量
-
轴角对
在 3D 空间中,任意旋转都可以表示绕着某个轴旋转一个旋转角得到
对于给定旋转,假设为绕着 n 轴,旋转 β 度,n 轴为 (x, y, z)
那么可以构成四元数为
四元数 Q = [cos(β / 2), n · sin(β / 2)]
四元数 Q = [cos(β / 2), x · sin(β / 2), y · sin(β / 2), z · sin(β / 2)]
四元数 Q 则表示绕着轴 n,旋转 β 度的旋转量
-
Unity 中的 Quaternion
Quaternion 是 Unity 中表示四元数的结构体
// 轴角对公式初始化
// 四元数 Q = [cos(β/2), sin(β/2)x, sin(β/2)y, sin(β/2)z]
Quaternion q = new Quaternion(sin(β/2)x, sin(β/2)y, sin(β/2)z, cos(β/2));
// 轴角对方法初始化
// 四元数Q = Quaternion.AngleAxis(角度, 轴);
Quaternion q = Quaternion.AngleAxis(60, Vector3.right);
3.四元数和欧拉角转换
// 1.欧拉角转四元数
Quaternion q2 = Quaternion.Euler(60, 0, 0);
// 2.四元数转欧拉角
print(q2.eulerAngles);
(四)常用方法
-
单位四元数
单位四元数表示没有旋转量(角位移)
当角度为 0 或者 360 度时,对于给定轴都会得到单位四元数
[1, (0, 0, 0)]和[-1, (0, 0, 0)] 都是单位四元数,表示没有旋转量
// 单位四元数
print(Quaternion.identity);
2.插值运算
四元数中同样提供如同 Vector3 的插值运算:Lerp 和 Slerp
在四元数中 Lerp 和 Slerp 只有一些细微差别,由于算法不同,Slerp 的效果会好一些
Lerp 的效果相比 Slerp 更快但是如果旋转范围较大效果较差,所以建议使用 Slerp 进行插值运算
public Transform target;
public Transform A;
public Transform B;
private Quaternion start;
private float time;
start = B.transform.rotation;
// 无限接近 先快后慢
A.transform.rotation = Quaternion.Slerp(A.transform.rotation, target.rotation, Time.deltaTime);
// 匀速变化 time>=1 到达目标
time += Time.deltaTime;
B.transform.rotation = Quaternion.Slerp(start, target.rotation, time);
3.方向转四元数
Quaternino.LookRotation(面朝向量);
LookRoataion 方法可以将传入的面朝向量转换为对应的四元数角度信息
当人物面朝向想要改变时,只需要把目标面朝向传入该函数,便可以得到目标四元数角度信息,之后将人物四元数角度信息改为得到的信息即可达到转向
Quaternion q = Quaternion.LookRotation(lookB.position - lookA.position);
lookA.rotation = q;
(五)实现缓慢看向目标
public Transform target;
private float roundTime;
public float roundSpeed;
private Quaternion startQ;
private Quaternion targetQ;
// 用目标的位置 减去 摄像机的位置 得到新的面朝向向量
targetQ = Quaternion.LookRotation(target.position - this.transform.position);
//先快后慢
this.transform.rotation = Quaternion.Slerp(this.transform.rotation, targetQ, Time.deltaTime* roundSpeed);
//匀速旋转
if (targetQ != Quaternion.LookRotation(target.position - transform.position)) {
targetQ = Quaternion.LookRotation(target.position - transform.position);
roundTime = 0;
startQ = transform.rotation;
}
roundTime += Time.deltaTime;
transform.rotation = Quaternion.Slerp(startQ, targetQ, roundTime * roundSpeed);
(六)四元数计算
-
四元数乘四元数
q3 = q1 * q2
两个四元数相乘得到一个新的四元数,代表两个旋转量的叠加,相当于旋转
注意:旋转相对的坐标系是物体自身坐标系
Quaternion q = Quaternion.AngleAxis(20, Vector3.up);
transform.rotation *= q;
2.四元数乘向量
v2 = q1 * v1(顺序不能反)
四元数乘向量返回一个新向量,可以将指定向量旋转对应四元数的旋转量,相当于旋转向量
Vector3 v = Vector3.forward;
print(v);
v = Quaternion.AngleAxis(45, Vector3.up) * v;
print(v);



![P20[6-8]编码器接口测速(软)](https://img-blog.csdnimg.cn/cdbc282958814c96b525b91941eed2fe.png)