本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。

系统码的编译码

线性分组码的编码器

1. 如图硬件实现。生成矩阵为

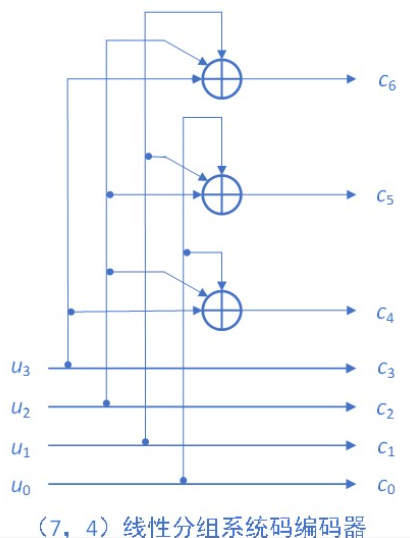
$$G=\left[\begin{array}{l}1011000\\ 1110100\\ 1100010\\ 0110001\end{array}\right]$$

2. 查表。(软件)

3. 矩阵乘法。(软件)

线性分组码的译码器

所有编码符合监督方程, 监督方程在译码中非常重要。

对二元信道, 传输后 $\mathbf{y}=\mathbf{C}+\mathbf{e}$ , 向量 $\mathrm{e}=\left[e_{n-1},e_{n-2},\dots ,e_i,\dots ,e_0\right]$ 称为错误图样。 $e_i=1$ 表示第 i 位错误。

如果译码器能推测出错误图样e, 那它就可以给出译码结果为
$$\hat{\mathbf{C}}=\mathbf{y}+\mathbf{e}$$

伴随式校验(Syndrome Testing)

设 $\mathbf{y}=\left[y_{n-1}{y}_{n-2}\cdots y_0\right]$ 是一个接收矢量,由传输的$\mathbf{C}=\left[c_{n-1}{c}_{n-2}\cdots c_0\right]$产生。可以将 $\mathbf{y}$ 写成$\mathbf{y}=\mathbf{C}+\mathbf{e}$

其中 $\mathrm{e}=\left[e_{n-1},e_{n-2},\dots ,e_i,\dots ,e_0\right]$ 是由信道引入的错误矢量（图样）。

在 $2^n$ 个 $\mathrm{n}$ 元组空间中存在 $2^n-1$ 个非零的潜在错误图样。（为什么?）

$\mathbf{y}$ 的伴随式 (或称校正子) 定义为

$\mathbf{S}={\mathbf{yH}}^{\mathbf{T}}$

• 若 $\mathbf{S}=0,\mathbf{y}$ 是有效码字.

• 若 $ \mathbf{y}$ 包含可检测到的错误，伴随式 $\mathbf{S}\ne 0$ ;

• 若 $ \mathbf{y}$ 包含可以纠正的错误, $\mathbf{S}$ 将由特殊的非零值来指示特定的错误图样。

  线性分组码的一个重要性质是,（可纠正的）错误图样与伴随式一一对应。

$$\mathbf{S}={\mathbf{yH}}^{\mathrm{T}}=(\mathbf{C}+\mathrm{e}){\mathbf{H}}^{\mathrm{T}}={\mathbf{CH}}^{\mathrm{T}}+{\mathrm{eH}}^{\mathrm{T}}={\mathrm{eH}}^{\mathrm{T}}$$

(7,4) 循环码校验矩阵如下所示, 设发送码字为 $\mathbf{C}=1000011$ , 接收矢量为 $\mathbf{y}=1100011$
试求伴随式矢量 $\mathbf{S}={\mathbf{yH}}^{\mathrm{T}}$ 并证明它等于 $ \mathrm{eH}^{\mathrm{T}}$

校验矩阵: $H=\left(\begin{array}{lllllll}0 & 1 & 1 & 1 & 1 & 0 & 0 \ 1 & 1 & 0 & 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 0 & 1\end{array}\right) $

注意:监督矩阵必须具有两个性质:

1. H中没有全0列，否则的话，相应码字位置上的错误就无法影响伴随式，因而无法检测。
2. H中的所有列是唯一的，如果H有两列相同，那么对应这两列发生的错码位置将无法识别。

例：已知 (7,3) 线性分组码的监督矩阵为
$$\mathbf{H}=\left(\begin{array}{lllllll}1& 0& 1& 1& 0& 0& 0\\ 1& 1& 1& 0& 1& 0& 0\\ 1& 1& 0& 0& 0& 1& 0\\ 0& 1& 1& 0& 0& 0& 1\end{array}\right)$$
信道输出端的接收矢量为
$$\mathbf{y}=\left(\begin{array}{lllllll}1& 0& 0& 1& 0& 0& 1\end{array}\right)$$
请求出 $\mathbf{y}$ 的伴随式。并估计最有可能的译码结果。

解: $\mathbf{S}=\mathbf{y}{\mathbf{H}}^T=\left(\begin{array}{llll}0& 1& 1& 1\end{array}\right)$
所有可能的错误图样有（1001001）（1010100) (1110011) (0000111) (0011010) (0100000) (0111101)
取码重最小即可能性最大的错误图样 (0100000) 为可纠正的错误图样。译码结果
$$\begin{array}{l}\hat{\mathbf{C}}=\mathbf{y}+{\mathbf{e}}^{\prime }=\left(\begin{array}{lllllll}1& 0& 0& 1& 0& 0& 1\end{array}\right)+\\ \left(\begin{array}{lllllll}0& 1& 0& 0& 0& 0& 0\end{array}\right)=\left(\begin{array}{lllllll}1& 1& 0& 1& 0& 0& 1\end{array}\right)\end{array}$$

纠错

伴随式不仅可以检测错误, 而且可以同时纠正错误, 因 为可纠正的错误图样与伴随式之间一一对应。

在硬判决译码中, 一般采用标准阵(standard array) 来完成纠错的设计。

标准阵包含了 $2^{\mathrm{n}}$ 个所有的可能接收矢量. 其第一行以全 0 码 字开始，包括了所有码字, 而第一列包括了所有可纠正的错误图样 (一般选汉明重量最小的元素)。每行称为一个陪集 (coset), 由第一列的错误图样 (称为陪集首)及其干扰的码字组成。 $(\mathbf{n}.\mathbf{k})$ 码的标准阵如下:

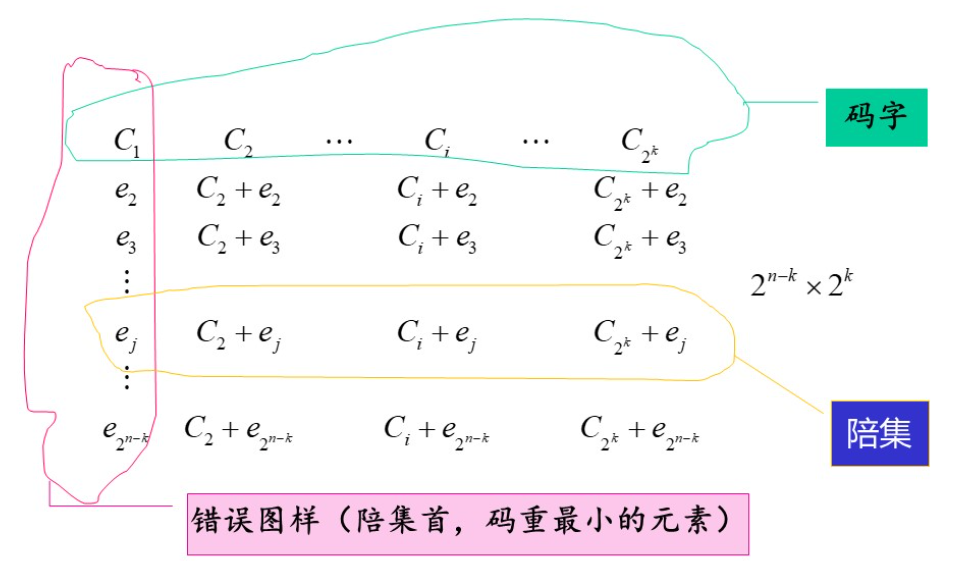
注意：码字 $C_1$ （全0码）起两个作用：既是其中的一个码字, 也是错误图样 ${\mathrm{e}}_1$ ,代表没有错误, 即 $\mathbf{y}=\mathbf{C}$ .

译码机制要求将每个有错的矢量用此矢量同列的最顶端的有效码字代替。

假设一个码字 ${\mathrm{C}}_{\mathrm{i}}$ 通过一个噪声信道, 接收矢量为量将被正确译码为码字 ${\mathrm{C}}_{\mathrm{i}}$ 。 如果错误图样不是一个陪集首, 那么将会导致译码错误。

陪集的伴随式

陪集中的每一个元素具有相同的伴随式。伴随式用于估计错误图样。

纠错译码

1. 计算 $\mathbf{y}$ 的伴随式 $\mathbf{S}={\mathbf{yH}}^{\mathrm{T}}$ .
2. 定位错误图样 (陪集首) ${\mathrm{e}}_{\mathrm{j}}$ , 它的伴随式与 ${\mathrm{yH}}^{\mathrm{T}}$ 相等。
3. 假设错误图样是由信道衰落引起的。
4. 错误接收的矢量或码字表示为 $\mathrm{C}=\mathbf{y}+{\mathrm{e}}_{\mathbf{j}}$ 。通过减去其中已识别出的错误来恢复正确码字。

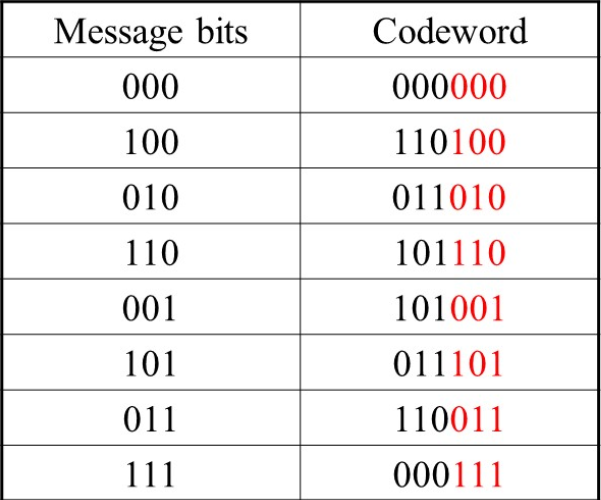
Example: (6,3)线性分组码如下表所示，求它的生成矩阵和监督矩阵。

其生成矩阵为
$$G=\left[\begin{array}{l}110100\\ 011010\\ 101001\end{array}\right]$$
监督矩阵为

$$H=\left[\begin{array}{l}100101\\ 010110\\ 001011\end{array}\right]$$
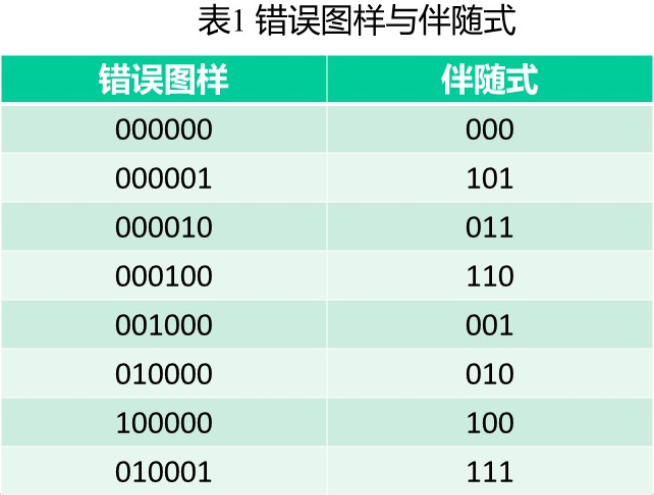
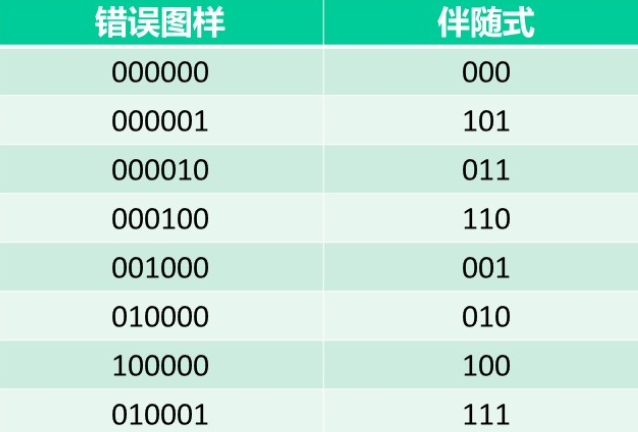
(6,3)码的标准阵如下。

根据标准阵，可以得到错误图样与伴随式的一一对应关系，可用来译码，同时完成纠错。

在线性分组码中，[全0码]码字一定是有效码字。

已知接收矢量y=001110.请问译码器译码所得是什么?

S = 100，监督矩阵为
$$H=\left[\begin{array}{l}100101\\ 010110\\ 001011\end{array}\right]$$
S=100

C=101110

U=110

译码方法与译码电路

(1) 在设计阶段:

对每一种可能伴随式的取值确定出它所对应的可纠正错误图样，存储为表格。

(2）译码器运行时:

当接收端收到y后，计算伴随式S，用S查可纠正错误图样表，根据查表结果纠正错误。

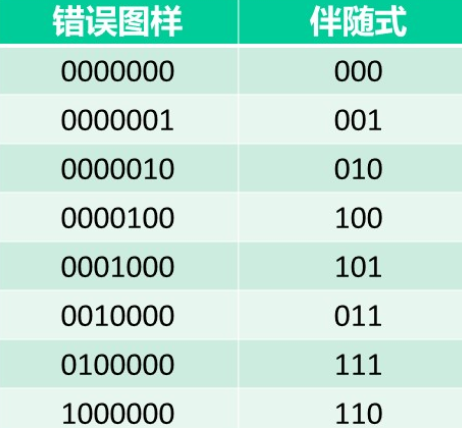
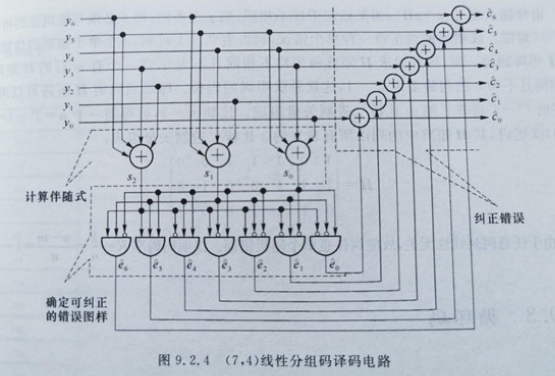
“查错误图样表”这个环节往往可以进行逻辑化简，比如在(7.4)码的情形下，“查错误图样表”是用3比特地址查8种结果，所有结果除全0外，只有1个1。这样的电路类似38译码器。

(7,4）码错误图样与伴随式表

汉明码

一能纠正单个随机错误、编码效率最高的线性分组码

• 主要参数：码长 $n=2^m-1$ ;
• 信息位： $k=n-m=2^m-1-m$ ;
• 监督位: $n-k=m$ , 且 $m\ge 3;(m=3,n=7,k=4)$
• 最小距离 : $d_{\text{min }}=d_0=3$
• 汉明码的非全 0 伴随式有 $n=2^{n-k}-1$ 个, 每个伴随式对应一种单比特错误图样, 因此每个伴随式就是监督矩阵 $\mathbf{H}$ 的一个列, 而 $\mathbf{H}$ 的所有列构成了全 0 以外的所有可能的 $n-k$ 比特向量。

如 m=3 , 则可以得到一个 $n=2^3-1=7$ 的 (7,4) 汉明码, 其 $\mathbf{H}$ 矩阵的列由所有非 0 三重组成:
$$H=\left(\begin{array}{lllllll}1& 0& 1& 1& 1& 0& 0\\ 1& 1& 1& 0& 0& 1& 0\\ 0& 1& 1& 1& 0& 0& 1\end{array}\right)$$
由于任意两列线性无关 (d=3, t=1) , 故能纠任意单个随机错误（监督矩阵的特性 d ）。 $R=k/n=1-m/n$ .

高效率纠错码。广泛应用于RAM中。

总结

线性分组码

①编码:生成矩阵编码

②译码:校验矩阵，错误图样，伴随式译码，标准阵

③生成矩阵与监督矩阵的关系

④汉明码

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.