名人说:一花独放不是春,百花齐放花满园。——《增广贤文》
作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊)目录
- 〇、Dijkstra迪杰斯特拉算法介绍
- 1、Dijkstra算法是什么?
- 2、Dijkstra算法的由来
- 3、Dijkstra算法的基本思想
- 一、代码及注释
- 二、思路阐明
- 三、样例测试
以下代码个人分享出来,仅供学习交流,且仅在CSDN平台发布,未经授权禁止二次转发。
〇、Dijkstra迪杰斯特拉算法介绍
1、Dijkstra算法是什么?
Dijkstra算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法,常规迪杰斯特拉算法的时间复杂度 O (n^2) 。
2、Dijkstra算法的由来
它是由荷兰计算机科学家艾茲赫尔·戴克斯特拉在1956年发现的,并于3年后在期刊上发表。

他的一些学术贡献包括(但不仅限于):
- 提出了目前在离散数学中应用广泛的最短路径算法(Dijkstra’s Shortest Path First Algorithm)
- 为解决操作系统中资源分配问题,提出银行家算法。
又是膜拜大佬的一天
3、Dijkstra算法的基本思想
- 首先,将所有的顶点分为两个集合:已经求出最短路径的顶点集合(用S表示)和未求出最短路径的顶点集合(用Q表示)。
- 初始时,S只包含源点,Q包含除源点外的其他顶点,源点到自身的距离为0,源点到其他顶点的距离为无穷大(或者是邻接矩阵中对应的权值)。
- 然后,每次从Q中选择一个距离最小的顶点u,将其加入到S中,并用u更新Q中的其他顶点的距离,即如果存在一条从u到v的边,且dist[u]+w(u,v)<dist[v],则更新dist[v]=dist[u]+w(u,v)。
- 重复上述过程,直到Q为空或者目标顶点被加入到S中。
- 最后,输出源点到其他顶点的最短距离和最短路径。
Dijkstra算法可以用不同的数据结构来实现,例如数组、堆、优先队列等。不同的数据结构会影响算法的时间复杂度和空间复杂度。一般来说,使用邻接表和优先队列可以达到较好的效率。本文以优先队列为例。
一、代码及注释
//创作者:Code_流苏(CSDN)
#include<iostream>
#include<vector>
#include<queue>
#include<string>
#define MAXV 100
#define INF 32767
using namespace std;
typedef struct
{
int no;
string name;
}VertexType;
typedef struct
{
int v;//边的终止顶点
int w;//边的权值
}Edge;
typedef struct//图的结构体
{
VertexType vex[MAXV];//顶点表
vector<Edge> arcs[MAXV];//邻接表
int vexnum,arcnum;//顶点数目和边的数目
}AMGraph;
void CreateGraph(AMGraph *G)//创建图
{
int i;
int u,v,w;
cout<<"请输入顶点数和边数: ";
cin>>G->vexnum>>G->arcnum;
cout<<"依次输入顶点名字: ";
for(i=0;i<G->vexnum;i++)
{
cin>>G->vex[i].name;
getchar();
}
cout<<"下标从0开始\n";
for(i=0;i<G->arcnum;i++)
{
G->vex[i].no=i;
cout<<"请输入第"<<i+1<<"条边<vi,vj>两个顶点和权值: ";
cin>>u>>v>>w;
G->arcs[u].push_back({v,w}); //添加边到邻接表
G->arcs[v].push_back({u,w}); //无向图需要添加两次
}
}
void Dispath(AMGraph G,int dist[],int path[],int s[],int v)//输出
{
int i,j,k;
int apath[MAXV],d;//存放一条最短路径及其顶点个数
for(i=0;i<G.arcnum;i++)//从顶点v到顶点i的路径
if(s[i]==1&&i!=v)
{
cout<<"从顶点"<<G.vex[v].name<<"到"<<G.vex[i].name<<"的路径长度为:"<<dist[i]<<"\t路径为:";
d=0;apath[d]=i;//添加路径上的终点
k=path[i];
if(k==-1)
cout<<"无路径\n";
else
{
while(k!=v)
{
d++;apath[d]=k;
k=path[k];
}
d++;apath[d]=v;//添加路径上的起点
cout<<G.vex[apath[d]].name;//输出起点
for(j=d-1;j>=0;j--)//输出其他顶点
cout<<","<<G.vex[apath[j]].name;
cout<<"\n";
}
}
}
void Dijkstra(AMGraph G,int v)//迪杰斯特拉算法
{
int dist[MAXV],path[MAXV];//path[]记录到达终点前的最后一个顶点
int s[MAXV];//0表示未加入最短路径顶点集,1已加入
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q; //优先队列,按照距离从小到大排序
int i,u;
for(i=0;i<G.vexnum;i++)//dist和path数组初始化
{
dist[i]=INF;//距离初始化为无穷大
s[i]=0;//s[]置空
path[i]=-1;//路径初始化为-1
}
dist[v]=0;//源点到自身的距离为0
q.push({0,v});//源点入队
while(!q.empty())//队列不为空时循环
{
u=q.top().second;//取出队首的顶点
q.pop();//出队
if(s[u]==1) continue;//如果已经加入最短路径顶点集,跳过
s[u]=1;//否则,将其加入最短路径顶点集
for(auto e:G.arcs[u])//遍历u的邻接边
if(s[e.v]==0)//如果终点不在s中
if(dist[u]+e.w<dist[e.v])//如果可以更新距离
{
dist[e.v]=dist[u]+e.w;//更新距离
path[e.v]=u;//更新路径
q.push({dist[e.v],e.v});//将终点入队
}
}
Dispath(G,dist,path,s,v);//输出
}
int main()
{
AMGraph G;
CreateGraph(&G);
Dijkstra(G,0);
return 0;
}
二、思路阐明
① 首先,创建一个图的结构体,用顶点表和邻接表来存储图的信息,顶点表中存储顶点的编号和名字,邻接表中存储每个顶点的邻接边和权值。
② 然后,输入顶点数和边数,以及每个顶点的名字和每条边的起点、终点和权值,将它们添加到图的结构体中。
③ 接着,定义一个dist数组,用来存储源点到其他顶点的最短距离,初始化为无穷大;定义一个path数组,用来存储到达终点前的最后一个顶点,初始化为-1;定义一个s数组,用来标记是否加入最短路径顶点集,初始化为0;定义一个优先队列,用来存储未加入最短路径顶点集的顶点,并按照距离从小到大排序。
④ 然后,将源点到自身的距离设为0,并将源点入队。
⑤ 接着,循环直到队列为空,每次取出队首的顶点u,并将其加入最短路径顶点集。然后遍历u的邻接边,如果终点v不在最短路径顶点集中,并且dist[u]+w<dist[v],则更新dist[v]为dist[u]+w,并更新path[v]为u,并将v入队。
⑥ 最后,输出源点到其他顶点的最短路径长度和路径。
三、样例测试
0- 4,依次代表A、B、C、D、E
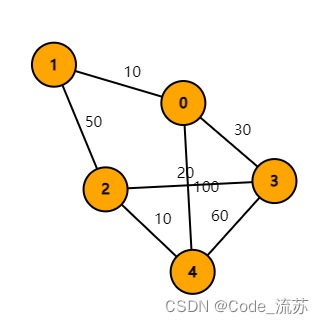
请输入顶点数和边数: 5 7
依次输入顶点名字: A B C D E
下标从0开始
请输入第1条边<vi,vj>两个顶点和权值: 0 1 10
请输入第2条边<vi,vj>两个顶点和权值: 0 3 30
请输入第3条边<vi,vj>两个顶点和权值: 0 4 100
请输入第4条边<vi,vj>两个顶点和权值: 1 2 50
请输入第5条边<vi,vj>两个顶点和权值: 2 4 10
请输入第6条边<vi,vj>两个顶点和权值: 3 2 20
请输入第7条边<vi,vj>两个顶点和权值: 3 4 60
从顶点A到B的路径长度为:10 路径为:A,B
从顶点A到C的路径长度为:50 路径为:A,D,C
从顶点A到D的路径长度为:30 路径为:A,D
从顶点A到E的路径长度为:60 路径为:A,D,C,E
--------------------------------
Process exited after 38.41 seconds with return value 0
请按任意键继续. . .
Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊)
如果对大家有帮助的话,希望大家能多多点赞+关注!这样我动力会更足哦! ღ( ´・ᴗ・` )比心